Capitolo 7 (ultimo aggiornamento 27/05/04)
7.1 Parametri di servizio di una linea elettrica
Una linea elettrica può essere classificata in base al numero dei conduttori,
reciprocamente isolati ( fili, funi, cavi, sbarre etc.), di cui è composta; le linee
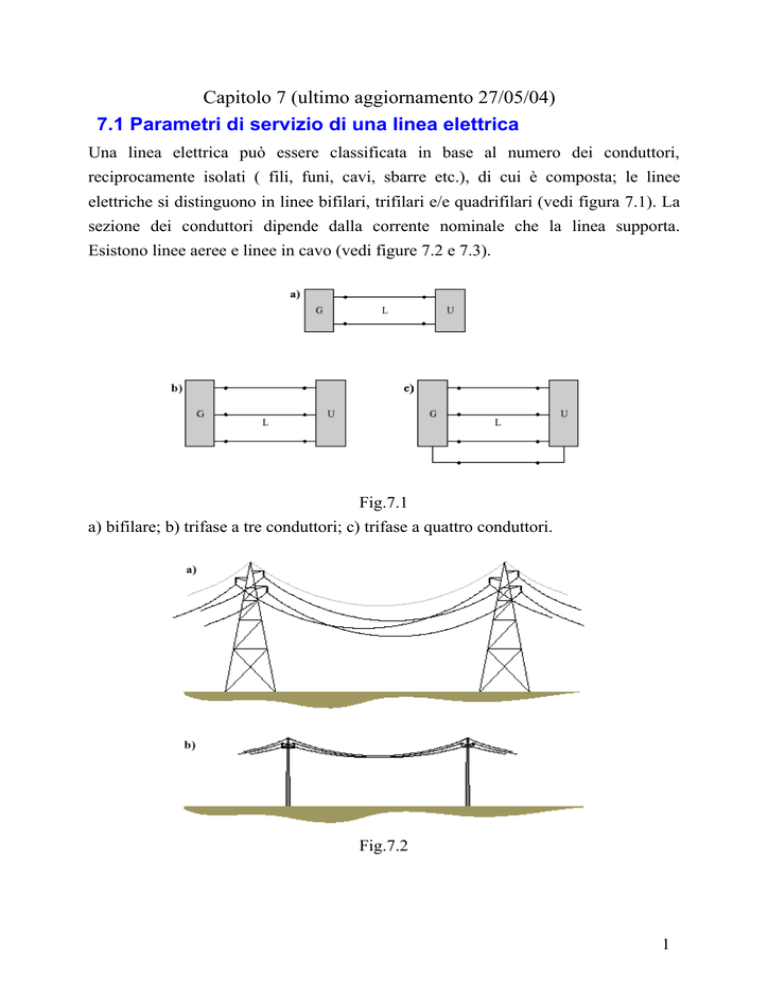
elettriche si distinguono in linee bifilari, trifilari e/e quadrifilari (vedi figura 7.1). La
sezione dei conduttori dipende dalla corrente nominale che la linea supporta.
Esistono linee aeree e linee in cavo (vedi figure 7.2 e 7.3).
Fig.7.1
a) bifilare; b) trifase a tre conduttori; c) trifase a quattro conduttori.
Fig.7.2
1
Fig.7.3
Tipologie di membratura di distribuzione dell’energia elettrica: figura 7.2 a) aerea
A.T. ; b) aerea B.T.; figura 7.3 in cavo con varie sezioni e configurazioni.
7.2 Schema elettrico equivalente di una linea bifilare
7.2.1 Il modello e i parametri dello schema
Con riferimento ad un tratto di linea bifilare di lunghezza , di sezione circolare S e
di raggio r 0 con i conduttori paralleli tra loro posti, ad una distanza h tra i centri
delle due sezioni, lo schema elettrico equivalente è riportato in figura 7.4.
Fig.7.4
Resistenza longitudinale
R
2
S
Induttanza longitudinale
L ln rh 1
4
0
Capacità trasversale
C
hr
ln r 0
0
Conduttanza trasversale
Trascurabile nel caso di linee aeree e per cavi in buone condizioni.
Nella pratica per gli impianti di media e bassa tensione si preferisce ricorrere al
seguente schema semplificato:
2
Fig.7.5
Nelle applicazioni della bassa tensione, oggetto di interesse del nostro corso, gli
effetti dovuti alla capacità trasversale ed alla conduttanza trasversale sono il più delle
volte trascurabili ( gli effetti della capacità trasversale non sono trascurabili solo ai
fini della sicurezza per le correnti di richiusura a terra).Pertanto si introducono i
seguenti paramentri elettrici equivalenti: resistenza di servizio R s ed induttanza L s di
servizio, così definiti:
2
R
per linee bifase
S
R
per linee trifase
S
L ln rh 1
per linee bifase
4
0
ln rh 1
per linee trifase
L
4
2
0
Una nota a parte deve essere fatta per la capacità di servizio C s che è legata alle
capacità tra conduttori e tra i conduttori e la terra, ad esempio nel caso bifilare si ha:
Fig.7.6
C s C t 2C 12
Formule analoghe si possono introdurre per una linea trifase.
3
7.2.2 Formula pratica
Con riferimento alla figura 7.7, la caduta di potenziale associata alla membratura
bifilare di collegamento tra il punto di fornitura e l’utente, è pari a:
Fig.7.7
|U| |Ū p Ū a | R s I cos X s I sin 7. 1
La formula 7.1 è facilmente determinabile osservando la figura 7.8 nelle ipotesi in
cui cos 0. 6, infatti:
Fig.7.8
|Ū p Ū a | AC AB B C RI cos XI sin
4
7.3 Calcolo e/o verifica di una membratura elettrica mediante
il metodo del momento d’erogazione
Si definisce " membratura", l’insieme di cavi o sbarre o conduttori che partono da
una cabina di trasformazione per arrivare fino al singolo utente. Le operazioni su una
membratura possono essere di due tipi:
- calcolo preliminare o di progetto
- calcolo di verifica
Nel primo caso si deve scegliere la sezione del conduttore in modo che vengano
rispettate le due condizioni:
a) la corrente che transita sia sempre inferiore a quella che dà un riscaldamento
superiore al massimo ammissibile per il tipo di membratura e il tipo di posa in opera
(interrata, all’aria libera, in canalina etc.).
b) la c.d.p. (caduta di potenziale) nel cavo deve essere inferiore alla massima c.d.p.
prefissata DV max .
Nel secondo caso, occorre solamente verificare che nel conduttore la massima c.d.p.
per la configurazione sotto analisi sia inferiore al valore DV max prefissato.
7.3.1 Metodo iterativo
Nel caso di cavi e/o conduttori nudi, disponendo di una tabella del tipo di quella
allegata (vedi tabella 1), con dati riguardanti: la sezione del conduttore, la corrente
ammissibile e i parametri di servizio r, x [/km], forniti dal costruttore, si può
facilmente procedere come segue:
A) Verifica
Fig.7.9
V tot V AB V BC . . . . . V MN
dove:
5
V AB r AB L AB I 1 cos 1 I 2 cos 2 . . . . . I n cos n
x AB L AB I 1 sin 1 I 2 sin 2 . . . . I n sin n
V BC r BC L BC I 2 cos 2 . . . . . I n cos n x BC L BC I 2 sin 2 . . . I n sin n
.........................................................................................
.........................................................................................
V MN r MN L MN I n cos n x MN L MN I n sin n
con le lunghezze L AB , L BC ,......, L MN espresse in km.
B) Progetto
Preliminarmente si determina la massima corrente che attraversa il primo tratto del
cavo con la seguente formula:
I max I 1 cos 1 I 2 cos 2 . . I n cos n 2 I 1 sin 1 I 2 sin 2 . . I n sin n 2
In seguito si sceglie dalla tabella 1 (alla fine del capitolo) la sezione del cavo che sia
in grado di sopportare, nelle particolari condizioni di posa, la corrente così trovata e
quindi si determina la caduta di potenziale V max e si verifica se essa è della
V max ammissibile.
Se superiore al valore prefissato si prende la sezione immediatamente superiore e si
ripete iterativamente fino al raggiungimento della c.d.p. desiderata. Nel caso in cui
non si trovasse la sezione idonea, si possono prendere due o più conduttori da porre
in parallelo onde soddisfare la condizione termica.
Il metodo consente comunque di soddisfare preliminarmente la condizione termica e
poi quella funzionale.
Nel caso in cui non si disponga di un catalogo, per il progetto e/o la verifica delle
membrature, si può procedere con il metodo dei momenti, illustrato in seguito.
Simbologia, unità di misura e valori per un calcolo di prima approssimazione:
1
2
1 k 50 55 mm m
25 29 1 m mm 2
Cu
Al
7. 2
- lunghezza in metri (m
- S (sezione) in millimetri quadrati (mm 3
- DV (caduta di potenziale) in Volt (V)
- I (corrente) in Ampere (A) in cc è il valore massimo, in ca è il valore efficace.
- R, X sono rispettivamente la resistenza e la reattanza per unità di lunghezza.
Il primo valore è relativo al caso di cavi, il secondo si riferisce ai conduttori privi di
6
guaina (*).
Momento d’erogazione: è il prodotto della corrente assorbita dal carico per la
distanza dal punto di fornitura ed ha le dimensioni di [Am], ovvero [kAm].
Per comprendere meglio l’algoritmo del momento d’erogazione, consideriamo prima
solo i casi in cc, ovvero in corrente alternata ma con cos 1, per poi passare alla
generalizzazione.
7.4 Membratura aperta alimentata ad una estremità dc o ac
(con cos 1)
Fig.7.10
I erogazione
lunghezza della membratura (la membratura può essere in cavo o in linea aerea)
La c.d.p.(caduta di potenziale) vale per una linea bifilare :
DV RI 1 I I M 7. 3
kS
k S
kS
da cui:
DV M Volt
7. 4
kS
ovvero la formula inversa:
S M mm 2
7. 5
kDV
Esempio 1: Verificare se la caduta di potenziale è inferiore al 2.5% (V % ) del
valore nominale per il caso di figura 7.11, avendo scelto per la membratura un
conduttore nudo.
Fig.7.11
I P/V 15000/220 68A
(*) nota: nei sistemi monofasi la lunghezza va moltiplicata per 2 per tenere
conto della andata e del ritorno.
7
MA I 68 2 150 20400 A m
(il fattore 2 per l’andata ed il ritorno)
MA
20400 6V
DV
5563
kS
DV % 6 100 2. 727%
220
DV % DV amm. 2. 727% 2. 5%
La membratura non soddisfa le ipotesi di lavoro, quindi bisogna aumentare la
sezione S oppure ridurre la potenza assorbita!
Esempio 2: come il caso precedente ma con una linea trifase di figura 7.12:
Fig.7.12
I P/ 3 V cos
15000
23A
3 3801
MA 23 150 3450 A m
MA
3450 1V
DV
5563
kS
1
DV%
100 0. 45%
220
DV amm 2. 5%
DV% DV amm %
8
7.5 Membratura alimentante più carichi a sezione costante e
cos 1
Fig.7.13
a) Verifica
DV
n I
i1
i i
kS
n M A
i1
i
kS
7. 6
b) Progetto
n I
i1
i i
n M A
i1
i
7. 7
DVk
kDV
Esempio 3: Verifica della membratura bifilare di figura 7.14 con DV amm 2%
S
alimentata a 125 V:
Fig.7.14
M 1 A 10 2 20 400 A m
9
M 2 A 10 2 50 2000 A m
M 3 A 5 2 90 900 A m
M 4 A 10 2 110 2200 A m
4 M A 5500 A m
i1
i
4 M A
i1
i
DV
5500 2V
5550
kS
DV% 2 100 1. 6%
125
DV% DV amm
Esempio 4: Determinare la sezione ammissibile per la membratura trifase alimentata
a 220/127 V con un unico cavo di Cu isolato in gomma a sezione costante di figura
7.15 alimentante più carichi con DV amm 0. 5% .
Fig.7.15
I1
1500
3 2201
3. 9 A
I2
2000
3 2201
5. 3 A
I3
1000
3 2201
2. 6 A
M 1 A 3. 9 50 195 Am
M 2 A 5. 3 70 371 Am
M 3 A 2. 6 100 260 Am
M i A 2. 6 100 826 Am
DV am 0.5127 0. 64 V
100
826
25. 8 mm 2
S M i A/kDV
500.64
10
S commerciale 25mm 2
A questo punto è necessario verificare sulle tabelle dei cavi, se la sezione
S 25mm 2 è idonea a sopportare la corrente massima pari a: 3.95.32.611.8A,
altrimenti si deve adottare la sezione più grande.
7.6 Membratura alimentante più carichi a sezione variabile
con cos 1
Con riferimento al caso precedente qualora si volessero usare spezzoni di cavo di
sezione via via decrescente, occorrerebbe trovare le S 1 , S 2 , S 3 . . . . . . S n sezioni, ma
questo caso così come formulato è un problema indeterminato, per renderlo
determinato occorre introdurre le seguenti ipotesi di lavoro:
Fig.7.16
a) La massima c.d.p. all’estremo "n" deve essere inferiore o uguale alla DV amm .
b) La corrente I
1 che fluisce in ogni tratto della membrana deve essere sempre
inferiore alla massima corrente ammissibile per il cavo.
c) Deve essere minimo il volume di materiale conduttore impiegato e cioè:
1 S 1 2 S 2 . . . . . . n S n minimo 7. 8
Con tali ipotesi si può dimostrare che le sezioni devono soddisfare le seguenti
relazioni:
S1 I
1
S2 I
2
S3 I
3
Sn I
n
con I
1
con I
2
con I
3
con I
n
I 1 I 1 . . . . I n
I 2 I 3 . . . . I n
I 3 I 4 . . . . I n
7. 9
In
ove:
11
i I i
kDV
7. 10
Svantaggi:
1. Il costo del conduttore posato in opera non è proporzionale al volume del
conduttore stesso. Per i cavi con isolamento, in particolare, il costo non cresce nella
stessa proporzione della sezione, infatti un cavo di sezione doppia non costa il
doppio di metà sezione.
2. Le sezioni ottenute dai calcoli sono diverse da quelle commerciali, per cui spesso
la funzione minimizzata (volume di conduttore) perde gran parte del suo significato
3. Aumentano in misura notevole gli "sfrasi", cioè gli avanzi di matassa di cavo, con
dubbio reimpiego degli spezzoni.
4. La membratura rimane troppo rigida sotto il profilo elettrico, per cui qualsiasi
modificazione futura degli assorbimenti potrebbe comprometterne l’ottimizzazione.
5. Si dovrebbero installare "n" protezioni da sovraccarico, una per ogni tronco a
diversa sezione.
6. Ogni giunzione è un punto di debolezza della rete per eventuali ossidazioni: il
costo di una giunzione non è trascurabile.
7. Qualora si considerasse l’ipotesi di alimentazione anche da un’altra cabina
(maggiore affidabilità della fornitura), sarebbe preclusa l’alimentazione di rovescio.
Esempio 5: con riferimento alla configurazione trifase 220/127 V di figura 7.17
progettare la membratura con tre sezioni diverse con cavo isolato in gomma e con
DV max 0. 5% .
Fig.7.17
I 1 1500/ 3 220 1 3. 9A
12
I 2 2000/ 3 220 1 5. 3A
I 3 1000/ 3 220 1 2. 6A
M 1 A 3. 9 50 195A m
M 2 A 5. 3 70 371A m
M 3 A 2. 6 100 260A m
3 M A 826 A m
i1
i
DV max 0. 5 127/100 0. 635V
3 M A
i1
i
826
25. 8mm 2
S
500.64
kDV max
S commerciale 25mm 2
I amm 60 A da tabella 1, contro I
1 3. 9 5. 3 2. 6 11. 8A
1/2
1 I
1 50 11. 8 171 A m
1/2
2 I
2 20 7. 9 56 A m
1/2
3 I
3 30 2. 6 48 A m
3 I 275A 1/2 m
i1
i 1
3 I
i1
i 1
275
8. 6
500.64
kDV amm
2
S1 I
1 8. 6 11. 8 29. 4 mm
S2 I
2 8. 6 7. 9 24. 2
S3 I
3 8. 6 2. 6 13. 8
S 1 dovrebbe essere commercialmente 40mm 2 , con una
assolutamente fasulla.
ottimizzazione
Il volume teorico di rame è:
29. 4 50000 24. 2 20000 13. 8 30000 2. 368 10 6 mm 3
Il volume effettivo commerciale è:
40 50000 25 20000 16 30000 2980 000mm 3 3m 3
13
7.7 Membratura alimentata ad una estremità in dc e/o ac (cos
1) con più diramazioni
DVC 1 DV AB DV BC
1
DVC 2 DV AB DV BC
2
7. 11
DVC 3 DV AB DV BC
3
Fig.7.18
A) Calcolo di verifica:
E’ semplice, basta applicare il principio di sovrapposizione degli effetti e verificare
che
DV max DVC 1 , DVC 2 , DVC 3
B) Calcolo preliminare
Problema indeterminato, per renderlo determinato occorre fare le seguenti ipotesi di
lavoro:
S0 S1 S2 S3
DVC 1 DVC 2 DVC 3 ) DV amm
Da questa seconda ipotesi si può ricavare immediatamente la seguente
14
configurazione fisica equivalente:
Fig.7.19
ove I i sono le correnti di tutte le diramazioni e è la lunghezza virtuale della
membrana principale (quindi di sezione S 0 ) che deve essere aggiunta a quella fisica
AB .
Per il calcolo si opera come segue:
3 M B
j1
j
ove j1,2 e 3, cioè solo le diramazioni.
Ii
In virtù di tale equivalenza il problema di progetto si riduce alla seguente
configurazione:
Fig.7.20
MA AB I i
S0
kDV
7. 12
da cui:
S1
M 3 B
M 1 B
M 2 B
S0 S2
S0 S3
S
3 M B
3 M B
3 M B 0
j1
j
j1 j
j1 j
7. 13
15
Esempio 6: membratura monofase con V A 220V ,
cos 1 (figura 7.21).
D max 0. 8%
e con
Fig.7.21
n.b. La linea è monofase, per cui le lunghezze geometriche debbono essere
moltiplicate per 2.
Calcolo di :
diramazione 1
diramazione 2
diramazione 3
10 10 100 Am
5 20 100 Am
10 20 200 Am
5 30 150 Am
10 40 400 Am
5 30 150 Am
5 40 200 Am
M 2 B 500 Am
M 3 B 350 Am
M 1 B 450 Am
da cui
M i B 450 500 350 1300 Am
I
B I 1 I 2 I 3 20 15 15 50A
M i B
da cui
1300/50 26m
I
B
16
Determinazione di S 0 :
DV amm 220 0. 8 1. 76 V
100
quindi
MA 10 20 15 50 50 142 8050 Am
da cui:
8050 91. 5 mm 2
501.76
Determinazione di S 1 , S 2 , S 3 :
S0
M 1 B
S 0 450 91. 5 32 mm 2
1300
M i B
M 2 B
S2
S 0 500 91. 5 35 mm 2
1300
M
B
i
M 3 B
S 0 350 91. 5 25 mm 2
S3
1300
M i B
le sezioni della membratura saranno quindi:
S 0 100 mm 2 ; S 1 S 2 35 mm 2 ; S 1 25 mm 2
S1
17
7.8 Membratura alimentata alle due estremità alla stessa
tensione V e con cos 1
7.8.1 Carico singolo
Fig.7.22
ipotesi: V A V B
I A corrente erogata dalla cabina A
I B corrente erogata dalla cabina B
ovviamente:
I A I B I con
I B L AB IL A0 0
I A L AB IL B0 0
7. 14
da cui:
I B L A0 /L AB I
I A L 0B /L AB I
7. 15
ne discende che la membratura può essere analizzata elettricamente studiando
indipendentemente una sola delle due sottomembrature:
Fig.7.23
18
7.8.2 Carichi multipli
Fig.7.24
La corrente erogata dalla cabina A sarà:
I A I 1 L 1B I 2 L 2B I 3 L 3B L AB
La corrente erogata dalla cabina B sarà:
7. 16
I B I 1 L 1A I 2 L 2A I 3 L 3A L AB
7. 17
ed è ovviamente:
3 I
I A I B i1
7. 18
i
Analogamente alla ricerca del punto di inversione del taglio in Scienza delle
Costruzioni per una trave appoggiata, nel caso elettrico è necessario trovare il carico
che è contemporaneamente alimentato da A e da B e quindi tagliare elettricamente la
membrana in quel punto indi procedere in modo separato.
Esempio 7: vedi figure 7.25 e 7.26.
Fig.7.25
I A 10 80 20 30 10 10/100 15A
la membratura si spezzerà a due a 70m da A, così:
19
Fig.7.26
7.9 Membratura chiusa
Nel caso in cui V A V B si considera la membratura come fosse alimentata a due
estremi distinti e quindi si procede come nel caso precedente.:
Fig.7.27
Fig.7.28
Esempio 8: membratura trifase ad anello chiuso,con cavo in gomma etilpropilinica,
con V380/220V, con cos1 e con DV amm 1. 5% (figure 7.29 , 7.30 e 7.31).
20
Fig.7.29
Fig.7.30
Calcolo delle correnti:
I 1 P 1 / 3 Vcos 1 20000/ 3 380 30. 4 A
I 1 10000/ 3 380 15. 2 A
I 1 15000/ 3 380 22. 8 A
determinazione I :
A
I 30. 4 150 15. 2 100 22. 8 40/170 41. 2 A
A
La membratura si spezza in corrispondenza del secondo carico come indicato in
figura 7.31:
Fig.7.31
Tenendo conto che DV amm 1.5220 3. 3 V la sezione della membratura vale:
100
30.42010.870
8. 3mmm 2
S
503.3
21
Si spezza la membratura in AB e come in figura 7.31 si ha una membratura
allineata ai due estremi.
7.10 Le membrature con carichi aventi fattore di potenza
diverso da 1
Occorre distinguere il calcolo di verifica dal progetto preliminare.
Ricordiamo la formula approssimata per il calcolo della DV amm
DV amm RI cos XI sin RI f XI DV R DV X
7.10.1 Verifica di una membratura aperta ed alimentata ad una sola
estremità
Fig.7.32
In un primo tempo si assegna alla X reattanza, il valore che deriva dalla tabella del
costruttore, e si procede nel calcolo della DV x .
Dopo aver calcolato il valore della c.d.p., dovuta alla componente reattiva, si sottrae
tale valore alla DV tot
DV R DV tot DV x
Si procede quindi alla verifica della membratura pensando di avere come carichi
(correnti) le sole componenti in fase I fi i 1, 2, 3. . . n.
Analogamente si procederà nel caso di progetto, con la differenza che in questo caso,
si adotterà un valore di x arbitrario da verificare in seguito con il valore reale.
22
Progettata la sezione S si ricalcola il valore della X e quindi della DV x effettiva. Nel
caso la DV tot non risulti entro i limiti si riprocede nella stessa maniera con un’altra
iterazione con una sezione maggiore.
In modo del tutto analogo si procede avendo a disposizione una tabella di
cavi/conduttori con corrente ammissibile e valori di r e x come in tabella 1,
eseguendo una scelta preliminare in funzione della portata e poi verificare a
posteriori la c.d.p.
Il metodo è sicuramente rapidamente convergente.
7.10.2 Progetto di una membratura aperta ed alimentata ad una
estremità
La reattanza di servizio X può essere calcolata in prima approssimazione noto:
-il livello di tensione della linea
-il tipo di membratura ( aerea o in cavo)
Esempio 9: per una linea aerea trifase:
L
ln rD 1 mH/km
2
4
0
per D 1 m
d 1 5 mm o d 2 15 mm
S 1 20 mm 2 S 2 176 mm 2
L 1 0. 063 mH/km
L 2 0. 052 mH/km
Esempio 10: calcolo di verifica della membratura trifase 10kV di conduttori di rame
nudo con una V amm 3%
S 40mm 2 e D 60cm (figure 7.33 e 7.34).
Fig.7.33
P
3 V cos
If P
3V
I
23
Iq
P
sin
3 V cos
P tan g I tan g
f
3V
I f 150000/ 3 10000 8. 7A
I q 8. 7 tan g 8. 7A
L 10 4 0. 25 ln 600
7.136
S 40mm 2 d 7mm
4. 681 8 10 4 mH/km
da cui X 314 30 4. 681 8 10 4 4. 410 3
Fig.7.34
DV X X I q 4. 410 3 8. 7 38. 370
I f 3010 3
DV R
8.730000 118V
5540
kS
DV tot DV R DV X 38. 370V 118V 118V 38. 37V 156. 37V
DV max % 156. 37 100 2. 708 4%
10000
3
DV max % DVamm
Se il risultato fosse stato diverso, si sarebbe dovuto ricorrere ai seguenti rimedi:
a) aumento della sezione del conduttore
b) mettere in parallelo un’altra membratura
c) rifasare il carico: aumentando il cos diminuisce DV X (N.B. per cos 1,
DV X 0!
Q
3 VI sin
3 10000 8. 7 150kVAR
d) compensare la reattanza induttiva della rete inserendo in serie alla linea una
batteria di condensatori
24
Fig.7.35
I
P
150000/
3 V cos
3 10000 0. 7
12. 3A
V L DV C 10. 2 12. 3 126V
da cui
Q 3DV C I 3 126 12. 3 4. 65kVAR
e) inserire all’arrivo un autotrasformatore di potenza apparente tale da annullare la
caduta in arrivo.
In altri termini si tratta di aumentare la tensione in arrivo con un autotrasformatore
elevatore, con la seguente potenza di targa:
3.6% di 150 kW
P n 3.6 150000 7714. 3VA 8kVA
0.7
100
25












