LA LEZIONE
Analisi di un crash test
I filmati delle prove d’impatto distruttive degli autoveicoli, dato l’elevato numero dei
fotogrammi al secondo, riportano la scena dell’urto al rallentatore con l’indicazione del
tempo in millesimi di secondo. In un crash test frontale pieno (figura 1) l’auto, lanciata
alla velocità standard di 56 km/h (15,56 m/s), urta una barriera di alluminio larga un
metro e profonda 54 centimetri. L’angolo tra la direzione del moto (chiamiamolo asse
x) e il piano d’impatto della barriera è di 90°. Dal punto di vista del manichino,
l’accelerazione iniziale è nulla (moto rettilineo uniforme), nell’istante dell’urto la sua
testa subisce un’accelerazione (dovuta a una forza apparente) che ha tre componenti
rispetto alla barriera (ax trasversale, ay longitudinale e az verticale). Il modulo
dell’accelerazione (dovuto principalmente alla componente trasversale) in pochi decimi
di secondo raggiunge un massimo per poi decrescere fino a valori prossimi a zero, sia
per l’azione delle cinture e dell’airbag (fig. 2), sia per l’arresto dell’auto.
Esaminiamo solo la fase di avanzamento della testa del conducente verso il volante con
le misure del grafico della figura che segue, ottenuta grazie agli accelerometri disposti
nell’autovettura, in unità multiple dell’accelerazione di gravità (g=9,8 m/s 2).
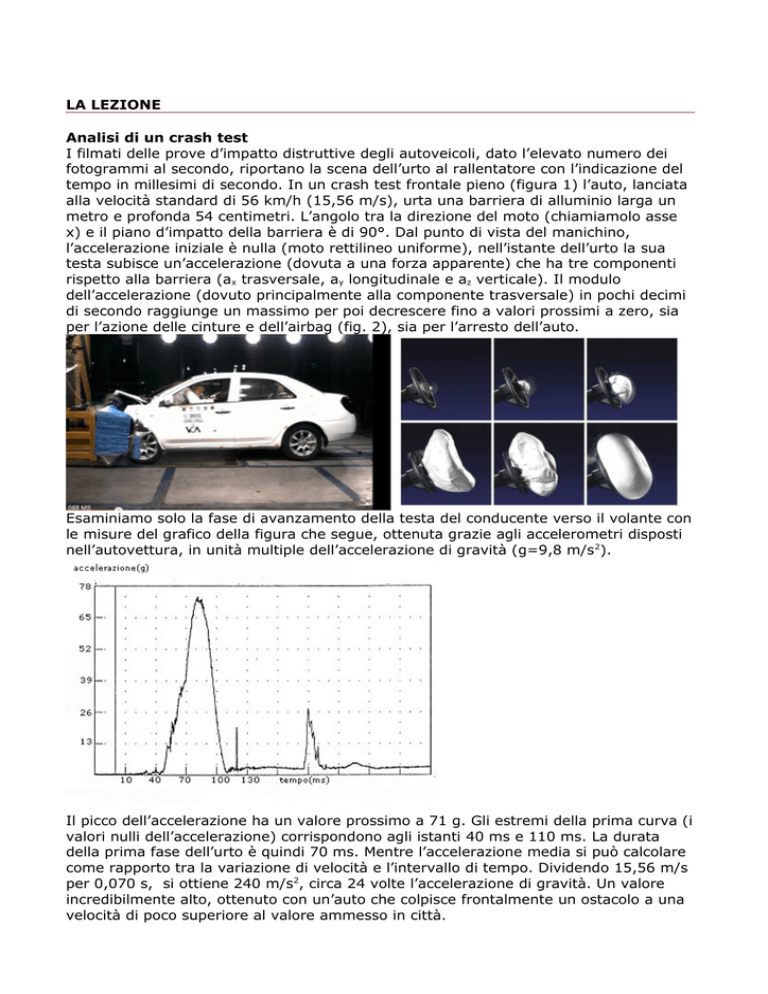
Il picco dell’accelerazione ha un valore prossimo a 71 g. Gli estremi della prima curva (i
valori nulli dell’accelerazione) corrispondono agli istanti 40 ms e 110 ms. La durata
della prima fase dell’urto è quindi 70 ms. Mentre l’accelerazione media si può calcolare
come rapporto tra la variazione di velocità e l’intervallo di tempo. Dividendo 15,56 m/s
per 0,070 s, si ottiene 240 m/s2, circa 24 volte l’accelerazione di gravità. Un valore
incredibilmente alto, ottenuto con un’auto che colpisce frontalmente un ostacolo a una
velocità di poco superiore al valore ammesso in città.
Per noi osservatori esterni l’incidente è causato dalla barriera che esercita una forza
sull’auto provocando una decelerazione del centro di massa del sistema (veicolo
conducente). L’intensità della forza si può calcolare a partire dalla massa del sistema
(auto più manichino) utilizzando il secondo principio della dinamica: F=ma. Il valore
medio della forza si otterrà dal valore medio dell’accelerazione. Se si pone a esempio
per la massa totale un valore indicativo di 1300 kg, la forza media nell’esempio risulta
circa 289 kN. Durante l’impatto avviene la trasformazione di parte dell’energia cinetica
dell’auto in energia termica e di deformazione dell’auto stessa e della barriera (la parte
elastica produce il rimbalzo dell’auto). Limitandoci all’intervallo di tempo tra 40 e 110
ms e approssimando il movimento lungo la sola direzione x, il lavoro L della forza F media
è uguale a -Fmedia DxG (la forza è opposta allo spostamento DxG del centro di massa).
Valutare lo spazio percorso dal centro di massa è assai difficile (tenuto conto delle
molteplici deformazioni). Nei calcoli che seguono, lo porremmo, in modo arbitrario,
esattamente uguale alla profondità dell’ostacolo 0,54 m. Inserendo i valori trovati in
precedenza, il lavoro L=-289 kN 0,54 m=-156 kJ, mentre la variazione di energia
cinetica è :
Kf-Ki=0-mv2/2=-1300 kg (15,56 m/s)2/2=-157 kJ (si tenga presente che le barriere di
contenimento delle strade italiane difficilmente sono capaci di respingere autoveicoli
con energia cinetica di 400 kJ in un urto frontale). I valori trovati sono uguali. 1
Impulso e quantità di moto
Il secondo principio della dinamica può essere espresso in un’altra forma per descrivere
lo studio delle collisioni tra due corpi. Ritornando al crash test, la forza ha un
andamento nel tempo che ricalca quello dell’accelerazione, ma la misura della forza
media non basta per descrivere in modo completo l’urto. Nella figura che segue, l’area
delimitata dalla curva (del grafico tempo forza) è l’intensità di una nuova grandezza
chiamata impulso I ed è equivalente all’area del rettangolo i cui lati misurano la durata
dell’urto Dt e l’intensità della forza media: I=FmediaDt.
A parità di impulso la definizione precedente indica la proporzione inversa tra forza
(media) e durata dell’urto. Così la trasformazione, durante l’urto, dell’energia cinetica
in altri tipi di energia può avvenire, come è immediatamente chiaro, in diverse
modalità. Se il corpo e le barriere sono realizzati con materiali capaci di massimizzare
l’interazione, con una durata elevata, la forza è minima; viceversa, se, cambiando a
1
L’uguaglianza tra i due termini non dipende dalla massa scelta.
esempio la barriera, la durata è minore rispetto al caso precedente, l’intensità della
forza cresce, poiché l’impulso dipende solo dalle condizioni di moto iniziali e finale
dell’auto.
L’equazione I=FDt=mDv rappresenta un modo diverso di esplicitare il secondo principio
nei problemi di movimento e la grandezza mDv è detta variazione della quantità di
moto totale del sistema.
Consideriamo adesso due corpi (ugualmente rilevanti) lanciati l’uno contro l’altro (due
palle di biliardo, due cariche elettriche, due particelle) che avvicinandosi (toccandosi)
interagiscono fortemente per un tempo molto breve. Le intensità, uguali, delle due
forze d’interazione sono, in genere, molto più grandi delle intensità delle forze esterne
(nel caso del crash test la forza media è pari a 24 volte il peso dell’auto). In questo
modo il sistema costituito dalla coppia di oggetti in interazione è detto isolato e la
quantità di moto totale del sistema non cambia durante la collisione (anche se la
velocità dei singoli corpi può variare). Si simulano così gli urti elastici e anelastici (per i
quali si conserva anche l’energia cinetica) di ideali sferette (si veda la figura 5), ma
anche l’interazione di particelle subatomiche, in modo tale che il centro di massa del
sistema rimanga invariato.
figura 5
Urti di protoni ad alta energia producono particelle che a loro volta decadono in altre
particelle, tutte aventi la stessa origine nel centro di massa. Le posizioni (individuate
dalla tracce), le masse e le quantità di moto2 divengono le misure standard iniziali
anche della fisica degli acceleratori.
La diffusione di Rutherford (dal punto di vista della meccanica classica)
Le esperienze sulle particelle elementari sono tutte basate sulle collisioni di coppie di
particelle. L’idea base degli esperimenti è assai semplice, si cerca di realizzare un
“crash test” che coinvolga solo un fascio di particelle e un bersaglio (target) oppure due
fasci di particelle (2 auto una contro l’altra) di energia elevata. Gli studi del fisico
neozelandese Ernest Rutherford, già premio Nobel per la Chimica nel 1908 per le sue
ricerche in Canada sulla disintegrazione degli elementi e sulla chimica degli elementi
radioattivi, nel laboratorio di Manchester tra il 1909 e il 1911 rappresentano un
esempio di questa pratica. La diffusione di particelle alfa (prodotte da radio e collimate
da una fenditura realizzata su uno schermo di piombo) incidenti su fogli metallici di
spessore limitato è studiata da Rutherford e dai suoi collaboratori attraverso ore e ore
di osservazione di brevi lampi provocati su una sostanza fluorescente (solfuro di zinco)
2
La quantità di moto di una particella (e per certi versi la massa) è definita in una forma diversa che
vedremo in una successiva lezione.
disposta lungo una superficie concentrica al bersaglio (si veda la schema e la foto che
seguono).
Le misure portano Rutherford a proporre il primo modello di atomo con nucleo centrale
positivo di dimensioni trascurabili rispetto a quelle dell’atomo stesso. Analizziamo un
caso particolare proposto dagli assistenti di Rutherford, Hans Geiger (tedesco) e Ernest
Marsden (neozelandese), nel 1911. Tra tutte le interazioni tra particelle alfa e nuclei del
metallo (diciamo oro) i due ricercatori notano la possibilità di particelle alfa riflesse
nella stessa direzione iniziale: il caso di un urto frontale elastico unidimensionale.
Indichiamo con i simboli mA e mB le masse dei corpi che interagiscono, vA(0) e vB(0) le
velocità iniziali delle particelle al tempo zero, vA(t) e vB(t)le velocità al tempo t dopo
l’urto. Per il principio di conservazione della quantità di moto dev’essere:
mA vA(0) + mB vB(0) = mA vA(t) + mB vB(t). Mentre per il principio di conservazione
dell’energia: mA vA2 (0) + mB vB2 (0) = mA vA2 (t) + mB vB2 (t) (il termine ½ è stato
semplificato). Una delle soluzioni banali del sistema e quella in cui la velocità di ogni
singola particella sia uguale prima e dopo l’urto. Per trovare la seconda soluzione, non
ovvia, ipotizziamo una velocità iniziale dell’atomo bersaglio uguale a zero. Le equazioni
di conservazione si trasformano nella forma:
mB vB(0) = mA vA(t) + mB vB(t)
mB vB2 (0) = mA vA2 (t) + mB vB2 (t).
È facile ricavare allora3:
vB(t)= vB(0) [(mB- mA)/(mA+ mB)]
vA(t)= vB(0) [2mB /(mA+ mB)] .
Mentre il termine che lega la velocità finale dell’atomo alla velocità iniziale della
particella alfa è per qualsiasi valore delle masse positivo, quello che esprime la velocità
finale della particella proiettile rispetto alla velocità iniziale della stessa particella è
negativo se mB< mA. In questo caso l’urto inverte il verso delle velocità della particella
alfa. I principi di conservazione sono compatibili con una situazione di rimbalzo se e
solo se il nucleo dell’atomo di oro ha una massa maggiore di quella delle particella alfa.
3
Esplicitando vB(0) nelle due equazioni, uguagliando il quadrato del primo termine al secondo e
semplificando.












