Antenne in ricezione

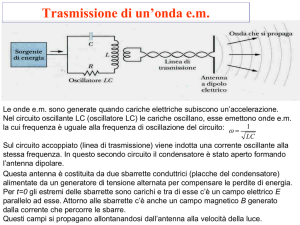
Antenne in ricezione
Prendiamo in considerazione una antenna immersa in un campo
elettromagnetico (Ei, Hi), detto campo incidente e “misurato” in assenza
dell’antenna. Supponiamo che l’antenna sia collegata ad un carico da una
struttura guidante schematizzata in Fig. 1 tramite una linea di trasmissione.
Ei , Hi
Js
A
B
A'
B'
λ
Fig. 1
Ipotizziamo inoltre che la struttura guidante sia sufficientemente lunga da
poter individuare su di essa due morsetti AA’ in cui i modi superiori che
vengono eccitati alla connessione dell’antenna per effetto di discontinuità,
transizioni e connettori, siano trascurabili.
La sezione AA’ viene detta sezione di ingresso dell’antenna e le funzioni
scalari di modo su AA’ (relative alla particolare struttura guidante utilizzata)
sono la tensione e la corrente in ingresso all’antenna.
L’interazione dell’antenna con il campo incidente produce un campo nella
struttura guidante e cioè il segnale viene condotto al carico.
Per caratterizzare l’antenna dal punto di vista del carico, possiamo utilizzare
il teorema di Thevenin ai morsetti AA’ guardando verso l’antenna:
A
Z ing
+
+
V0
A'
Fig. 2: Circuito equivalente di Thevenin dell’antenna in ricezione. Il
morsetto positivo è quello con corrente entrante quando l’antenna è in
trasmissione.
L’impedenza Zing è quella che si vede guardando dai morsetti AA’ in
assenza di campo incidente. Si tratta in sostanza della impedenza di ingresso
dell’antenna in trasmissione.
V0 prende il nome di tensione a vuoto e dipende dal campo incidente e dalla
corrente da esso indotta sull’antenna. La tensione a vuoto è l’integrale del
campo totale Etot sui morsetti dell’antenna e quindi dipende linearmente da
Etot = Ei + Es , dove Es è il campo dovuto alle correnti indotte che a sua volta
dipende linearmente dal campo incidente Ei. Di conseguenza, la tensione a
vuoto dipende linearmente da Ei.
Considereremo per semplicità solamente il caso in cui l’antenna sia investita
da un onda piana (o localmente piana nella zona dell’antenna). Data la
distanza tra l’antenna trasmittente e la ricevente nelle normali applicazioni è
generalmente lecito considerare l’onda in corrispondenza della ricevente
come un onda localmente piana.
In questo caso il campo elettromagnetico sui morsetti di ingresso
dell’antenna è completamente individuato dal valore del campo incidente Ei
e dal vettore d’onda k costante. Risulta pertanto:
Ei , k → V0
Poiché, come detto, la dipendenza dal vettore Ei è lineare, dovrà esistere un
vettore hr con le dimensioni di una lunghezza e dipendente da k tale che:
V0 = h r (k ) ⋅ E i
(1)
h r (k ) prende il nome di altezza efficace in ricezione dell’antenna.
La (1) vale ovviamente solo se l’onda incidente sull’antenna è un onda piana
perché in questo caso il campo incidente dipende da un solo parametro e non
da una funzione. In caso contrario V0 sarebbe l’integrale di tutto il campo
incidente e la sua espressione molto più complessa.
Esempio
(1)
Ei
k (1)
A
Antenna
V0
A'
(2)
Ei
k (2)
La sovrapposizione di due onde piane non è un onda piana ma per il
principio di sovrapposizione degli effetti si può scrivere:
V0 = h r (k ) ⋅ E i + h r (k ) ⋅ E i
(1)
(1)
(2)
(2)
Se il mezzo di trasmissione è reciproco (Isotropo) altezza efficace in
trasmissione e altezza efficace in ricezione coincidono purchè calcolate
nella stessa direzione
Dimostrazione
Per dimostrare l’eguaglianza delle altezze efficaci consideriamo la seguente
struttura:
Posso applicare il teorema di reciprocità a tutto lo spazio ad eccezione della
zona dell’utilizzatore/generatore L (superficie S, tratteggiata in rosso). AA’
sono i morsetti di ingresso dell’antenna.
Supponiamo che la linea e il blocco L siano schermati ossia racchiusi dentro
un C.E.P. Nell’ipotesi di mezzo isotropo, lineare e omogeneo nel tempo
applico il teorema di reciprocità in relazione alle seguenti due situazioni:
1) Antenna in trasmissione alimentata da una corrente I1, genera un campo
E1, H1 (in questo caso il blocco L è un generatore)
2) Antenna a vuoto in ricezione (in questo caso il blocco L è un carico).
Riceve il campo lontano di un dipolo elementare:
J D = I D ∆z δ ( r − r D ) i D
(1)
con i D ortogonale alla direzione della congiungente trasmittente-ricevente.
Applichiamo il teorema di reciprocità:
∫
S'
( E 1 × H 2 − E 2 × H 1 ) ⋅ dS = ∫ ( E 2 ⋅ J 1 − E 1 ⋅ J 2 ) dV
V'
(2)
J1 sono le correnti che producono il campo in trasmissione e sono distribuite
sulla superficie dell’antenna trasmittente che è un C.E.P., quindi, poiché il
campo elettrico E2 del dipolo è ortogonale al C.E.P. antenna, risulta
E 2 ⋅ J 1 = 0 . La corrente J2 è la corrente del dipolo elementare JD pertanto la
(2) diventa:
∫
S'
( E 1 × H 2 − E 2 × H 1 ) ⋅ dS = ∫ ( − E 1 ⋅ J D ) dV = − I D ∆z E 1 ( r D ) ⋅ i D (3)
V'
La superficie S’ è costituita:
1) dalla superficie tratteggiata sul C.E.P. che racchiude la linea e il
blocco L;
2) dalla sezione trasversa della linea di collegamento tra l’antenna e il
blocco L (in corrispondenza ai morsetti AA’);
3) dalla superficie all’infinito.
L’integrale a primo membro è dunque nullo su 1) e su 3). Per quel che
riguarda invece il contributo sulla superficie 2) si ha:
I campi trasversi alla sezione AA’ possono essere scritti nella forma:
E t = V ( z) e
H t = I ( z) h
dove e ed h sono le funzioni vettoriali di modo e V(z) e I(z) le funzioni
scalari di modo che nel nostro caso (ipotizziamo propagazione TEM)
coincidono con tensione e corrente sulla linea.
Il contributo all’integrale di superficie è pertanto:
∫
St
(V1 e × I 2 h − V2 e × I1 h ) ⋅ i n dS
(4)
V1 e I1 sono corrispondenti alla situazione in cui l’antenna è in trasmissione.
V2 e I2 sono corrispondenti alla situazione in cui l’antenna è in ricezione a
vuoto. Cioè I2=0 mentre V2 è la tensione a vuoto e cioè V0.
La (4) diventa pertanto
∫
St
E quindi dalla (3) si ottiene
( − Vo e × I1 h) ⋅ ( −i z ) dS
Vo I1 ∫ e × h ⋅i z dS = − I D ∆z E 1 ( r D ) ⋅ i D
St
∫
Ricordando che
St
e × h ⋅i z dS = 1 (flusso di potenza in una linea di
1
2
1
2
trasmissione P = V I * ∫S e × h ⋅i z dS = V I * ) si ha:
t
Vo I1 = − I D ∆z E 1 ( r D ) ⋅ i D
Vo =
− I D ∆z E 1 ( r D ) ⋅ i D
I1
E 1(r D ) =
j ζ I 1 − jβ
e
2 λ rD
(5)
rD
h trasm
(6)
Tenendo presente che il campo del dipolo in corrispondenza all’antenna
ricevente è un onda localmente piana si ha: Vo = h r ⋅ E = h r ⋅ E D , e cioè:
i
Vo = h r ⋅ E D = h r ⋅
π
jζ I D ∆z − jβ rD
e
sin( )( −i D )
2λ rD
2
(7)
In conclusione, per la (5), (6) e (7):
(Vo = ) h r ⋅
hr ⋅
π
− I D ∆z E 1 ( r D ) ⋅ i D
jζ I D ∆z − jβ rD
e
sin( )( −i D ) =
I1
2λ rD
2
jζ I D ∆z − jβ rD
π
e
sin( )( −i D ) =
2λ rD
2
− I D ∆z
jζ I 1 − jβ rD
e
h trasm ⋅ i D
2λ rD
I1
h r ⋅ i D = h trasm ⋅ i D
Che vale in qualunque direzione per qualunque valore di i D trasverso alla
congiungente l’antenna e il dipolo.
Da cui deriva che l’altezza efficace in ricezione è uguale alla altezza efficace
in trasmissione purchè siano calcolate nella stessa direzione.
Potenza ricevuta
Consideriamo una antenna in ricezione chiusa su un carico. Il campo
incidente è un onda piana di ampiezza Ei:
Ei , Hi
A
B
A'
B'
Zc
λ
Il circuito equivalente è il seguente:
A
Z ing
+
Zc
V0
A'
dove
V0 = h r ⋅ E i (8)
La potenza ricevuta dal carico Zc è pertanto:
2
2
V0
V0
1
1
P = Re( Zc)
= Rc
2
2
2 ( R + Rc )2 + ( X + Xc )2
Z ing + Zc
ing
ing
Per un fissato campo incidente la potenza può essere massimizzata variando
Zc o l’orientazione dell’antenna (ovvero la sua altezza efficace).
Rispetto a Zc il massimo si ottiene quando Zc = Zing* (in condizioni di
adattamento coniugato).
Per quanto riguarda l’altezza efficace, se ci limitiamo a considerare il caso di
un onda incidente localmente piana, dobbiamo osservare che V0 = h r ⋅ E i .
Poiché in generale sia hr che E i sono vettori complessi, per capire come si
può massimizzare il valore della tensione a vuoto V0 , è necessario definire
un prodotto interno in uno spazio di Hilbert complesso, definito come:
( A, B ) A ⋅ B *
2
( A, A) = A
2
A
B
,
( ) ≤ A B
(9)
(ovviamente ( A, B) A ⋅ B non è una definizione corretta perché A ⋅ A , se A è
complesso, non è reale e può essere nullo: ad es. se A = i x + ji y ).
Utilizzando la definizione (9.1) e la disuguaglianza Schwartz (9.3) possiamo
dunque scrivere:
(
V0 = h r ⋅ E i = h r , E i
*
)
(10)
V0 ≤ h r E i
Per la definizione di prodotto interno si ha inoltre
V0 = h r E i (11)
se
h r = α E i (12)
*
con α generico scalare complesso.
Il massimo di V0 si ha pertanto se vale la (12) che prende il nome di
condizione di adattamento in polarizzazione.
Si osservi che l’adattamento in polarizzazione richiede preliminarmente che
l’antenna e il campo incidente abbiano la stessa polarizzazione. Solo in
questo caso orientando opportunamente l’antenna ricevente è possibile
soddisfare la (12).
Se orentando l’antenna rendo vera la (12) posso affermare che l’antenna è
adattata in polarizzazione.
Esempio
Supponiamo di avere un onda piana incidente in polarizzazione lineare e una
antenna ricevente filiforme con altezza efficace in polarizzazione lineare.
Ei
k
θ
iθ
La posizione dell’antenna per avere adattamento in polarizzazione è tale da
disporre l’antenna nel piano formato dal vettore d’onda k e dalla direzione
del campo (o in un piano parallelo). In questo caso infatti l’altezza efficace è
parallela al campo elettrico incidente ed è senz’altro verificata la (12).
Per una antenna adattata al carico ed in polarizzazione la potenza massima
assorbita dal carico è dunque:
2
2
2
hr E i
hr E i
1
PM = Rc
=
2
4 Rc 2
8Rc
2
(13)
che è proporzionale al modulo quadro del campo incidente e quindi al
vettore di Poynting dell’onda incidente Si.
Si definisce AREA EFFICACE il rapporto tra la potenza consegnata al
carico in condizioni di adattamento al carico e in polarizzazione e il vettore
di Poynting associato all’onda incidente (purchè localmente piana):
A=
PM
Si
⇒ PM = A Si (14)
Poiché
Si =
1
2
Ei ,
2ζ
si ha:
h ζ
A= r
4 Rc
2
(15)
L’area efficace è un parametro che caratterizza una antenna in ricezione e
non è costante ma dipende dalla direzione (attraverso l’altezza efficace).
Spesso si intende per Area Efficace il massimo valore di A.
Daltra parte si osservi che anche il guadagno G (o la direttività D) di una
antenna sono proporzionali ad modulo quadro dell’altezza efficace:
πζ ht
G=
Ring λ 2
2
Nel caso di mezzo di trasmissione reciproco abbiamo dimostrato che
h t = h r e, tenendo presente che in condizioni di adattamento al carico Ring =
Rc, si ha:
2
4π ⎛ ζ h r ⎞ 4π
⎟=
G= 2 ⎜
A
λ ⎜⎝ 4 Rc ⎟⎠ λ 2
(16)
Per una antenna filiforme l’altezza efficace h è dell’ordine di grandezza
dell’antenna stessa (l’area efficace sarà dell’ordine di grandezza del
quadrato di h ma, per una antenna filiforme, non è facilmente
visualizzabile).
Se invece considero antenne di grosse dimensioni l’area efficace è
dell’ordine di grandezza dell’area fisica. Quindi il guadagno a parità di
dimensioni cresce con la frequenza.