A v - Dipartimento di Fisica

Paolo Bagnaia
Corso di Fisica
CTF (A-L)
A.A. 2002-2003
Paolo Bagnaia - CTF - Introduzione
♠
1
Orario 2003
Lezioni :
- lunedì
- martedì
- mercoledì
- giovedì
13-15
13-15
14-16
12-13
aula Conversi;
aula Magna;
aula Magna;
aula Magna.
Ricevimento :
Dip. Fisica, ed. Marconi, 2º piano, stanza 126;
martedì + mercoledì, ore 10-13.
Paolo Bagnaia - CTF - Introduzione
♠
2
Testi consigliati
• Halliday-Resnick-Walker
(edizione “breve” !!!)
• Tipler (… !!!)
• Serway (… !!!)
• [esercizi nel testo]
• Coluzza, Ferrari, Levi - Esercizi di Fisica
• Davidson - Metodi matematici per un corso
introduttivo di Fisica.
Paolo Bagnaia - CTF - Introduzione
♠
3
Sommario
• 1 - Meccanica - Cinematica, Statica, Dinamica.
• 2 - Meccanica dei Fluidi.
• 3 - Termodinamica.
• 4 - Elettromagnetismo - Elettrostatica, Correnti
elettriche, Fenomeni magnetici, Induzione, Ottica.
• 5 - Onde e Oscillazioni.
N.B. programma completo → guida della Facoltà
Paolo Bagnaia - CTF - Introduzione
♠
4
Programma 02-03 - pag. 1/5
1. Il metodo sperimentale – La misura e gli osservabili in fisica. Il sistema
unità di misura. Le dimensioni ed i cambiamenti di unità di misura. Rappresentazione
delle misure. Errori di misura e loro valutazione. Errori casuali e sistematici.
2. Cinematica – Sistemi di riferimento. Grandezze scalari e vettoriali. Velocità
istantanea. Il moto rettilineo uniforme. Il moto accelerato: moto uniformemente
Scomposizione dei vettori. Somma e prodotti tra vettori. Moto in più dimensioni.
uniforme: velocità angolare. Moti relativi.
3. Dinamica del punto – Definizione di forza. Prima legge della dinamica. I sistemi
riferimento inerziali. Seconda legge della dinamica. Terza legge della dinamica. I
lavoro: forze costanti, forze variabili. Teorema dell’energia cinetica. Potenza. Forza
elastiche. Forze di attrito: attrito statico e dinamico. Forze conservative. Energia
Conservazione dell’energia meccanica. Moti oscillatori e periodici. Il pendolo.
armonico: equazioni del moto e conservazione dell’energia.
Paolo Bagnaia - CTF - Introduzione
♠
5
Programma 02-03 - pag. 2/5
4. Sistemi di punti materiali – Il centro di massa. Leggi della dinamica per un
Impulso e quantità di moto. Conservazione della quantità di moto: caso
elastici ed anelastici in una dimensione.
5. Equilibrio dei corpi – Momento di una forza. Condizioni di equilibrio. Leve.
6. La gravitazione universale – Legge di Gravitazione. Leggi di Keplero.
7. I fluidi – Proprietà dei fluidi e dei liquidi. Densità e pressione. Principio di Pascal.
di Archimede. Legge di Stevino. Linee di flusso ed equazione di continuità.
dell’energia: equazione di Bernoulli. I liquidi reali: la viscosità. Moti laminari e
Legge di Hagen – Poiseuille. Legge di Stokes: velocità di sedimentazione.
8. Onde – Onde e particelle. Onde in una corda tesa. Lunghezza d’onda e frequenza.
Onde stazionarie. Onde acustiche. Ampiezza ed intensità di un onda.
Paolo Bagnaia - CTF - Introduzione
♠
6
Programma 02-03 - pag. 3/5
9. Calorimetria e Termodinamica – Il calore: misura ed unità di misura. Il calore
calore latente. La temperatura e le scale termometriche. Leggi di dilatazione termica.
zero della termodinamica. Primo principio della termodinamica. Leggi dei Gas
Trasformazioni isoterme, isocore, isobare ed adiabatiche. Teoria cinetica dei gas.
Avogadro. Calori specifici molari. Trasformazioni reversibili ed irreversibili. Cicli
termodinamici. Secondo principio della Termodinamica. Macchine termiche: ciclo di
Entropia e sue variazioni.
10. Elettrostatica – Cariche elettriche. Forze elettriche: legge di Coulomb. Struttura
e proprietà elettriche della materia. Il campo elettrico. Il dipolo elettrico. Legge di
potenziale elettrico. I conduttori e l’induzione elettrica. Capacità elettrica. Superfici
equipotenziali. Studio di alcuni esempi notevoli: campo elettrico generato da una
puntiforme, da distribuzioni di carica su fili, strati e doppi strati. I condensatori.
dell’energia immagazzinata in un campo elettrico.
11. Corrente elettrica e circuiti elettrici – La conduzione nei metalli. Densità di
Resistività e resistenza. Le leggi di Ohm. Energia e potenza nei circuiti elettrici.
tensione e di corrente. Circuiti elettrici in corrente continua. Carica e scarica dei
Paolo Bagnaia - CTF - Introduzione
♠
7
Programma 02-03 - pag. 4/5
12. L’elettromagnetismo – Il campo magnetico. Corrente elettrica e campo
di Biot e Savart. Legge di Ampere. Dipolo magnetico. Forza di Lorentz. Legge di
Legge di Lenz. Energia immagazzinata in un campo magnetico. Autoinduzione.
Equazioni di Maxwell (cenni). Onde elettromagnetiche. Velocità della luce. Il
Huygens.
13. Ottica geometrica – Limiti dell’ottica geometrica. Le leggi della riflessione e
rifrazione. Riflessione totale. Specchi piani. Specchi sferici. Diottro sferico. Lenti
Strumenti ottici.
Paolo Bagnaia - CTF - Introduzione
♠
8
Programma 02-03 - pag. 5/5
Bibliografia
Lo studente può utilizzare liberamente i libri di testo che ritiene più idonei a preparare
l'esame. Può fare riferimento ai testi seguenti, sia per la preparazione della prova orale
che di quella scritta :
• Halliday, Resnick, Walker - Fondamenti di Fisica - Casa Editrice Ambrosiana, 1995.
• Serway - Principi di Fisica - EdiSES, 1996.
• Duncan - Fisica per Scienze Biomediche - Casa Editrice Ambrosiana, 1994.
• Coluzza, Ferrari, Levi - Esercizi di Fisica per Biologia e Scienze Naturali - Cisu, 1988.
• Ragozzino - Problemi di Fisica con soluzione esplicita ragionata - Casa Editrice
Ambrosiana, 1993.
• Davidson - Metodi matematici per un corso introduttivo di Fisica - EdiSES, 1998.
Paolo Bagnaia - CTF - Introduzione
♠
9
Prove finali
! scritto + orale (~ 1 ogni 1.5 mesi);
! scritto :
! prenotazione in portineria;
! lo scritto annulla i precedenti;
! tre ore, possibile ritirarsi entro ~ 1 ora;
! ammissione all’orale se voto (altrimenti “N.A.”);
! (se positivo) validità > 6 mesi (vedere avviso);
! orale :
! prenotazione in portineria (foglio differente);
! se ok, verbale comune con matematica (“corso
integrato”).
Paolo Bagnaia - CTF - Introduzione
♠
10
Scritti
• tre ore;
• al Palazzo degli esami
(via Induno, vicino a viale Trastevere)
[non sempre, vedi foglio prenotazioni];
• testi “teorici” : si;
• libri o quaderni di esercizi : no;
• fogli distribuiti all’inizio :
– bella copia [unico da riconsegnare]
con 1 esercizio/facciata;
– brutta copia;
– testo.
Paolo Bagnaia - CTF - Introduzione
♠
11
Esoneri
• da tre anni, lo scritto può essere sostituito da
“compiti di esonero”;
• due compiti :
" primo compito (marzo) riservato a chi frequenta;
" prenotazioni per il primo esonero in aula;
" secondo compito (fine maggio) riservato a chi ha
superato il primo;
" esonero per chi supera il secondo compito.
• molti esercizi semplici,
• esonero valido ~ 1 anno (se no, fare lo scritto).
Paolo Bagnaia - CTF - Introduzione
♠
12
Avviso ai naviganti (su internet)
Queste presentazioni sono state espressamente create per gli studenti del primo anno
del Corso di Laurea in CTF della “Sapienza”. Nonostante ciò, la loro utilità didattica è
tutt’altro che garantita. La maggior parte dei miei colleghi docenti di Fisica, interpellati
al riguardo, hanno espresso l’opinione che questo tipo di presentazione oscura i reali
contenuti sotto la sofisticazione tecnologica e la raffinatezza formale, in analogia con
gli spot televisivi, che mascherano rozzi messaggi commerciali con delle apparenze
raffinate.
La mia opinione personale è meno negativa : penso che una tecnologia potente, in
mano ad un docente esperto e a studenti maturi, possa produrre dei buoni risultati.
Tuttavia, come in tutte le scienze sperimentali, la sola verifica possibile è nel risultato
reale, cioè nella utilità riscontrata dagli studenti.
Pertanto, tutti coloro che volessero esprimere critiche, commenti, apprezzamenti di
qualsiasi genere (oltre ovviamente segnalare errori tecnici, formali o sostanziali) sono
vivamente pregati di farmi conoscere la loro opinione. Mi si permetta di ricordare che è
molto difficile produrre della buona didattica senza una continua interazione con gli
studenti.
P.B., Roma, gennaio 2001
Paolo Bagnaia - CTF - Introduzione
♠
13
Sito web
• Sito WWW :
http://www.uniroma1.it
→ dipartimenti
→ Fisica
→ DIDATTICA
→ SERVER CON INFORMAZIONI SULLA DIDATTICA
→ FISICA PER FARMACIA
[http://www.phys.uniroma1.it/DOCS/CORSI/ChFar/bagnaia/index.html]
Paolo Bagnaia - CTF - Introduzione
♠
14
Fine Introduzione
Paolo Bagnaia - CTF - Introduzione
♠
15
La Meccanica
• Cinematica, Statica, Dinamica.
• La cinematica studia il moto dei corpi in modo
descrittivo, senza indagarne le cause.
• Cinematica = geometria analitica ⊕ evoluzione
temporale.
• Moto in una (per cominciare) e più dimensioni
• ! quanti valori per identificare la posizione di
un corpo ? Concetto di “grado di libertà”.
Paolo Bagnaia - CTF - 1a - Cinematica
♠
1
Rappresentazioni grafiche del moto
y
f(x,y) : equazione della traiettoria
(no tempo)
P(x’,y’)
x
x
x = x(t) : equazione oraria del moto
x’=x’(t’)
Differenti !!!
t
Paolo Bagnaia - CTF - 1a - Cinematica
♠
2
Velocità e accelerazione
• Per ora, solo in una dimensione.
∆x = x(t 2 ) − x(t1)
• Spostamento ∆x :
• Velocità media nel tempo t :
vM =
• Velocità istantanea al tempo t :
x(t + ∆t ) − x(t ) dx
∆x
≡
= lim
∆t →0 ∆ t
∆t →0
dt
∆t
v = lim
• Accelerazione media e istantanea :
aM =
∆x x (t 2 ) − x(t1 ) x (t1 + ∆t ) − x(t1 )
=
=
t 2 − t1
∆t
∆t
Δv v(t 2 ) − v(t 1 ) v(t 1 + Δt) − v(t 1 )
;
=
=
Δt
t 2 − t1
Δt
Δv
v(t + Δt) − v(t) dv d 2 x
a = lim
= lim
≡
≡ 2
Δt → 0 Δt
Δt → 0
Δt
dt
dt
Paolo Bagnaia - CTF - 1a - Cinematica
♠
3
interpretazione geometrica
x2
vMedia = ∆x / ∆t ∝ tan (α)
corrisponde alla pendenza
del segmento — ;
x1
se ∆t → 0 ⇒ ∆x → 0,
il triangolo diviene più
piccolo, ma α resta finito;
il segmento — approssima la
tangente alla curva — .
x
∆x
α
∆t
t1
Paolo Bagnaia - CTF - 1a - Cinematica
t2
t
corrispondenza tra i concetti
di “derivata”, “pendenza”,
“tangente”, “approssimazione
lineare”.
♠
4
Esempi :
• corpo fermo : v=0, a=0 : x-xº = v·(t-tº) = 0 ⇒ x = xº.
• moto uniforme : v=cost, a=0 :
x-xº = v (t-tº) → x = xº + v t.
• moto uniformemente accelerato :
x
a=cost ; [tº = 0].
v(t) - vº = a t → v(t) = vº + a t.
vM = [v(t) - vº] / 2 = vº + ½ a t .
x - xº = vM t
→ x = xº + vº t + ½ a t2.
t
Paolo Bagnaia - CTF - 1a - Cinematica
♠
5
moto uniformemente accelerato
x
t = - vº/a
v
a
t = - vº/a
a
xo
t
t
t
vo [ <0 !!!]
x = xº + vº t + ½ a t2;
Paolo Bagnaia - CTF - 1a - Cinematica
v = vº + a·t.
♠
6
Esempio (caduta dei gravi)
moto uniformemente accelerato
a=-g
costante di gravità
scelta del sistema di riferimento (verso l’alto)
y = yº + vº t + ½ a t2
se : vº = 0 ; a = - g
y = yº - ½ g t2
Ex. : trovare t’ per cui y(t’) = 0
yº - ½ g
t’2 =
Paolo Bagnaia - CTF - 1a - Cinematica
0
→
t' = ±
2y 0
g
y
???
t’
t
♠
7
Vettori :
molte grandezze fisiche possono
essere rappresentate da vettori
[ex. punti nello spazio, velocità, ...]
un vettore ha bisogno di 3 “numeri”
per essere definito
[ex. componenti x,y,z
- OPPURE modulo + 2 angoli]
Paolo Bagnaia - CTF - 1a - Cinematica
y
rY
O
r=r(t)
rX
x
NB :
• nel disegno, solo due
dimensioni (x,y),
aggiungere la terza (z);
• si può scrivere r
→
oppure r
♠
8
Operazioni tra vettori (1)
• somma
• differenza
→
→
→
s=a+b
→
→
→
a
→
d=a-b
→
d
→
b
→
a
→
b
→
→
+
Paolo Bagnaia - CTF - 1a - Cinematica
s
v
→
-v
♠
9
Operazioni tra vettori (2)
• prodotto “scalare”
→
→
→
→
→
s=a·b
→
• prodotto “vettoriale” v = a × b
→
c
→
a
b cos φ
→
b
Paolo Bagnaia - CTF - 1a - Cinematica
→
b
→
a
♠
10
Velocità, accelerazione → vettori
• posizione
→
→
r = r(t)
→
→
→
→
→
• spostamento
∆r = r(t2) - r(t1) = r(t1+∆t) - r(t1)
• velocità media
→
vM= ∆r / ∆t
• velocità istant.
→
v=dr / dt
[vx=dx/dt; vy=dy/dt; vz=dz/dt]
• accelerazione media
→
aM = ∆v / ∆t
• accelerazione istant.
→
Paolo Bagnaia - CTF - 1a - Cinematica
→
→
→
→
a = dv(t)/dt =
→
2
d r(t)/dt2.
♠
11
vettore posizione e velocità
y
→
→
r1
∆r
→
r2
x
• posizione r1, r2;
• spostamento ∆r.
Paolo Bagnaia - CTF - 1a - Cinematica
♠
12
Velocità e accelerazione
• la velocità istantanea è tangente alla traiettoria
(semplice conseguenza della definizione);
• viceversa, l’accelerazione non ha sempre la stessa
direzione;
• possiamo scomporla in due componenti :
" componente parallela alla velocità (accelerazione
tangenziale); modifica solo il modulo della velocità;
" componente ortogonale alla velocità (accelerazione
normale); modifica solo la direzione della velocità;
" [esempi : l’acceleratore e il volante dell’automobile]
Paolo Bagnaia - CTF - 1a - Cinematica
♠
13
Accelerazione tangenziale e normale
y
v’
v
an
a
at
traiettoria
NB
→
→
→
→
an · v = 0
→
→
at · v = a · v
xx
Paolo Bagnaia - CTF - 1a - Cinematica
♠
14
Esempio : moto dei
gravi in 2 dimensioni
Asse x
x0 = 0;
v 0x = v ⋅ cos ϑ ;
ax = 0
Asse y
y 0 = 0;
v 0y = v ⋅ sin ϑ ;
a y = −g
 x(t ) = v ⋅ cosϑ ⋅ t


1 2
 y(t ) = v ⋅ sinϑ ⋅ t − 2 gt
Paolo Bagnaia - CTF - 1a - Cinematica
t = x (v ⋅ cosϑ)
gx2
y = x ⋅ tanϑ − 2 2
2v cos ϑ
♠
15
moto dei gravi in 2 dimensioni
y
[v2 sin(2θ)/(2g),
v2 sin2θ/(2g)]
v sinθ
[0,0]
θ
v cosθ
Paolo Bagnaia - CTF - 1a - Cinematica
[v2 sin(2θ)/g,
0]
x
♠
16
Moto circolare
uniforme
ω ≡
dϑ
dt
[=velocità angolare]
 x(t ) = R ⋅ cos(ωt )

 y (t ) = R ⋅ sin(ωt )
y
 v x = −ωR ⋅ sin(ωt )
 y
 v = ωR ⋅ cos(ωt )
θ
x
a x = −ω 2 R ⋅ cos(ωt )
 y
2
a
R ⋅ sin(ωt )
=
−
ω

→
v = ωR
ω = v/R
a = ω 2R
= v2 R
2→
a = −ω r
Paolo Bagnaia - CTF - 1a - Cinematica
♠
17
Moto circolare uniforme : accelerazione
v’A
vA
α
vB
triangolo v’A vA
R
R’
→
→
→
v′A = v B 
→

v′A ⊥ R  ⇒ α = ∆ϑ
→
v B ⊥ R' 
∆θ
→
def. di accelerazione media
→
a M ⋅ ∆ t = v B − v A = 2 v sin( α 2 ) =
= 2 v sin( ∆ ϑ 2 )  
→ v ⋅ ∆ ϑ
t→0
→
a=
dϑ
⋅ v = ω ⋅ v = ω 2 R = v2 R
dt
Paolo Bagnaia - CTF - 1a - Cinematica
→
→
∆t → 0 ⇒ ∆θ → 0 ⇒ va → vb ⇒ α → 0
⇒ a → punta verso il centro.
♠
18
Le unità di misura
Unità
fondamentali :
• metro (m) : in origine 1/40 000 000 della
circonferenza terrestre → definito in
modo che c=299 792 458m/s
• secondo (s) : in origine 1/(24x60x60) del
giorno solare medio → definito dalla
frequenza della luce emessa dal Cesio
133 (1 s = T(cesio) x 9 192 631 770
• massa (Kg) : chilogrammo campione oppure in funzione delle masse atomiche
Sistema “MKS” (esiste anche il sistema “CGS”) +
unità derivate (ex. velocità : spazio / tempo → m/s
Paolo Bagnaia - CTF - 1a - Cinematica
♠
19
Unità derivate
Si definiscono nuove unità di misura, derivate
dalle unità fondamentali. Ex. :
• velocità = dx/dt → misurata in m/s;
• accelerazione = d2x/dt2 → misurata in m/s2.
Paolo Bagnaia - CTF - 1a - Cinematica
♠
20
Dimensioni delle grandezze fisiche
Tutte le grandezze fisiche sono definite a partire da poche
grandezze fondamentali.
Ex., in meccanica, sono sufficienti TRE grandezze fondamentali.
Scegliamo : L, T, M.
Conseguenza : ogni altra grandezza può essere espressa in
funzione di MLT [equazioni dimensionali ]. Ex.
[v] = [L·T-1]; [a] = [L·T-2]; [f] = [M · L · T-2].
NB : si confrontano, sommano, sottraggono solamente grandezze
omogenee, cioè con le stesse dimensioni. Ex. v1 = v2 + v3.
→
Gli argomenti di funzioni trascendenti sono “numeri puri”. Ex.
x = R · sin(ωt) ove [x] = [R] = [L], [ω] = [T-1].
Paolo Bagnaia - CTF - 1a - Cinematica
♠
21
Fine parte 1a
Paolo Bagnaia - CTF - 1a - Cinematica
♠
22
Leggi fondamentali della dinamica
[I. Newton, ~ 300 anni fa]
• Dal punto di vista della logica formale, sono postulati
da cui è possibile derivare altre leggi come teoremi.
• Sono state scelte in modo che esse, e le loro
conseguenze, siano in accordo, entro le precisioni di
misura, con le osservazioni sperimentali effettuate.
• Nel tempo, nuovi fenomeni (o migliori precisioni) →
miglioramenti successivi; le vecchie leggi sono prime
approssimazioni delle nuove (ex. relatività speciale,
meccanica quantistica).
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
1
Prima legge
“Un corpo non soggetto ad interazioni, permane nel suo stato di
quiete o di moto rettilineo uniforme.”
Sembra facile, in realtà :
! richiede la conoscenza delle interazioni, a priori dal loro effetto
sul moto dei corpi (altrimenti è un enunciato “circolare”);
! si può sempre trovare un sistema di riferimento in cui il
principio sia soddisfatto (ex. un sistema solidale con il corpo
allo studio), in modo che il principio sia banalmente valido per
tutti i corpi, soggetti ad interazioni, oppure no.
¿ come si risolve questo problema ?
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
2
Soluzione
Prima legge modificata : “Un corpo non soggetto ad interazioni
permane nel suo stato di quiete o di moto rettilineo uniforme, in
un sistema di riferimento inerziale”.
! la legge dice che il moto dei corpi si può studiare solo nei
sistemi in cui non compaiono anomalie (accelerazioni non
dovute ad interazioni);
! dato un sistema di riferimento inerziale, tutti i sistemi, in quiete
o in moto rettilineo uniforme rispetto ad esso, sono anche essi
dei sistemi di riferimento inerziali;
! dal punto di vista della dinamica, quiete e moto rettilineo
uniforme sono equivalenti.
[NB. non abbiamo fatto ricorso al concetto di “stelle fisse” (?!)]
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
3
Seconda legge
“Una forza impressa ad un corpo produce un’accelerazione
parallela alla forza e ad essa proporzionale; il coefficiente di
proporzionalità non dipende dalla forza, ma dalle proprietà
intrinseche del corpo.”
F=ma
! richiede la conoscenza delle forze, a priori dal loro effetto sul
moto dei corpi (altrimenti è un enunciato “circolare”);
! il coefficiente “m” è la massa di un corpo :
" la massa non dipende dallo stato di quiete o di moto del corpo;
" la massa si mantiene la stessa per tutta la vita di un corpo.
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
4
Le forze
• la seconda legge è la base di tutta la dinamica :
! osservando la natura, si descrivono le forze con leggi
matematiche;
! quindi, applicando la seconda legge, si calcola il moto
dei corpi [in sistemi inerziali !!! ] ;
• le forze sono additive : ex., se su un corpo si
esercitano due forze ( F1 e F2 ) la legge dice che :
m a = F1 + F2 = FTot
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
5
Unità di misura della forza
[F] = [m] · [a] = [m · l · t -2]
si misura in Newton (MKS) o in dine (CGS);
1 N = 1 Kg · 1 m / 1 s2
1 dine = 1 g · 1 cm / 1 s2 = 1 N / 105
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
6
Terza legge
“Quando un corpo A imprime una qualsiasi forza FAB su un
corpo B, automaticamente il corpo B imprime su A una forza
FBA uguale in modulo ed opposta in verso” (Principio di
azione e reazione).
FAB = - FBA
! non è particolarmente difficile : molti esempi pratici (nuoto,
barche a remi, ecc.);
! nei sistemi isolati, la somma vettoriale di tutte le forze (cioè la
forza totale) è sempre nulla, perché tutte le forze tra corpi,
comunque complicate, si cancellano due a due.
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
7
La forza peso
F = mg · g
accelerazione di gravità
[costante, = 9.8 m/s2, verso il basso]
massa (meglio, “massa gravitazionale”)
forza
" g diretta verso il basso (vedi oltre, “gravitazione”);
" mg = m per tutti i corpi; cioè la “massa” che compare nel
secondo principio è identica a quella che compare nella
espressione della forza peso (perché ???);
" conseguenza : l’accelerazione di caduta è la stessa per tutti
i corpi (a = g), ed è indipendente dalla massa.
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
8
“I vincoli”
• esempi : tavoli, rotaie, fili inestensibili, ...
• il “trucco” consiste nel sostituire il vincolo con una
forza ortogonale al vincolo, che produca lo stesso
effetto sul moto.
Ex. :
forza vincolare [=-mg]
peso [=mg]
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
9
i vincoli nel moto circolare uniforme
|a| = v2 / r
|F | = m v 2 / r
y
la forza è diretta
verso il centro
(forza centripeta)
in pratica, si può usare
un filo robusto (vincolo)
Paolo Bagnaia - CTF - 1b - Meccanica del punto
a
a
x
a
a
♠
10
Scomposizione delle forze
•
•
•
esempio classico : il piano inclinato
la forza totale (Wtot) è diretta verso il basso;
scomposizione :
" sia θ l’angolo del piano inclinato
" W · cos θ ortogonale al piano inclinato, bilanciata dalla
forza vincolare;
" W · sin θ efficace, parallela al piano inclinato.
•
cioè, lungo il piano inclinato :
m a = W sin θ = m g sin θ
l’accelerazione di gravità g è minore di un
fattore sin θ .
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
11
il piano inclinato
W cos θ
W sin θ
W = mg
θ
W cos θ
W sin θ
piano inclinato (caso senza attrito)
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
12
Forze di attrito
" due tipi di attrito :
" attrito statico (impedisce l’inizio del moto) :
• opposto alle forze che agiscono sul corpo;
• valore massimo : Fstat(max) = µs N = µs m g
(NB in modulo, la direzione è differente !!!).
" attrito dinamico (agisce durante il moto) :
• F = µd N = µd m g
• direzione e verso = - v
" i coefficienti µs e µd sono differenti (µd < µs) e dipendono
dalle superfici dei corpi e dalla presenza di lubificanti,
polveri, etc. (cioè dalla presenza di asperità che
impediscano lo scorrimento delle superfici)
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
13
il piano inclinato + attrito
FTOT
W cos θ
Fa = µ m g cos θ
W = mg
θ
W cos θ
W sin θ
piano inclinato (caso con attrito dinamico)
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
14
il lavoro
• Si definisce lavoro di una forza F su un corpo che
si sposta di un tratto d :
L = F · d = F d cos θ
F,d concordi (θ < 90°);
• L>0
se
F,d discordi
• L<0
se
(θ > 90°);
F,d ortogonali (θ = 90°).
• L=0
se
ex.
caduta di un grave da fermo (forza peso) : L = m g h;
attrito dinamico : L < 0;
attrito statico : L = 0;
moto circolare uniforme (forza centripeta) : L = 0;
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
15
Il lavoro
F
θ
L=F·d
d
F
L = F d cos θ
θ
d
F cos θ
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
16
Lavoro di forze variabili
L’espressione precedente può
essere impossibile da calcolare se
una delle grandezze in gioco varia
di modulo e/o di direzione nel
periodo considerato.
In tale caso, occorre scomporre il
tragitto in intervalli piccoli (al limite,
infinitesimi) e considerare il lavoro
totale come la somma dei lavori
infinitesimi,
corrispondenti
ai
tragitti:
∫
L=
→
→
F(x)·dx
F(x)
x
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
17
Unità di misura del Lavoro
[e di tutte le grandezze con le stesse dimensioni]
[L] = [F d] = [m l2 t- -2]
MKS : J = joule = 1 newton · 1 metro;
CGS :
erg = 1 dine · 1 centimetro = 1 J / 107.
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
18
Energia cinetica
• Un corpo, di massa m e velocità v (modulo),
possiede un’energia cinetica data da :
K = ½ m v2
• K dipende solo dal modulo della velocità, non
da direzione e verso;
• [K] = [ m v2 ] = [ m l2 t -2 ] = [ L ]
• pertanto K si misura in J (erg).
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
19
teorema dell’energia cinetica
Il lavoro totale delle forze agenti su un corpo è uguale
alla variazione di energia cinetica del corpo stesso :
y
L = ∆ K = KFIN - KINI
vFIN
FIN
traiettoria
• valido per qualsiasi forza;
• correla grandezze differenti :
! lavoro (forze, spostamenti);
! en. cinetica (massa, velocità).
vINI
INI
x
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
20
teorema dell’energia cinetica (2)
Dimostrazione (caso
unidimensionale con
accelerazione costante)
amedia = ( v - v 0 ) / ∆t;
x = x0 + v 0∆t + 1 2 ⋅ a ( ∆t )2 ;
L = F ⋅ ∆x = m ⋅ a ⋅ ∆x =
x − x0 = ∆x =
v - v0 1
= m⋅
⋅ ( v + v 0 ) ∆t =
∆t 2
1
= m ( v 2 - v 02 ) =
2
1
1
2
= mv - mv 02 .
2
2
= v 0∆t + 1 2 ⋅ ( v − v 0 ) ∆t =
Paolo Bagnaia - CTF - 1b - Meccanica del punto
= 1 2 ⋅ ( v + v 0 ) ∆t .
♠
21
teorema dell’energia cinetica (3)
x1
L = F ( x ) ⋅ dx
x0
∫
Dimostrazione (caso
unidimensionale
generale)
dv
F ( x ) ⋅ dx = m ⋅ a ⋅ dx = m ⋅ ⋅ dx =
dt
dv dx
dv
= m ⋅ ⋅ ⋅ dx = m ⋅ ⋅ v ⋅ dx = m ⋅ v ⋅ dv
dx dt
dx
L=
∫
v1
v0
Paolo Bagnaia - CTF - 1b - Meccanica del punto
1
mvdv = m( v12 − v 02 )
2
QED
♠
22
La potenza
• definizione :
il lavoro compiuto nell’unità di tempo
W = dL / dt
1 Watt = 1 W = 1 J / 1 s
(anche :
cavallo-vapore = 736 W
lavoro in watt-ora = 3600 J)
W = dL / dt = d (F · x) / dt = F · v
Paolo Bagnaia - CTF - 1b - Meccanica del punto
[ NB : se F costante ]
♠
23
Forze conservative
• una forza è conservativa se :
" in ogni ciclo chiuso L=0;
- oppure ! L in un cammino dipende solo dai punti iniziale e
finale e NON dalla traiettoria
y
B
A
x
Paolo Bagnaia - CTF - 1b - Meccanica del punto
" LAB + LBA = 0;
! LAB= -LBA.
[dimostrazione facile, da
LAB = -LBA per le proprietà
degli integrali]
♠
24
Energia potenziale
• se una forza è conservativa, si può definire una
funzione U(x), che dipende unicamente dal
punto dello spazio x, tale che [notare i “-” ] :
LAB = -∆UAB = U(xA) - U(xB) ;
U(xB) = U(xA) - ∫A F ·dx
B
• Teorema energia cinetica →
LAB = KB - KA = UA - UB ;
KB + UB = KA + UA = ETOT = costante
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
25
differenze di energia potenziale
NB L’energia potenziale non è
una
grandezza
direttamente
misurabile.
Solamente
le
differenze di e.p. hanno rilevanza
in fisica (v. pag. prec.). La scelta
del punto di riferimento, rispetto a
cui si calcola l’e.p., si cancella
nelle differenze.
U(x0)=0
e.g. due scelte :
U*(x1)=0.
oppure
U(xA)-U(xB) = LAB = LA0 + L0B =
= LA1 + L1B = U*(xA)-U*(xB)
Paolo Bagnaia - CTF - 1b - Meccanica del punto
y
B
P0
P1
A
x
♠
26
Conservazione dell’energia
y
solo forze conservative
B
A
x
KB + UB = KA + UA = ETOT = cost.
Paolo Bagnaia - CTF - 1b - Meccanica del punto
ETOT è la
stessa nei vari
punti del
percorso !!!
♠
27
forze conservative : gravità
A
Gravità :
Ex.
oppure
U(x) = U(xo) - L
= U(xo) - m g h
= - m g h + costante
K(xA) = 0;
U(xA) = 0;
U(xB) = -mgh;
K(xB) = ½ m vB2 = ?
→ 0 = -mgh + ½ m vB2 → vB = (2gh)½
U(xB) = 0;
U(xA) = +mgh;
→ 0 + mgh = 0 + ½ m vB2
(!!!!)
→ vB = (2gh)½
Paolo Bagnaia - CTF - 1b - Meccanica del punto
B
♠
28
forze conservative : molla
Forze elastiche (ex. molla) :
F = - Kx
• la forza è proporzionale alla deformazione della molla;
• la costante di proporzionalità K indica la “robustezza” della
molla (= forza per deformazione unitaria);
• la forza è diretta lungo l’asse della molla, in senso opposto alla
deformazione;
• la forza è conservativa (facile : immaginare un ciclo).
U(x) = - L = - ∫dx (-Kx) = ½ K x2 + costante.
½ m v2 + ½ K x2 = costante.
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
29
forze elastiche
x1
F1
x2 = 0
F2 = 0
x3
F3
0
Paolo Bagnaia - CTF - 1b - Meccanica del punto
x
♠
30
forze elastiche : energia
x1
F1
1→0

6→0
—
x2 = 0
2 0→
F2 = 0

—
5 0←
—
x3
3←0
F3

—
0
Paolo Bagnaia - CTF - 1b - Meccanica del punto
x
a v U K


—
4←0

—
a v U K
♠
31
Oscillazioni - moto armonico
Ex. molla (v. indietro) :
F = - K x;
U = ½ K x 2;
" la forza riporta il corpo nel punto di equilibrio (segno “-”)
→ oscillazioni, moto periodico;
" ricordiamo il moto circolare uniforme (a = - ωr);
" proiettiamo su un asse (ex. x) - moto “armonico” :
! x = A sin (ωt);
! v = dx/dt = Aω cos (ωt);
! a = dv/dt = d2x/dt2 = -Aω2 sin (ωt);
→ F = - Kx = - KA sin (ωt) = ma = - m A ω2 sin (ωt);
→ ω = (K / m)½; T = 2π / ω = 2π (m / K)½;
" le oscillazioni sono “isocrone” (ω e T non dipendono da A)
→ oscillazioni più ampie sono compiute a velocità maggiore;
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
32
moto armonico
y
proiettare il moto
circolare uniforme
sull’asse x
x
x
x
x(t) = A sin (ωt + φ)
T = 2π / ω
A
t
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
33
moto armonico : energia
UK
x
[ω = (K / m)½]
E = ½Kx2 + ½mv2 =
= ½K[Asin(ωt + φ)]2 + ½m[Aωcos(ωt + φ)]2 =
= ½KA2 = ½mA2 ω2 = costante
x,v
Aω
A
t
x(t) = A sin (ωt + φ)
v(t) = A ω cos (ωt + φ)
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
34
forze conservative : pendolo
Fpeso = m g (verso il basso)
Ffilo = (vincolo lungo il filo)
tutte le forze sono conservative.
L
U = m g h = m g L (1 - cos θ)
m
θ
h = L (1-cos θ)
anche : proiettare le forze lungo assi (parallelo e ortogonale al filo) :
FPAR = mg cos θ + T = 0
FORT = - mg sin θ ≈ - mg θ
(“-” indica la direzione verso
il punto di equilibrio)
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
35
equazione del pendolo
Pendolo, caso di “piccole oscillazioni” :
x ≈ L θ;
F = - m g sin θ ≈ - mg θ = - mg x / L ;
" formalmente identico alla molla, con K = mg / L
→ oscillazioni isocrone; frequenza, periodo :
!
ω [= (K / m)½] = (g / L)½;
!
T = 2π / ω = 2π (L / g)½;
" moto armonico, di equazione
x = A sin (ωt);
A = xMAX = L θMAX.
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
36
pendolo
θ
L
m
mg cos θ
h = L (1-cos θ)
θ
mg sin θ
mg
Paolo Bagnaia - CTF - 1b - Meccanica del punto
FPAR = mg cos θ + T = 0
FORT = - mg sin θ ≈ - mg θ
♠
37
Forze non conservative
Ex. attrito :
• il lavoro dipende dal cammino (a
parità di coefficiente µ, maggiore
percorso = maggiore lavoro);
• la forza NON è conservativa (ex.
il lavoro in un ciclo chiuso NON è
nullo).
y
LAB > L’AB
B
A
x
L’energia si disperde nell’ambiente,
e.g. sotto forma di calore.
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
38
Fine parte 1b
Paolo Bagnaia - CTF - 1b - Meccanica del punto
♠
39
Sistemi di punti materiali
• n punti materiali di massa mi e posizione ri
(i = 1,2,3,...,N);
definizione di centro di massa :
mi ri m r + m r + m r + ...
∑
=
=
m + m + m + ...
∑mi
→
→
rcm
→
→
→
1 1
2 2
3 3
1
→
2
3
MTOTrCM = Σ miri;
MTOTvCM = Σ mivi;
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
.... segue ...
♠
1
Sistemi di punti materiali (2)
... segue ...
→ MTOTrCM = Σ miri;
Principio di azione
e reazione
MTOTvCM = Σ mivi;
MTOTaCM = Σ miai = Σ fiTOT = Σ fiEXT + Σ fiINT
=0
Teorema del centro di massa : il moto (virtuale) del c.m. è
deteminato dalle sole forze esterne al sistema; le forze interne
determinano i moti relativi dei membri del sistema :
MTOTaCM = Σ fiEXT = FTOTEXT
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
2
quantità di moto
definizione : p = m v
→ F [= ma = m dv/dt = d (mv) / dt ] = dp / dt
[spesso citata come espressione corretta della 2ª legge,
include i sistemi a massa variabile, per cui dm/dt ≠ 0].
Nei sistemi a molti punti, definiamo :
P = Σ pi = Σ mivi = MTOT vCM
Possiamo scrivere il teorema del centro di massa :
FTOTEXT = dP / dt
FTOTEXT=0 → dP / dt = 0
→ P = Σ mivi = costante
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
3
Urti
! l’urto avviene in un tempo piccolo (qualche ms);
! pertanto, le forze d’urto sono molto intense;
! pertanto, durante l’urto, possiamo trascurare le altre forze (ex.
gravità, forze elastiche, attriti);
! poiché le forze d’urto sono interne al sistema di corpi che
collidono e le forze esterne sono trascurabili, durante l’urto si
conserva sempre la quantità di moto totale dei corpi che si
urtano [→ P(prima) = P(dopo) ];
! se le forze d’urto sono conservative, poiché l’energia potenziale
prima e dopo l’urto è la stessa (forze d’urto nulle fuori della
collisione), anche l’energia cinetica si conserva durante l’urto
[ → K(prima) = K(dopo) ].
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
4
urti elastici (1)
! si chiamano u.e. quelli in cui si conserva l’energia cinetica;
! la quantità di moto si conserva comunque (vedi sopra);
! studiamo il caso (semplice) in cui le forze d’urto sono collineari
con la linea che congiunge i CM dei corpi che si urtano (urti
“centrali”, cfr. due palle da biliardo che si “spizzano”);
! semplifichiamo al caso in cui le velocità dei corpi prima dell’urto
siano parallele (urti unidimensionali);
! abbiamo quindi (in una sola dimensione) le seguenti variabili :
• masse (M, m);
• velocità prima dell’urto (V, v) e dopo l’urto (W, w);
! ... e le seguenti equazioni :
" conservazione della quantità di moto (in una dimensione);
" conservazione dell’energia cinetica.
... segue ...
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
5
urti elastici (2)
→
M
→
V
v
M
W
crash !!!
m
→
prima dell’urto
m
→
M
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
m
w
→
→
w? W?
♠
6
urti elastici (3)
p
MV + mv = MW + mw
½MV2
+
½mv2
=
½MW2
+
½mw2
E
} equazioni iniziali
m (v - w) = M (W - V)
algebra →
m (v - w) (v + w) = M (W - V) (W + V)
v+w=W+V→W=v+w-V
m (v - w) = M (v + w - V - V)
← algebra
w (m + M) = mv - Mv + 2MV
soluzioni →
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
w = [ 2MV + v (m - M) ] / (M + m)
W = [ 2mv + V (M - m) ] / (M + m)
♠
7
urti elastici (4)
Casi particolari :
soluzioni
w = [ 2MV + v (m - M) ] / (M + m)
W = [ 2mv + V (M - m) ] / (M + m)
! M=m → w = V, W = v (inversione);
! M>>m, V=0 → w = - v; W ≈ 0 (rimbalzo).
Leggi della riflessione (conseguenza) :
1. l’angolo di incidenza θ e quello di
riflessione θ’ sono uguali;
2. la traiettoria incidente, quella riflessa e
la normale al piano di riflessione
giacciono nello stesso piano.
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
θ θ’
♠
8
urti anelastici (1)
! l’energia cinetica NON si conserva [forze non conservative];
! la quantità di moto si conserva [sistema isolato] ;
! studiamo solamente il caso estremo :
i due corpi restano attaccati dopo l’urto.
MV + mv = (M + m) w
w = (MV + mv) / (M + m)
l’energia cinetica diminuisce
(si disperde, ex. in calore o
deformazioni)
∆K = KFIN - KINI = ½ (M+m) w2 - ½ MV2 - ½ mv2 =
= - ½ mM (V - v)2 / (M + m) < 0
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
9
urti anelastici (2)
→
M
→
V
v
M
m
prima dell’urto
m
crash !!!
→
M+m
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
w
→
w?
♠
10
momento delle forze
• si definisce momento di un vettore v rispetto a un
punto P :
→
r
m=r∧v
P
×
m (verso
il basso)
→
v
• il momento è correlato con il concetto di rotazione
attorno ad un asse;
• definiamo il momento della forza τ :
τ=r∧f
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
11
Equilibrio dei corpi
• i corpi puntiformi in quiete sono in equilibrio se
fTOT = Σi fi = 0
• i corpi estesi richiedono in più :
τTOT = Σi τi = Σi ri ∧ fi = 0
f1
Ex., fTOT = 0, τTOT≠ 0,
il corpo ruota :
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
f2
♠
12
Tipi di equilibrio
! stabile, se il corpo, allontanato
dalla posizione di equilibrio, vi
torna;
! instabile, se si allontana
ulteriormente;
! indifferente, se resta nella
nuova posizione;
Attenzione in più dimensioni,
ex. un “punto di sella”.
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
13
Forza di gravitazione
• le masse (gravitazionali) si attraggono :
Gm1m2
;
F=
2
r12
G = 6.67 × 10
F
m1
−11
F
m / kg ⋅ s
3
2
m2
stesso modulo, stessa direzione,
verso opposto !!! (3 principio)
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
14
Gravità e forza peso
• se r12 ≈ rterra, m1 ≈ mterra
→
F = [GmT/rT2] × m = m g
cioè la forza peso mg è solo un caso particolare della
forza di gravità, g dipende solo da mT e rT;
• la forza di gravità è conservativa (facile da dimostrare);
• l’energia potenziale vale :
U(r12) = - G m1m2 / r12 + cost
[dimostrare per esercizio :
U(r12) partendo da F;
U(r12) ≈ mgh, se sulla superficie della terra]
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
15
Le leggi di Keplero
1. i pianeti percorrono orbite ellittiche; il sole occupa uno dei
fuochi dell’ellisse;
2. il raggio vettore tra sole e pianeta spazza aree uguali in
tempi uguali;
3. il rapporto tra il quadrato del periodo e il cubo del
semiasse maggiore è lo stesso per tutti i pianeti.
NB :
"
le leggi sono “dimostrabili” a partire dalla gravità;
"
valgono per qualsiasi sistema gravitazionale, il sistema solare è solo
un esempio;
"
approssimazione m(sole) >> m(pianeti).
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
16
1ª legge di Keplero
ellisse : (x/a)2 + (y/b)2 = 1
(generalizzazione del cerchio, a = b = R).
" a, b = semiassi (maggiore, minore);
" comete periodiche : ellissi schiacciate;
" altri corpi celesti : ellissi oppure
iperboli, parabole
y
x
sole
pianeta
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
NB : è un’esagerazione, le
orbite reali dei pianeti sono
quasi cerchi.
♠
17
ellisse
" ellisse : (x/a)2 + (y/b)2 = 1;
" s1 + s2 = d1 + d2 = cost.
" f1, f2 fuochi.
y
b
s1
d1
f1
s2
f2
d2
x
a
! il cerchio è un caso particolare con a = b = s1 = s2 = d1 = d2 = R.
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
18
2ª legge di Keplero
• i due triangoli (! e !) corrispondono a tempi uguali,
ed hanno area uguale; pertanto :
∆ A = ½ × r × r θ = ½ r2 ω δt = costante
→ ω r2 = v r = costante → v ∼ 1 / r
y
r,θ
r’,θ’
sole
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
x
♠
19
3ª legge di Keplero
dati due pianeti :
T2 / a3 = T’2 / a’3
Dim. (caso particolare,
orbite circolari):
m1 ω12 r1 = m1 [2π/T1]2 r1 =
= G ms m1 / r12
a
→ T12 / r13 = 4 π2 / [G ms]
analogamente :
a’
sole
T22 / r23 = 4 π2 / [G ms]
pertanto :
T12 / r13 = T22 / r23 = costante
(indipendente dal pianeta)
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
20
Fine parte 1c
Paolo Bagnaia - CTF - 1c - Meccanica dei sistemi
♠
21
Meccanica dei fluidi
! definizioni;
! statica dei fluidi (principio di Archimede);
! dinamica dei fluidi (teorema di Bernoulli).
[importanti applicazioni in biologia / farmacia : ex. circolazione del sangue]
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
1
Definizioni
• fluido = sostanza che può scorrere, ed assumere la forma
(=liquido) o le dimensioni (=gas) del contenitore;
• densità
: ρ = dm / dV (= massa / volume, in Kg/m3, g/cm3);
• pressione : p = dF / dA (=forza/ area, in N/m3 = pascal, dine/cm3) [*];
• viscosità
: F = η A v / s (forza “di taglio” tra superfici, vedi oltre).
[*] p non è un vettore, la pressione è isotropa (= la stessa in tutte le direzioni,
vedi il principio di Pascal).
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
2
Viscosità
→
→
v
F
A
→
s
F
v=0
F=ηAv/s:
" A = area di due lamine di liquido, poste a distanza s;
" v = velocità relativa delle lamine;
" η = coefficiente di viscosità del liquido (funzione anche di
temperatura, pressione);
" F = forza di viscosità (due forze uguali ed opposte sulle due lamine).
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
3
Principio di Pascal
Un cambiamento di pressione in un fluido è trasmesso
inalterato a tutte le porzioni del fluido ed alle pareti
(→ la pressione è isotropa).
→
F
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
p
♠
4
Statica dei fluidi
patm= po
0
1
2
y
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
[il liquido è a riposo]
! F2 = F1 + mg = F1 + ρVg;
! p2 = F2 / A = F1 / A + ρVg / A =
= p1 + ρg (y2 - y1);
! y1 → 0; y2 - y1 = h; p1 = po = patm;
! p = po + ρgh.
la pressione aumenta
linearmente con la profondità.
♠
5
vasi comunicanti
po
po
po
po
po
stessa
altezza
p1
p2
p1=p2
il liquido è in quiete → p1 = p2;
→ h1 = h2 → il liquido è alla stessa altezza in tutti i vasi;
[NB : è necessario che tutta la superficie del liquido sia a pressione po]
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
6
Il barometro
• patm + ρgh1 = p=0 + ρg(h1+h2);
vuoto
p=0
• patm = ρ g h2 ;
h2
l’altezza della colonna di liquido (mercurio)
non dipende né dalla forma dei tubi, né
dall’altezza h1, ma solo dalla densità ρ e
dalla pressione atmosferica patm. Si può
misurare patm in mm-Hg ( = h2).
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
patm
ρ
h1
♠
7
La pressa idraulica
→
F1
S1
p1
S2
→
F2
p1 = F1 / S1 = p2 = F2 / S2;
F2 = F1 × S2 / S1 >> F1;
p2
È un moltiplicatore di forza
(una “leva idraulica”)
" lavoro, per spostamenti d1 e d2 (= d1 × S1 / S2) :
L2 = F2 × d2 = [F1 × S2 / S1] × [d1 × S1 / S2] = F1 × d1 = L1.
[le forze sono conservative → l’energia meccanica si conserva
→ il lavoro speso sul pistone 1 viene integralmente restituito sul pistone 2]
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
8
Principio di Archimede
" cubetto, di lato d, parallelo alla verticale;
" 6 forze, dovute alla pressione, sui lati;
→
F1
→
p1
F2
p2
" 4 forze (due coppie) si annullano;
" restano F1 = p1×d 2 e F2 = p2×d 2;
" FTOT = F1 - F2 = (p1 - p2) × d 2;
FTOT = (p1 - p2) × d2 = ρliquido g d × d 2 = Vcorpo ρliquido g = mliquido g;
“la forza di Archimede è pari alla forza peso del liquido spostato,
ed è diretta verso l’alto”
la forza totale sul corpo è
FArch + Fpeso = (mliquido - mcorpo) g = (ρliquido - ρcorpo) V g
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
[→ navi, etc.]
♠
9
fluido ideale
in fluidodinamica si definisce il “fluido ideale” :
! incompressibile (i.e. ρ è costante, indipendente da p,
v, T, h, ...);
! viscosità nulla (η = 0, lavoro di scorrimento nullo);
! moto non rotazionale (cfr. i vortici nei fiumi);
! moto “laminare” (= le traiettorie delle molecole del
fluido sono linee che non si chiudono e non variano
nel tempo).
Concetto di “tubo di flusso” :
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
10
Dinamica dei fluidi
S2
→
v
S1
tubo di flusso
nel tempo ∆t, dati due volumi uguali, di area ⊥ S1 e S2 :
• attraverso S1 : m1 = ρ V1 = ρ d1 S1 = ρ1 v1 ∆t S1;
• attraverso S2 : m2 = ρ V2 = ρ d2 S2 = ρ2 v2 ∆t S2;
• ρ1 = ρ2 → m1 = m2 → v1 S1 = v2 S2;
→ portata Q = dV / dt [= v1 S1 = v2 S2 ] = costante.
NB : v ∼ 1 / S (!!!), cfr. le automobili in autostrada ! quale è la differenza ?
Soluzione : ρ ≠ costante
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
11
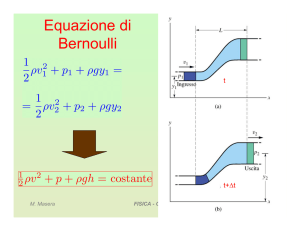
legge di Bernoulli (1)
S2,v2,
h2,p2
→
v
S1,v1,h1,p1
tubo di flusso
" esprime la conservazione dell’energia nel moto dei fluidi;
" calcoliamo variazione di energia cinetica, lavoro della
gravità, lavoro delle forze di pressione tra i punti 2 e 1, per
una piccola massa m, che occupa un volume V (m = ρ V) :
! ∆K = K2 - K1 = ½ m v22 - ½ m v12 = ½ ρ V (v22 - v12);
! ∆LG = L12,G = - mg (h2 - h1);
! ∆LP = L2,P - L1,P = - (p2 S2 δ2 - p1 S1 δ1) = - (p2 - p1) V;
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
12
legge di Bernoulli (2)
spiegazione dei termini :
S2,v2,
h2,p2
→
v
S1,v1,h1,p1
tubo di flusso
δ
→
S
v
h = quota (→ energia
potenziale);
p = pressione;
v = velocità;
S δ = V = m / ρ.
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
13
legge di Bernoulli (3)
S2,v2,
h2,p2
→
v
S1,v1,h1,p1
tubo di flusso
" teorema dell’energia cinetica : ∆K = ∆LG + ∆LP →
½ ρ V (v22 - v12) = - m g (h2 - h1) - (p2 - p1) V; [ dividere / V ]
½ ρ (v22 - v12) = - ρ g (h2 - h1) - (p2 - p1);
[riarrangiare i termini]
½ ρ v22 + ρ g h2 + p2 = ½ ρ v12 + ρ g h1 + p1;
[i due punti sono generici]
½ ρ v2 + ρ g h + p = costante;
NB : “costante” → la somma dei tre termini è la stessa, se calcolata in tutti i
punti del tubo di flusso; inoltre, non varia nel tempo.
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
14
Fine parte 2
Paolo Bagnaia - CTF - 2 - Meccanica dei Fluidi
♠
15
Fenomeni termici
•
•
•
•
•
•
•
•
•
•
•
calore e temperatura;
dilatazione termica;
calorimetria;
passaggi di calore;
cambiamenti di fase;
1° principio della termodinamica;
trasformazioni termodinamiche;
i gas perfetti;
2° principio della termodinamica;
il ciclo di Carnot;
l’entropia.
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
1
Calore e temperatura
!attenzione : calore ≠ temperatura !!!
[molti esempi : stufe e cerini, ...]
! termometro : misura della temperatura;
! principio 0 della termodinamica : “due corpi, in
equilibrio termico con un terzo, sono in equilibrio tra
loro” [NB equilibrio termico = stessa temperatura];
! definizione di temperatura (poi, meglio) :
• 0° = ghiaccio fondente (a pressione atmosferica);
• 100° = acqua bollente
(”
”
”
);
! termometro a gas (scala assoluta, vedi oltre).
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
2
dilatazione termica
dato empirico : T aumenta → i corpi si dilatano
[modellini microscopici].
a) dilatazione lineare, parametro “α” (in gradi C-1) :
∆L = L α ∆T;
α = (∆L / L) (1/ ∆T );
∆L
-5
-6
-1
α ≈ 10 ÷ 10 C
b) dilatazione di volume, parametro “β” :
∆V = V β ∆T ;
β = (∆V / V ) (1/ ∆ T );
β ≈ 3 α.
[... segue ...]
Paolo Bagnaia - CTF - 3 - Termodinamica
T
T+∆T
♠
3
calcolo della dilatazione termica
∆V / V = (V’ - V) / V =
T
= [(L + ∆L)3 - L3] / L3 =
=
[L3
+
3L2 ∆L
+ ... - L3) / L3 =
∆L
T+∆T
≈ 3L2 ∆L / L3 = 3 ∆L / L.
β = (∆V / V) (1/ ∆T ) =
≈ 3 (∆L / L) (1/ ∆T ) =
= 3 α.
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
4
il calore
" il calore è l’energia che si trasferisce da un
corpo all’altro, a causa delle differenze di
temperatura;
" pertanto, si misura in J (= joule);
" altra unità (obsoleta) : caloria (= calore
necessario per innalzare di 1 C la massa di 1
g di acqua);
" conversione :
! 1 Joule = 0.2389 calorie;
! 1 caloria = 4.186 Joule
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
5
calorimetria
! descrive i trasferimenti di calore, senza studiarne le
cause [analogia : cinematica];
! definizioni :
• capacità termica C di un corpo : calore necessario ad innalzare di
un grado la temperatura del corpo [per una trasformazione
generica : Q = C ∆T ];
• calore specifico c di una sostanza : calore necessario ad
innalzare di un grado la temperatura di un grammo della sostanza
[per una trasformazione generica : Q = m c ∆T, C = m c ];
• calore specifico “molare” cm di una sostanza (gas) : calore
necessario ad innalzare di un grado la temperatura di una mole*
della sostanza [per una trasformazione generica : Q = nm cm ∆T,
C = nm cm ].
[*] 1 mole : NA molecole; NA = numero di Avogadro = 6.02 × 1023.
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
6
passaggi di calore
il calore va “spontaneamente”
dal corpo più freddo a quello
più caldo, fino a che la
temperatura dei due corpi non
diventa la stessa.
Q(1→2)  = Q(2→1);
m1 c1 Tf - T1 = m2 c2 Tf - T2 ;
T1
Q→
T2
T1 > T2
↓
Tf
m1 c1 (T1 - Tf )= m2 c2 (Tf - T2 ).
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
7
cambiamenti di fase
per certi valori critici dei parametri della
materia (ex. ghiaccio a 0° a pressione atmosferica),
una immissione di calore non provoca
aumento di temperatura, ma un cambio
di “fase” (stato di aggregazione della
materia (ex. da solido a liquido) );
“calore latente” L = quantità di calore
necessaria per il cambiamento di fase di
una quantità unitaria di massa del
materiale (ex. L[acqua↔ghiaccio] = 333 KJ / Kg) :
m
↓Q=Lm
Q = L m.
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
8
trasmissione del calore : conduzione
• passaggio del calore tra due corpi a contatto (a livello
microscopico : piccoli urti tra molecole contigue);
• legge della conduzione :
H = dQ/dt = k A (T1 - T2) / L
L
k=
A
T1
T2
Paolo Bagnaia - CTF - 3 - Termodinamica
coefficiente di conduzione, dipende
dal materiale :
# metalli : k grande, 10÷500 W / (m K);
# isolanti termici : k piccolo, .01÷1 W / (m K).
♠
9
trasmissione del calore : convezione
• il liquido, scaldandosi, si
dilata → diviene meno
denso → risale per il
principio di Archimede;
→ in alto fluido caldo, in
basso fluido freddo;
• molto comune in natura
(pentole
di
cucina,
atmosfera terrestre, ...);
NB : la gravità gioca un
ruolo : scaldare dal basso
o dall’alto è differente !
Paolo Bagnaia - CTF - 3 - Termodinamica
discesa
principio di
Archimede
espansione
♠
10
trasmissione del calore : irraggiamento
• le onde elettromagnetiche (v. oltre) trasportano energia, in
assenza di materiali intermedi;
• la potenza irraggiata è data dalla legge di Stefan-Boltzmann :
Wirr = ε σ A T4.
emittanza della
superficie ( ≤ 1 )
costante di S.-B.
(5.67×10-8W/m2K4)
Paolo Bagnaia - CTF - 3 - Termodinamica
temperatura
(Kelvin, vedi)
A
area del corpo
(m2)
♠
11
termodinamica
Concetti fondamentali (vedi libro di testo) :
# stati micro-scopici e macro-scopici;
# parametri micro- e macro-scopici;
# equilibrio termodinamico;
# trasformazioni termodinamiche;
# trasformazioni reversibili (e non-reversibili);
# variabili di stato (ex. p V T U S );
# variabili definite dalla trasformazione (ex. L Q );
# equazioni (= leggi) di stato;
# principi della termodinamica (leggi delle trasformazioni).
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
12
Lavoro in una trasformazione
dL = F · ds = (pA) ds = p dV ;
L = ∫ p dV;
[NB p è la pressione esterna]
dV
p
→
F
L’ ≠ L
2
1
NB : in questo esempio, L > 0
Paolo Bagnaia - CTF - 3 - Termodinamica
V
♠
13
precisazione : calore e lavoro
secondo le nostre convenzioni :
# L = + ∫ p dV
[ L > 0 se il volume aumenta ];
[L<0 ” ”
”
diminuisce ].
# Q > 0 se il sistema (ex. gas) assorbe calore;
Q < 0 se il sistema (ex. gas)
cede calore;
NB in letteratura, altre convenzioni :
Q ↔ - Q; L ↔ - L
Paolo Bagnaia - CTF - 3 - Termodinamica
controllate bene
il vostro testo !!!
♠
14
esperimento di Joule
• i processi termodinamici, in cui il
lavoro si trasforma in calore, non
sono conservativi : L non si
trasforma in energia potenziale
meccanica,
ma
“scompare”
dando origine a calore;
• equivalenza calore ↔ lavoro
→
(Joule);
• il lavoro non si “conserva”; forse
la somma algebrica di calore e
lavoro è una quantità che si
conserva ...
Paolo Bagnaia - CTF - 3 - Termodinamica
1 caloria = 4.186 Joule
♠
15
1º principio della termodinamica
• separatamente, Q e L dipendono dalla trasformazione
(cioè non sono variabili di stato);
• si osserva sperimentalmente che la differenza “Q - L” è
una variabile di stato (= per tutte le trasformazioni con
gli stessi stati iniziale e finale, “Q - L” è lo stesso);
• si definisce ∆U (= variazione di “energia interna”) la
→ U è una variabile di stato);
differenza “Q - L” (→
• 1º principio della termodinamica :
∆U = Q - L
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
16
1º principio della termodinamica : commenti
• 1º principio della termodinamica : ∆U = Q - L ;
• l’enunciato precedente è corretto, ma può indurre in
errore : ∆U, Q, L non sono grandezze fisiche definite
operativamente, tra cui il principio stabilisce una
relazione [cfr. ad ex. “pV = nRT”];
• il significato fisico del principio è invece che la
differenza “Q - L” è una variabile di stato (cioè è la
stessa per tutte le trasformazioni con gli stessi stati
iniziale e finale).
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
17
Trasformazioni adiabatiche, isocore, isobare,
isoterme, cicliche, libere
! adiabatiche : senza scambi di calore con l’esterno
(Q=0 → ∆U = - L);
! isocore : senza cambiamenti di volume della sostanza
(∆V = 0 → L = 0 → ∆U = Q);
! isobare : senza cambiamenti di pressione sulla
sostanza (L = p ∆V → ∆U = Q - p ∆V );
! isoterme : a temperatura costante (dipende dalla
sostanza, ex. gas perfetto → ∆U = 0 → Q = L );
! cicliche : stato finale = stato iniziale (∆U = 0 → Q = L );
! libere (espansione libera) : p = 0 ; Q = L = 0 (∆U = 0).
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
18
grafici di trasformazioni adiabatiche, isocore,
isobare, isoterme, cicliche, libere
p
adiabatica
ciclica
isocora
isoterma
isobara
Esempi di trasformazioni
libera *
V
NB * solamente stati di equilibrio (e pertanto trasformazioni che si discostano
“poco” dall’equilibrio [ reversibili ] ) possono essere disegnate sul piano p-V.
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
19
il “gas perfetto”
• semplice sistema termodinamico, su
cui è facile ragionare;
• buona approssimazione per gas reali
rarefatti e ad alta temperatura;
• caratteristiche :
! numero molecole grande (~ NA);
! volume (gas) >> volume (proprio);
! urti elastici tra molecole e con pareti;
! uniche forze presenti : collisioni (tra
molecole + pareti);
• in pratica : p piccola, ρ piccola, T grande.
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
20
Equazione di stato dei gas perfetti
• equazione verificata sperimentalmente :
•
•
•
•
•
pV=nRT
p : pressione del gas;
V : volume occupato;
n : numero di moli (= nmolecole / NA, oppure m / mmolare);
R = 8.31 J / (mol K), costante dei gas perfetti (la
stessa per tutti i gas);
T = temperatura in gradi Kelvin (= C + 273.16°).
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
21
Trasformazioni isoterme dei gas perfetti
• isoterme a T = T * :
pV = nRT* → L = ∫ p dV = nRT*
∫ dV/V = nRT* ln (VF / VI);
p
T3
T1 < T2 < T3
T2
T1
NB isoterme reversibili
Paolo Bagnaia - CTF - 3 - Termodinamica
V
♠
22
teoria cinetica dei gas (1)
# modello di gas perfetto con una scatola a forma di cubo, di lato
d, una sola molecola di massa m e velocità v, parallela (caso a)
alle pareti della scatola;
(a)
# urti molecola-pareti elastici, mscatola >> m ;
→
m v
# variazione di quantità di moto nell’urto :
d
∆q = m vprima - m vdopo = 2 m v ;
# pertanto, la forza media su ogni faccia è :
Famedia = ∆q / t2d = 2 m v / [ 2 d / v ] = m v2 / d ;
# caso b : v con direzione qualsiasi;
# in media, dal teorema di Pitagora :
→
m v
(b)
d
<vx2> = <vy2> = <vz2> = <v2> / 3;
segue ...
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
23
teoria cinetica dei gas (2)
→
m v
# pertanto, in media :
Fbmedia = m <vx2> / d = m <v2> / ( 3 d ) ;
# consideriamo ora il caso di N molecole :
(b)
d
[ n ≡ nmoli ; M ≡ mmole ; N = n NA ; N m = mTOT = n M ] ;
FTOT = Σi Fbi = N m <v2> / ( 3 d ) = n M <v2> / ( 3 d );
# pressione su una faccia (principio di Pascal : pFACCIA = pGAS ≡ p ) :
p = FTOT / S = n M <v2> / ( 3 d 3 ) = n M <v2> / ( 3 V ) = ρ <v2> / 3;
# “velocità quadratica media” = √<v2> :
v2
=
3 pV
nM
Paolo Bagnaia - CTF - 3 - Termodinamica
=
3 RT
M
♠
24
teoria cinetica dei gas (3)
v =
2
3pV 3RT
=
nM
M
≡ distribuzione
di Maxwell
di molecole
con
# fƒ(T)
i ≡ numero
delle velocità
;
vi → f(calcolabile)
velocità
i = fi(T );
#
∫Σƒ(T
) ==Σ∫i ƒ(T
fi (T22)) dv
= N;
= N;
1) 1dv
i fi (T
più più
probabile;
[fi] = vel.
= vel.
probabile;
# v1 ≡ max [ƒ(T)]
dN/dv
T2 > T1
N vel.
ƒ(T)
/ N/ =
= vel.
media;
media;
# v2 ≡ ∫Σ
i fi vvi dv
√<v22>>==vel.
vel.quadratica
quadraticamedia
media;;
## vv33 ≡≡√<v
<v2> = Σi fi vi2 / N .
<v2> = ƒ(T) v2 dv / N .
∫
T1
v1 v2 v3
Paolo Bagnaia - CTF - 3 - Termodinamica
v
♠
25
teoria cinetica dei gas (4)
# per gas reali a T ambiente (controllare) :
√<v2> ≈ 100 ÷ 1000 m/s;
# per un gas perfetto monoatomico :
3pV 3RT
=
v =
nM
M
2
U = Σi ½ mi vi2 = ½ m Σi vi2 × N / N = ½ N m × √<v2> =
=½Nm×3RT/M=3nRT/2;
# cioè U (= energia interna) è solo funzione di T (= temperatura)
[ questo risultato è vero per tutti i gas perfetti, anche non monoatomici ] ;
! curiosità : distribuzione di Maxwell f(v) :
3/2
2

Mv
−
 M 
2

f(v) = 4π 
 v exp

RT
2
 2πRT 


Paolo Bagnaia - CTF - 3 - Termodinamica
f
T
v
♠
26
calori specifici dei gas perfetti (1)
# definizione di calore specifico molare : cx = Q / ( n ∆T ) ;
# [differente dal calore specifico “di massa”, più usato per solidi e
liquidi : c = Q / ( m ∆T ) ] ;
# problema : a parità di ∆T, Q (e quindi c) dipendono dalla
trasformazione che porta il gas da T a T+∆T ;
# l’indice “x” in cx indica la trasformazione prescelta;
# i calori specifici più comunemente studiati sono :
# cp (a “pressione costante”);
p
# cv (a “volume costante”).
cp T +∆T
cv
T
V
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
27
calori specifici dei gas perfetti (2)
# isocora ( cv ) :
! L = 0 → ∆U = Q = n cv ∆T → cv = ∆U / ( n ∆T ) ;
! monoatomico : U = 3 n R T / 2 → ∆U = 3 n R ∆T / 2 ;
cvmono = ∆U / ( n ∆T ) = cvmono = 3 R / 2 ;
# isobara ( cp ) :
p
! L = p (VF - VI) = n R (TF - TI) = n R ∆T
→ ∆U = Q - L = n cp ∆T - n R ∆T ;
! U = U(T) → ∆Uv = ∆Up
→ n cv ∆T = n cp ∆T - n R ∆T
→ cp - cv = R ;
! monoatomico :
cpmono = cvmono + R = cpmono = 5 R / 2 .
Paolo Bagnaia - CTF - 3 - Termodinamica
cp
T +∆T
cv
T
V
♠
28
calori specifici dei gas perfetti (3)
tabella riassuntiva per cv , cp , γ :
p
cp
T +∆T
cv
T
V
Paolo Bagnaia - CTF - 3 - Termodinamica
mono-
bi-
poli-
cv
3R/2
5R/2
6R/2
cp
5R/2
7R/2
8R/2
γ=
cp / cv
5/3
7/5
8/6
♠
29
trasformazioni adiabatiche (Q = 0)
• Legge delle adiabatiche :
[ NB facile, ma non dimostrare ]
T1V1γ-1 = T2V2γ-1;
p1V1γ = p2V2γ;
p
I
F
mat. : γ > 1 → adiabatica più “ripida” che isoterma;
fisica : Q = 0 → ∆U = - L →
∆V > 0 → L > 0
→ ∆U < 0 → ∆T < 0.
Paolo Bagnaia - CTF - 3 - Termodinamica
T1
T2
V
♠
30
legge delle adiabatiche
dimostrazione [per curiosità] :
• 1º princ. → dU = ncvdT = dQ - p dV = - p dV ;
• eq. gas → pdV + Vdp = nRdT = n(cp-cv)dT = ncvdT (γ-1);
• - p dV (γ - 1) = p dV + V dp → V dp = - γ p dV;
• dp / p = - γ dV / V ;
p
• ln (pf / pi) = - γ ln (Vf / Vi) =
γ
= ln [ (Vi / Vf) ] ;
γ
• pf Vf =
γ
pi Vi
[QED].
I
F
T1
T2
V
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
31
2º principio della termodinamica (1)
[elenco di fatti sperimentali che sono permessi dal 1º principio,
ma non avvengono nel mondo reale ...]
! [Kelvin] non esiste una trasformazione, il cui unico
risultato sia trasformare integralmente calore in lavoro
da una sorgente ad un’unica temperatura;
! [Clausius] non esiste una trasformazione, il cui unico
risultato sia trasferire calore da un corpo più freddo ad
uno più caldo.
no !!!
Q
L
T
T1
T2
T1<T2
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
32
2º principio della termodinamica (2)
! due enunciati non indipendenti, ciascuno dimostrabile a partire
dall’altro [facile, ma un po’ artificioso, non lo facciamo ...] ;
! principio basato sul concetto di “unico risultato”;
! quindi, occorre definire trasformazioni, in cui lo stato iniziale
coincida con quello finale ( cicli ), e discutere Q e L in queste
trasformazioni;
! definizione di “rendimento termodinamico di un ciclo” η :
η ≡ | L | / | Qassorbito | = ( | Qassorbito | - | Qceduto | ) / | Qassorbito | ;
NB : • | x | significa “valore assoluto” di x;
• per il 1° principio, in un ciclo ∆U = 0 → L = | Qassorbito | - | Qceduto | .
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
33
il ciclo di Carnot : definizione
1. a-b : isoterma a T = T1;
Trasformazione ciclica composta 2. b-c
: adiabatica T : T1 → T2;
da 4 trasformazioni elementari
3. c-d : isoterma a T = T2;
reversibili di un gas perfetto :
4. d-a : adiabatica T : T2 → T1;
p
LTOT =
♦
a
a-b b-c c-d d-a
b
d
Paolo Bagnaia - CTF - 3 - Termodinamica
c
T1
T2
V
TOT
Q
+
0
-
0
+
L
+
+
-
-
+
∆U
0
-
0
+
0
♠
34
il ciclo di Carnot : rendimento
# Qab = Lab = nRT1 ln(Vb / Va ) ;
# Qcd = Lcd = -nRT2 ln(Vc / Vd ) ;
[NB : ln (a/b) = - ln (b/a) ]
# Qab / Qcd  = T1 / T2 [ ln(Vb / Va ) / ln(Vc / Vd ) ];
# T1Vbγ-1 = T2Vcγ-1 ;
# T1Vaγ-1 = T2Vdγ-1 ;
# (Vb / Va)γ-1 = (Vc / Vd)γ-1;
p
a
# Vb / Va = Vc / Vd ;
b
# Qab / Qcd  = T1 / T2 ;
Qab - Qcd ) / Qab =
# η = (
= 1 - T2 / T1.
Paolo Bagnaia - CTF - 3 - Termodinamica
d
c
T1
T2
V
♠
35
ciclo di Carnot : conclusioni
• il ciclo di Carnot è reversibile : pertanto, possiamo
pensare di percorrerlo in senso inverso (“frigorifero”);
• teorema di Carnot :
“nessuna macchina termica
operante tra le temperature
T1 e T2 (< T1) può avere
rendimento superiore al ciclo
di Carnot” :
ηx ≤ ηcarnot = 1 - T2 / T1 ;
Paolo Bagnaia - CTF - 3 - Termodinamica
p
a
b
d
c
T1
T2
V
♠
36
entropia S : trasf. reversibili
• definizione (provvisoria) :
F
in una trasformazione reversibile ∆S = ∫I dQ / T ;
• nel ciclo di Carnot : isoterme ∆S = Q / T ;
adiabatiche ∆S = 0;
in totale : ∆STOT = Q1/T1 + 0 + Q2/T2 = 0; [*]
• una qualsiasi trasformazione ciclica reversibile può
essere approssimata da una somma di cicli di Carnot;
• pertanto ∆S = 0 in ogni ciclo reversibile.
• pertanto S è una funzione di stato.
[*] : Q1 / Q2 = T1 / T2 → Q1 / T1 = - Q2 / T2 .
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
37
cicli reversibili e ciclo di Carnot
p
Si può sempre approssimare un ciclo
reversibile (—) con una “spezzata” di
isoterme (—) e di adiabatiche (—), che
approssimano il ciclo con la precisione
desiderata.
isoterme
V
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
38
entropia S : trasf. irreversibili
• in una trasf. irreversibile, ∆S = ∫I dQ / T non è
F
definita !!!
• soluzione : S è una funzione di stato ;
→ per calcolare ∆S in una trasf. irreversibile, si sceglie
una trasf. reversibile con gli stessi stati iniziale e finale,
si calcola ∆SREV e si definisce ∆SIRREV = ∆SREV ;
p
IRREV. (non disegnabile)
F
REV1; ∆S1 = ∆S2 = ∆SIRREV
REV2
I
V
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
39
entropia : espansione libera
• espansione libera V → 2V :
Q = 0, L = 0 → ∆U = 0 → T = cost.
∆S = ∫ dQ / T = 1/T × ∫ dQ = Q / T = 0
V, gas
no !!!
V, vuoto
• calcoliamo lungo l’isoterma reversibile (∆U = 0) :
∆S = ∫ dQ / T = 1/T ∫ dQ = 1/T ∫ dL =
= ( 1/T ) nRT ln ( VF / VI ) = nR ln ( VF / VI ) = nR ln 2 .
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
40
entropia : riscaldamento irreversibile
# due corpi, entrambi di massa m e calore specifico c, posti a
contatto, raggiungono l’equilibrio termico con una trasformazione
non reversibile;
# calcoliamo le due variazioni di entropia utilizzando due
trasformazioni reversibili, e.g ottenute ponendo entrambi i corpi a
contatto con termostati, e poi diminuendo lentamente la
temperatura del termostato;
# ∆S1 = ∫ dQ / T = mc ∫ dT / T = mc ln (TF / TI) = mc ln [ T / (T+∆T ) ];
# ∆S2 = ∫ dQ / T = ...
...
= mc ln [ T / (T-∆T ) ];
# ∆STOT = ∆S1 + ∆S2 = mc ln [ T 2 / ( T 2 - ∆T 2 ) ];
NB ∆STOT > 0.
Paolo Bagnaia - CTF - 3 - Termodinamica
T+∆T
Q→
T-∆T
♠
41
entropia di un gas perfetto
• consideriamo una qualsiasi trasformazione di un gas perfetto, tra
uno stato I [pI VI TI] e uno stato F [pF VF TF] ;
• calcoliamo ∆S lungo una qualsiasi trasf. reversibile tra I e F :
# dU = dQ - dL → dQ = dU + dL ;
[ tr. reversibile ]
# dQ = n cv dT + p dV = n cv dT + n R T dV / V ;
[ gas perfetto ]
# dQ / T = n cv dT / T + n R dV / V ;
# ∆S = ∫ dQ / T = n cv ln ( TF / TI ) + n R ln ( VF / VI ) ;
= n (cv + R ) ln ( VF / VI ) + n cv ln ( pF / pI ) ;
# ∆S = n cp ln ( VF / VI ) + n cv ln ( pF / pI ) ;
[TV]
[TF / TI = pFVF / pIVI]
[pV]
= n cp ln ( TF / TI ) + n ( cv - cp) ln ( pF / pI ) ;
# ∆S = n cp ln ( TF / TI ) - n R ln ( pF / pI ) ;
Paolo Bagnaia - CTF - 3 - Termodinamica
[pT]
♠
42
entropia : conclusioni
a)
b)
l’entropia è una funzione di stato → non dipende dalla
trasformazione, ma solo dagli stati iniziali e finali → il calcolo è
valido per qualsiasi trasformazione;
alternativamente, si può usare il calcolo precedente per
dimostrare che, poichè ∆S dipende solo dagli stati iniziale e
finale → S è una funzione di stato.
p
F
dU = dQ - dL
I
V
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
43
Fine parte 3
Paolo Bagnaia - CTF - 3 - Termodinamica
♠
44
Elettromagnetismo
! elettrostatica
"
"
"
"
"
"
legge di Coulomb;
campo elettrico;
teorema di Gauss;
potenziale elettrostatico;
capacità e condensatori;
campi elettrici nella materia;
! correnti continue
" legge di Ampère;
" solenoide;
" toroide;
! induzione
elettromagnetica
" legge di FaradayNeumann-Lenz;
" induttanza;
" circuito RL;
" leggi di Ohm;
" forza elettro-motrice;
" resistenze e circuito RC;
! equazioni di Maxwell
" legge di Biot-Savart;
[vedi → onde elettromagnetiche]
! campi magnetici
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠
1
La legge di Coulomb nel vuoto
1 q 1q 2
F =
2
4 π ε 0 r12
→
r12
!""#""$
q1
Paolo Bagnaia - CTF - 4a - Elettrostatica
q2
ε0 = 8.85 × 10-12 C2 / [N m2] ;
1/(4πε0) = 8.99 × 109 N m2 / C2
+
+
-
-
+
♠
2
la legge di Coulomb : commenti
• nuova unità MKS : coulomb [ C ] (molto grande) ;
• q1 e q2 nel vuoto; ε0 = “costante dielettrica del vuoto” ;
• analoga alla legge di gravitazione, tranne segno “ ±q ” ;
• la carica elettrica si conserva (cfr. massa) ;
• la carica elettrica è discreta : q = ± N e [N molto grande] ;
• qprotone = 1.6 × 10-19 C = -qelettrone = -e ;
• natura simmetrica se q↔-q (tutte le cariche cambiano segno);
• qelettrone < 0 → scelta (a posteriori, non troppo felice).
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠
3
campi vettoriali
definire :
"
"
"
"
"
sorgenti e pozzi;
linee di campo;
superfici equipotenziali;
flusso;
integrale di linea;
+
-
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠
4
linee di campo
+
-
ex. campo di dipolo
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠
5
Il campo elettrico
• concetto di campo vettoriale : v = v (x,y,z) ;
+
• linee di campo escono da +q, entrano in -q ;
• E = F / q0 [ “carica esploratrice” ] ;
2
• q puntiforme → E = q / ( 4πε0 r ) ;
• q distribuzione qualsiasi, E(x,y,z) contiene l’informazione
completa [è equivalente conoscere la distribuzione delle cariche,
oppure il campo elettrico in tutto lo spazio] ;
• il campo è additivo : ETOT = E1 + E2 + E3 + ...
• forza su carica q in (x,y,z) : F = E(x,y,z) × q ;
• E si misura in N / C (oppure -vedi oltre - in V / m).
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠
6
Campo elettrico di dipòlo
• applicazioni importanti (ex. molecola d’acqua H2O) ;
• caso particolare : lungo l’asse del dipolo :
E TOT = E + + E −

q
q
1 
=
−

 =
2
2
4 π ε 0  (z − d / 2 )
(z + d / 2 ) 

q 
1
1
=
− 2
=


2
2
2
4 π ε 0  z − dz + d / 4 z + dz + d / 4 
=
q
z+d −z+d
qd
p
2 qd
=
=
=
4π ε 0 z
z2 − d 2
4π ε 0 z 3
2π ε 0 z 3
4π ε 0 z 3
-
d
Paolo Bagnaia - CTF - 4a - Elettrostatica
+
z
P
♠
7
Flusso del campo elettrico
• Definizione di flusso di un campo vettoriale v
attraverso una superficie S, di cui n è il vettore unitario
normale (versore) :
Φv(S) = v · n S
[oppure]
Φv(S) = ∫ v · n dS
• caso particolare :
v è il campo elettrico E .
S
^
n
→
v
NB :
" S è una superficie geometrica “ideale”;
" Φv(S) è uno scalare, che dipende da vettori.
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠
8
Teorema di Gauss
Data una superficie chiusa S ed un campo
elettrostatico E :
ΦE(S) =
∫ E·n
dS = Σi qi / εo ;
la somma algebrica Σi è estesa a tutte le cariche
contenute nella superficie S.
NB • il teorema di Gauss è matematicamente equivalente alla
legge di Coulomb;
• è un potente strumento di calcolo dei campi elettrici (cfr.
conservazione dell’energia in meccanica).
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠
9
campi elettrici : carica puntiforme
• carica puntiforme Q :
E(r) = 1/(4πε0) Q / r 2 ;
S
Φ (E) = Σ ds E · n =
= 4πr 2×1/(4πε0) Q/r 2
= Q / ε0
Φ (E)= Σ ds E · n =
= 4πr 2× E = Q / ε0;
⇒ E(r) = 1/(4πε0) Q / r 2.
Paolo Bagnaia - CTF - 4a - Elettrostatica
Q
E
QED
♠ 10
campi elettrici : guscio sferico
conseguenze :
!un guscio sferico produce
all’esterno lo stesso campo di
una carica puntiforme;
!all’interno di un guscio sferico
carico in modo uniforme il
campo è nullo.
S
Q
E
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 11
campi elettrici : sfera piena
sfera piena
(raggio R, carica Q) :
r
a) esterno (r>R) :
E(r) = 1/(4πε0) Q / r 2 ;
R
b) interno (r<R) :
E
2
Φ (E)= 4πr ×E = q/ε0 =
= Q/ε0 (4/3 π r 3) / (4/3 π R 3);
∼r
E = Q / (4π ε0) r / R 3.
∼1/r2
R
Paolo Bagnaia - CTF - 4a - Elettrostatica
r
♠ 12
campi elettrici : filo carico
• filo carico, densità λ = dQ/dx :
Φ (E)= Φ (E, mantello) + Φ (E, tappi) =
[Φ (E, tappi) = 0 ]
=SE=
= 2πrh × E = λ × h / ε0 ;
E = 1/(2πε0) λ /r .
E
r
[NB : E ∼ 1/r ]
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 13
campi elettrici : strato
• strato carico piano, densità σ = dQ/dS :
Φ (E) = Φ (E, mantello) + Φ (E, tappi) =
[Φ (E, mantello) = 0 ]
= 2S E = Q / ε0 = σ S / ε0 ;
E = σ / 2 ε0.
S
E
NB E non dipende dalla distanza punto-piano
carico !!! capire bene le approssimazioni implicite ...
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 14
campi elettrici : doppio strato
• doppio strato carico (due piani
indefiniti paralleli, con densità ±σ) ;
• tre zone dello spazio : a,b,c
(somme vettoriali);
a) E = 0;
b) E = E+ + E- = σ / ε0 ;
c) E = 0.
Paolo Bagnaia - CTF - 4a - Elettrostatica
S
+ -
0
a)
0
b)
c)
♠ 15
conduttori ed isolanti
• si chiamano “isolanti” quei corpi (ex. legno, vetro, ceramica) in cui
le cariche elettriche NON possono muoversi; l’elettrostatica degli
isolanti è simile a quella del vuoto (vedi oltre ε0 → ε0 εr);
• si chiamano “conduttori” (ex. metalli) quei corpi, all’interno dei
quali le cariche elettriche scorrono liberamente (meglio, gli
elettroni degli orbitali esterni sono liberi); l’elettrostatica dei
conduttori richiede che le cariche elettriche siano in equilibrio
elettrostatico tra loro (cfr. l’acqua in un sistema di condotti).
+
-
+
+
Paolo Bagnaia - CTF - 4a - Elettrostatica
isolante
+
+
-
-
+
+
conduttore
+
-
♠ 16
campo elettrico di un conduttore
• situazione statica (= cariche ferme);
• campo interno E = 0 (se E ≠ 0, le
cariche si muovono);
• teorema di Gauss per la superficie “…”
→ carica nulla all’interno del corpo
→ tutte le cariche (Q) si dispongono
sulla superficie;
• il campo E sulla superficie del corpo è
ortogonale alla superficie stessa (la
componente parallela metterebbe le
cariche in movimento).
Paolo Bagnaia - CTF - 4a - Elettrostatica
E
E=0
Q
♠ 17
potenziale elettrico
• la forza elettrostatica è conservativa (cfr. forza
gravitazionale);
• pertanto, esiste l’energia potenziale e.s. :
B
∆UAB = UB - UA = -LAB = - ∫A F · dx ;
• si definisce il “potenziale e.s.” V ;
• ∆VAB è il lavoro della forza e.s. per portare una carica q0
dal punto A al punto B, diviso q0 :
∆VAB = VB - VA = ∆UAB / q0 = -LAB / q0
B
A
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 18
potenziale elettrico (2)
• ∆VAB non dipende dal cammino della carica, ma solo dai
punti iniziale e finale;
• ∆VAB è l’integrale del campo elettrico tra A e B :
∆VAB = - LAB / q0 = - ∫
B
A
F · dx / q0 = - ∫
B
A
E · dx ;
• nel caso di carica puntiforme q :
B
∆VAB, puntiforme = - ∫A E · dx = q/(4πε0) [ 1/rB - 1/rA ] ;
• usualmente si sceglie la “costante” di V in modo che il
valore di V(∞) sia zero :
∆V∞X = VX - V∞ = VX
Paolo Bagnaia - CTF - 4a - Elettrostatica
B
A
♠ 19
il volt
• unità di misura MKS del potenziale elettrico :
1 Volt = 1 V = 1 Joule / 1 Coulomb
• utilizzando il Volt, il campo elettrico può essere
misurato in :
[campo] = [forza / carica] = N / C =
= N × m / ( C × m ) = Volt / m
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 20
superficie equipotenziale
• “superficie equipotenziale” : luogo dei
punti con lo stesso potenziale [dati due
punti A e B su una s.e., ∆VAB=0];
• se il campo è generato da una carica
puntiforme, le s.e. sono sfere centrate
nella carica;
•
s.e.
E
E in un punto è
ortogonale alla s.e. passante nel punto.
[si potrebbe dimostrare che]
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 21
capacità
• si definisce “capacità elettrica” di un conduttore (C) il
rapporto tra la carica portata sul conduttore e il
corrispondente aumento di potenziale :
C = Q / ∆V
• C si misura in Farad (F) : 1 Farad = 1 F = C / V ;
• per un conduttore isolato, ∆V ∼ Q → C non dipende da
Q e da ∆V → dipende solamente dalla geometria dei
conduttori;
• si chiama “induzione completa” il caso in cui tutte le linee di campo che escono
da un conduttore entrano in un secondo (ex. il doppio strato);
• un sistema di conduttori in situazione di i.c. costituisce
un “condensatore”.
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 22
condensatori
• un condensatore è costituito da due
“armature” (ex. piatti), una delle quali è
caricata +Q (ex. con una pila, vedi oltre);
• l’altra armatura, in condizioni di induzione
completa, acquista una carica -Q ;
• la carica totale del condensatore è QTOT =
= +Q -Q = 0;
• in elettrotecnica, un condensatore si
disegna come due sbarrette affacciate
(vedi a lato);
• in commercio si trovano c. da 10-6÷10-12 F.
Paolo Bagnaia - CTF - 4a - Elettrostatica
+ -
-
+
-
+
♠ 23
condensatore piano
•
•
•
•
campo tra le armature (doppio strato) E = σ / ε0 ;
d.d.p. ∆V = ∫ E·dx = E d ;
carica Q = σ × S ;
capacità C = Q / ∆V = σ S / (E d) = σ S ε0 / (σ d)
= ε0 S / d.
+ -
d
S
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 24
condensatore cilindrico
• altezza del cilindro : h ;
• campo tra le armature (filo carico) :
E = [ 1/(2πε0) λ/r = ] q / (2πε0 rh ) ;
• d.d.p. ∆V = ∫ E·dr = q / (2πε0h) ln (b/a) ;
• carica Q = q ;
• capacità C = Q / ∆V
C = q (2πε0h) / [q ln (b/a) ] =
= 2πε0h / ln (b/a) .
Paolo Bagnaia - CTF - 4a - Elettrostatica
b
a
♠ 25
condensatore sferico
• campo tra le armature (guscio sferico) :
E = q / (4πε0 r2 ) ;
• d.d.p. ∆V = ∫ E·dr = q / (4πε0) [1/a - 1/b] ;
• carica Q = q ;
• capacità C = Q / ∆V = (4πε0) / [1/a - 1/b]
= 4πε0 ab / (b - a) .
b
a
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 26
condensatori in serie / parallelo
!serie : ∆VTOT= ∆V1 + ∆V2 ; q1+ = q1- = q2+ = q2- ≡ q;
" ∆VTOT = q/C1 + q/C2 = q (1/C1 + 1/C2 );
" 1/CTOT = 1/C1 + 1/C2.
!parallelo: ∆V1 = ∆V2 ≡ ∆V ; q1 = C1∆V ; q2 = C2∆V;
" q = q1 + q2 = C1 ∆V + C2 ∆V = (C1 + C2 )∆V ;
" CTOT = C1 + C2.
C1 C2
Paolo Bagnaia - CTF - 4a - Elettrostatica
C1
C2
♠ 27
campi elettrostatici nella materia
" spiegazione microscopica : se un isolante si trova in un
campo elettrico, le sue molecole si deformano (→ piccoli
dipoli) [oppure le molecole sono piccoli dipoli anche in
assenza di campo elettrico, ex. acqua];
" i dipoli di allineano al campo elettrico, e in questo modo
complicano la distribuzione di cariche;
" → il campo totale è la risultante di tutti questi effetti;
" regola empirica : ogni materiale possiede una “costante
dielettrica” εr, un numero puro > 1; le leggi dell’elettrostatica si modificano nella materia : ε0 → ε0 εr ;
" ex. legge di Coulomb : F = 1/(4πε0 εr) Q/r2 ;
"
capacità di un condensatore piano : C = ε0 εr S / d.
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 28
Fine parte 4a
Paolo Bagnaia - CTF - 4a - Elettrostatica
♠ 29
la corrente elettrica
+ +
+
-
-
+ +
+
-
+
-
+
+
-
-
+
- -
+
-
+ +
- - -
• le cariche sono libere di muoversi all’interno dei
conduttori;
• una superficie ortogonale all’asse di un
conduttore è attraversata da una carica q
nell’unità di tempo :
i = dq / dt
! unità di misura : 1 Ampère = A = C / s.
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠
1
densità di corrente
• il conduttore ha superficie S, normale al suo asse;
• si chiama “densità di corrente” J (vettore parallelo alla
velocità delle cariche positive)[*] :
J= J = i / S = 1/S dq/dt
• detto n il numero di elettroni di conduzione per unità di
volume, v la velocità media degli elettroni, e la loro
carica [*] :
L
S
q = Nel e = n V e = (n S v ∆t ) e ;
i = dq /dt = n S v e ;
- -- - - - - J=nve.
-- [*] NB attenzione al verso, l’elettrone ha carica negativa !!!
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠
2
leggi di Ohm
• per molti conduttori (conduttori “ohmici”, ex. metalli) :
V / i = costante = R
• Ri=RJS=V=EL→E=RJS/L≡ρJ
L
S
R=ρL/S
• R in Volt / Ampere = Ohm = Ω ;
• ρ (resistività) dipende dal tipo di materiale e dalle sue
condizioni (ex. temperatura);
• ρ in Ω m; per i metalli ρ = (1 ÷ 50)×10-8 Ω cm.
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠
3
elettroni nei metalli
! modello a “elettroni liberi”, di massa m e carica e :
"
"
"
"
senza campo elettrico, gli elettroni si muovono liberamente nel conduttore;
collidono con gli atomi del reticolo cristallino, in media dopo un tempo τ;
la velocità quadratica media dipende da : temperatura + effetti quantistici;
la velocità media vettoriale è nulla (vq.m.∼106 m/s, vM = 0);
! un campo elettrico E modifica la situazione :
" la velocità media vettoriale è data da F = ma = eE → vM = aτ = eEτ / m ;
[NB vM ∼10-5 m/s] ;
" poiché vM = J / ne → E = vMm / eτ = Jm / ne2 τ
" poiché E = ρJ → ρ = m / ne2 τ ;
! affinché la legge di Ohm sia valida, ρ deve essere costante e non
dipendere da E → τ non dipende da E (vero se vM << vq.m.).
-
-
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
+
-
-
+
-
+
♠
4
energia nei circuiti elettrici
•
•
•
•
campo E : accelerazione costante degli elettroni;
legge di Ohm : corrente costante ( → velettroni costante);
la resistenza dissipa energia (potenza dissipata);
calcoliamo gli effetti energetici della corrente :
" dU = V dq = V i dt ;
" potenza W = dU / dt = V i ;
R
" W = V i = i 2 R = V 2 / R.
V
[se R aumenta, W aumenta ? diminuisce ? ]
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
-
+
♠
5
forza elettro-motrice
• f.e.m. di un generatore : ƒ = dL / dq ;
• differenza di potenziale (d.d.p.) ↔ (f.e.m.) ;
• dL = ƒ dq = ƒ i dt = i 2 R dt → ƒ = i R [simile alla l. di.Ohm] ;
• definizione di “resistenza interna” di un generatore;
• NB : la forza associata alla f.e.m. NON è conservativa.
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠
6
circuiti elettrici
elementi dei circuiti :
" generatore di f.e.m.
∆V = ƒ
" resistenza
∆V = R i
R
" condensatore
∆V = Q / C
C
" induttanza
∆V = L di/dt
L
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
-
+
∆V
♠
7
leggi dei circuiti
• definizione di
+
“generatore”;
“resistenza interna”;
“circuito”;
“nodo”;
“maglia”.
-
!
!
!
!
!
-
+
• leggi dei circuiti :
! la somma algebrica delle d.d.p. in una maglia è nulla;
! la somma algebrica delle correnti in un nodo è nulla;
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠
8
resistenze in serie e in parallelo
"serie : i1 = i2 ≡ i ; ∆VTOT = ∆V1 + ∆V2 ;
! ∆VTOT = i R1 + i R2 = i (R1 + R2 );
! RTOT = R1 + R2.
"parallelo: ∆V1 = ∆V2 ≡ ∆V ;
! i = i1 + i2 = ∆V / R1 + ∆V / R2 = ∆V (1/R1 + 1/R2 ) ;
! 1 / RTOT = 1 / R1 + 1 / R2.
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
[ → RTOT = R1 R2 / (R1 + R2)]
♠
9
circuito RC : carica
! legge dei circuiti : ƒ - i R - q / C = 0;
! ƒ=iR+q/C;
q(t=0) = 0;
! ƒ = R dq / dt + q / C ;
[equazione differenziale]
R
! q(t) = qC(t) = Cƒ [1 - e - t / (RC) ] ;
! i(t) = dq / dt = ƒ e - t / (RC) / R ;
! ∆VC(t) = qC(t) / C = ƒ [1 - e - t / (RC) ] ;
C
ƒ
+
-
! ∆VR(t) = R i(t) = ƒ e - t / (RC) ;
NB : ∆VC(t) + ∆VR(t) = ƒ
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
[QED]
♠ 10
circuito RC : carica (2)
∆V
ƒ
∆VC = qC(t) / C
R
∆VR = R i(t)
0
C
ƒ
t
+
-
! ∆VC(t) = qC(t) / C = ƒ [1 - e - t / (RC) ] ;
! ∆VR(t) = R i(t) = ƒ e - t / (RC) ;
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 11
circuito RC : scarica
! non c’è più il generatore ƒ ; q(t=0) = q0 ;
! R dq / dt + q / C = 0;
[equazione differenziale]
! q(t) = qC(t) = q0 e - t / (RC) = V0 C e - t / (RC) ;
! i(t) = dq / dt = - V0 e - t / (RC) / R .
[ NB : “-” ]
| i(t) |
V0/R
R
C
i(t)
0
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
t
♠ 12
energia di un condensatore
• dall’eq. precedente [ i(t) = dq / dt = - V0 e - t / (RC) / R ] :
• W = V 2 / R = i 2 R = V02 e - 2t / (RC) / R ;
• L=∫
∞
W dt = V02 / R ∫o e
- 2t / (RC)
dt = ½ C V02 ;
• altro metodo [portiamo una carica dq attraverso la ddp V ] :
• dL = V dq = q dq / C ;
• L=∫
∞
dL = ∫o q(t) / C dq = ½ q02 / C = ½ C V02 .
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 13
campo magnetico B
• fenomeni magnetici in natura (calamita, elettrocalamita,
etc.);
• analogia : il campo elettrico E è definito dalla forza su
una carica q ferma, il campo magnetico B dalla forza su
una carica q in movimento con velocità v :
FE = q E ↔
FM = q v ∧ B
[ forza di Lorentz ]
• B si misura in “Tesla” (T) : T = N / (C m / s ) = N / (A m)
[in CGS anche Gauss (G) : 1 Gauss = 10-4 T] .
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 14
campo B : esempi
campo B costante lungo z : B = B k ;
! v1 lungo z : v1 = v1 k :
z
! B ∧ v1 = 0 → FM = 0;
! traiettoria rettilinea.
v1
! v2 lungo y : v2 = v2 j :
! FM = q v2 B ;
! forza costante in modulo, sempre
ortogonale a v2 ;
! traiettoria : moto circolare uniforme;
! q v2 B = m v22 / r → r = m v2 / ( q B ).
B
x
y
v2
! v qualsiasi : traiettoria ad elica .
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 15
proprietà del campo magnetico
• esperienza della “calamita spezzata”;
• in natura, non esistono “monopoli magnetici”, l’analogo
delle cariche elettriche per il campo magnetico;
• dal punto di vista dei campi vettoriali, il campo
magnetico non ha “sorgenti” né “pozzi”, le sue linee di
campo sono tutte linee chiuse.
N
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
S
N
S
N
S
♠ 16
forza su un filo percorso da corrente
[per semplicità, i ⊥ B]
• su un elettrone nel filo {m, e, v} :
F=evB;
• su un tratto del filo { lunghezza L, sezione S,
elettroni/Volume n } :
FTOT = Nel. e v B = n L S e v B = i L B ;
xB
i
• definito un vettore L parallelo al filo, nel
caso generale [angolo filo/campo qualsiasi] :
FTOT = i L ∧ B.
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 17
legge di Biot-Savart
un filo rettilineo indefinito, percorso da una
corrente i genera in tutto lo spazio un campo
magnetico B, che in un punto P distante r dal
filo vale :
! il modulo |B| :
B = µ0 i / (2πr);
µ0=1.26×10-6 T m / A;
! la direzione di B è tangente alla
circonferenza, passante per il punto P,
giacente sul piano ortogonale al filo e
centrata nel filo;
r
P
B
i
! il verso di B segue la “regola della mano
destra” (pollice || i, indice || B);
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 18
correnti → campi magnetici
analogia E ↔ B :
• una carica elementare dq genera un campo elettrico :
dE = 1 / (4πε0) dq r / r 3 ;
• un pezzetto elementare di filo ds percorso da corrente i
genera un campo magnetico :
dB = µ0 / (4π) i ds ∧ r / r 3.
i
dB
×
dq
r
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
dE
ds
r
♠ 19
spira percorsa da corrente
spira di raggio percorsa da corrente i :
! dB = µ0 / (4π) i ds ∧ r / r 3;
! s⊥r;
! B = µ0 i / (4π) ∫ ds / r 2 = µ0 i / (4π) 2πr / r 2 =
= µ0 i / (2r).
B
i
r
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 20
due conduttori paralleli
! la corrente i1 genera un campo magnetico che esercita
una forza sul filo 2 [ F12 ] ;
! la corrente i2 genera un campo magnetico che esercita
una forza sul filo 1 [ F21 ] ;
! F12 = i2 L B1 = µ0 L i1 i2 / (2πd) = i1 L B2 = F21 ;
! correnti concordi → forze attrattive;
! correnti discordi → forze repulsive.
NB questo metodo è quello realmente usato per misurare
con precisione le correnti (→ definizione dell’ Ampère)
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
i1
i2
d
♠ 21
la legge di Ampère
il valore di ∫ B · ds (prodotto scalare tra il campo
magnetico e l’elemento di linea), calcolato per una
linea chiusa è uguale alla somma algebrica delle
correnti concatenate con la linea chiusa, moltiplicato
per µ0 :
→
∫ B ⋅ ds = µ o
→
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
∑ (± i )
concatenat e
B
ds
x
i1
•
i2
♠ 22
la legge di Ampère : commenti
" c’è parallelismo tra elettrostatica e magnetismo :
↔ legge di Coulomb
↔ legge di Gauss ;
carica
corrente ↔ legge di Biot-Savart ↔ legge di Ampère.
→
∫ B ⋅ ds = µ o
→
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
∑ (± i )
concatenat e
B
ds
x
i1
•
i2
♠ 23
la legge di Ampère : filo indefinito
• [si ritrova il valore della legge di Biot-Savart]
•
∫ B · ds = 2π r B = µ0 i →
→ B = µ0 i / (2π r ).
ds
B
∑ (± i )
∫ B ⋅ ds = µ o concatenat
e
→
→
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
•
i
r
♠ 24
la legge di Ampère : solenoide
• ∫ B · ds =
= ∫a,int B · ds + ∫b B · ds + ∫a,ext B · ds + ∫b B · ds =
= ∫a,int B · ds = B a = µ0 iTOT = µ0 i N = µ0 i n a →
→ B = µ0 i n.
b
a
B
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 25
la legge di Ampère : toroide
• ∫ B · ds = B 2π r = µ0 iTOT = µ0 i N
→
→ B = µ0 i N / (2π r ).
r
B
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 26
legge di Faraday-Neumann-Lenz
• Φ (B) =∫ B ·dA = ∫ B ·n dA;
• 1 Weber = 1 Tesla × 1 m2;
• Φ (B) non dipende dalla scelta della
superficie A, è lo stesso per tutte le
superfici delimitate dalla stessa linea;
• legge di F.-N.-L. : quando il flusso
concatenato con una spira varia nel
tempo, si induce nella spira una f.e.m.
S
N
ƒ = - d Φ (B) / d t.
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 27
legge di Lenz
• se la spira è conduttrice, con
resistenza R, si genera una corrente :
i = - 1/R dΦ (B) / d t;
• la corrente i, a sua volta, genera un
campo magnetico, il cui flusso si
oppone alla variazione di flusso che lo
ha generato (significato del “-”) :
B → Φ (B) → dΦ (B) / dt → ƒ → i →
B’ → Φ (B’) opposto a Φ (B).
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
B
(aumenta)
i
B’
♠ 28
correnti indotte
• B ⊥ A ; A costante ; B varia :
ƒ = - dΦ/dt = - d(BA) / dt = -A dB/dt;
i = A/R dB/dt.
• B ⊥ A ; B costante ; A varia (ex. si stringe) :
ƒ = - dΦ/dt = - d(BA) / dt = -B d(bh)/dt = Bhv;
i = Bhv / R; F = ihB = B2h2v / R; W = B2h2v2 / R.
h
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
•
B
v
♠ 29
correnti alternate
• in una spira rotante in un campo
magnetico costante si induce una
corrente “alternata”, di periodo pari
a quello della rotazione della spira;
• B = costante; A = costante;
θ = angolo(B,A) = ωt ;
ƒ = - dΦ /dt = -BA d(cosθ) / dt
= BA ω sin(ωt);
i = BA ω sin(ωt) / R.
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
B
♠ 30
induttanza
• [simile alla capacità in corrente continua];
• dato un circuito elettrico di N spire, attraversato da una
corrente i, che induce un campo magnetico B, il cui
flusso concatenato è Φ(B), si definisce “induttanza” del
circuito il valore
L ≡ N Φ (B) / i
• ex. solenoide di lunghezza d, area A, N spire :
B = µ0in → NΦ (B) = ( n d )( B A ) = µ0 i n2 d A →
[N.B. L non è funzione della corrente i ].
L = µ0 n2 d A
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 31
autoinduzione
• in una bobina di induttanza L passa una corrente
i, variabile nel tempo :
ƒ = - dΦ /dt = - d [ iL ]/dt = - L d i /dt
• L si misura in henry :
1 henry = 1H = 1 T · 1 m2 / 1 A.
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 32
circuito RL (cenni)
• -iR - Ldi/dt + ƒ = 0;
• ƒ = iR + Ldi/dt ;
• i = ƒ / R [1 - e-tR/L ];
R
∆V
L
ƒ
ƒ
+
∆VR = R i
-
∆VL = -Ldi/dt
0
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
t
♠ 33
equazioni di Maxwell (cenni)
tutto l’elettromagnetismo in quattro equazioni :
A. legge di Gauss del campo elettrico (→ legge di Coulomb) :
∫S E · dA = q / ε0 ;
B. legge di Gauss del campo magnetico (→ calamita spezzata) :
∫S B · dA = 0;
C. legge dell’induzione di Faraday :
∫L E · ds = -d Φ (B) /d t ;
D. legge di Ampère (+ correzione di Maxwell) :
∫L B · ds = µ0 ε0 d Φ (E) /d t + µ0 i.
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 34
Fine parte 4b
Paolo Bagnaia - CTF - 4b - Elettromagnetismo
♠ 35
Onde e ottica
!Onde
!Ottica
" proprietà delle onde;
" la luce;
" onde sonore;
" il principio di Huygens;
" il decibel;
" la rifrazione;
" ottica geometrica;
" riflessione e rifrazione;
" specchi, lenti, microscopi.
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
1
le onde
•
•
•
•
y
onde del mare, corde vibranti, onde elettromagnetiche ...
fenomeno periodico (T);
caso semplice : onda sinusoidale in due dimensioni;
l’onda si muove nello spazio e nel tempo.
t=0
t=T/2
t=T/4
x
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
2
parametri delle onde
• y(x,t) = A sin (kx -ωt ) =
= A sin (2πx/λ - 2πt/T );
• ampiezza A ;
• periodo T = 2π / ω ;
• lunghezza d’onda λ = 2π / k.
y
λ
y
A
t=0
x=0
A
x
t
T
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
3
velocità delle onde
• [attenzione al significato di “velocità”] ;
• in un tempo T [= periodo] una cresta si sposta di una
distanza λ [= lunghezza d’onda];
• più in generale, v si calcola da : kx - ωt = costante;
• v = ∆x / ∆t = λ / T = ω / k = λν ;
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
4
il suono
• le onde sonore sono “longitudinali”;
• il mezzo vibrante è il corpo interposto tra la sorgente
(ex. violino) e il ricevitore (ex. orecchio) : in genere aria;
• il metodo elementare di propagazione sono gli urti tra le
molecole del mezzo;
• il mezzo, in media, non si muove;
• i fronti d’onda sono sfere centrate nella sorgente.
min max min max
vonda
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
S
♠
5
misura del suono : il decibel
• la sorgente emette suoni con potenza WS;
• un ricevitore a distanza r, di superficie S, riceve una
potenza WR = WS × S / (4 π r 2) ;
• si definisce “intensità sonora” I = WR / S = WS / (4 π r 2);
• l’intensità sonora si misura in Watt / m2;
• altro modo di misurare (più usato) :
β = log10(I / I0) [=“bel”];
I0 = 10-12 W / m2 = intensità minima udibile;
intensità in decibel (dB) = 10 × β = 10 log10(I / I0).
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
6
le onde elettromagnetiche
[trattazione qualitativa, si può dimostrare dalle eq. di Maxwell]
•
•
•
•
le onde e.m. sono onde trasversali del campo e.m. ;
la loro velocità nel vuoto è costante [c=3×108 m/s] ;
c = 1 / √ε0µ0 ;
“costante” significa indipendente da :
" proprietà delle onde (frequenza, lunghezza d’onda, ampiezza);
" sistema di riferimento della misura (¿?) → relatività speciale;
• pertanto, per un’onda e.m. nel vuoto :
λν = c,
i.e. lunghezza d’onda e frequenza non sono
indipendenti, λ = c / ν , ν = c / λ.
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
7
proprietà delle onde e.m.
y
E
• x : propagazione dell’onda;
x
• y : campo elettrico E;
• z : campo magnetico B.
z
z
z
y
B
B
x
E
y
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
x
♠
8
la luce
λ (m)
108 ÷ 104
onde lunghe
101 ÷ 104
103 ÷ 10-1
onde radio
105 ÷ 1010
10-3 ÷ 10-6
infrarosso
1011 ÷ 1014
700 ÷ 400nm visibile
4÷7.5×1014
10-7 ÷ 10-9
ultravioletto
1015 ÷ 1017
10-9 ÷ 10-11
raggi X
1017 ÷ 1019
<10-11
raggi γ
> 1021
luce visibile
700 nm
400 nm
ν (Hz)
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
9
principio di Huygens
s
t=0
principio di Huygens
“la luce si propaga con onde sferiche.
Tutti i punti sulla superficie di un fronte
d’onda si comportano come sorgenti
puntiformi di un nuovo fronte d’onda
sferico.
L’onda
totale
è
data
dall’inviluppo delle onde elementari”.
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
t=s/c
♠
10
principio di Huygens - fenditure
! caso (a) : una
fenditura,
onda sferica;
! caso b) : due
fenditure, due
onde sferiche,
interferenza.
a)
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
b)
♠
11
indice di rifrazione
• la velocità v della luce nei mezzi è minore di
quella nel vuoto;
• definiamo l’indice di rifrazione n :
c
n=c/v
• se v ≤ c :
1≤n≤∞
v=c/n
• n dipende da :
" proprietà del mezzo;
" [quasi indipendente dalle] proprietà della luce (λ).
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
12
rifrazione
• note le proprietà dei mezzi
[n1, n2, v1=c/n1, v2=c/n2] e le
proprietà del raggio incidente
[λ1, θ1], trovare le proprietà
del raggio rifratto [λ2, θ2];
• ∆t1 = λ1 / v1 = ∆t2 = λ2 / v2 →
→ λ1 / λ2 = v1 / v2 ;
• triangoli BAC e BDC :
BC = λ1 / sin θ1 = λ2 / sin θ2 →
→ sin θ1 / sin θ2 = λ1 / λ2
= v1 / v2
= n2 / n1
[legge della rifrazione]
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
n1,v1
λ1
A
θ1
B
θ2
C
D
n2,v2
λ2
♠
13
ottica geometrica
• approssimazioni :
" “dimentichiamo” che la luce è un’onda e.m.;
" assumiamo che sia data da “raggi” che si propagano in linea
retta nei mezzi omogenei trasparenti;
" alcuni mezzi sono riflettenti (= specchi) → leggi della
riflessione;
" assumiamo valida la legge della rifrazione (riformulata, vedi
seguito) quando i raggi incontrano una superficie di
separazione tra due mezzi trasparenti;
• ricaviamo, con semplici dimostrazioni geometriche, leggi
valide per specchi, lenti, microscopi, occhio umano,
macchine fotografiche, etc.
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
14
leggi della riflessione
• leggi della riflessione:
1) angolo di incidenza θ = angolo di riflessione;
2) raggio incidente, raggio riflesso e normale coplanari.
[NB se superficie riflettente non planare, si prende la normale nel
punto di incidenza → ex. specchi sferici]
θ
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
θ
♠
15
rifrazione in ottica geometrica
n1,v1
λ1
A
θ1
B
n1,v1
θ1
θ2
C
θ2
D
n2,v2
λ2
n2,v2
ottica ondulatoria (legge di Huygens) → ottica geometrica (legge di Snell)
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
16
leggi della rifrazione
• leggi della rifrazione (SnellCartesio) :
1) legge dei seni :
θ1 = raggio inc. -normale
θ2 = raggio rifr. -normale
sin θ1 / sin θ2 = n2 / n1;
2) raggio inc., raggio rifr.,
normale sono coplanari.
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
n1,v1
θ1
θ2
n2,v2
♠
17
il prisma
• n dipende da λ per tutti i materiali
• ex. quarzo :
" n(λ=400 nm) = 1.52;
" n(λ=500 nm) = 1.51;
" n(λ=700 nm) = 1.50;
• un prisma investito da un raggio
di luce bianca (mistura di più λ)
separa la luce di differenti λ;
→ escono raggi colorati;
luce
a
• ex arcobaleno.
bianc
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
18
riflessione totale
" sin θ1 / sin θ2 = n2 / n1;
→ sin θ2 = n1 / n2 sin θ1 ≤ 1;
n2
→ sin θ1 ≤ n2 / n1 ;
→ θ1 ≤ asin(n2 / n1) ;
• se θ1 > θc = asin(n2 / n1)
→ riflessione totale (ex. fibre
ottiche).
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
n1
n2 < n1
♠
19
specchi piani
•
•
•
•
•
riflessione;
def. di oggetto e immagine;
immagine reale o virtuale;
immagine diritta o capovolta;
per gli specchi piani :
o
i
" |p| = |i| ;
" i=-p;
" immagine virtuale, diritta.
[per convenzione, p>0, i>0 se reale,
i<0 se virtuale]
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
20
specchi sferici : elementi
definizioni :
• specchio concavo (ex, altri casi
possibili);
• PC = r = raggio dello specchio;
• OC = asse dello specchio;
• F = fuoco = punto in cui
convergono tutti i raggi paralleli
all’asse;
• OF = f = distanza focale;
• dimostreremo :
f = ½ r.
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
S
P
C
O
F
♠
21
specchi sferici : dimostrazione
dimostrazione :
•
•
•
•
•
•
•
•
•
α ≈ PS / OS = PS / p ;
β ≈ PS / CS = PS / r ;
γ ≈ PS / IS = PS / i ;
OPC : α + θ + ( 180 - β ) = 180 ;
OPI : α + 2 θ + ( 180 - γ ) = 180 ;
2α+2θ=2β;
α+2θ= γ;
α=2β-γ;
α+γ=2β;
1/p+1/i=2/r
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
[... segue]
P
O
C
S
I
POC = α = ♦
PCI = β = ♦
PIS = γ = ♦
OS
=p;
CS
=r;
IS
=i;
OPC = CPI = θ.
♠
22
specchi sferici : equazione
[ ... segue ]
1/p+1/i=2/r;
" per def., se p → ∞ ⇒ i → f ;
" 0+1/f=2/r;
" f=r/2
[QED] ;
O
I
C
" 1/p+1/i=1/f.
NB. nella dim., non si usa la direzione
POC = α = ♦
dei raggi; pertanto, i ↔ p .
PCI = β = ♦
" i = f p / (p - f);
PIS = γ = ♦
" p < f ⇒ immagine virtuale;
OS
=p;
" p > f ⇒ immagine reale;
CS
=r;
" p = f ⇒ ??? ;
IS
=i.
" ingrandimento m = | i | / | p | . [no dim.]
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
P
S
♠
23
rifrazione su superfici sferiche
•
•
•
•
•
approssimazione : Q’ ≈ Q (cioè r grande, γ piccolo) ;
OPC : α + β + (180 - θ1) = 180 → α + β = θ1 ;
IPC : γ + θ2 + (180 - β) = 180 → γ + θ2 = β ;
n1 sin θ1 = n2 sin θ2 → θ1, θ2 piccoli → n1 θ1 ≈ n2 θ2 ;
[ ... segue ... ]
n1 (α + β) ≈ n2 (β - γ) → n1 α + n2 γ = β (n2 - n1)
θ1
n1
P
n2
θ2
β
α
O
Q’
p
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
Q
γ
C
r
I
i
♠
24
rifrazione su superfici sferiche (2)
• n1 α + n2 γ = β (n2 - n1) ;
• sin α ≈ α ≈ PQ / p ; sin β ≈ β ≈ PQ / r ; sin γ ≈ γ ≈ PQ / i ;
• n1 / p + n2 / i = (n2 - n1) / r ;
• la formula non dipende da α → tutti i raggi uscenti da O convergono in I ;
• noti i mezzi (n1, n2, r), p ↔ i ;
• non dipende dal verso dei raggi → oggetto e immagine possono scambiarsi.
θ1
n1
P
n2
θ2
β
α
O
Q’
p
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
Q
γ
C
r
I
i
♠
25
lenti sottili
• prendiamo n1 ≈ 1, n2 = n ;
• passaggio 1 → 2 :
1/p - n / i’ = ( n-1 ) / r1 ;
[“-”]
• passaggio 2 → 1 :
n / (i’+L) + 1/ i = (1 - n) / r2 ;
• L → 0 (“lente sottile”) ;
• n / i’ = 1/p - ( n-1 ) / r1 =
= (1 - n) / r2 - 1 / i ;
n1
P
O
n1
Q
C1 C2
p
i’
n2
r1
r2
I
i
L
• 1/p + 1/i = (n-1)(1/r1 - 1/r2);
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
26
equazioni delle lenti sottili
• 1/p + 1/i = (n-1)(1/r1 - 1/r2);
• p → ∞ ⇒ i → f (dist. focale);
" Equazione delle lenti sottili :
n1
n2
P
n1
Q
1 / p + 1 / i = 1 / f;
O
" Equazione dei costruttori di
lenti :
C1 C2
p
i’
r1
r2
I
i
L
1/ f = (n-1)(1/r1 - 1/r2) .
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
27
immagine di una lente
•
•
•
•
Ex. lente convergente con oggetto “lontano” ;
altri casi possibili (ex lenti divergenti) ;
“costruzione dei raggi” ;
ingrandimento m = | i | / p (in questo caso m > 1).
p
i
F2
O
I
F1
f
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
f
♠
28
microscopio
• due lenti : “obiettivo” + “oculare” ;
• l’immagine complessiva è virtuale e capovolta;
• ingrandimento globale m = m1 × m2 .
obiettivo
oculare
occhio
I
O
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
29
Fine parte 5
Paolo Bagnaia - CTF - 5 - Onde e oscillazioni
♠
30
Liquidi viscosi
! la viscosità;
! moti di liquidi viscosi;
! legge di Hagen-Poiseuille;
! moto turbolento;
! velocità di sedimentazione;
! legge di Stokes.
Paolo Bagnaia - CTF - 6 - seminari
♠
1
viscosità
→
→
v
F
A
→
s
F
v=0
F=ηAv/s:
" A = area di due lamine di liquido, poste a distanza s;
" v = velocità relativa delle lamine;
" η = coefficiente di viscosità del liquido (funzione anche di
temperatura, pressione);
" F = forza di viscosità (due forze uguali ed opposte sulle due lamine).
Paolo Bagnaia - CTF - 6 - seminari
♠
2
coefficiente di viscosità
• η si misura in N·m / (m2·m/s) = Pa·s;
• il valore varia con il tipo di liquido e la
temperatura; alcuni valori in tabella :
0°
1.8×10-3 Pa·s
olio motore
30°
200×10-3 Pa·s
20°
1.0×10-3 Pa·s
glicerina
20°
1500×10-3 Pa·s
100°
0.3×10-3 Pa·s
sangue
37°
4.0×10-3 Pa·s
aria
20°
0.018×10-3 Pa·s
plasma
37°
1.5×10-3 Pa·s
idrogeno
0°
0.009×10-3 Pa·s
alcool
20°
1.2×10-3 Pa·s
vapore
100°
0.013×10-3 Pa·s
acqua
Paolo Bagnaia - CTF - 6 - seminari
♠
3
legge di Bernoulli
[valida solo per liquidi non viscosi con η = 0]
S2,v2,
h2,p2
→
v
S1,v1,h1,p1
tubo di flusso
½ ρ v2 + ρ g h + p = costante;
Paolo Bagnaia - CTF - 6 - seminari
♠
4
moti di liquidi viscosi
• discutiamo il moto di un liquido incompressibile, viscoso (η ≠ 0) in un condotto
cilindrico piano di raggio R costante :
r
L
1
→
v
R
2
• a causa della simmetria cilindrica, possiamo discutere il moto del liquido,
considerando le forze tra “cilindretti” coassiali di altezza L, raggio di base r e
spessore infinitesimo dr ; a causa della viscosità :
v[r=R] = 0; v[r+dr] < v[r]; v[r=0] = vmax.
NB : usiamo “[ ]” per le dipendenze funzionali, “( )” nel solito modo algebrico;
chiamiamo v’[r] = dv/dr; v”[r] = d2v/dr2 → Fviscosa [r] = η S v / d = η 2πrL v’[r] ;
dv[r+dr]/dr = d [v + dv/dr · dr] / dr → v’[r+dr] = v’[r] + v”[r] · dr.
Paolo Bagnaia - CTF - 6 - seminari
♠
5
forze nei liquidi viscosi
r
L
1
→
v
R
2
• su ogni cilindretto agiscono le pressioni sulla superficie di base (2πrdr) e le
forze viscose del cilindretto più interno (r) e di quello più esterno (r + dr) :
Fpressione[lato 1] - Fpressione[lato 2] = Fviscosa[r] - Fviscosa[r+dr];
• (p1 - p2) 2πrdr = η 2πrL v’[r] - η 2π(r+dr)L v’[r+dr] ;
π, sviluppo di v’[r+dr] }
{ / 2π
• (p1 - p2) r dr = ηrLv’ - η(r+dr)Lv’ - η(r+dr)Lv” · dr ;
{+-rv’, trascurare dr2, / dr }
• (p1 - p2) r = -ηLv’ - ηrLv” = -ηL d [rv’] / dr ;
{separazione di variabili}
• (p1 - p2)
∫ r dr = -ηL ∫ d [rv’] → ½ (p1 - p2) r2 = -ηLr dv/dr + cost.
r=0 ⇒ dv/dr = 0 ⇒ cost. = 0 → ½ (p1 - p2) r2 = -ηLr dv/dr.
Paolo Bagnaia - CTF - 6 - seminari
{... continua ...}
♠
6
equazione dei liquidi viscosi
r
L
→
v
1
R
2
• ½ (p1 - p2) r2 = -ηLr dv/dr → (p1 - p2) r dr = - 2 ηL dv
• ½ (p1 - p2) (r2 - R2) = - 2 ηL v;
• v[r] = (p1 - p2) ·
(R2
-
r2)
/ (4ηL).
{integrare r = r ÷ R, v= v ÷ 0 }
v
v* = v[r=0] =
= (p1-p2) R2 / (4ηL)
v*
• notare :
" il calo di pressione (p1 - p2) / L;
" la dipendenza da η : v ~ 1/η ;
" l’andamento di v = v[r] → vedi
" NB : in un liquido ideale v[r] = cost.
Paolo Bagnaia - CTF - 6 - seminari
0
R r
♠
7
equazione di Hagen - Poiseuille
• v[r] = (p1 - p2) · (R2 - r2) / (4ηL);
• Q = dV/dt = ∫ v dS = ∫0
R
R
v[r] · 2πr dr = ∫0 (p1 - p2) · (R2 - r2) / (4ηL) · 2πr dr =
= 2π (p1 - p2) / (4ηL) · (R2 · ½ R2 - ¼ R4) = 2π (p1 - p2) / (4ηL) · ¼ R4 =
= π R4 (p1 - p2) / (8ηL)
{eq. di Hagen-Poiseuille}
• notare :
" Q ~ π R4 , nei liquidi ideali Q ~ π R2 (v = cost ⇒ Q ~ S);
" ∆p = ZQ, con Z = 8ηL / (π R4), analogo alle leggi di Ohm delle correnti elettriche;
" Q ~ 1/L (“impedenza di un condotto”);
" Q ~ 1/η (“impedenza di un condotto”);
→
v
Paolo Bagnaia - CTF - 6 - seminari
♠
8
moti turbolenti
• un liquido viscoso può scorrere in modo turbolento,
caratterizzato da vortici;
• l’equazione di Poiseuille non è più valida, il valore della
portata Q è minore, non si può più descrivere il moto in
modo matematicamente semplice;
• la turbolenza insorge spontaneamente per alti valori del
numero di Reynolds nR :
" v : velocità del liquido;
nR = vdρ / η
• esperienza :
Paolo Bagnaia - CTF - 6 - seminari
" d : diametro del condotto;
" ρ : densità;
" η : viscosità.
nR < 2000 → moto laminare;
nR > 2000 → moto turbolento;
♠
9
velocità di sedimentazione
• una sferetta di raggio r e densità
ρS, scende in un liquido di viscosità
η e di densità ρL (ρS > ρL) ;
→
v
• forza viscosa (“legge di Stokes”) :
Fviscosa = 6π ηrv ;
• bilancio totale delle forze (asse verso il basso) :
FTOT = ma = 4/3 π r3 ρSa = Fpeso - Farchimede - Fviscosa =
= 4/3 π r3 ρSg - 4/3 π r3 ρLg - 6π ηrv;
• a = g (1 - ρL/ ρS) - 9 ηv / ( 2 r2 ρS);
Paolo Bagnaia - CTF - 6 - seminari
[... continua ...]
♠ 10
velocità limite
• a = g (1 - ρL/ ρS) - 9 ηv / ( 2 r2 ρS);
• v[t=0] ≈ 0 → a[t=0] > 0 → v aumenta ...
• vlimite = v[a=0] = 2 r2g (ρS - ρL) / (9 η)
v
!
!
!
!
0
Paolo Bagnaia - CTF - 6 - seminari
v=gt;
v = gt(1-ρL/ρS) ;
vlimite ;
v[t].
t
♠ 11
Gas reali
! gas perfetto e gas reali;
! equazione di van der Waals;
! diagrammi di fase.
Paolo Bagnaia - CTF - 6 - seminari
♠ 12
il “gas perfetto”
1. sistema termodinamico costituito da N
molecole;
2. molecole in moto casuale, isotropo,
governato dalle leggi degli urti;
3. il numero N è grande (~ NA), le
fluttuazioni statistiche sono trascurabili;
4. il volume proprio occupato dalle
molecole è piccolo rispetto al volume
totale del recipiente;
5. le molecole non sono soggette ad altre
interazioni, oltre gli urti elastici tra loro,
e con le pareti del recipiente.
Paolo Bagnaia - CTF - 6 - seminari
pV = nRT
♠ 13
i gas reali - volume proprio
4.
(...)
il volume proprio occupato dalle molecole è piccolo rispetto al volume
totale del gas;
(...)
sostituire :
4’) ogni molecola occupa un certo volume,
( ex. rm = raggio tipico → Vm = 4/3 π rm3,
Vmole ≡ b = NA Vm = 4/3 π NA rm3 );
ex. rm=2.5×10-10 m → b = 4×10-5 m3/mole = 4×10-2 l/mole,
da confrontare (T=300K, p=1 atm) con V=22.6 l/mole.
nell’equazione di stato V → V’ = V - nb
(importante a piccolo V)
Paolo Bagnaia - CTF - 6 - seminari
♠ 14
i gas reali - forze intermolecolari
5.
(...)
le molecole non sono soggette ad altre interazioni, oltre gli urti elastici
tra loro, e con le pareti del recipiente.
5’) esistono forze intermolecolari attrattive;
esse aumentano la “pressione efficace”
in funzione della densità :
[ogni molecola sente una forza ~ al numero di molecole
che ha in un piccolo intorno, i.e. ~ N/V; inoltre, il numero
di molecole che si trovano in tale situazione è anche
esso ~ N/V; in totale, effetto ~ (N/V)2, cioè ~ (n/V)2 ]
nell’equazione di stato p → p’ = p + a(n/V)2
(importante ad alta densità, i.e. alto n e/o piccolo V)
Paolo Bagnaia - CTF - 6 - seminari
♠ 15
equazione di stato dei gas reali
• equazione dei gas reali (di van der Waals) :
•
•
•
•
•
•
(p + a n2 / V2) (V - nb) = n R T
p : pressione del gas;
V : volume occupato;
n : numero di moli (= nmolecole / NA, oppure m / mmolare);
R : 8.31 J / (mol K), costante dei gas perfetti;
T : temperatura in gradi Kelvin (= C + 273.16°);
a,b : parametri dei gas reali, da determinare
sperimentalmente per ogni gas.
Paolo Bagnaia - CTF - 6 - seminari
♠ 16
p [10 5 Pa]
500
500 K,
gas perfetto
CO2
n = 1 mole
400
300
500 K
200
344 K
100
304 K
b
T=264 K
0
0
Paolo Bagnaia - CTF - 6 - seminari
100
200
300
V (cm3)
400
♠ 17
diagrammi di fase
• nel piano pT si scrivono le linee
di separazione tra le fasi di un
corpo
p
(acqua)
— sublimazione
— fusione
— evaporazione
• differente per ogni sostanza,
ex. ~ acqua (scala ~ log);
• lungo le linee coesistono due
fasi;
• A : punto triplo (i.e. le tre fasi
possono coesistere);
pC
• C : punto critico (per T>TC, non
c’è più liquido, solo gas);
p0
pA
• l’acqua ha pendenza differente
dagli altri materiali;
- - - p0 = 1 atm.
Paolo Bagnaia - CTF - 6 - seminari
liquido
solido
C
gas
A
vapore
TA
TC
T
♠ 18
Fine
Paolo Bagnaia - CTF - 6 - seminari
♠
19
Esercizi di Fisica
Paolo Bagnaia
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
!
!
!
!
!
!
!
!
!
!
Cinematica
Meccanica del punto
Meccanica dei sistemi
Meccanica dei fluidi
Termologia
Termodinamica
Elettrostatica
Correnti continue
Campo magnetico
Ottica.
♠
1
Alcune avvertenze
1. Queste note sono il testo degli esercizi svolti a lezione, con una breve traccia delle
soluzioni. Quindi non sostituiscono né un buon libro di esercizi, né le lezioni in aula.
2. La soluzione serve come controllo dello svolgimento autonomo elaborato dallo
studente. Non è molto utile guardarla subito dopo avere letto il testo, senza provare a
risolvere l’esercizio senza aiuto esterno.
3. Il livello degli esercizi è molto semplice, adatto ad una prima comprensione degli
argomenti. Il livello degli esercizi d’esame è un po’ più difficile. Esiste anche una
raccolta degli esercizi d’esame degli ultimi anni (rivolgersi all’ufficio dispense del
Dipartimento di Fisica, Edificio Fermi, piano terreno).
4. È buona norma risolvere un esercizio in modo simbolico, utilizzando lettere al posto
dei valori numerici (ex. “v” per velocità, “m” per massa, etc.). Una volta ottenuta la
soluzione, si potrà così controllare la correttezza delle dimensioni e la plausibilità del
risultato. Poi si otterrà la soluzione numerica, sostituendo i valori dei dati.
5. Talvolta i dati non usano sistemi di misura omogenei (ex. la velocità in Km/h e lo
spazio in m). In questo caso è bene fare subito le “equivalenze”, passando ad un
unico sistema di misura.
P.B., Roma, Gennaio 2002.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
2
Cinematica
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠
3
Esercizi presi da Halliday-Resnick-Walker / Serway
notazione : “HRW capitolo [esercizi]” oppure “S capitolo [esercizi]”
" CINEMATICA :
HRW 2 [1E, 3E, 9P, 11P, 13P, 19P, 29P, 33E, 35E, 37E, 39E, 41E, 43E, 47P,
49P, 51P, 55P, 57P, 61E, 63E, 65E, 67E, 71P, 77P, 79P, 83P, 85P, 89P],
HRW 3 [1E, 3E, 5P, 9E, 11E, 15P, 19E, 21E, 27P, 29P, 31P], HRW 4 [5E, 9E,
19E, 21E, 23E, 25E, 27E, 31E, 37P, 41P, 47P, 51E, 53E, 55E, 57E, 59E, 61P,
65P, 67E, 69E, 73E, 75P, 77P, 81P], S 1 [33, 35, 37, 39, 41, 49], S 2 [1,
7,9,11, 13, 17, 21, 23, 25, 29, 33, 35, 37, 43, 47], S 3 [3, 5, 7, 9, 11, 13, 15,
17, 19, 25, 27, 29, 31, 35, 37, 39, 41, 55].
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
4
Esercizio – Un’automobile viaggia per un certo tempo T alla velocità di 40
Km/h e poi per lo stesso tempo alla velocità di 80 km/h. Trovare la velocità
media.
————————————
Soluzione –
La velocità media si ottiene dalla definizione :
vm =
stot v1T + v 2T v1 + v 2
=
= 60 Km / h.
=
Ttot
T +T
2
Non è necessario (ma non è neppure sbagliato) trasformare da Km/h a m/s.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠
5
Esercizio – Un’automobile viaggia per un certo tempo T alla velocità di 40
Km/h, percorrendo un cammino S, e poi per lo stesso tragitto alla velocità di
80 km/h. Trovare la velocità media.
————————————
Soluzione –
La velocità media si ottiene dalla definizione :
vm =
=
NB –
stot
S +S
2
=
=
=
Ttot S / v1 + S / v 2 1/ v1 + 1/ v 2
2
2 v1 ⋅ v 2 2 ⋅ 40 ⋅ 80
= 53.3 Km / h.
=
=
(v1 + v 2 ) /(v1 ⋅ v 2 ) v1 + v 2
40 + 80
1. È differente dal caso precedente (capire bene !!!);
2. Non occorre trasformare da Km/h a m/s.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠
6
Esercizio – Una barca naviga controcorrente dal punto A al punto B alla
velocità costante v1 = 10 Km/h rispetto alla riva. Successivamente torna
indietro alla velocità v2 = 16 Km/h rispetto alla riva. Sapendo che il motore
della barca ha lavorato al massimo della potenza in entrambi i percorsi,
trovare la velocità della corrente e la velocità della barca rispetto alla corrente.
————————————
Soluzione –
La velocità della barca rispetto alla corrente (chiamata u) è la stessa nei due
casi. Nel primo caso la velocità della corrente (chiamata w) si sottrae dalla
velocità della barca, nel secondo si somma :
v1 = u − w ;
v 2 = u + w;
B
barca (u)
A
v +v
u = 1 2 = 13 Km / h;
2
fiume (w)
v 2 + v1
= 3 Km / h.
2
NB – Non c’è nessun bisogno di trasformare da Km/h a m/s, ma non è vietato.
w=
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠
7
Esercizio – Stessa situazione del caso precedente. Sono note la velocità
della corrente (w=2Km/h) e la velocità della barca rispetto alla corrente
(u=10Km/h). Calcolare la velocità media della barca.
————————————
Soluzione – Definendo S la distanza tra A e B, la barca compie un tragitto
totale 2S. Il tempo totale è facile da calcolare :
vm =
stot
S +S
S +S
=
=
=
Ttot S / v1 + S / v 2 S /(u + w ) + S /(u − w )
2
2(u 2 − v 2 ) u 2 − v 2 100 − 4
=
=
= 9.6 Km / h.
=
=
u
1/(u + w ) + 1/(u − w ) u − v + u + v
10
B
barca (u)
A
fiume (w)
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠
8
Esercizio – Un’automobile, durante una frenata uniforme, passa in un minuto
dalla velocità di 40 Km/h a quella di 28 Km/h. Trovare il valore della
accelerazione e lo spazio percorso.
————————————
Soluzione –
v1 = 40 Km/h = 11.11 m/s; v2 = 28 Km/h = 7.78 m/s;
a = (v2 -v1 ) / ∆t = (7.78 - 11.11) / 60 = - 0.055
[quale è il significato del segno “-” ???]
m/s2;
v1
v2
∆t
s = 1/2 a ∆t2 + v1 ∆t = - 0.5 · 0.055 · 602 + 7.78 · 60 = - 100 + 666.6 = 566.6 m.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠
9
Esercizio – Un treno si muove tra due stazioni, poste ad 1.5 Km di distanza.
Percorre la prima metà del tragitto di moto uniformemente accelerato e la
seconda di moto uniformemente ritardato. Data la velocità massima (50Km/h),
calcolare il valore dell’accelerazione e il tempo totale di percorrenza.
————————————
Soluzione – È sufficiente mettere a sistema le equazioni dello spazio e della
velocità, e poi risolvere per T, a; prima bisogna trasformare la velocità in m/s :
v max
 50 × 103 
 = 13.88 m / s;
= 
3
 3.6 × 10 
d 1  T 2
 = a  ;
2 2  2 

T

v
a
;
=
 max
2

2

  T  v max
v max
13.882
2
;
=
m
s
a
0
.
128
/
;
=
=
=



 2 
3
a
d
1.5 × 10


⇒ 
⇒ 
2v max
1 2
d

v
T
;
=
=
= 217 s = 3 min 37 s.
 2 2a max

a


Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 10
Esercizio [S 2.39] – In una gara sui 100 m, due atleti impiegano lo stesso
tempo di 10.2 s. Il primo impiega 2 s in accelerazione costante, poi mantiene
la velocità costante fino alla fine, mentre il secondo accelera per 3 s, poi
mantiene la velocità costante. Determinare per ciascun concorrente
l’accelerazione e la velocità massima.
————————————
Soluzione –
Primo concorrente :
½ a1 t12 + a1t1 (T - t1) = stot ⇒
a1 = stot / (½ t12 + t1 T - t12) = stot / (t1 T - ½ t12) =
= 100 / (2 · 10.2 - 0.5 · 22) = 5.43 m/s2;
v1 = a1t1 = 5.43 · 2 = 10.86 m/s;
Secondo concorrente : ½ a2 t22 + a2t2 (T - t2) = stot ⇒
a2 = stot / (½ t22 + t2 T - t22) = stot / (t2 T - ½ t22) =
= 100 / (3 · 10.2 - 0.5 · 32) = 3.83 m/s2;
v2 = a2t2 = 3.83 · 3 = 11.5 m/s.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 11
Esercizio [S 2.39 parte 2] – Nella stessa gara dell’es. precedente, quale
concorrente si trova in testa dopo un tempo di 6 secondi ?
————————————
Soluzione –
Primo concorrente :
s1 = ½ a1 t12 + a1t1 (t* - t1) =
= 0.5 · 5.43 · 22 + 5.43 · 2 · (6 - 2) = 54.3 m;
Secondo concorrente : s2 = ½ a2 t22 + a2t2 (t* - t2) =
= 0.5 · 3.83 · 32 + 3.83 · 3 · (6 - 3) = 51.7 m;
È in testa il primo concorrente di una distanza d = 54.3 - 51.7 = 2.6 m.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 12
Esercizio – Un’automobile viaggia a 120 Km/h. Visto un ostacolo, il
conducente riesce a fermarsi in 110 m. Quale è l’accelerazione e quanto
tempo impiega ?
————————————
Soluzione –
vo = 120 Km/h = 33.3 m/s;
s = vo T - 1/2 a T2 ;
vfin = 0 = vo - aT
⇒
T = vo / a; s = vo2 / a - 1/2 vo2 / a = 1/2 vo2 / a ⇒
a = vo2 / 2 s = 33.32 / (2 · 110) = 5.040 m / s2 ;
T = vo / a = 33.3 / 5.040 = 6.60 sec.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 13
Esercizio – Una palla viene lanciata da terra verso l’alto con velocità iniziale
di 12 m/s.
a) Quanto tempo impiega a raggiungere il punto più alto della traiettoria ?
b) Quanto vale la distanza da terra del punto più alto ?
c) Dopo quanto tempo ricade a terra ?
d) Con che velocità la palla tocca terra ?
e) Quanto vale lo spazio totale percorso dalla palla ?
————————————
Soluzione –
a) vf - vi = gt ⇒ t = (vf - vi) / g = (0 - 12) / (-9.8) = 1.24 s;
b) s = - 1/2 g t2 + vi t = -0.5 · 9.8 · 1.242 + 12 · 1.24 = 7.3 m;
c) t2 = t [perché ???];
d) vterra = vi = 12 m/s [perché ???];
e) stot = 2s = 14.6 m.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 14
Esercizio [S 2.27] – Un oggetto viene lanciato da terra ad un’altezza di 4 m. Il
tragitto dura 1.5 s. Determinare la velocità dell’oggetto :
a) al momento del lancio;
b) all’istante di arrivo.
————————————
Soluzione –
a) h = vo t - ½ g t2 ⇒ vo = (h + ½ g t2) / t = (4 + 0.5 · 9.8 · 1.52) / 1.5 = 10 m/s
b) vfin = vo - g t = 10 - 9.8 · 1.5 = - 4.70 m/s;
y
che significa “-” 4.70 m/s ? (l’oggetto sta ricadendo).
h
x
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 15
Esercizio – Un uomo lancia un sasso dal tetto di un palazzo verso l’alto, con
una velocità di 12.25 m/s. Il sasso raggiunge il suolo dopo 4.25 s. Si calcoli :
a) l’altezza del palazzo;
b) la massima altezza raggiunta dal sasso;
c) la velocità con cui il sasso tocca il suolo.
————————————
Soluzione –
a) y = h + vot - ½ gt2 ;
y = 0 ⇒ h= ½ gt2 - vot = 0.5·9.8·4.252 - 12.25·4.25 =36.4 m;
b) v(t) = vo - gt ;
v(t) = 0 ⇒ t* = vo/g ; y
y(t*) = h + vo2/g - ½ vo2/g = h + ½ vo2/g =
= 36.4 + 0.5 · 12.252 · / 9.8 = 44.1 m;
max =
c) vsuolo = vo - gtsuolo = 12.25 - 9.8 · 4.25 = -29.4 m/s [che vuol dire “-” ?].
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 16
Esercizio – Una barca naviga in un fiume, che ha una corrente di 1 m/s. Il suo
motore è in grado di produrre una velocità di 2 m/s rispetto alla corrente.
Trovare la velocità della barca rispetto alla riva in tre casi :
a) barca in favore di corrente;
b) barca contro corrente;
c) barca che naviga a 90° rispetto alla corrente.
————————————
Soluzione a) v1 = u + w = 3 m / s;
b) v 2 = u − w = 1 m / s;
c ) v 3 = u 2 + v 2 = 5 = 2.23 m / s.
v
v3
u
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 17
Esercizio – Una barca a motore si dirige a 7.2 Km/h, in direzione
perpendicolare alla riva. Però la corrente la fa approdare a 150 m più a valle
di un fiume largo 500 m. Trovare la velocità della corrente e il tempo totale di
attraversamento del fiume.
————————————
Soluzione – I moti lungo gli assi sono indipendenti, ma durano lo stesso
tempo totale T. Pertanto :
vy = vmotore = 7.2 Km/h = 2 m/s;
vy = vmotore = s / T ⇒ T = s / vy = 500 / 2 = 250 s = 4 min 10 s;
vx = vcorrente = d/T = 150 / 250 = 0.6 m/s.
d
y
fiume
s
x
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
B
A
♠ 18
Esercizio – Un oggetto viene lanciato da una torre, alta 25 m, in direzione
orizzontale, con velocità 15 m/s. A che distanza cade, rispetto al bordo della
torre ? In quanto tempo ?
————————————
Soluzione –
in orizzontale : x = vx t;
in verticale :
y
y = h - ½ g t2;
di conseguenza : y = h - ½ g (x/vx)2
h
y=0 ⇒ h = ½ g (x1/vx)2 ⇒ x12 = 2 h vx2 / g ⇒
x1 = vx (2 h / g) ½ = 15 (2 · 25 / 9.8) ½ = 33.9 m;
x1
x
t = x1 / vx = 33.9 / 15 = 2.26 s.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 19
Esercizio – Un cannone spara un proiettile alla velocità di 100 m/s. Si calcoli
l’angolo rispetto al piano orizzontale che causa la gittata massima e il valore
della gittata. Si calcoli inoltre l’angolo necessario per colpire un bersaglio a
500 m di distanza.
————————————
Soluzione –
y



x = vT cosϑ
T = x /(v cosϑ )

vo


⇒

 y = vT sinϑ − 1 gT 2

gx 2
1
2
;
ϑ
 y = x tanϑ − 2 2

2

v cos ϑ

x
sinϑ 2v 2 cos2 ϑ 2v 2 sinϑ cosϑ v 2 sin 2ϑ
y = 0 ⇒ x = 0 oppure x =
;
=
=
g
g
g
cosϑ
gittata max per sin(2ϑ) = 1 ⇒ ϑ = 45° ⇒ ymax = v2/g = 1020 m;
d = v2sin(2ϑ)/g ⇒
ϑ = asin(gd/v2)/2 = asin(9.8·500/1002)/2 = asin(0.49)/2 =
= 14° 40’ 13” (o 59° 40’ 13”) [perché 2 sol. ???]
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 20
Esercizio – Trovare la velocità angolare nei seguenti casi :
a) la Terra che ruota attorno al Sole (supporre il moto circolare uniforme);
b) la Terra che ruota attorno a se stessa;
c) la lancetta delle ore;
d) la lancetta dei minuti;
e) la lancetta dei secondi.
————————————
Soluzione –
a) ω1 = 2π / T1 = 2π / (365 · 24 · 60 · 60) = 1.99 · 10-7 rad/s;
b) ω2 = 2π / T2 = 2π / (24 · 60 · 60) = 7.27 · 10-5 rad/s;
c) ω3 = 2π / T3 = 2π / (12 · 60 · 60) = 1.45 · 10-4 rad/s;
d) ω4 = 2π / T4 = 2π / (60 · 60) = 1.7 · 10-3 rad/s;
e) ω5 = 2π / T5 = 2π / 60 = 0.104 rad/s.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 21
Esercizio – Determinare la velocità e la velocità angolare che deve
mantenere un aeroplano all’equatore affinché il sole appaia fisso all’orizzonte.
L’aereo deve volare verso est o verso ovest ?
————————————
Soluzione –
ωaereo = - ωTerra = 7.27 · 10-5 rad/sec (vedi esercizio precedente);
il segno “-” significa che l’aereo deve andare da est verso ovest;
vaereo = ω · rTerra = 7.27 · 10-5 · 6.37 · 106 = 463 m/s = 1670 Km/h.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 22
Esercizio – Un treno, affrontando una curva di raggio 150 m, nei 15 s che
impiega a percorrere la curva rallenta da 90 Km/h a 50 Km/h. Calcolare
l’accelerazione tangenziale e normale nel momento in cui la velocità è 50
Km/h, assumendo che il treno continui a decelerare.
————————————
Soluzione –
a) trasformiamo da Km/h a m/s :
v1 = 90 Km/h = 25.0 m/s; v2 = 50 Km/h = 13.9 m/s;
b) l’accelerazione tangenziale : aTmedia = (v2 - v1) / T = -0.74 m/s 2;
c) accelerazione radiale : aRcentripeta = v22 / r = 1.29 m/s2;
d) accelerazione totale (modulo), poiché aT e aR sono ortogonali :
atot = aT2 + aR2 = ( −0.74)2 + 1.292 = 1.49 m / s 2 .
NB – se il treno non continuasse a decelerare, aT=0, atot=aR.
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 23
Fine
Paolo Bagnaia - CTF - 1a - Esercizi di cinematica
♠ 24
Meccanica del
punto
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠
1
Esercizi presi da Halliday-Resnick-Walker / Serway
notazione : “HRW capitolo [esercizi]” oppure “S capitolo [esercizi]”
! MECCANICA DEL PUNTO E DEI SISTEMI
HRW 5 [5E, 7E, 9E, 11P, 13E, 15E, 17E, 19E, 23E, 25E, 27E, 29E, 31E, 33P,
35P, 41P, 43P, 45P, 47P, 51P, 57P, 63P], HRW 6 [1E, 3E, 7E, 9E, 11E, 15E,
17P, 21P(*), 25P, 33P, 35P, 37P(*), 39P(*), 45E, 49E, 51E, 53E, 57E, 59P, 65P],
HRW 7 [1E, 7P, 9E, 11E, 19P, 21E, 25P, 27E, 35E, 37P, 41E, 43E, 45P, 47P,
49P], HRW 8 [1E,3E, 5E, 7P, 11E, 13E, 15P, 17P, 19P, 37P, 41E, 45E, 47P,
49P, 51P], HRW 9 [1E, 3E, 7P, 13E, 17P, 19P, 21E, 23P, 31P, 33P], HRW 10
[1E, 3E, 5E, 13P, 21P, 29E, 31E, 33E, 41E, 45E, 49P, 51P, 55P], HRW 14 [1E,
3E, 7E, 19E], HRW 16 [1E, 5E, 7E, 13E, 17P, 19P, 25P, 51E, 53E], S 4 [3, 7, 9,
13, 17, 27, 29, 31, 33, 37, 39], S 5 [1, 3, 5, 7, 9, 11, 13, 15, 17, 21, 23, 27, 35,
39, 41, 45, 47, 49, 51], S 6 [1, 3, 7, 9, 13, 15, 17, 19, 21, 23, 25, 27, 29, 33, 35,
37, 39, 43, 49], S 7 [1, 3, 5, 7, 9, 11, 15, 21, 23, 29, 41, 43], S 8 [1, 3, 5, 7, 9, 13,
15, 17, 21, 23, 45, 51], S 11 [1, 3, 5, 11], S 12 [1, 3, 5, 9, 11, 19, 33, 37].
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
2
Esercizio – Un filo di ferro si spezza ad una tensione massima di 4400 N.
Quale accelerazione massima verso l’alto può imprimere ad un oggetto di 400
Kg ?
————————————
Soluzione –
Per il corpo :
pertanto :
ma = T – mg;
T = m (a + g) ⇒ Tmax = m (amax + g) ⇒
amax = Tmax /m – g = 4400 / 400 – 9.8 = 1.2 m/s2.
T
mg
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
m
♠
3
Esercizio – Una fune, collegata ad una carrucola, connette due masse
identiche, una delle quali è libera di muoversi su un piano inclinato di angolo ϑ
(ϑ = 30°), mentre l’altra penzola nel vuoto. Calcolare l’accelerazione su
entrambe le masse.
————————————
Soluzione –
L’accelerazione è identica per entrambe le masse. Il bilancio delle forze dà :
(m1 + m2) a = m2 g – m1 g sin ϑ ⇒ m1 = m2 = m ⇒
a = m g (1 – sin ϑ) / (2m) = g (1 – sin ϑ) / 2 = 9.8 × (1 - 0.5) / 2 = 2.45 m/s2;
l’accelerazione è diretta verso il basso per
la massa libera e verso l’alto del piano per
quella sul piano inclinato.
m
ϑ
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
aaaaa
m
♠
4
Esercizio – Un corpo scivola senza attrito su un piano inclinato di angolo 30°,
lungo 40 m, partendo da fermo. Determinare il tempo totale del tragitto e la
velocità finale.
————————————
Soluzione –
a = g sinϑ;
L = ½ a t2 = ½ g sinϑ t2 ⇒ t = [2 L / (g sinϑ)]½ = 4.04 s;
v = a t = g sinϑ t = 19.8 m/s.
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠
5
Esercizio – [stesso esercizio del caso precedente] C’è un attrito dinamico, di
coefficiente kd = 0.5. Determinare il tempo totale del tragitto e la velocità finale.
————————————
Soluzione –
ma = m g sin ϑ - k m g cos ϑ ⇒ a = g sinϑ - kg cos ϑ = g (sinϑ - k cos ϑ);
L = ½ a t2 = ½ (g sinϑ - k cos ϑ) t2 ⇒ t = [2 L / (gsinϑ - kgcos ϑ)]½ = 11.03 s;
v = a t = g (sinϑ - k cos ϑ) t = 7.24 m/s.
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠
6
Esercizio – [stesso esercizio del caso precedente, senza attrito] Al termine
del piano inclinato [senza attrito] c’è un tratto piano, con attrito dinamico di
coefficiente kd = 0.25. Determinare la distanza percorsa dal corpo sul tratto
piano del tragitto e il tempo impiegato prima di fermarsi.
————————————
Soluzione –
ma = F = -k m g ⇒ a = -k g;
v(t) = vo - k g t ⇒ tfin = vo / k g = 8.08 s;
Ltot = vo tfin + ½ a tfin2 = vo tfin - ½ k g tfin2 = 80 m.
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠
7
Esercizio – Trovare il lavoro necessario per portare un corpo di massa 2 Kg
dalla velocità di 2 m/s a quella di 5 m/s.
————————————
Soluzione –
L = ½ m vfin2 - ½ m vini2 = 0.5 × 2 × (52 - 22) = 21 J.
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠
8
Esercizio – Trovare il lavoro necessario a fermare un corpo di massa 2 Kg,
che procede alla velocità di 8 m/s.
————————————
Soluzione –
L = - ½ m vini2 = - 0.5 × 2 × 82 = - 64 J.
[perché “-” ?]
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠
9
Esercizio – Un carrello di massa 100 Kg
compie il percorso indicato in figura, passando
dal punto A al punto C. Nota la velocità iniziale
(vA=0) e le differenze di quota tra A e B (a=20
m) e tra C e B (c=18m), calcolare il valore
dell’energia potenziale in A e della velocità in B
e in C.
————————————
C
A
a
c
B
Soluzione – Scegliamo la costante dell’energia potenziale in modo che
EpotB=0. In tal caso :
EpotA = m g a = 100 × 9.8 × 20 = 19600 J;
EpotA + ½ m vA2 = EpotB + ½ m vB2 = mga = ½ m vB2 ⇒
vB2 = 2 g a ⇒ vB = (2 × 9.8 × 20)½ = 19.8 m/s;
m g a = ½ m vC2 + mgc ⇒
vC2 = 2 g (a - c) ⇒ vC = [2 × 9.8 × (20-18)]½ = 6.26 m/s.
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 10
Esercizio – Un corpo di massa 2 Kg cade dall’altezza di 2 m su una molla di
costante elastica 200 N/m. Di quanto si abbassa la molla ? Dopo un po’, le
oscillazioni si smorzano. Dove è il punto di riposo della molla ?
————————————
Soluzione – Si può scrivere : mgh = ½ k d2 ⇒ d2 = 2mgh / k; no ! sbagliato !
mg (h + d) = ½ k d2 ⇒ k d2 - 2mgd - 2mgh = 0 ⇒
mg ± m 2g 2 + 2kmgh mg 
2kh 
d=
=
 1 ± 1 +

k
k 
mg 
d=
scegliere il segno "+ " [perche' ?]
mg 
2 × 200 × 2 
2kh  2 × 9.8 
1 + 1 +
 1 + 1 +
 = 0.73 m
 =
k 
mg 
2 × 9.8 
200 
Il punto di riposo si ottiene da : mg = kb ⇒ b = mg/k = 2 ×9.8 / 200 = 9.8 cm.
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 11
Esercizio – Un trattore di massa 1200 Kg percorre una salita di pendenza
30°; il motore eroga una potenza di 9800 W. Calcolare la velocità massima
disponibile.
————————————
Soluzione –
In un tempo t :
L = W t = m g h=m g s sinϑ ⇒
s / t = v = W / (m g sinϑ) = 9800 / (1200 × 9.8 ×0.5) = 1.67 m/s = 6 Km/h.
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 12
Meccanica dei
sistemi
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 13
Esercizio – Una pallina di massa 1 Kg urta alla velocità di 1 cm/s una
seconda pallina ferma, di massa 2 Kg. Dopo l’urto, le palline si appiccicano.
Trovare la loro velocità e la viariazione di energia cinetica nell’urto.
————————————
Soluzione –
m1vini = (m1 + m2) vfin ⇒
vfin = vini × m1 / (m1 + m2) = .01 × 1 / (1 + 2) = 0.33 cm/s;
∆T = Tfin - Tini = ½(m1 + m2) vfin2 - ½ m1 vini2 =
= 0.5 ×(1000 + 2000) × 0.332 - 0.5 × 1000 × 12 = -333 erg;
[perché “-” ???]
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 14
Esercizio – Un corpo di massa 20 Kg è attaccato con una fune lunga 4 m.
Una pallottola di massa 50 g lo urta, restandovi conficcata. Il corpo percorre
un angolo di 30°. Trovare la velocità iniziale della pallottola.
————————————
Soluzione –
Nel primo urto anelastico vale : mv = (M+m)w ⇒ w = v m / (M+m)
ϑ
L’energia cinetica dei due corpi si converte poi in energia potenziale :
½(M+m)w2 = ½(M+m) v2 m2 / (M+m)2 = ½ m2 v2 / (M+m) =
R
= (M+m) g h = (M+m) g R (1 - cos ϑ) ⇒
v2
=2
v=
(M+m)2
g R (1 - cos ϑ) /
m2
⇒
h
M +m
20 + 0.050
2 × 9.8 × 4 × (1 − cos 30! ) = 1300m / s.
2gR(1 − cosϑ ) =
m
0.050
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 15
Esercizio – Un corpo di massa 20 Kg è attaccato con una fune lunga 4 m.
Una pallottola di massa 50 g, che procede alla velocità di 1000 m/s, lo urta,
perforandolo, e proseguendo alla velocità di 300 m/s. Trovare l’angolo di cui si
alza il corpo.
————————————
Soluzione –
Nel primo urto anelastico vale : mv = MW +mw ⇒
ϑ
W = m (v - w) / M = 1.75 m/s;
L’energia cinetica del corpo si converte poi in energia potenziale :
½MW2 = M g h = M g R (1 - cos ϑ) ⇒
R
h
1 - cos ϑ = ½ W2 / (gR) ⇒
gR − 12 W 2 9.8 × 4 − 0.5 × 1.752
= 0.961 ⇒ ϑ ≈ 16!
=
cosϑ =
gR
9.8 × 4
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 16
Esercizio – Una sbarra di massa trascurabile e lunghezza 50 cm è attaccata
agli estremi con due elastici, di costanti 200 N/m e 300 N/m rispettivamente. In
quale punto della sbarra bisogna porre un corpo puntiforme di massa 5 Kg, in
modo che la sbarra rimanga orizzontale ? Di quanto si allungano gli elastici ?
————————————
Soluzione – Se la sbarra è orizzontale, l’allungamento
di entrambi gli elastici è identico (chiamiamolo d); le
forze sono k1d e k2d. Affinché la sbarra rimanga ferma,
occorre che il momento totale delle forze sia nullo.
Calcolando il momento rispetto al punto in cui è posto il
d
corpo, si ha (notare i segni +-) :
k2
k1
k1dx - k2d(L-x) + mg·0 = 0 ⇒
x = k2dL / (k1d + k2d) = k2L / (k1 + k2) = 30 cm;
m
x
L’allungamento si ottiene ponendo la somma vettoriale
L
delle forze uguale a zero (asse positivo verso l’alto) :
k1d + k2d – mg = 0 ⇒ d = mg / (k1 + k2) = 9.8 cm.
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 17
Esercizio – Una bilancia a statera (vedi figura) di massa trascurabile ha la
massa scorrevole (m) di 500 g, il braccio del piatto (a) di 40 cm. Quando una
certa massa M é posta sul piatto, l’equilibrio richiede che la massa m venga
posta a 20 cm dal punto di sospensione. Quanto segna la bilancia ?
b
a
m
M
————————————
Soluzione –
Eguagliamo a zero il momento totale delle forze :
Mga - mgb = 0 ⇒ M = mb / a = 500 × 20 / 40 = 250 g.
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 18
Esercizio – Una sbarra di massa trascurabile e lunghezza 2 m è fissata al
centro e libera di ruotare. Ha alle estremità due masse, rispettivamente di 80
Kg e 60 Kg. Dove bisogna mettere una terza massa, di 30 Kg, in modo che la
sbarra resti orizzontale ?
————————————
Soluzione –
Eguagliamo a zero il momento totale, calcolato rispetto al punto centrale
(fulcro) :
m1gL/2 – m2gL/2 – m3gx = 0 ⇒
x = (m1L/2 – m2L/2) / m3 = L/2 (m1 – m2) / m3 = 66 cm.
x
m1
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
m3
m2
♠ 19
Esercizio – Trovare il raggio dell’orbita di un corpo che percorre un’orbita
circolare geostazionaria [dati raggio terrestre : 6.37 × 106 m].
————————————
Soluzione – Si eguaglia la forza di gravità a quella necessaria per un moto
circolare uniforme; si impone inoltre che la velocità angolare sia la stessa
della rotazione terrestre :
mT m
mT mRT2
mRT2
mv 2
= G 2 =G 2 ⋅ 2 = g 2 ;
R
R
RT R
R
v=
2πR
⇒
T
2
gRT2T 2
RT2
4π 2R 2
 2πR 
2
3
v =
=g
⇒R =
⇒
 =
2
2
R
T
4π
 T 
2 2
6
2
gR
T
×
×
⋅
×
9
.
8
(
6
.
37
10
24
3600
)
3
T
3
R=3
Km
=
=
×
42
.
2
10
2
2
4π
4π
NB - L’orbita non deve necessariamente essere tutta al di sopra dell’equatore;
deve però avere come centro il centro della Terra [perché ???].
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 20
Esercizio – Determinare la velocità di un corpo che, senza usare alcun
motore, gira attorno alla Terra ad una quota di 100 m sul livello del mare.
Trascurare la resistenza dell’aria e approssimare la Terra con una sfera
perfetta di raggio RT = 6.37 × 106 m.
————————————
Soluzione –
Si eguaglia la forza peso subita dal corpo con la forza centripeta necessaria a
compiere il moto in questione :
mv 2
mv 2
mg =
=
⇒
R
RT + h
v = g (RT + h) = 9.8 ⋅ (6.37 ⋅ 106 + 102 ) = 7.9 ⋅ 103 m / s
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 21
Esercizio – Partendo da fermo, un motociclista
compie il percorso indicato in figura, composto da
un tratto in discesa e da una circonferenza di
A
h
raggio 4 m. Trascurando gli attriti, trovare il valore
minimo della quota h, affinché il percorso riesca. In
R B
tale ipotesi, trovare la velocità del motociclista nei
punti più alto e più basso della circonferenza.
————————————
Soluzione – Il punto critico è quello chiamato “A” nella figura; in A, per
mantenere la traiettoria circolare, l’accelerazione di gravità deve essere al più
uguale a quella richiesta dal moto circolare uniforme (g ≤ vA2/R). Pertanto :
1 mv 2
A
2
1 +
2
+ mg 2R = mgh =
1 mv 2
A
2
+ 2mv A2 = mhv A2 / R ⇒
2 = h / R ⇒ h = 5R / 2 = 10 m;
v A = 2g (h − 2R ) = 2 × 9.8 × (10 − 2 × 4) = 6.3 m / s;
v B = 2gh = 2 × 9.8 × 10 = 14 m / s.
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 22
Fine
Paolo Bagnaia - CTF - 1b - Esercizi di meccanica del punto e dei sistemi
♠ 23
Meccanica dei
fluidi
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
♠
1
Esercizi presi da Halliday-Resnick-Walker / Serway
notazione : “HRW capitolo [esercizi]” oppure “S capitolo [esercizi]”
! MECCANICA DEI FLUIDI :
HRW 15 [1E, 3E, 5P, 13E, 15E, 29E, 31E, 33E, 35E, 37P, 39P, 41P, 43P,
47E, 49P, 51E, 53E, 55P, 57P], S 15 [1, 5, 7, 9, 13, 15, 17, 21, 23, 25, 27, 31,
33, 35, 39, 45].
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
2
Esercizio – Un tubo ad “U” contiene due fluidi non miscibili : da un lato c’è
mercurio (massa volumica 13.6 g/cm3) fino all’altezza di 30 cm, dall’altro un
liquido ignoto, fino all’altezza di 100 cm. Calcolare la massa volumica di tale
liquido.
————————————
Soluzione –
h1ρ1g = h2ρ2g ⇒ ρ2 = h1ρ1/ h2 = 30 ×13.6 / 100 = 4.08 g/cm3.
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
♠
3
Esercizio – Quale frazione di un iceberg è sott’acqua ? (ρghiaccio=0.9 g/cm3)
————————————
Soluzione –
Dal principio di Archimede :
Vtotρgg = Vimmersoρag ⇒ Vimmerso / Vtotale= f = ρg/ ρa = 90%.
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
♠
4
Esercizio – Una lastra di ghiaccio (ρghiaccio=0.9 g/cm3) spessa 10 cm galleggia
su un fiume. Che superficie deve avere per impedire che un uomo di massa
50 Kg si bagni ?
————————————
Soluzione –
Dal principio di Archimede, nell’ipotesi che la lastra sia completamente
immersa :
Vρ g g + mg = Vρ a g = Sdρ g g + mg = Sdρ a g ⇒
S=
m
50
=
= 5m 2 .
d ( ρ a − ρ g ) 0.1× (1000 − 900 )
NB - attenzione !!! ρa = 1 g/cm3 (sistema CGS !!!).
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
♠
5
Esercizio – Un recipiente cilindrico di diametro 50 cm ha un buco sul fondo di
diametro 1 cm. Il recipiente è pieno d’acqua fino all’altezza di 20 cm. Trovare
la velocità di abbassamento del pelo dell’acqua.
————————————
Soluzione – Dalla legge di Bernoulli :
1 ρv 2
1
2
+ ρgh + p1 =
1 ρv 2
2
2
+ p2 ⇒
[p
2
2
p
Q
S
v
r
v
S
v
r
π
π
=
=
=
=
=
;
1
2
1 1
1 1
2 2
2 v2
v12
+ 2gh =
v1 =
2
 r12 
 v1 
 r2
 2 
r1
]
⇒
2gh
2 × 9 . 8 × 0. 2
=
= 0.079 cm / s.
4
4
( r1 / r2 ) − 1
(0.25 / 0.005 ) − 1
v1
h
r2
v2
NB - Il risultato è quasi uguale se si trascura il termine cinetico v12 nella legge
2
di Bernoulli : v1 = (r2 / r1) 2gh.
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
♠
6
Esercizio – Una mongolfiera piena di elio (ρe = 0.14 Kg/m3) ha forma sferica,
con raggio di 10 m. La strumentazione ha massa di 10 Kg. Nota la massa
volumica dell’aria (ρa = 1.3 Kg/m3), trovare la forza ascendente.
————————————
Soluzione –
Fasc = Vρag - Vρeg - Mg = 4/3 πR3 g (ρa - ρe) - Mg =
= 4/3 π × 103 × 9.8 × (1.3 - 0.14) - 10 × 9.8 = 4.76 × 104 N.
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
♠
7
Esercizio – Un corpo di massa 5 g e volume 11 cm3 è immerso in acqua,
trattenuto da una molla di costante elastica 6 × 10-3 N/cm. Calcolare
l’allungamento (o accorciamento) della molla.
————————————
Soluzione –
All’equilibrio (asse positivo verso l’alto) :
kd + V ρa g - mg = 0 ⇒
d = g (m - V ρa) / k = 980 × (5 - 11 × 1) / 600 = 9.8 cm.
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
♠
8
Esercizio – Una pompa di potenza 1 KW solleva acqua all’altezza di 5 m. In
quanto tempo svuota una pozza di 4 m3 ?
————————————
Soluzione –
L=Wt=Vρgh⇒
t = V ρ g h / W = 4 × 1000 × 9.8 × 5 / 1000 = 196 s = 3 min 16 s.
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
♠
9
Esercizio – Che potenza occorre per sollevare 50 litri d’acqua di un metro ed
immetterli in un condotto alla pressione di 2 atmosfere ?
————————————
Soluzione –
W = L / t = (mgh + V ∆p) / t = (.050 × 9.8 × 1 + .050 × 1 × 1.01 × 105) =
= 5050 W;
(in pratica il sollevamento è trascurabile rispetto alla compressione).
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
♠ 10
Fine
Paolo Bagnaia - CTF - 2 - Esercizi di Meccanica dei Fluidi
♠ 11
Termologia
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠
1
Esercizi presi da Halliday-Resnick-Walker / Serway
notazione : “HRW capitolo [esercizi]” oppure “S capitolo [esercizi]”
! CINEMATICA :
HRW 2 [1E, 3E, 9P, 11P, 13P, 19P, 29P, 33E, 35E, 37E, 39E, 41E, 43E, 47P,
49P, 51P, 55P, 57P, 61E, 63E, 65E, 67E, 71P, 77P, 79P, 83P, 85P, 89P],
HRW 3 [1E, 3E, 5P, 9E, 11E, 15P, 19E, 21E, 27P, 29P, 31P], HRW 4 [5E, 9E,
19E, 21E, 23E, 25E, 27E, 31E, 37P, 41P, 47P, 51E, 53E, 55E, 57E, 59E, 61P,
65P, 67E, 69E, 73E, 75P, 77P, 81P], S 1 [33, 35, 37, 39, 41, 49], S 2 [1,
7,9,11, 13, 17, 21, 23, 25, 29, 33, 35, 37, 43, 47], S 3 [3, 5, 7, 9, 11, 13, 15,
17, 19, 25, 27, 29, 31, 35, 37, 39, 41, 55].
! MECCANICA DEL PUNTO
HRW
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
2
Esercizio – Un cubetto di ghiaccio di 150 g alla temperatura di 0° C è gettato
in un recipiente, che contiene 300 g di acqua alla temperatura di 50° C. Dato il
calore latente di fusione del ghiaccio di 80 cal/g, trovare la temperatura finale.
————————————
Soluzione – Bilancio del calore assorbito e ceduto (m = mghiaccio; M = macqua):
Q ghiaccio = Qacqua = mλ + mc(Tfin - To) = Mc(Tini - Tfin) ⇒
Tfin = (McTini - mλ - mcTo) / (Mc + mc) = (300×1×50 - 150×80) / (300+150) =
= 6.6 °C.
NB - Abbiamo fatto l’esercizio con unità “pericolose” : calorie, gradi centigradi,
grammi; tutto bene, ma attenzione !
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠
3
Termodinamica
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠
4
Esercizio – Un recipiente di volume 820 cm3 contiene 2 g di O2 alla pressione
di 2 atm. Calcolare la temperatura.
————————————
Soluzione –
nmoli = 2 / 32 = 0.0625;
Dalla legge dei gas perfetti :
T = pV / (nR) = 2 × 1.01 × 105 × 820 × 10-6 / (0.0625 × 8.31) = 320 K = 47 °C.
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠
5
Esercizio – Un recipiente di volume 90 cm3 contiene 3.5 g di O2 alla
pressione di 28 atm. Calcolare la temperatura.
————————————
Soluzione –
nmoli = 3.5 / 32 = 0.109;
Dalla legge dei gas perfetti :
T = pV / (nR) = 28 × 1.01 × 105 × 90 × 10-6 / (0.109 × 8.31) = 281 K = 8 °C.
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠
6
Esercizio – Calcolare la velocità quadratica media dell’aria alla temperatura di
17 °C (supporre l’aria una mistura di peso molare effettivo 29 g/mole).
————————————
Soluzione –
Dalla teoria cinetica :
⟨v 2 ⟩ =
3nRT
3 × 8.31× ( 273 + 17)
=
= 500 m / s.
−3
M
29 × 10
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠
7
Esercizio – Trovare il rapporto tra la velocità quadratica media tra due
quantità di gas alla stessa temperatura, la prima di He, la seconda di N2.
————————————
Soluzione – Dalla teoria cinetica :
⟨v 2 ⟩ =
⟨v 2 ⟩
⟨v 2 ⟩
He
3nRT
⇒
M
=
mN2
mHe
=
28
= 2.65;
4
N2
La velocità quadratica media è maggiore per il gas He.
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠
8
Esercizio – Un recipiente sigillato di volume 4 litri contiene 5 g di N2 alla
temperatura di 20 °C. Se la temperatura viene portata a 40 °C, di quanto
aumenta la pressione ?
————————————
Soluzione –
nmoli = 5 / 28 = 0.178;
Dalla legge dei gas perfetti, a volume costante :
∆p = p2 - p1 = nRT2 / V - nRT1 / V = nR(T2 - T1) / V =
= 0.178 × 8.31 × (313 - 293) / .004 = 7396 N/m2 = 7396 Pa;
NB - Per calcolare la differenza di temperatura, non è necessario passare a K.
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠
9
Esercizio – Un gas compie un’espansione adiabatica, che raddoppia il
volume e diminuisce la temperatura di un fattore 1.32. Dire se si tratta di un
gas mono- oppure bi-atomico.
————————————
Soluzione – Dalla legge delle adiabatiche :
T1V1γ-1 = T2V2γ-1 ⇒ T1/T2 = (V2 / V1)γ-1 ⇒
γ = 1 + log(T1/T2) / log(V2 / V1) = 1 + log(1/1.32) / log(1/2) = 1.4 = 7/ 5 ⇒
biatomico.
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠ 10
Esercizio – Due quantità di gas, uno mono- e uno bi-atomico, hanno la stessa
temperatura e lo stesso volume. Subiscono entrambe una compressione
adiabatica, che ne dimezza il volume. Quale dei due gas è più caldo ?
————————————
Soluzione – Si applica la legge delle adiabatiche :
γ
γ
piniVini
= pfinVfin
γ
 2V
p
V 
= pfin  ini  ⇒ fin =  ini
pini  Vini
 2 
γ

 = 2γ ⇒

pfin Tfin Vini 2Tfin
Tfin
=
=
⇒
= 2γ −1 ⇒
pini Vfin Tini
Tini
Tini
Tfin;1 Tfin;1 Tini
2γ 1−1 2γ 1 25 / 3
=
= γ −1 = γ = 7 / 5 = 1.203;
Tfin;2 Tini Tfin;2 2 2
22 2
È più caldo il gas monoatomico.
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠ 11
Esercizio – Un gas si trova alla temperatura di 17 C, pressione di 2×105 Pa,
volume di 5 litri. Compie un’espansione isobara, il cui lavoro è 200 J. Trovare
la temperatura finale.
————————————
Soluzione –
L = p (Vfin - Vini) ⇒ Vfin = Vini + L / p ⇒ Vfin / Vini = 1 + L / (p Vini);
p Vini / Tini = p Vfin / Tfin ⇒
Tfin = Tini Vfin / Vini = Tini [1 + L / (p Vini)] =
= 290 × [1 + 200 / (2 × 105 × 5 × 10-3 )] = 348 K = 75 ºC.
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠ 12
Fine
Paolo Bagnaia - CTF - 3 - Esercizi di termologia e termodinamica
♠ 13
Elettrostatica
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
1
Esercizi presi da Halliday-Resnick-Walker / Serway
notazione : “HRW capitolo [esercizi]” oppure “S capitolo [esercizi]”
! CINEMATICA :
HRW 2 [1E, 3E, 9P, 11P, 13P, 19P, 29P, 33E, 35E, 37E, 39E, 41E, 43E, 47P,
49P, 51P, 55P, 57P, 61E, 63E, 65E, 67E, 71P, 77P, 79P, 83P, 85P, 89P],
HRW 3 [1E, 3E, 5P, 9E, 11E, 15P, 19E, 21E, 27P, 29P, 31P], HRW 4 [5E, 9E,
19E, 21E, 23E, 25E, 27E, 31E, 37P, 41P, 47P, 51E, 53E, 55E, 57E, 59E, 61P,
65P, 67E, 69E, 73E, 75P, 77P, 81P], S 1 [33, 35, 37, 39, 41, 49], S 2 [1,
7,9,11, 13, 17, 21, 23, 25, 29, 33, 35, 37, 43, 47], S 3 [3, 5, 7, 9, 11, 13, 15,
17, 19, 25, 27, 29, 31, 35, 37, 39, 41, 55].
! MECCANICA DEL PUNTO
HRW
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
2
Esercizio – Calcolare il campo elettrico nel punto centrale tra due cariche, di
valore q1=2×10-7 C e q2= -5×10-8 C, poste alla distanza di 10 cm.
————————————
Soluzione –
Dalla legge di Coulomb :
!
!
!
Etot = E1 + E2 =
q2 
1  q1
=
−
2
2

d
d
4πε 0  ( 2 ) ( 2 ) 
1
2 × 10 −7 + 5 × 10 −8
5
q
q
N / C.
9
.
04
10
(
)
=
×
=
−
=
1
2
−12
2
2
4 × π × 8.89 × 10 × (0.1)
πε 0d
nella direzione della carica negativa.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
3
Esercizio – Calcolare il campo elettrico nel punto centrale tra due cariche, di
valore q1=2×10-7 C e q2= +5×10-8 C, poste alla distanza di 10 cm (identico al
caso precedente, a parte il segno della seconda carica).
————————————
Soluzione –
Tutto identico al caso precedente, a parte i segni :
!
!
!
Etot = E1 + E2 =
q2 
1  q1
−
=
2
2


4πε 0  (d 2 ) (d 2 ) 
1
2 × 10 −7 − 5 × 10 −8
5
q
q
N / C.
(
)
5
.
4
10
=
−
=
=
×
1
2
−12
2
2
4 × π × 8.89 × 10 × (0.1)
πε 0d
nella direzione della carica minore (cioè q2).
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
4
Esercizio – Quattro cariche, ciascuna di valore 2 C, sono poste ai vertici di un
quadrato di lato 2 m. Calcolare il valore del campo elettrico al centro del
quadrato e al centro di ciascun lato.
————————————
Soluzione – Nel centro del quadrato, i campi si cancellano due a due e il
campo totale è nullo. Per quanto riguarda il campo nel punto centrale tra A e
B (gli altri tre casi sono analoghi), i campi delle cariche A e B si cancellano; i
campi delle cariche C e D hanno componente orizzontale che si cancella e
componente verticale che si somma. Essa vale :
A
B
2 Q
y
Etot
cos α =
= ECy + EDy = 2ECy =
2
4πε 0 d
L
Q
L
1
=
=
D
C
2
2
2
2
2πε 0 L + (L / 2) L + (L / 2)
=
1 Q
1
1
1
8 Q
=
= ???
2
2
2
2
2πε 0 L 1 + (1/ 2) 1 + (1/ 2)
2πε 0 5 5 L
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
5
Esercizio – Due cariche elettriche, di valore rispettivamente 1 C e -2 C, si
trovano alla distanza di 2 m. Trovare i punti in tutto lo spazio in cui il campo
elettrico totale è nullo.
————————————
Soluzione – Questi punti, se esistono, possono unicamente trovarsi sulla retta che
passa per i due punti. Infatti, nel resto dello spazio, i campi delle due cariche non sono
collineari, e pertanto la loro somma vettoriale non può essere nulla.
Sulla retta si possono inividuare tre zone : (a) tra infinito e prima carica, (b) tra le due
cariche, (c) tra seconda carica e infinito. In (b) i campi sono paralleli e pertanto la
somma non può essere nulla; in (c) il campo della seconda carica è sempre maggiore
(carica più grande a distanza minore); viceversa in (a) i due campi possono
compensarsi (q1 e q2 sono i moduli delle cariche) :
!
!
q2
q1
q2
1 q1
1
2
2
2
=
⇒
−
=
⇒
+
+
−
=0⇒
0
2
E1 = E2 =
q
x
q
L
q
xL
q
x
1
1
1
2
4πε0 x 2 4πε0 ( x + L)2
x 2 ( x + L)2
2
q ± q1 + q1(q2 − q1)
q ± q1q2 )
=L 1
= 2(1 ± 2 ) m → 4.8 m
x (q2 − q1) − 2q1xL − q1L = 0 ⇒ x = L 1
(q2 − q1)
(q2 − q1)
(a)
(b)
(c)
+
x
L
2
2
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
6
Esercizio – Come nel caso precedente, ma stavolta le cariche sono entrambe
positive (+1 C e +2 C).
————————————
Soluzione – Identica al caso precedente, ma stavolta la soluzione è nella zona (b) tra
le due cariche (q1 e q2 sono i moduli delle cariche) :
!
!
E1 = E2 =
1 q1
1
q2
q1
q2
=
⇒
−
=0⇒
2
2
4πε0 x 2 4πε0 (L − x )2
(L − x )
x
q1x 2 + q1L2 − 2q1xL − q2 x 2 = 0 ⇒ x 2 (q2 − q1) + 2q1xL − q1L2 = 0 ⇒
− q ± q1 + q1(q2 − q1)
− q ± q1q2 )
=L 1
=
x =L 1
(q2 − q1)
(q2 − q1)
2
= 2(−1 ± 2 ) m → 0.8 m
(a)
+
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
x
(b)
L
-
(c)
♠
7
Esercizio – Nel modello di Bohr dell’atomo di idrogeno, l’elettrone orbita
attorno al protone alla distanza di 0.5×10-8 cm. Trovare la forza di attrazione
elettrostatica tra le due particelle e la velocità dell’elettrone.
————————————
Soluzione –
Dalla legge di Coulomb :
1 e2
(1.6 × 10 −19 )2
−8
F=
N
9
.
26
10
=
=
×
−12
−10 2
2
4πε 0 r
4 × π × 8.89 × 10 × (0.5 × 10 )
Fr
mv 2
9.26 × 10 −8 × 0.5 × 10 −10
6
m / s.
F=
2
.
25
10
⇒v =
=
=
×
−31
m
r
9.11× 10
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
8
Esercizio – Due cariche, di valore q1=7×10-9 C e q2= 14×10-9 C sono poste
alla distanza di 40 cm. Trovare il lavoro necessario per avvicinarle alla
distanza di 25 cm.
————————————
Soluzione –
Dalla definizione di energia potenziale elettrostatica :
1 1
1
L=
q1q2  −  =
4πε 0
 r1 r2 
7 × 10 −9 × 14 × 10 −9  1
1 
−6
J.
1
.
3
10
=
−
=
×


−12
4 × π × 8.89 × 10  0.25 0.40 
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
9
Esercizio – Un elettrone (e=1.6×10-19 C, m=9.11×10-31 Kg) è scagliato alla
velocità di 106 m/s contro un secondo elettrone, che è mantenuto fermo.
Trovare la minima distanza cui arrivano i due elettroni.
————————————
Soluzione – La distanza minima corrisponde alla completa trasformazione
dell’energia cinetica in energia potenziale elettrostatica :
2
e
1
1 mv =
⇒
2
4πε 0 d
2
e2
2
2 × (1.6 × 10 −19 )2
−10
d=
m.
5
.
08
10
=
=
×
4πε 0 mv 2 4 × π × 8.89 × 10 −12 × 9.11× 10 −31 × (10 −6 )2
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠ 10
Esercizio – Un condensatore piano ha un campo di 104 V/m e una lunghezza
(parallela alle armature) di 5 cm. Un elettrone entra tra le armature con una
velocità di 107 m/s ortogonale al campo. Calcolare l’angolo di deflessione
all’uscita del condensatore e il modulo della velocità. Trascurare gli effetti di
bordo.
————————————
Soluzione – La forza elettrostatica (lungo l’asse y) è ortogonale alla velocità
iniziale dell’elettrone (asse x). Pertanto :
α v
fin
x = v 0 x t ⇒ t = x / v 0 x ⇒ Ttot = L / v 0 x ; v y = at ⇒
v y ,fin
Ee L
10 4 × 1.6 × 10 −19 × .05
6
m / s;
8
.
8
10
=
×
=
=
−
31
7
m v0 x
9.11× 10 × 10
 v y ,fin 
8.8 × 106
"
41
3;
 = a tan
=
α = a tan
7
10
 v0x 
2
E
L
vo
m
2
v tot ,fin = v y ,fin + v 0 x = (8.8 × 106 )2 + (107 )2 = 1.33 × 107 m / s.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠ 11
Fine
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠ 12
Correnti
continue
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
1
Esercizi presi da Halliday-Resnick-Walker / Serway
notazione : “HRW capitolo [esercizi]” oppure “S capitolo [esercizi]”
! CINEMATICA :
HRW 2 [1E, 3E, 9P, 11P, 13P, 19P, 29P, 33E, 35E, 37E, 39E, 41E, 43E, 47P,
49P, 51P, 55P, 57P, 61E, 63E, 65E, 67E, 71P, 77P, 79P, 83P, 85P, 89P],
HRW 3 [1E, 3E, 5P, 9E, 11E, 15P, 19E, 21E, 27P, 29P, 31P], HRW 4 [5E, 9E,
19E, 21E, 23E, 25E, 27E, 31E, 37P, 41P, 47P, 51E, 53E, 55E, 57E, 59E, 61P,
65P, 67E, 69E, 73E, 75P, 77P, 81P], S 1 [33, 35, 37, 39, 41, 49], S 2 [1,
7,9,11, 13, 17, 21, 23, 25, 29, 33, 35, 37, 43, 47], S 3 [3, 5, 7, 9, 11, 13, 15,
17, 19, 25, 27, 29, 31, 35, 37, 39, 41, 55].
! MECCANICA DEL PUNTO
HRW
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
2
Esercizio – Un conduttore di rame (peso atomico 63.5 g/mole, massa
volumica 8.9 g/cm3) ha una sezione costante di 1.3 cm2 ed è percorso dalla
corrente di 2 A. Calcolare la velocità media degli elettroni.
————————————
Soluzione –
Nmoli/m3 : Mrame/(Vmmole) = ρ / mmole = 8.9×103×1/(63.5×10-3) =1.4×105 moli/m3;
Nelettroni di conduzione / mole
: NAvogadro = 6.02×1023 ;
Nelettroni / m3 : NAvogadro × ρV / mmole = 6.02×1023 ×1.4×105 = 8.44×1028 m-3;
i=nSev ⇒ v = i / (nSe) = 2 / (8.44×1028×1.3×10-4×1.6×10-19) = 1.14×10-6 m/s.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
3
Esercizio – Una stufa è alimentata da una d.d.p. di 240 V con una corrente da
10 A. Determinare la resistenza della stufa e la potenza dissipata.
————————————
Soluzione –
V = R i ⇒ R = V / i = 240 / 10 = 24 Ω;
W = V i = 240 × 10 = 2400 W
cioè, a parità di i, ddp → 2 ddp ⇒ R → 2 R, W → 2 W.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
4
Esercizio – Una stufa è alimentata da una d.d.p. di 120 V con una corrente da
20 A. Determinare la resistenza della stufa e la potenza dissipata.
————————————
Soluzione –
V = R i ⇒ R = V / i = 120 / 20 = 6 Ω;
W = V i = 120 × 20 = 2400 W
cioè, a parità di d.d.p., i → 2i ⇒ R → R / 2, W → 2 W.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
5
Esercizio – Una stufa è alimentata da una d.d.p. di 120 V con una corrente da
10 A. Determinare la resistenza della stufa e la potenza dissipata.
————————————
Soluzione –
V = R i ⇒ R = V / i = 120 / 10 = 12 Ω;
W = V i = 120 × 10 = 1200 W.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
6
Esercizio –
Circuito :
R1 = 4 Ω; R2 = 2 Ω;
R3 = 4 Ω; i1 = 3 A;
trovare i2, i3, ∆VAB.
R1
A
R2
B
R3
————————————
Soluzione –
Rtot = R1 + R2 R3 / (R2 + R3) = 4 + 2×4 / (2 + 4) = 16/3 Ω = 5.33 Ω;
∆Vtot = Rtot i1 = 5.33×3 = 16 V;
V2 = ∆Vtot - R1 i1 = 16 - 4×3 = 4 V ⇒ i2 = V2 / R2 = 4 / 2 = 2 A;
V3 = V2 = 4 V ⇒ i3 = V3 / R3 = 4 / 4 = 1 A.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
7
Esercizio – Circuito :
R1 = R2 = R6 = 4 Ω;
R3 = 8 Ω;
R4 = R5 = 2 Ω;
∆V = 24V;
trovare W6, Rtot.
R1
∆V
R4
R3
R2
R6
R5
————————————
Soluzione –
Rtot = R1 + R2 +
8×8
R3 (R4 + R5 + R6 )
= 4+4+
= 12 Ω;
16
R 3 + R 4 + R5 + R 6
i tot = ∆V / Rtot = 24 / 12 = 2 A;
 i 3 + i 6 = 2;
 i 3 + i 6 = 2;
⇒ 
⇒ i 3 = i 6 = 1 A;

8i 3 − 8i 6 = 0;
R3i 3 = (R4 + R5 + R6 )i 6 ;
W6 = i 62R6 = 4 W .
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
8
Esercizio – Circuito (ponte di Wheatstone) :
R1 = 30 Ω; R2 = 45 Ω; R3 = 200 Ω;
∆V = 2V; ig = 0 (ruotare il potenziometro);
trovare R4, i1, i2, i3, i4.
R1
————————————
Soluzione –
∆V1 = ∆V3 ⇒ ∆V1 = R1i1 = ∆V3 = R3i 3 ;
R2
g
R3
analogamente R2i 2 = R4i 4 ;
poiche' i g = 0 ⇒ i1 = i 2 ; i 3 = i 4 ;
R4
∆V
R1i1 = R3i 3 ; R2i1 = R 4i 2 ⇒ (R1 + R2 )i1 = ∆V1 + ∆V2 = ∆V ;
i1 = i 2 = ∆V /(R1 + R2 ) = 2 / 75 = 27 mA; ∆V1 = R1i1 = 30 × 0.027 = 0.8 V ;
∆V2 = R2i 2 = 45 × 0.027 = 1.2 V ; i 3 = i 4 = ∆V1 / R3 = 0.8 / 200 = 4 mA;
R 4 = ∆V2 / i 4 = 1.2 / 0.004 = 300 Ω.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠
9
Esercizio – Un fornello elettrico di potenza 500 W porta un litro di acqua dalla
temperatura ambiente di 16 °C all’ebollizione in 20 minuti. Calcolare la
frazione di calore dispersa nell’ambiente.
————————————
Soluzione –
Qtot = W t = 500 × 20 × 60 = 6×105 J = 1.435×105 cal;
Qacqua = mc(Tfin - Tini) = 1 × 103×(100 – 16) = 8.4×104 cal;
η = (Qtot - Qacqua) / Qtot = 1 – 8.4×104 / (1.435×105) = 41.5 %.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠ 10
Esercizio – Una teiera elettrica può essere riscaldata con due resistenze
elettriche. Utilizzando la prima si prepara il tè in 15 minuti, mentre con la
seconda occorrono 30 minuti. Trascurando la dispersione di calore
nell’ambiente, calcolare il tempo necessario per fare il tè utilizzando le due
reistenze in serie oppure in parallelo.
————————————
Soluzione –
1° caso : W1 = ∆V2 / R1 ; Q = W1 t1 = ∆V2 t1 / R1 ;
2° caso : W2 = ∆V2 / R2 ; Q = W2 t2 = ∆V2 t2 / R2 ; [Q e ∆V sono gli stessi !!!]
rapporto : t1 / t2 = R1 / R2 = ½ ⇒ R1 = ½ R2 ;
a) serie : Rtot;a = R1+R2 = 1.5 R2 ⇒ ta/ t2 = Rtot;a / R2 ⇒ ta = t2Rtot;a / R2 = 45 min.
b) parallelo : Rtot;b = R1R2 /(R1+R2) = R2/3 ⇒ tb = t2Rtot;b / R2 = 10 min.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠ 11
Campo
magnetico
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠ 12
Esercizio – Due conduttori rettilinei, in cui passa una corrente di 2 A e 3 A
rispettivamente, formano una croce, sfiorandosi senza toccarsi. Calcolare il
valore del campo magnetico nei quattro punti posti a 2 cm da entrambi i
conduttori.
————————————
Soluzione – I campi sono tutti ortogonali al
piano; chiamiamo “+” il verso uscente :
A)
z
Btot
=
B1z
− B2z
µ 0  i1 i 2 
µ0
(i1 − i 2 ) =
=
 − =
2π  L L  2π L
i2
D
2 × 10 −7
=
× (2 − 3) = −1× 10 −5 T ;
0.02
B)
z
Btot
C)
z
Btot
−5
=
−B1z
− B2z
= −5 × 10
=
−B1z
+ B2z
−5
= 1× 10
T;
L
A
L
i1
C
B
T;
z
D) Btot
= B1z + B2z = 5 × 10 −5 T ;
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠ 13
Esercizio – Una bobina rettangolare, di lati 5 cm e 3 cm, composta da 100
spire, ruota compiendo 10 giri al secondo all’interno di un campo magnetico di
2 T, ortogonale all’asse di rotazione della spira. Calcolare la f.e.m. indotta.
————————————
Soluzione – Calcoliamo il flusso del campo attraverso la spira, in funzione del
tempo, poi deriviamo :
! !
Φ B = NB ⋅ S = NBab sin(ωt ) = NBab sin(2πν t );
ℑ=
dΦ B d
= [NBab sin( 2πν t )] = 2πνNBab cos(2πν t );
dt
dt
ℑmax = 2 × π × 10 × 100 × 2 × 0.05 × 0.03 = 18.8 V ;
ω = 2πν = 2 × π × 10 = 62.8 s −1.
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠ 14
Esercizio – Una bobina quadrata, di lato 20 cm, ha un lato che è libero di
scorrere rispetto agli altri. La bobina è fatta di materiale conduttore con
resistenza 2 Ω, indipendente dalla posizione del lato mobile. La bobina si
trova in un campo magnetico di 3 T, ortogonale ad essa, con il lato mobile che
si muove alla velocità di 4 m/s verso l’esterno. Calcolare la corrente indotta.
————————————
Soluzione – Calcoliamo il flusso in funzione del tempo, poi deriviamo :
! !
Φ B = B ⋅ S = Ba(a + vt );
i=
1 dΦ B 1 d
[Ba(a + vt )] = Bav = 3 × 0.2 × 4 = 1.2 A.
=
2
R
R dt
R dt
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠ 15
Fine
Paolo Bagnaia - CTF - 4 - Esercizi di elettrostatica e correnti
♠ 16
Ottica
Paolo Bagnaia - CTF - 1x - Esercizi di yy
♠
1
Esercizi presi da Halliday-Resnick-Walker / Serway
notazione : “HRW capitolo [esercizi]” oppure “S capitolo [esercizi]”
! CINEMATICA :
HRW 2 [1E, 3E, 9P, 11P, 13P, 19P, 29P, 33E, 35E, 37E, 39E, 41E, 43E, 47P,
49P, 51P, 55P, 57P, 61E, 63E, 65E, 67E, 71P, 77P, 79P, 83P, 85P, 89P],
HRW 3 [1E, 3E, 5P, 9E, 11E, 15P, 19E, 21E, 27P, 29P, 31P], HRW 4 [5E, 9E,
19E, 21E, 23E, 25E, 27E, 31E, 37P, 41P, 47P, 51E, 53E, 55E, 57E, 59E, 61P,
65P, 67E, 69E, 73E, 75P, 77P, 81P], S 1 [33, 35, 37, 39, 41, 49], S 2 [1,
7,9,11, 13, 17, 21, 23, 25, 29, 33, 35, 37, 43, 47], S 3 [3, 5, 7, 9, 11, 13, 15,
17, 19, 25, 27, 29, 31, 35, 37, 39, 41, 55].
! MECCANICA DEL PUNTO
HRW
Paolo Bagnaia - CTF - 1x - Esercizi di yy
2
Esercizio – In quale direzione un subacqueo vede il sole che tramonta ?
(nacqua = 1.33)
————————————
Soluzione –
L’effetto è causato dal cambio di direzione della luce che entra nell’acqua.
Dalla legge di Snell :
sin i / sin r = nr / ni ⇒
sin 90° / sin α = nacqua / naria ⇒
α
sin α = 1 / 1.33 = 0.752 ⇒
α = 48° 75.
Paolo Bagnaia - CTF - 1x - Esercizi di yy
♠
3
Acustica
Paolo Bagnaia - CTF - 1x - Esercizi di yy
♠
4
Esercizio – Un aeroplano emette suoni con la potenza di 5 W. Quale è
l’intensità sonora a 1 m, 10 m, 1 Km ? Se la soglia auditiva è a 50 dB, a che
distanza è udibile ?
————————————
Soluzione – Dalla definizione di intensità sonora :
β = 10 Log10 I/I0 = 10 Log10 [W/(4πR2 I0)]
[I0 = 10-12 W/m2];
a) β1(1 m) = 10 Log10 [W/(4πR2 I0)] = 10 Log10 [5 / (4×π×12×10-12)] = 116 dB;
b) β2(10 m) = 10 Log10 [5 / (4×π×102×10-12)] = 96 dB;
c) β3(1 Km) = 10 Log10 [5 / (4×π×10002×10-12)] = 56 dB;
d) β4 = 10 Log10 [W/(4πx2 I0)] ⇒
x = [W / (4π I0 10β/10)]½ = [5 / (4×π×10-12×105)]½ = 1995 m = 1.99 Km.
Paolo Bagnaia - CTF - 1x - Esercizi di yy
♠
5
Fine
Paolo Bagnaia - CTF - 1x - Esercizi di yy
♠
6