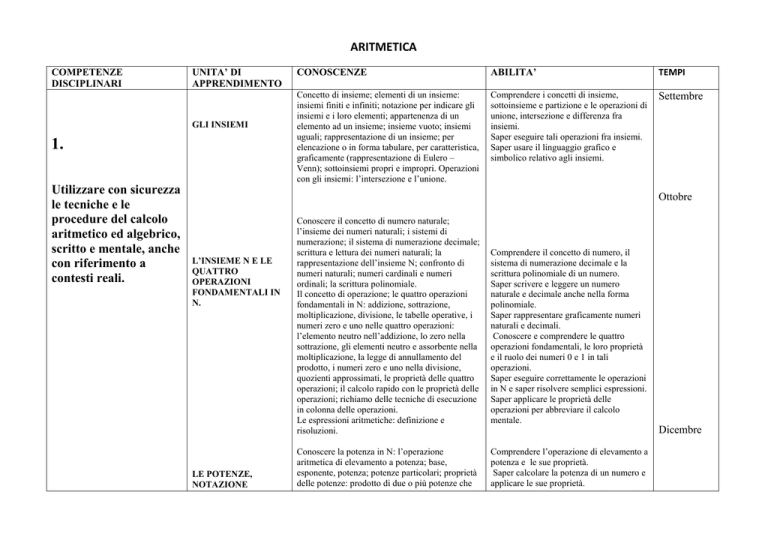
ARITMETICA
COMPETENZE
DISCIPLINARI
UNITA’ DI
APPRENDIMENTO
GLI INSIEMI
1.
Utilizzare con sicurezza
le tecniche e le
procedure del calcolo
aritmetico ed algebrico,
scritto e mentale, anche
con riferimento a
contesti reali.
CONOSCENZE
ABILITA’
TEMPI
Concetto di insieme; elementi di un insieme:
insiemi finiti e infiniti; notazione per indicare gli
insiemi e i loro elementi; appartenenza di un
elemento ad un insieme; insieme vuoto; insiemi
uguali; rappresentazione di un insieme; per
elencazione o in forma tabulare, per caratteristica,
graficamente (rappresentazione di Eulero –
Venn); sottoinsiemi propri e impropri. Operazioni
con gli insiemi: l’intersezione e l’unione.
Comprendere i concetti di insieme,
sottoinsieme e partizione e le operazioni di
unione, intersezione e differenza fra
insiemi.
Saper eseguire tali operazioni fra insiemi.
Saper usare il linguaggio grafico e
simbolico relativo agli insiemi.
Settembre
Ottobre
L’INSIEME N E LE
QUATTRO
OPERAZIONI
FONDAMENTALI IN
N.
LE POTENZE,
NOTAZIONE
SCIENTIFICA E
Conoscere il concetto di numero naturale;
l’insieme dei numeri naturali; i sistemi di
numerazione; il sistema di numerazione decimale;
scrittura e lettura dei numeri naturali; la
rappresentazione dell’insieme N; confronto di
numeri naturali; numeri cardinali e numeri
ordinali; la scrittura polinomiale.
Il concetto di operazione; le quattro operazioni
fondamentali in N: addizione, sottrazione,
moltiplicazione, divisione, le tabelle operative, i
numeri zero e uno nelle quattro operazioni:
l’elemento neutro nell’addizione, lo zero nella
sottrazione, gli elementi neutro e assorbente nella
moltiplicazione, la legge di annullamento del
prodotto, i numeri zero e uno nella divisione,
quozienti approssimati, le proprietà delle quattro
operazioni; il calcolo rapido con le proprietà delle
operazioni; richiamo delle tecniche di esecuzione
in colonna delle operazioni.
Le espressioni aritmetiche: definizione e
risoluzioni.
Conoscere la potenza in N: l’operazione
aritmetica di elevamento a potenza; base,
esponente, potenza; potenze particolari; proprietà
delle potenze: prodotto di due o più potenze che
hanno la stessa base, quoziente di due potenze che
Comprendere il concetto di numero, il
sistema di numerazione decimale e la
scrittura polinomiale di un numero.
Saper scrivere e leggere un numero
naturale e decimale anche nella forma
polinomiale.
Saper rappresentare graficamente numeri
naturali e decimali.
Conoscere e comprendere le quattro
operazioni fondamentali, le loro proprietà
e il ruolo dei numeri 0 e 1 in tali
operazioni.
Saper eseguire correttamente le operazioni
in N e saper risolvere semplici espressioni.
Saper applicare le proprietà delle
operazioni per abbreviare il calcolo
mentale.
Dicembre
Comprendere l’operazione di elevamento a
potenza e le sue proprietà.
Saper calcolare la potenza di un numero e
applicare le sue proprietà.
Saper scrivere un numero con la notazione
SCIENTIFICA E
ORDINE DI
GRANDEZZA
DIVISIBILITA’,M.C.D.
ed m.c.m.
FRAZIONI
hanno la stessa base, quoziente di due potenze che
hanno la stessa base, potenza di una potenza,
prodotto di due o più potenze aventi lo stesso
esponente, quoziente di due potenze che hanno lo
stesso esponente; proprietà distributiva
dell’elevamento a potenza rispetto alla
moltiplicazione e alla divisione; calcolo rapido;
uso delle tavole numeriche; espressioni
numeriche con potenze.
Saper scrivere un numero con la notazione
esponenziale e in forma standard e saper
individuare l’ordine di grandezza di un
numero.
Conoscere : divisibilità; multipli e divisori di un
numero naturale; criteri di divisibilità; numeri
primi e numeri composti; la
fattorizzazione , scomposizione di un numero in
fattori primi; applicazioni della fattorizzazione;
Massimo Comun Divisore e minimo comune
multiplo: M.C.D., rappresentazione grafica del
M.C.D., metodo insiemistico e metodo della
fattorizzazione per calcolare il M.C.D.; numeri
primi tra loro; m.c.m., rappresentazione grafica
del m.c.m., metodo insiemistico e della
fattorizzazione per calcolare il m.c.m..
Comprendere i concetti di divisibilità,
multiplo, sottomultiplo, numero primo,
M.C.D. e m.c.m. di due o più numeri e le
loro proprietà.
Saper individuare i divisori e i multipli di
un numero.
Saper scomporre in fattori primi un
numero.
Saper calcolare il M.C.D. e m.c.m. di due
o più numeri.
Saper usare il linguaggio grafico di
rappresentazione del M.C.D. e m.c.m..
Conoscere l’unità frazionaria; la frazione come
operatore; la frazione come quoziente esatto fra
numeri naturali; l’insieme dei numeri naturali;
frazioni proprie e frazioni improprie, frazioni
apparenti; frazioni equivalenti e classi di
equivalenza; proprietà invariantiva delle frazioni;
Comprendere i concetti di unità frazionaria
e frazione.
Saper riconoscere frazioni proprie,
improprie e apparenti, frazioni
complementari e frazioni
equivalenti.
Saper ridurre una frazione ai minimi
Gennaio
Marzo
Maggio
applicazioni del concetto di equivalenza: frazioni
riducibili e irriducibili, semplificazione di una
frazione, riduzione di una frazione ai minimi
termini; trasformazione di una frazione in un’altra
equivalente di denominatore dato; riduzione di
più frazioni al minimo comun denominatore;
confronto di frazioni.
NUMERI
RAZIONALI
4.
Riconoscere e risolvere
problemi di vario
genere, individuando le
strategie appropriate,
giustificando il
procedimento seguito e
utilizzando in modo
consapevole i linguaggi
specifici
Conoscere le operazioni nell’insieme Q+;
addizione; sottrazione; numeri misti; frazioni
complementari; moltiplicazione; semplificazione
nella moltiplicazione; frazioni inverse o
reciproche, divisione; potenza; espressioni con le
frazioni. Problemi con le frazioni: calcolo del
valore della frazione di un numero dato; calcolo
di un numero di cui si conosce il valore di una sua
frazione; calcolo di due numeri di cui è noto che
uno è una data frazione dell’altro e di cui si
conosce la somma e la differenza.
termini, ridurre più frazioni al m.c.d. e
confrontare due o più frazioni.
Saper rappresentare una frazione come
operatore su un intero.
Comprendere il concetto di numero
razionale.
Consapevolezza e padronanza di calcolo
con i numeri razionali.
Saper risolvere problemi con le frazioni.
Saper rappresentare i numeri razionali e
l’insieme Q+.
Aprile
Maggio
PROBLEMI
Problemi: generalità; fasi risolutive di un
problema; tecniche risolutive di un problema:
metodo grafico; ricorso alle espressioni
aritmetiche e diagrammi di flusso.
Saper risolvere semplici problemi già
strutturati.
Saper comprendere il significato del testo
di un problema.
Saper riconoscere i dati indispensabili, i
dati superflui e quelli mancanti.
Saper individuare le incognite.
Saper applicare il metodo opportuno per
risolvere i problemi.
Saper trovare e verificare la soluzione di
un problema.
GEOMETRIA
COMPETENZE
DISCIPLINARI
2.
Rappresentare,
confrontare ed
analizzare figure
geometriche,
individuandone
varianti, invarianti,
relazioni, soprattutto
apartire da situazioni
reali
UNITA’ DI
APPRENDIMENTO
ENTI GEOMETRICI
FONDAMENTALI
ANGOLI
RETTE
IL SISTEMA METRICO
DECIMALE E NON
DECIMALE
CONOSCENZE
ABILITA’
TEMPI
Punto, linea, retta, superficie, piano, semipiano;
gli assiomi degli enti geometrici fondamentali; il
rapporto tra gli enti geometrici fondamentali; la
semiretta e il segmento; segmenti consecutivi e
adiacenti, confronto di due segmenti; punto medio
di un segmento, operazioni con i segmenti:
addizione e sottrazione di segmenti, multipli e
sottomultipli di un segmento; distanza fra due
punti; spezzate.
Saper applicare i concetti studiati e le loro
proprietà.
Saper rappresentare gli enti geometrici
studiati ed eseguire semplici costruzioni
geometriche con l’uso di opportuni
strumenti.
Novembre
Angoli come sottoinsiemi del piano: angoli
convessi e angoli concavi; i rapporti tra gli angoli:
angoli consecutivi; adiacenti, opposti al vertice;
confronto fra due angoli; operazioni con gli
angoli: addizione di angoli; sottrazione fra due
angoli; multipli e sottomultipli di un angolo;
bisettrice di un angolo; l’angolo retto; angoli acuti
e angoli ottusi; angoli complementari, angoli
supplementari, angoli esplementari.
Saper classificare gli angoli;
Saper risolvere problemi in cui sia data la
somma o la differenza di angoli;
Eseguire le quattro operazioni con misure
angolari;
Risolvere problemi relativi agli angoli;
Confronto tra angoli.
Posizione reciproca di due rette nel piano; rette
perpendicolari; perpendicolare per un punto ad
una retta data; distanza di un punto da una retta;
proiezione di un punto e di un segmento su una
retta; asse di un segmento; rette parallele;
parallele ad una retta data passante per un punto
non appartenente ad essa; fascio di rette parallele,
angoli formati da due rette e una trasversale;
angoli formati da due rette parallele tagliate da
una trasversale; criteri di parallelismo;
applicazioni del parallelismo: distanza fra due
rette parallele.
Comprendere il significato di parallelismo
e perpendicolarità;
Saper individuare relazioni tra gli angoli
formati tra due rette parallele tagliate da
una trasversale;
Saper individuare la relazione tra rette;
Saper individuare rette parallele e
perpendicolari.
Concetto di grandezza; grandezze omogenee;
misura di una grandezza; l’unità di misura; il
sistema di misura decimale; il sistema
internazionale di misura; misure di lunghezza, di
superficie, di volume, di capacità, di peso; sistemi
Comprendere i concetti di grandezza e sua
misura, i sistemi di misura del S.I.
decimali e non, i concetti di peso e di peso
specifico e loro relazioni.
Saper operare nei vari sistemi di misura
studiati.
Dicembre
Gennaio
Febbraio
superficie, di volume, di capacità, di peso; sistemi
di misura degli angoli: ampiezza di un angolo,
sistema sessagesimale; le espressioni complesse;
forma normale di una espressione complessa;
operazioni sulle espressioni complesse; problemi
sulle misure.
I POLIGONI
I TRIANGOLI
Saper risolvere problemi riguardanti la
misura delle grandezze.
Conoscere e saper usare il linguaggio
matematico relativo agli argomenti
studiati.
Figure geometriche del piano: i poligoni:
generalità, elementi di un poligono; il perimetro;
poligoni convessi e concavi; angoli esterni ed
interni; denominazione dei poligoni; diagonali di
un poligono; poligoni equilateri, equiangoli,
regolari; relazione fra i lati di un poligono;
relazione fra gli angoli di un poligono.
Comprendere le proprietà, le
caratteristiche e la classificazione dei
poligoni ed esporle con linguaggio
rigoroso.
Saper riconoscere le figure congruenti e
isoperimetriche.
Saper calcolare le ampiezze di angoli
interni ed esterni.
Triangoli: generalità; elementi dei triangoli;
classificazione dei triangoli rispetto ai lati;
classificazione dei triangoli rispetto agli angoli; il
triangolo rettangolo; gli angoli interni dei
triangoli
particolari
(rettangoli,
isoscele,
equilatero); linee particolari e punti notevoli del
triangolo: le tre altezze e l’ortocentro, le tre
mediane e il baricentro, le tre bisettrici e
l’incentro, i tre assi e il circocentro; proprietà
particolari di alcuni tipi di triangolo: isoscele,
equilatero, rettangolo.
Comprendere le proprietà, le
caratteristiche e la classificazione dei
triangoli ed esporle con linguaggio
rigoroso
Classificare i triangoli (costruzione di
opportuni diagrammi di Venn).
Risolvere problemi sul perimetro anche
con frazioni, ricorrendo a modelli
opportuni.
Usare con sicurezza le opportune unità di
misura.
Marzo
Aprile
Maggio
I QUADRILATERI
Quadrilateri:
generalità;
proprietà
dei
quadrilateri; gli elementi costitutivi di un
quadrilatero ;classificazione dei quadrilateri
rispetto ai lati; classificazione dei quadrilateri
rispetto agli angoli; (trapezi, parallelogrammi
,rettangoli, rombi e quadrati).
Conoscere le proprietà geometriche dei
quadrilateri ed esporle con linguaggio
rigoroso.
Classificare i quadrilateri (costruzione di
opportuni diagrammi di Venn).
Risolvere problemi sul perimetro anche
con frazioni, ricorrendo a modelli
opportuni.
Usare con sicurezza le opportune unità di
misura.
SCIENZE
COMPETENZE
DISCIPLINARI
1.
Osservare, analizzare e
descrivere fenomeni
appartenenti alla realtà
naturale e agli aspetti
della vita quotidiana,
formulare e verificare
ipotesi, utilizzando
semplici
schematizzazioni e
modellizzazioni.
UNITA’ DI
APPRENDIMENTO
IL METODO
SPERIMENTALE
CONOSCENZE
ABILITA’
TEMPI
Le fasi del metodo sperimentale,
applicare il metodo scientifico; misura
di una grandezza; l’unità di misura; il
sistema di misura decimale; il sistema
internazionale di misura; misure di
lunghezza, di superficie, di volume, di
capacità, di peso; analisi dei dati;
rappresentazione dei dati.
Saper applicare le fasi del metodo
sperimentale.
Saper fare misurazioni di lunghezza ,volume,
massa, densità.
Saper utilizzare i più diffusi strumenti di
misura: riga, bilancia, recipienti graduati,
cronometro.
Sapere come si analizzano e si rappresentano i
dati.
Ottobre
Rilevare e descrivere le proprietà
caratteristiche della materia , delle sostanze e
dei corpi;
Distinguere gli stati di aggregazione della
materia;
Individuare proprietà caratteristiche e
differenze dei tre stati di aggregazione.
Novembre
LA MATERIA E I SUOI
STATI DI
Conoscere il significato di materia,
AGGREGAZIONE
sostanza e corpo;
Conoscere la differenza dei concetti di
massa, peso, densità e peso specifico;
Conoscere gli stati di aggregazione della
materia e le loro caratteristiche.
IL CALORE E LA
TEMPERATURA
Conoscere il significato di calore e
temperatura e i loro sistemi di
misurazione. Conoscere i cambiamenti
di stato e le loro caratteristiche.
Conoscere il fenomeno della dilatazione
termica. Conoscere il concetto di calore
specifico. Conoscere le modalità di
propagazione del calore.
Conoscere il concetto di equilibrio
termico.
Riconoscere la diversità tra calore e
temperatura;
Osservare e descrivere i passaggi di stato.
Individuare fenomeni di dilatazione termica
nella realtà;
Individuare le modalità di propagazione del
calore;
Distinguere conduttori e isolanti termici.
Gennaio
Febbraio
2.
Utilizza il proprio
patrimonio di conoscenze L’ORGANIZZAZIONE
per comprendere le
DEI VIVENTI.
problematiche scientifiche
di attualità e per assumere
comportamenti
responsabili in relazione
al proprio stile di vita, alla
promozione della salute
ed all’uso delle risorse.
Conoscere le caratteristiche dei viventi :
il ciclo vitale e l’organizzazione
cellulare;
Conoscere la struttura e i componenti di
una cellula animale e vegetale;
Riconoscere le caratteristiche della “ vita”;
Riconoscere la struttura e i componenti di una
cellula individuandone le funzioni;
Distinguere la cellula animale e quella
vegetale, la cellula eucariote e quella
procariote;
Distinguere riproduzione sessuata e asessuata.
Marzo
Conoscere la riproduzione cellulare;
Conoscere la specializzazione e
l’organizzazione delle cellule;
Maggio
Conoscere la riproduzione dei viventi.
3.
Riconoscere le principali
interazioni tra mondo
biotico ed abiotico,
individuandone la
problematicità
dell’intervento antropico
negli ecosistemi
IL SUOLO
Conoscere il significato di suolo e le sue
caratteristiche.
Conoscere la composizione del suolo e i
vari tipi di suolo.
Conoscere come le caratteristiche del
suolo influenzano la vita delle piante.
Riconoscere i vari tipi di suolo, mediante le
loro caratteristiche fisico e chimiche.
Descrivere il profilo del suolo.
Individuare le diversità tra suolo naturale e
suolo agricolo.
Mettere in relazione composizione e struttura
del suolo con i suoi abitanti.
Dicembre
Gennaio









