Parallelogrammi e teorema di Talete

L2.mat, punto di formazione per Matematica e Fisica
Parallelogrammi e teorema di Talete
Problema
Si consideri il parallelogramma ABCD e sano E ed F i punti medi rispettivamente dei lati AB, CD.
Congiungere A con F e C con E; tracciare la diagonale BD. Siano G ed H rispettivamente i punti di
intersezione di AF e CE con BD.
1. Dimostrare che i segmenti DG, GH, HB sono congruenti.
2. Dimostrare che EF taglia GH nel suo punto medio.
Dimostrazione
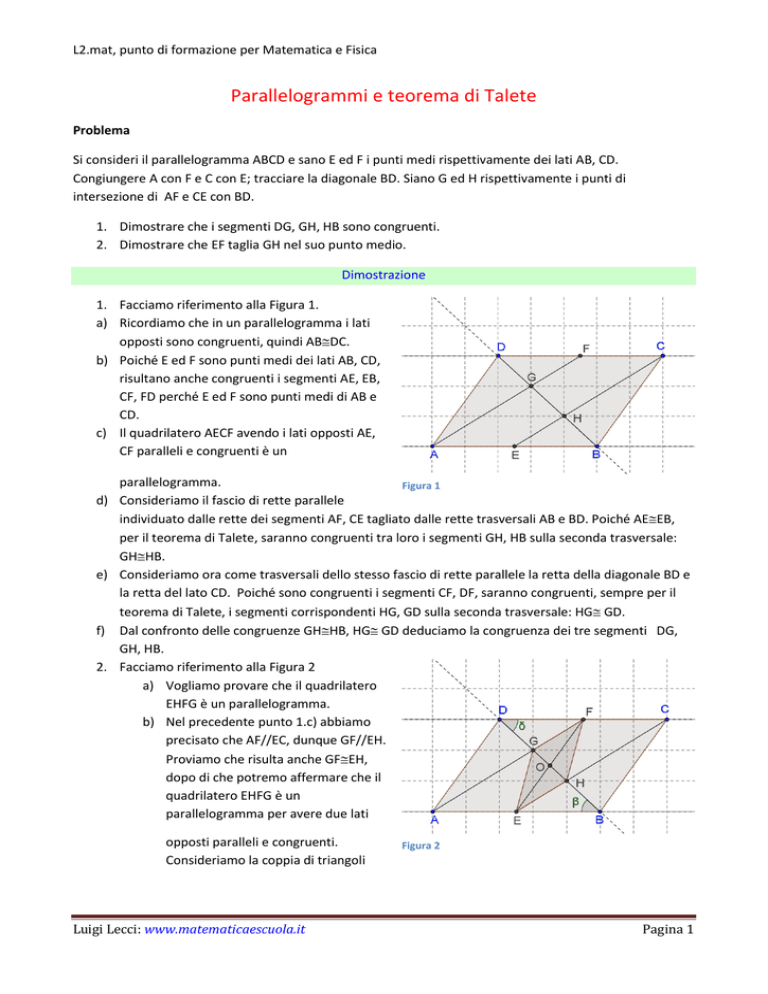
1. Facciamo riferimento alla Figura 1.
a) Ricordiamo che in un parallelogramma i lati
opposti sono congruenti, quindi ABDC.
b) Poiché E ed F sono punti medi dei lati AB, CD,
risultano anche congruenti i segmenti AE, EB,
CF, FD perché E ed F sono punti medi di AB e
CD.
c) Il quadrilatero AECF avendo i lati opposti AE,
CF paralleli e congruenti è un
parallelogramma.
Figura 1
d) Consideriamo il fascio di rette parallele
individuato dalle rette dei segmenti AF, CE tagliato dalle rette trasversali AB e BD. Poiché AEEB,
per il teorema di Talete, saranno congruenti tra loro i segmenti GH, HB sulla seconda trasversale:
GHHB.
e) Consideriamo ora come trasversali dello stesso fascio di rette parallele la retta della diagonale BD e
la retta del lato CD. Poiché sono congruenti i segmenti CF, DF, saranno congruenti, sempre per il
teorema di Talete, i segmenti corrispondenti HG, GD sulla seconda trasversale: HG GD.
f) Dal confronto delle congruenze GHHB, HG GD deduciamo la congruenza dei tre segmenti DG,
GH, HB.
2. Facciamo riferimento alla Figura 2
a) Vogliamo provare che il quadrilatero
EHFG è un parallelogramma.
b) Nel precedente punto 1.c) abbiamo
precisato che AF//EC, dunque GF//EH.
Proviamo che risulta anche GFEH,
dopo di che potremo affermare che il
quadrilatero EHFG è un
parallelogramma per avere due lati
opposti paralleli e congruenti.
Consideriamo la coppia di triangoli
Luigi Lecci: www.matematicaescuola.it
Figura 2
Pagina 1
L2.mat, punto di formazione per Matematica e Fisica
EBH, DGF ed osserviamo che hanno EBDF, HBDG e gli angoli EBH , GDF congruenti
perché coppia di angoli alterni interni rispetto alle parallele AB, DC tagliate dalla trasversale
BD. I due triangoli sono congruenti per il primo criterio, perciò risulta anche EHGF.
c) Osserviamo ora che nel parallelogramma EHFG le diagonali sono EF e GH ed esse si tagliano
scambievolmente nel loro punto medio O. Quindi EF divide GH in due parti congruenti. La
tesi è acquisita.
Luigi Lecci: www.matematicaescuola.it
Pagina 2