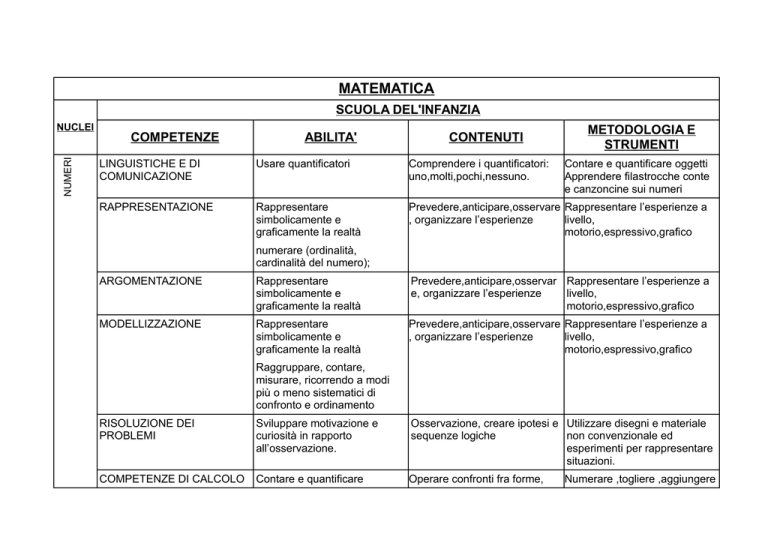
MATEMATICA
SCUOLA DEL'INFANZIA
NUMERI
NUCLEI
COMPETENZE
ABILITA'
CONTENUTI
METODOLOGIA E
STRUMENTI
LINGUISTICHE E DI
COMUNICAZIONE
Usare quantificatori
Comprendere i quantificatori:
uno,molti,pochi,nessuno.
Contare e quantificare oggetti
Apprendere filastrocche conte
e canzoncine sui numeri
RAPPRESENTAZIONE
Rappresentare
simbolicamente e
graficamente la realtà
Prevedere,anticipare,osservare Rappresentare l’esperienze a
, organizzare l’esperienze
livello,
motorio,espressivo,grafico
numerare (ordinalità,
cardinalità del numero);
ARGOMENTAZIONE
Rappresentare
simbolicamente e
graficamente la realtà
Prevedere,anticipare,osservar Rappresentare l’esperienze a
e, organizzare l’esperienze
livello,
motorio,espressivo,grafico
MODELLIZZAZIONE
Rappresentare
simbolicamente e
graficamente la realtà
Prevedere,anticipare,osservare Rappresentare l’esperienze a
, organizzare l’esperienze
livello,
motorio,espressivo,grafico
Raggruppare, contare,
misurare, ricorrendo a modi
più o meno sistematici di
confronto e ordinamento
RISOLUZIONE DEI
PROBLEMI
Sviluppare motivazione e
curiosità in rapporto
all’osservazione.
Osservazione, creare ipotesi e Utilizzare disegni e materiale
sequenze logiche
non convenzionale ed
esperimenti per rappresentare
situazioni.
COMPETENZE DI CALCOLO
Contare e quantificare
Operare confronti fra forme,
Numerare ,togliere ,aggiungere
SPAZIO E FIGURE
Ordinare in successione
colori, quantità e dimensioni
Effettuare semplici operazioni Sviluppare la capacità di
concrete
ordinare, confrontare e
misurare.
Numera correttamente fino a
10
Ripete filastrocche ,conte e
decine.
USO DI SUSSIDI E
STRUMENTI
Confronto numeri e figure,
unità di misure non
convenzionate.
Operano e giocano con
materiali strutturati,
costruzioni, giochi da tavolo di
vario tipo.
LINGUISTICHE E DI
COMUNICAZIONE
riconoscere le principali figure operare confronti tra forme e
dimensioni
geometriche;
RAPPRESENTAZIONE
Interpretare e produrre
simboli, mappe e percorsi
Confrontare, sperimentare
Uso di oggetti non strutturati
giocare con i blocchi logici e
materiale non strutturato
Osservare e creare ipotesi
Fare analisi
Concetti topologici
Giocare con le forme presenti
nell’ambiente
Osservare e fare ipotesi
sull’ambiente che ci circonda
Fare esperimenti, costruire
percorsi.
Confronta ed analizza figure
geometriche, individuando
varianti e relazioni.
ARGOMENTAZIONE
MODELLIZZAZIONE
RISOLUZIONE DEI
PROBLEMI
Sviluppare atteggiamenti di
sicurezza curiosità e
motivazione all’esplorazioni
Individuare strategie per
risolvere problemi.
RELAZI
ONI E
COMPETENZE DI CALCOLO
USO DI SUSSIDI E
STRUMENTI
Utilizzare diversi strumenti per Confrontare ,analizzare
misurare
Fare griglie, piccoli diagrammi
LINGUISTICHE E DI
COMUNICAZIONE
Porre domande,discutere,
confrontare ipotesi,
Confrontare,
raggruppare,relazionare
Eseguire compiti relativialla
vita quotidiana che implichino
conte, oggetti e persone.
FUNZIONI
spiegazioni,soluzioni
RAPPRESENTAZIONE
Raggruppare, ordinare ,seriare Serie e ritmi
oggetti;
Giocare costruendo sequenze
temporali
ARGOMENTAZIONE
MODELLIZZAZIONE
individuare la relazione fra gli
oggetti;
concetto di proporzione
Rappresentazioni grafiche
RISOLUZIONE DEI
PROBLEMI
stabilire la relazione esistente
fra gli oggetti, le persone e i
fenomeni (relazioni logiche,
spaziali e temporali );
percepire e collocare eventi
nel tempo.
Costruire calendario del
tempo, settimanale ,stagioni…
USO DI SUSSIDI E
STRUMENTI
.esplorare e rappresentare lo
spazio utilizzando codici
diversi
Elaborare simboli e mappe
Costruire un calendario del
mese collocandovi rilevazioni
meteorologiche, le assenze,
ecc
LINGUISTICHE E DI
COMUNICAZIONE
elaborare previsioni ed ipotesi Elabora dati
DATI E PREVISIONI
COMPETENZE DI CALCOLO
individua strategie per
risolvere problemi
utilizza un linguaggio
appropiato per discutere
osservazioni ed esperienze.
RAPPRESENTAZIONE
Rappresenta graficamente il
vissuto, storie, sequenze
temporali
ARGOMENTAZIONE
MODELLIZZAZIONE
RISOLUZIONE DEI
PROBLEMI
Fornisce spiegazioni sulle
cose e sui fenomeni
Elabora previsioni ed ipotesi
Atteggiamento curioso
Istaura relazioni
Esplora e gioca con gli
elementi
COMPETENZE DI CALCOLO
USO DI SUSSIDI E
STRUMENTI
Osserva ed elabora previsioni Sequenze logiche
Costruisce grafici,esperimenti
SCUOLA PRIMARIA AL TERMINE DELLA CLASSE TERZA
NUMERI
NUCLEI
COMPETENZE
ABILITA'
LINGUISTICHE E DI
COMUNICAZIONE
Sa:
-contare oggetti o eventi, a voce e
mentalmente, in senso
progressivo e regressivo e per
salti di due, tre, ...
- leggere e scrivere i numeri
naturali in notazione decimale.
- verbalizzare procedure di
calcolo.
RAPPRESENTAZIONE
Sa:
- confrontare e ordinare e
rappresentare i numeri naturali
anche decimali, avendo
consapevolezza della notazione
posizionale;
- eseguire le operazioni con i
numeri naturali con gli algoritmi
scritti usuali.
- rappresentare numeri ed
eseguire semplici addizioni e
sottrazioni, anche con riferimento
CONTENUTI
METODOLOGIA E
STRUMENTI
-Rappresentazione i numeri natu- A livello metodologico si
rali in base dieci con raggruppa- opererà al fine di :
menti, abaco, blocchi
- favorire la costruzione delle
aritmetici multibase.
conoscenze da diversi spunti e
-Antichi sistemi di numerazione e in modi diversi
i numeri romani e confronto con il
- creare un contesto
nostro sistema posizionale decid’apprendimento stimolante e
male
-Riconoscimento. nella scrittura in significativo
base dieci dei numeri. il valore po- - sviluppare un atteggiamento
sizionale delle cifre (valore assolu- positivo verso la matematica
to e relativo).
Gli alunni saranno messi in
-Il significato del numero zero e
condizione di acquisire i
del numero uno e il loro comportaconcetti e le tecniche in modo
mento nelle quattro operazioni.
-Memorizzazione delle tabelline. costruttivo attraverso un
percorso didattico che favorisca
-Ampliamento dal periodo delle
unità semplici al periodo delle mi- la scoperta personale e la
gliaia.
ricerca: è il costante e il
-Esecuzione delle quattro opera- comune lavoro tra insegnante
zioni con e senza cambio, con nu- ed alunni, impegnati in una
meri entro le unità di migliaia (in continua scoperta e nella
riga e in colonna).
raccolta di tutte le sollecitazioni
-Eseguire per iscritto e mentalmatematiche offerte dal mondo,
mente le quattro operazioni tra nu- che promuove la formazione di
meri naturali con metodi, strumenti atteggiamenti di simpatia nei
e tecniche diversi.
confronti di questa disciplina.
-Ipotizzare l'ordine di grandezza
La capacità di dominare il
del risultato per ciascuna delle
quattro operazioni tra numeri natu- linguaggio specifico, sia
nell’aspetto verbale che nelle
rali.
forme espressive simboliche e
-L’addizione e i suoi termini.
Sa:
- Le proprietà (commutativa, asso- grafiche dovrà andare di pari
argomentare percorsi di
ciativa, dissociativa) e il loro uso passo con la costruzione dei
soluzione attraverso parole,
nel calcolo orale e scritto.
concetti. La discussione
schemi o diagrammi.
-L’elemento neutro.
collettiva sarà un buon metodo
-La
sottrazione
e
i
suoi
termini
Sa:
per sviluppare un linguaggio
raccogliere dati e rappresentarli -La proprietà invariantiva.
sempre più adeguato e per
-La sottrazione come operazione
con l'uso di grafici e tabelle
introdurre nuovi concetti come
inversa dell’addizione.
rappresentare graficamente e
pure il ricorso a forme di
-La prova della sottrazione.
simbolicamente un problema
insegnamento reciproco e al
-L'elemento neutro.
Sa:
-Il resto, la differenza, il comple- lavoro in coppie o piccoli
costruire il testo di un problema
gruppi, utile anche per
mento.
partendo da situazioni differenti di -La moltiplicazione: ripasso delle sviluppare la capacità di
esperienza risolvere un problema tabelline.
cooperare.
utilizzando le quattro operazioni; -Il rapporto addizione/moltiplica- Nell'affrontare gli argomenti
zione.
della materia, si approfitterà di
Sa:
-La nozione di prodotto combina- ogni occasione per trovare
eseguire le quattro operazioni
torio.
con i numeri naturali
agganci interdisciplinari,
-Lo zero come termine annullante
provocando negli alunni la
Sa:
e l'uno come elemento neutro.
usare l'abaco, la linea dei numeri, -I termini della moltiplicazione e le curiosità e la formulazione di
il calcolo multibase, la tavola
sue proprietà (commutativa, asso- domande. I concetti matematici
pitagorica
ciativa, dissociativa, distributiva). saranno presentati in modo da
-La moltiplicazione con due cifre al favorire lo sviluppo e
l'organizzazione di strutture
moltiplicatore.
-La divisione:il concetto di ripartialle monete o ai risultati di
semplici misure.
- rappresentare frazioni di oggetti
e forme, individuando l’unità
frazionaria;
- rappresentare graficamente e
simbolicamente un problema
- rappresentare percorsi di
soluzione attraverso parole,
schemi o diagrammi.
ARGOMENTAZIONE
MODELLIZZAZIONE
RISOLUZIONE DEI PROBLEMI
COMPETENZE DI CALCOLO
USO DI SUSSIDI E
STRUMENTI
zione e di continenza.
mentali sempre più complete.
-Ripasso della divisione come
Nei percorsi d’apprendimento si
operazione inversa della moltipli- intende procedere
cazione,
contemporaneamente
-I termini della divisione.
all’allargamento dei contenuti e
-Le proprietà invariantiva e distriall’approfondimento della
butiva e loro uso nel calcolo scritto
comprensione, guidando i
e orale.
-Il significato operativo dello zero e bambini ad acquisire una
sempre maggiore
dell'uno nella divisione.
consapevolezza dei passi fatti
-Multipli e divisori.
-Le moltiplicazioni e le divisioni per e a superare nel tempo
10-100-1000.
eventuali difficoltà.
-Le frazioni: differenza tra lo
Nell’affrontare le situazioni
“spezzare” in parti diverse e il fra- problematiche si avrà cura di
zionare.
rappresentare una stessa
-Uguaglianza ed equivalenza.
situazione con diverse modalità
-Costruzione della definizione di
(verbale, iconica, simbolica)
frazione.
-Scrittura della frazione e termini. cercando di individuare il
contesto più favorevole per la
-Riconoscimento della funzione
del numeratore, denominatore, li- risoluzione; i bambini verranno
guidati a prendere coscienza
nea di frazione.
del proprio ragionamento,
-Le frazioni proprie: significato,
scrittura e rappresentazione.
motivarlo e criticarlo.
-Le unità frazionarie.
Si svolgeranno attività collettive
-Le frazioni complementari.
ed attività individuali a scuola e
-Confronto tra frazioni con lo stes- a casa, utili al consolidamento
so denominatore.
di quanto appreso.
-Collocazione di frazioni, con lo
stesso denominatore, sulla linea STRUMENTI
dei numeri.
-La frazione di un numero.
Si utilizzeranno per gli esercizi
-Le frazioni decimali e sistema de- e gli approfondimenti: il
cimale.
quaderno, il libro di testo o
-Scrittura in forma decimale delle
schede opportunamente
frazioni decimali.
-Dalla frazione decimale al nume- predisposte.
ro decimale.
Si utilizzeranno tabelle, schemi,
-L'uso della virgola.
grafici, diagrammi e software
-Il valore posizionale delle cifre in didattici.
un numero decimale.
Si far uso di materiale
-Scomposizione e ricomposizione
strutturato (abaco, BAM,
di numeri decimali.
-Relazione d'ordine (<,=,>) tra nu- righello, goniometro, squadra,
compasso, bilancia, corda
meri decimali.
-Addizioni e sottrazioni con i nu- metrica, contenitori graduati,
fac-simile di banconote e
meri decimali.
-Moltiplicazioni con i numeri deci- monete) e non strutturato
mali al moltiplicando, al moltiplica- (oggetti di vario tipo, fogli,
tore, ad entrambi i fattori.
cartoncino, carta millimetrata e
-La divisione con il dividendo deci- quadrettata, lucidi ecc).
male , il divisore decimale e con Si far uso altresì di artefatti
entrambi i termini decimali.
culturali quali menù, listini,
-Analisi di situazioni problematiscontrini, etichette di prodotti,
che:produzione del testo di un protabelle orarie e così via.
blema
partendo da immagini e/o dati.
-Strategie e procedure di risoluzione.
-Problemi in ambito di studio e di
esperienze.
-Problemi con possibilità di risposte diverse.
-Individuazione della struttura :le
diverse parti di un enunciato problema (testo,
risoluzione, risposta).
-Riconoscimento della/e domanda/ e dei dati per costruire risposta/e
pertinente/i
-Algoritmo della soluzione (diagramma, operazione).
SPAZIO E FIGURE
-Problemi di tipo additivo, sottrattivo, moltiplicativo, divisivofrazionario.
-Problemi con dati inutili, mancanti
e sovrabbondanti.
-Problemi con due domande e due
o più operazioni,con calcolo frazionario.
LINGUISTICHE E DI
COMUNICAZIONE
RAPPRESENTAZIONE
ARGOMENTAZIONE
Sa:
-descrivere percorsi utilizzando in
modo proprio termini adeguati
(sopra, sotto, destra, sinistra,
davanti, dietro,.....)
-descrivere un ambiente
utilizzando in modo proprio i
riferimenti spaziali rispetto a sé,
agli oggetti, ai componenti
dell'ambiente stesso
-denominare figure piane e solide.
-denominare rette incidenti,
parallele, perpendicolari.
-Mappe, piantine e orientamento.
-Rappresentazione di oggetti
nel piano e nello spazio.
-Semplici figure dello spazio e del
piano I principali enti
geometrici.
-Concetti di sagoma, confine, impronta, profilo, regione.
-Gli oggetti e loro rappresentazione.
-Differenza tra figure solide e figure piane.
-Le principali figure solide e loro riconoscimento nella realtà.
Sa:
-Riconoscimento delle dimensioni
-ricostruire percorsi
nelle figure solide e nelle piane.
-tracciare
rette
incidenti,
-Le figure piane come impronta
parallele, perpendicolari.
della figura solida o loro sviluppo
-riconoscere e costruire l’angolo
in piano.
retto.
-Simmetrie rotazioni e traslazioni.
-riconoscere angoli maggiori e
-Le linee: rette, semirette, segminori dell’angolo retto.
menti.
Sa:
-Rette incidenti, perpendicolari e
-guidare un compagno nello
parallele.
svolgimento di un percorso
-Concetto di perpendicolarità e reutilizzando corretti riferimenti
lazione di equidistanza nel parallespaziali e scelte ottimali rispetto al lismo.
compito assegnato (es. il percorso -L'angolo e il suo punto di origine.
più breve) e motivando le scelte
-L’angolo come risultato della rotazione e l’angolo come parte di un
MODELLIZZAZIONE
Sa:
piano.
-costruire,
disegnare
alcune
-L'ampiezza dell'angolo e il suo rifigure geometriche.
conoscimento, avvio all’uso del
-identificare il perimetro e l'area
goniometro.
in modo induttivo .
- Classificazione degli angoli in
-rappresentare oggetti in una
base alla misura: retto, piatto, acuposizione data, cogliendo
to, ottuso.
elementi
di
riferimento
-Riconoscimento di angoli nella
nell’ambiente;
realtà e rappresentazione di angoli
sul piano.
RISOLUZIONE DEI PROBLEMI Sa:
-Concetto di poligono.
costruire figure piane attivando
-I poligoni: riconoscimento nei poliprocedure semplici di calcolo
goni dei lati e degli angoli.
-Poligoni concavi e convessi.
COMPETENZE DI CALCOLO
Sa:
-calcolare la lunghezza scegliendo -Riconoscimento nei poligoni delle
diagonali e delle mediane.
l'opportuna unità di misura
-Poligoni con e senza simmetria
USO DI SUSSIDI E STRUMENTI Sa:
interna.
-utilizzare il righello
-Classificazione dei poligoni in
-utilizzare modelli di angoli e figure base ai lati e agli angoli.
dati dall'insegnante o costruiti
-Poligoni regolari e irregolari.
autonomamente
-Il sistema metrico decimale:
-Stima e misura.
-La nozione di grandezza.
-La nozione di unità di misura.
-Misurazioni non convenzionali.
-Esperienze di misurazione nella
realtà.
-Cenni di storia della misurazione
e del S.M.D.
-Il metro, il chilogrammo, il
litro:multipli e sottomultipli.
-Le marche.
-Equivalenze e trasformazioni.
R
fatte
LINGUISTICHE E DI
Sa:
-Classificazione di oggetti, figure,
ELAZIONI E FUNZIONI
COMUNICAZIONE
RAPPRESENTAZIONE
ARGOMENTAZIONE
MODELLIZZAZIONE
RISOLUZIONE DEI PROBLEMI
COMPETENZE DI CALCOLO
-scrivere le misurazioni
numeri in base a una
utilizzando i simboli convenzionali. determinata proprietà. -Equivalen-riconoscere multipli e
ze e ordinamenti. -Grandezze disottomultipli delle unità di misura rettamente e inversamente propordi lunghezza.
zionali -Ricerca di regolarità in sequenze di numeri, figure, simboli e
-riconoscere le unità di misura
parole.
convenzionali
-Rappresentazione di fatti e
Sa:
fenomeni attraverso tabelle, grafici
-scegliere le unità di misura
-I connettivi logici: E - O - NON appropriate alle grandezze da
SE -ALLORA. comprensione e
misurare.
uso corretto
dei connettivi logici.
Sa:
-Frasi semplici e composte.
-misurare
lunghezze
con
-Situazioni esemplari: enunciato,
campioni convenzionali e non.
diagrammi, formulazioni in termini
Sa:
di logica
-misurare grandezze lineari
matematica.
usando il metro e i suoi
-Realizzazione di classificazioni
sottomultipli.
con diagrammi di Venn,di Carroll e
ad albero.
Sa:
-calcolare somme e differenze di -Attività di deduzione.
lunghezze, masse e capacità
date in unità di misura uniformi
USO DI SUSSIDI E STRUMENTI Sa:
-misurare grandezze (lunghezza,
tempo) utilizzando sia unità
arbitrarie sia unità e strumenti
convenzionali (metro, orologio...)
DATI E PREVISIONI
LINGUISTICHE E DI
COMUNICAZIONE
Sa:
-usare correttamente i connettivi:
e, o, non.
-usare correttamente i
quantificatori
-utilizzare in situazioni
significative i termini: possibile,
certo, impossibile.
-effettuare semplici rilevazioni
statistiche.
-rappresentare i dati in tabelle
RAPPRESENTAZIONE
Sa:
-classificare numeri, figure,
oggetti in base a una o più
proprietà
ARGOMENTAZIONE
Sa:
-motivare le scelte effettuate
MODELLIZZAZIONE
Sa:
-usare tabelle, diagrammi di
Venn, ad albero e di Carroll.
RISOLUZIONE DEI PROBLEMI
Sa:
-effettuare semplici indagini
statistiche
COMPETENZE DI CALCOLO
Sa:
-riconoscerere empiricamente la
media e la moda
USO DI SUSSIDI E STRUMENTI Sa:Sa:
-utilizzare correttamente gli
strumenti utili alla costruzione di
tabelle e diagrammi, compresi i
colori utilizzati in modo
consapevole per rendere efficace
la rappresentazione
-Tavole di rappresentazione.
-Criteri di registrazione e tabulazione.
-Elementi per la conduzione di una
indagine.
-Tabelle e grafici di vario tipo
(ideogrammi, istogrammi, grafici
atorta...)
-Semplici rilevazioni statistiche legate alla realtà quotidiana.
-Il campione rappresentativo.
-La determinazione della media
aritmetica.
-Lettura e confronto di diagrammi.
-Nozione di vero o di falso.
-Nozione di certo, incerto, possibile, impossibile, probabile.
-Le previsioni
-La definizione quantitativa di probabilità.
-Rappresentazioni grafiche.
-La frequenza.
-La probabilità: casi favorevoli e
casi possibili.
-Elencazione in situazioni combinatorie dei casi possibili.
NUMERI
NUCLEI
SCUOLA PRIMARIA AL TERMINE DELLA CLASSE QUINTA
COMPETENZE
LINGUISTICHE E DI
COMUNICAZIONE
ABILITA'
CONTENUTI
Sa:
• Riconoscimento all'interno di un
-leggere e scrivere numeri
testo dei dati impliciti ed espliciti,
decimali.
delle parole chiave, delle doman-leggere, scrivere i numeri naturali de.
entro il periodo dei miliardi
• Problemi di tipo aritmetico e di
-utilizzare i termini di una frazione tipo geometrico.
(proprie, improprie, apparenti,
• Problemi legati alle frazioni, alle
complementari, equivalenti);
percentuali, alla compravendita,
-costruire il testo di un problema alle misure ed equivalenze,
partendo da situazioni differenti di al peso netto-peso lordo-tara,
esperienza o da operazioni date;• al perimetro e area.
Riconoscimento all'interno di un • Rappresentazione delle figure nei
testo dei dati impliciti ed espliciti, problemi di tipo geometrico.
delle parole
• Scrittura in forma sintetica dei
chiave, delle domande.
dati.
• Problemi di tipo aritmetico e di • Individuazione della relazione tra
tipo geometrico.
dati e domande.
• Problemi legati alle frazioni, alle • Utilizzo di varie tecniche risolutipercentuali, alla compravendita, ve tra cui il diagramma a blocchi e
alle misure
l'espressione.
ed equivalenze, al peso netto• Multipli e divisori.
peso lordo-tara, al perimetro e
• Criteri di divisibilità dei numeri.
area.
• Numeri primi.
• Rappresentazione delle figure
• Consolidamento del valore posinei problemi di tipo geometrico.
zionale delle cifre e ampliamento
• Scrittura in forma sintetica dei
fino alla
dati.
classe dei milioni e dei miliardi.
• Individuazione della relazione tra • Scrittura di numeri interi e decidati e domande.
mali in cifre e lettere.
• Utilizzo di varie tecniche
• Scomposizione e composizione
risolutive tra cui il diagramma a
di un numero secondo la classe.
blocchi e
• Scomposizione e composizione
l'espressione.
di un numero in forma polinomiale.
• Multipli e divisori.
• Ripasso e consolidamento delle
• Criteri di divisibilità dei numeri. frazioni proprie, improprie, appa• Il crivello di Eratostene.
renti, complementari, equivalen• Numeri primi.
ti e decimali.
• Scomposizione di un numero in • Confronto tra frazioni.
fattori primi.
• Trasformazione di frazioni deci• Le potenze.
mali in numeri decimali e vicever• Le potenze del 10.
sa.
• Consolidamento del valore
• Gli zeri necessari e gli zeri superposizionale delle cifre e
flui nei numeri decimali.
ampliamento fino alla
• Ordinamento e confronto tra nuclasse dei milioni e dei miliardi.
meri decimali.
• Scrittura di numeri interi e
• Calcolo della percentuale (scondecimali in cifre e lettere.
to, aumento).
• Scomposizione e composizione • L'Euro, i multipli e i sottomultipli.
di un numero secondo la classe. • Le quattro operazioni con numeri
• Scomposizione e composizione interi e decimali.
di un numero in forma polinomiale. • Ripasso e consolidamento delle
• Ripasso e consolidamento delle conoscenze legate alle proprietà
frazioni proprie, improprie,
delle quattro operazioni.
apparenti,
• Moltiplicazioni e divisioni di nucomplementari, equivalenti e
meri interi e decimali per 10, 100,
decimali.
1000.
• Confronto tra frazioni.
• Cenni sui numeri interi relativi ed
• Trasformazione di frazioni
in particolare i numeri negativi
decimali in numeri decimali e
viceversa.
• Gli zeri necessari e gli zeri
superflui nei numeri decimali.
• Ordinamento e confronto
tra numeri decimali.
• Calcolo della percentuale
(sconto, aumento).
• L'Euro, i multipli e i sottomultipli.
• Le quattro operazioni con numeri
interi e decimali.
• Ripasso e consolidamento delle
conoscenze legate alle proprietà
delle quattro
RAPPRESENTAZIONE
Sa:
- rappresentare e riconoscere
frazioni equivalenti.
- utilizzare numeri decimali,
frazioni e percentuali per
descrivere situazioni quotidiane.
- interpretare i numeri interi
negativi in contesti concreti.
- rappresentare i numeri
conosciuti sulla retta e utilizzare
scale graduate in contesti
significativi
- conoscere sistemi di notazione
dei numeri che sono o sono stati
in uso in luoghi, tempi e culture
diverse dalla nostra.
- costruire il testo di un problema
- risolvere problemi con schemi
opportuni (diagramma a
blocchi,grafici, disegni schemi
vari);
- risolvere problemi utilizzando le
operazioni;
- risolvere semplici problemi con
un’espressione aritmetica;
risolvere problemi di vario tipo
(compravendita, le varie unità di
misura, percentuale,
geometrici...).
ARGOMENTAZIONE
Sa:
-argomentare percorsi di
soluzione attraverso parole,
schemi o diagrammi, sostenendo
le proprie scelte
MODELLIZZAZIONE
Sa:
astrarre la realtà e rappresentarla
con simboli matematici e non
rappresentare graficamente e
simbolicamente un problema
RISOLUZIONE DEI PROBLEMI
Sa:
-risolvere semplici problemi con
un’espressione aritmetica;
-risolvere problemi di vario tipo
(compravendita, le varie unità di
misura, percentuale,
geometrici...).
COMPETENZE DI CALCOLO
Sa:
-eseguire le quattro operazioni
con sicurezza, valutando
l’opportunità di ricorrere al
calcolo mentale, scritto o con la
calcolatrice a seconda delle
situazioni.
-eseguire la divisione con resto
fra numeri naturali;
-stimare il risultato di una
operazione.
-operare con le frazioni e
calcolare la frazione di un
numero;
-trasformare una frazione
decimale in numero decimale e
viceversa;
-operare con i numeri decimali
USO DI SUSSIDI E STRUMENTI Sa:
-usare la squadra, la riga, il
goniometro, il compasso e il
piano quadrettato.
SPAZIO E FIGURE
LINGUISTICHE E DI
COMUNICAZIONE
-utilizzare un linguaggio
specifico: sopra, sotto, davanti,
dietro, dentro, fuori, affianco, di
fronte, simmetrico, speculare,
contorno e perimetro, superficie
-riconoscere, denominare e
classificare figure.
-nominare e classificare i
poligoni
-nominare e classificare
correttamente i triangoli in
riferimento ai lati ed agli angoli.
-usare correttamente i termini
perimetro ed area
-usare correttamente i termini
geometrici (lato, angolo, vertice,
altezza,....
RAPPRESENTAZIONE
Sa:
-riconoscere, distinguere,
utilizzare le rette, distinguendo
tra direzione e verso.
-riconoscere i concetti di confine
e superficie
-classificare le figure piane.
- costruire e classificare i
poligoni.
-riconoscere e tracciare l'altezza
di una figura
-riconoscere e disegnare semplici
simmetrie, rotazioni e traslazioni
utilizzano il piano quadrettato
-effettuare semplici riduzioni ed
ampliamenti in scala utilizzano il
piano quadrettato
ARGOMENTAZIONE
Sa:
-misurare e stimare lunghezze.
• Ripasso dei principali enti geometrici e riconoscimento di figure
solide e piane.
• Acquisizione della terminologia
adatta alla descrizione e classificazione di un
poligono in base ad elementi significativi come angoli, lati, diagonali,
parallelismo, assi di simmetria...
• Le proprietà delle figure geometriche.
• Costruzione e disegno di figure
geometriche, con strumenti opportuni.
• Utilizzo del piano cartesiano per
localizzare punti o figure.
• Consolidamento del concetto di
perimetro.
• Conoscenza di formule per calcolare il perimetro di figure piane.
• Il concetto di area di figure piane.
• Costruzione del metro quadro.
• Multipli e sottomultipli del metro
quadro.
• Figure equiestese ed equiscomponibili.
• Calcolo dell'area di figure piane
conosciute.
• Riconoscimento dell'apotema e
calcolo del numero fisso
• Classificazione e descrizione di
alcune figure solide.
• Trasformazioni geometriche di figure: traslazioni, rotazioni, simmetrie.
-derivare il concetto di unità di
misura convenzionale e di
misurazione di una grandezza da
esperienze concrete
-scegliere adeguate unità di
misura ed operare con esse,
anche sperimentalmente, per
compiere rilevamenti, confronti,
classificazioni …( di lunghezze,
pesi, angoli, superfici, perimetri
…).
-in base alle caratteristiche di lati
ed angoli, classificare
correttamente i poligoni
MODELLIZZAZIONE
Sa:
-usare sistemi informali di
coordinate per trovare i punti
su un piano.
-riconoscere ed utilizzare le
principali unità di misura del
Sistema Internazionale di Misura:
lunghezza, capacità, massa,
superficie.
-padroneggiare il concetto di
lunghezza, perimetro ed area
come grandezze da misurare.
-riconoscere, distinguere,
confrontare, linee, forme e figure,
superfici, angoli.
-costruire le formule per calcolare
l’area dei triangoli, dei
quadrilateri attraverso
esperienze concrete e di
manipolazione
-riconoscere semplici simmetrie,
rotazioni e traslazioni
-riconoscere semplici riduzioni ed
ampliamenti in scala e leggere
correttamente la legenda ad essi
riferita
RISOLUZIONE DEI PROBLEMI
Sa:
-calcolare l’area dei
triangoli, dei quadrilateri e
di altre figure anche per
scomposizioni.
COMPETENZE DI CALCOLO
Sa:
-operare con le unità di misura.
-calcolare il perimetro usando le
formule.
RELAZIONI E FUNZIONI
USO DI SUSSIDI E STRUMENTI Sa:
-utilizzare strumenti e campioni
per misurare
LINGUISTICHE E DI
COMUNICAZIONE
RAPPRESENTAZIONE
ARGOMENTAZIONE
Sa:
-riconoscere e descrivere
regolarità in una sequenza di numeri o di figure
• Classificazione di oggetti, figure,
numeri in base a una
determinata proprietà.
• Equivalenze e ordinamenti.
• Ricerca di regolarità in sequenze
Sa:
di numeri, figure, simboli e parole.
-rappresentare verbalmente la re• Conoscenza e utilizzo dei quantigolarità rilevata in successioni
ficatori e dei connettivi logici.
di numeri, figure, dati
-estendere o trovare i termini
mancanti all’interno di sequenze
ben definite,
-descrivere le relazioni fra termini
adiacenti in una sequenza
Sa:
-rilevare, analizzare, interpretare,
mettere in relazione semplici dati,
costruendo ragionamenti
formulando ipotesi, sostenendo
le proprie idee e
confrontandosi con il punto di
vista degli altri.
MODELLIZZAZIONE
Sa:
-scrivere o scegliere la
regola di una relazione,
deducendola da alcune coppie di
numeri naturali che soddisfano la
relazione
RISOLUZIONE DEI PROBLEMI
Sa:
-risolvere quesiti utilizzando le
competenze acquisite
COMPETENZE DI CALCOLO
Sa:
-eseguire equivalenze.
-trovare il numero o
l’operazione mancante in
un’espressione numerica (es. 17
+ ■ = 29).
DATI E PREVISIONI
USO DI SUSSIDI E STRUMENTI
LINGUISTICHE E DI
COMUNICAZIONE
Sa:
-usare correttamente i
termini: certo, possibile e
probabile.
RAPPRESENTAZIONE
Sa:
-rappresentare e numerare le
combinazioni di una limitata
quantità di oggetti.
ARGOMENTAZIONE
Sa:
-definire le probabilità di un
evento in semplici situazioni.
MODELLIZZAZIONE
Sa:
-raccogliere, organizzare e
registrare i dati.
-costruire e rappresentare
• Problemi logici.
• Raccolta, classificazione e rappresentazione di dati mediante tabelle,
diagrammi, istogrammi e grafici.
• Statistica: la media, la moda.
• La probabilità: eventi certi, eventi
impossibili, eventi probabili , casi
favorevoli
• Prime rappresentazioni
di dati (tabelle, pittogrammi, grafici
a barre, ecc.).
• Caratteri qualitativi e quantitativi.
• Moda, mediana e media aritmetica.
• Istogrammi.
grafici: lineari, ideogrammi,
istogrammi, aerogrammi.
• Diagrammi di vario tipo.
• Evento certo, possibile e
RISOLUZIONE DEI PROBLEMI
Sa:
-calcolare la media aritmetica.
-individuare la moda.
-risolvere problemi utilizzando
tabelle e grafici.
COMPETENZE DI CALCOLO
Sa:
-operare con le unità di misura
impossibile.
• Campione estratto da una popolazione: casuale e non casuale.
• Probabilità di un evento: valutazione della probabilità di eventi
elementari ed equiprobabili. •
Semplici valutazioni di probabilità
di un evento a partire da dati
statistici.
• Il Sistema internazionale di misura.
• Stime e approssimazioni.
• Notazione scientifica
USO DI SUSSIDI E STRUMENTI Sa:
-operare con tabelle, grafici....
AL TERMINE DELLA SCUOLA SECONDARIA DI PRIMO GRADO
NUMERI
NUCLEI
COMPETENZE
LINGUISTICHE E DI
COMUNICAZIONE
ABILITA'
CONTENUTI
Sa:
Numeri Naturali
- riconoscere e leggere in modoLe quattro operazioni e le loro
corretto i numeri reali e laproprietà
simbologia algebrica specifica.
Elevamento a potenza
- comunicare un risultato
Estrazione di radice
aritmetico/algebrico con il
Divisibilità
linguaggio specifico.
Numeri Razionali
- tradurre dal linguaggio naturale Rapporti e Proporzioni
al linguaggio aritmetico/algebrico e Numeri Relativi
viceversa
Numeri Reali
METODOLOGIA E
STRUMENTI
Lezione frontale
Lezione interattiva, articolata con
interventi
Discussione in aula
Laboratorio
Esercitazione individuale
Lavori, esercitazioni di gruppo
Problem solving
Utilizzo di audiovisivi e LIM
Analisi di testi, manuali, depliants,
riviste
Visite guidate
Role play
Brain storming
Ricerca
Correzione in classe di esercizi,
analisi dell’errore, metacognizione
Attenzione alla interdisciplinarietà
come contrasto al sapere
settoriale
STRUMENTI
Libri di testo in uso
Materiale di facile consumo
Riviste
Risorse offerte dalla rete
Utilizzo di supporti informatici
multimediali
Utilizzo della LIM
RAPPRESENTAZIONE
Sa:
- riconoscere e rappresentare i
numeri reali in diversi modi e
collocarli sulla retta orientata.
- collegare la rappresentazione
algebrica e geometrica dei
numeri
- confrontare e ordinare i numeri
reali.
- scrivere in notazione scientifica
i numeri razionali e stabilirne
l'ordine di grandezza.
ARGOMENTAZIONE
Sa:
- motivare un ragionamento, un
risultato e un calcolo.
- capire e interpretare un
ragionamento e un calcolo di un
compagno
- spiegare un concetto
aritmetico/algebrico anche
utilizzando l'evoluzione storica
della matematica.
MODELLIZZAZIONE
Sa:
- riconoscere
e
utilizzare
la
notazione algebrica dei numeri.
- tradurre e generalizzare in
linguaggio algebrico le proprietà
aritmetiche.
tradurre
in
linguaggio
aritmetico/algebrico
una
situazione reale.
RISOLUZIONE DEI
PROBLEMI
Sa
-risolvere problemi utilizzando:
- espressioni aritmetiche
- rapporti, proporzioni e
percentuali
- espressioni algebriche
- uno schema risolutivo efficace,
ordinato e completo
(comprensione, individuazione
dei dati noti e da calcolare,
rappresentazione grafica, scelta
e applicazione della strategia
risolutiva)
Sa:
- scegliere la strategia più
opportuna per risolvere un
problema.
- trasformare un problema reale
in un problema matematico.
- verificare che i risultati
ottenuti siano coerenti con le
informazioni iniziali.
COMPETENZE DI
CALCOLO E VERIFICA DEI
RISULTATI
Sa:
- eseguire le 4 operazioni con
numeri razionali utilizzando le
relative proprietà.
- eseguire operazioni di
elevamento a potenza ed
estrazione di radice utilizzando le
SPAZIO E FIGURE
relative proprietà.
- eseguire operazioni utilizzando
il calcolo algebrico.
- risolvere espressioni
aritmetiche/algebriche con
numeri razionali e potenze
- stabilire l'attendibilità del
risultato.
- stimare il risultato di un
operazione e stabilire l'ordine di
grandezza.
- arrotondare e approssimare per
difetto o per eccesso ad una cifra
prestabilita
USO DI SUSSIDI E
STRUMENTI
Sa utilizzare:
- il libro di testo.
- le tavole numeriche.
- la calcolatrice.
- il foglio elettronico di calcolo.
LINGUISTICHE E DI
COMUNICAZIONE
Sa:
- descrivere figure piane e solide
per
comunicarle
agli
altri,
utilizzando
correttamente
il
linguaggio specifico.
- conoscere e utilizzare
correttamente il significato
geometrico dei seguenti termini:
congruenza, isoperimetria,
equiestensione, equivalenza,
similitudine.
Misura
Geometria euclidea piana
Figure nel piano
Poligoni
Trasformazioni geometriche nel
piano: isometrie e similitudini
Piano cartesiano
Perimetro e area
Teorema di Pitagora
Circonferenza e cerchio
Geometria euclidea solida
Figure solide
Poliedri
Solidi di rotazione
Volume, capacità e peso
specifico di un solido
RAPPRESENTAZIONE
Sa:
riprodurre
gli
elementi
fondamentali,
le
figure
geometriche piane e solide in
modo preciso sul piano euclideo
e sul piano cartesiano.
- riprodurre in scala una figura
assegnata.
- applicare e riconoscere le
trasformazioni geometriche sul
piano e i loro invarianti.
- riprodurre figure simili.
ARGOMENTAZIONE
Sa:
- cogliere e spiegare le proprietà
comuni e non comuni delle figure
piane e solide.
- motivare le formule geometriche
dirette e inverse di figure piane e
solide
- spiegare la sequenza risolutiva
di un problema geometrico
- riflettere sull'evoluzione storica
della geometria e utilizzarla nella
propria argomentazione.
MODELLIZZAZIONE
Sa:
- utilizzare definizioni e proprietà
geometriche delle principali figure
piane e solide
- tradurre un concetto geometrico
in formula o in simboli e
viceversa
- utilizzare correttamente le
formule geometriche per risolvere
un problema
- scegliere e utilizzare una unità
di misura e uno strumento
geometrico
adeguati
per
misurare una grandezza
- distinguere tra grandezza, unità
di misura e strumento di
misurazione.
- utilizzare le formule dirette e
inverse per il calcolo di perimetro,
area e volume
- utilizzare il Teorema di Pitagora
e conoscere la sua dimostrazione
grafica
- utilizzare correttamente il π e
saperlo ricavare induttivamente
da un'esperienza concreta.
RISOLUZIONE DEI
PROBLEMI
Sa risolvere problemi diretti e
inversi di geometria piana e
solida con una o più figure.
Sa:
COMPETENZE DI
CALCOLO E VERIFICA DEI - riconoscere e operare con
grandezze omogenee e non
RISULTATI
omogenee
- verificare che il risultato del
problema sia coerente coi dati
iniziali
USO DI SUSSIDI E
STRUMENTI
Sa:
- utilizzare il libro di testo
- utilizzare righello, squadre e
compasso per disegnare il modo
preciso le figure geometriche
- utilizzare il goniometro che
misurare l'ampiezza degli angoli
- costruire con la carta e
utilizzare modelli di figure piane e
solide
RELAZIONI E FUNZIONI
LINGUISTICHE E DI
COMUNICAZIONE
Sa:
- riconoscere e definire un
insieme, le operazioni e le
relazioni tra essi
- leggere e interpretare tabelle e
grafici
- riconosce e sa descrivere la
relazione tra grandezze
utilizzando correttamente il
linguaggio specifico
- utilizzare i connettivi logici e i
quantificatori cogliendone le
differenze
- utilizzare il linguaggio algebrico
per comunicare una relazione tra
grandezze o tra numeri
RAPPRESENTAZIONE
Sa:
- sa riconoscere e rappresentare
insiemi e operazioni tra essi
- riconoscere l’insieme vuoto,
finito, infinito, singolo,
sottoinsieme e sa costruirne
degli esempi
- costruire una tabella di raccolta
dati
- rappresentare, riconoscere e
analizzare
relazioni
di
proporzionalità diretta e inversa
sul piano cartesiano
- costruire formule algebriche per
esprimere in forma generale
relazioni e proprietà
ARGOMENTAZIONE
Sa:
- interpretare e comunicare i dati
di un grafico o di una tabella
- riconoscere e descrivere le
Insiemi e rappresentazioni
grafiche
Funzioni e grandezze
proporzionali
Relazioni
Logica
Calcolo letterale
Equazioni
Funzioni
funzioni
direttamente
e
inversamente
proporzionali
elencando
proprietà
e
caratteristiche
- confrontare la proporzionalità
diretta e inversa per evidenziare
differenze e invarianti
- argomentare un ragionamento
con esempi e controesempi
- interpretare gformule algebriche
MODELLIZZAZIONE
Sa:
interpretare,
costruire
e
trasformare formule algebriche
per esprimere in forma generale
relazioni e proprietà aritmetiche e
geometriche
- esprimere la relazione di
proporzionalità con
un'uguaglianza di frazioni e
viceversa
- utilizzare il piano cartesiano per
rappresentare relazioni e funzioni
empiriche o ricavate da tabelle e
per studiare dal punto di vista
grafico le funzioni del tipo:
2
n
y=a x ; y=a / x ; y=a x ; y =2
- collegare le prime due funzioni
precedenti con il concetto di
proporzionalità
RISOLUZIONE DEI
PROBLEMI
Sa:
risolvere
problemi
di
proporzionalità diretta e inversa
- risolvere e esplorare problemi
geometrici e aritmetici utilizzando
equazioni di primo grado
DATI E PREVISIONI
COMPETENZE DI
CALCOLO
Sa:
- eseguire le operazioni tra
insiemi (unione e intersezione)
applicandole
a
situazioni
concrete
- operare con monomi, polinomi
ed equazioni di primo grado
USO DI SUSSIDI E
STRUMENTI
Sa utilizzare:
- tavole
- foglio elettronico
- calcolatrice
-piano caresiano
LINGUISTICHE E DI
COMUNICAZIONE
Sa:
Grafici
- riconoscere e interpretare vari
Statistica
tipi di grafici
Probabilità
- comunicare dei risultati dati
sotto forma di tabella o di grafico
- comunicare l'oggetto di studio
della statistica e della probabilità
- comunicare i dati di una
indagine statistica definendone
gli elementi essenziali
- individuare in semplici situazioni
aleatorie se un evento si
semplice o composto
- usare e riconoscerne la
differenza tra le espressioni: è
probabile, è possibile, è certo, è
impossibile
- riconoscere coppie di eventi
complementari, incompatibili,
indipendenti
RAPPRESENTAZIONE
Sa:
- raccogliere e interpretare
informazioni in una tabella
- rappresentare in un grafico
opportuno le rilevazioni
statistiche sia manualmente sia
con l’uso del foglio elettronico
- scegliere opportunamente il
grafico opportuno in relazione al
tipo di rilevazione e al tipo di
tabella
- rappresentare gli eventi aleatori
utilizzando l'insiemistica
ARGOMENTAZIONE
Sa:
-distinguere
tra
indagine
qualitativa e quantitativa
- argomentare su una indagine
statistica o un evento aleatorio
motivando le proprie scelte con
grafici, tabelle, calcoli
- confrontare dati al fine di
prendere decisioni, utilizzando le
distribuzioni delle frequenze e
delle frequenza relative.
MODELLIZZAZIONE
Sa:
- raccogliere e interpretare
informazioni in tabelle e grafici
opportuni
- confrontare eventi aleatori
(sempici, composti)
- individuare differenze e
analogie tra alcuni eventi aleatori
o tra alcune indagini statistiche
RISOLUZIONE DEI
PROBLEMI
Sa:
- risolvere semplici problemi di
indagine statistica e di calcolo
delle probabilità
COMPETENZE DI
CALCOLO
Sa:
- elaborare i dati in un indagine
statistica (calcolare media, moda,
mediana, percentuale, frequenza
relativa, frequenza assoluta)
- calcolare la probabilità di eventi
aleatori semplici e composti
(complementari,
incompatibili,
indipendenti)
USO DI SUSSIDI E
STRUMENTI
Sa utilizzare e interpretare:
- foglio elettronico
- tabelle
- grafici