Teoremi
1
Teorema di Tellegen
Dato un insieme di tensioni e di correnti compatibili col grafo (che
soddisfano rispettivamente le LKT e le LKC), la sommatoria, della
tensione di lato per le correnti di lato è sempre nulla.
2
1
1
2
3
3
4
4
5
LKC
LKT
V1 + V2 − V3 = 0
V4 + V5 − V3 = 0
nodo 1 I1 + I 3 + I 5 = 0
nodo 2
- I1 + I 2 = 0
nodo 3
I 4 + I 2 + I3 = 0
Grafo della rete
PRESCINDE DAI SUOI
COMPONENTI
Nel caso particolare in cui V e I siano le tensioni
e le correnti di lato Tellegen si riduce al
principio di conservazione dell’energia
V e I scelte arbitrariamente,
purché soddisfino le LK
V1 ' = 2 V2 ' = −1 V3 ' = 1 V4 ' = 4 V5 ' = −3
I1 ' = 1 I 2 ' = 1 I 3 ' = −3 I 4 ' = 2 I 5 ' = 2
V1 ' ' = 2 V2 ' ' = 1 V3 ' ' = 3 V4 ' ' = 1 V5 ' ' = 2
I1 ' ' = 2 I 2 ' ' = 2 I 3 ' ' = −3 I 4 ' ' = 1 I 5 ' ' = 1
∑V ' I ' = 0; ∑V ' ' I ' ' = 0; ∑V ' I ' ' = 0; ∑V ' ' I ' = 0;
i =1:5
i
i
i =1:5
i
i
i =1:5
i
i
i =1:5
i
i
2
Sovrapposizione degli effetti
Per un sistema fisico lineare, per il quale cioè causa ed
effetto sono in relazione lineare, si può affermare che l’effetto
complessivo dovuto a più cause è uguale alla somma degli
effetti che ciascuna causa determina singolarmente.
La corrente in un lato della rete dovuta all’azione di n
elementi attivi è la somma algebrica delle correnti circolanti
nello stesso lato dovute agli elementi attivi agenti
separatamente.
La differenza di potenziale
tra due punti delle rete è la
somma algebrica delle differenza di potenziale tra gli stessi
punti dovute agli elementi attivi agenti separatamente.
3
N.B.
Quando si considera agente nella rete un solo generatore,
¾i generatori di tensione devono essere in cortocircuito (E=0)
¾i generatori di corrente devono essere aperti (I=0)
8Ω
4Ω
6V
8Ω
4Ω
4 ⋅8
V1 = 3
= 8V
4+8
V1
3A
V
6V
V = V1 + V2 = 10V
NON VALE PER LE POTENZE
3A
8Ω
4Ω
V2
4
V2 = 6
= 2V
4+8
4
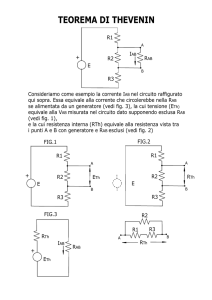
Teorema di Thevenin
Data una rete accessibile da 2 morsetti, formata da generatori e
resistori lineari, ai fini della corrente che circola in un suo
tronco o della tensione ai suoi capi, è sempre possibile
schematizzare la restante rete con un solo generatore ideale di
tensione VTh con in serie una resistenza RTh
A
Rete attiva
lineare
tronco
B
A
VTh
RTh
B
RTh Resistenza relativa
alla stessa rete disattivata
tronco
Vth tensione a vuoto ai
morsetti A e B
5
Dimostrazione
Per il principio di sovrapp. degli effetti
A
VAB= V’AB+ V’’AB
V’AB tensione misurata quando A=0
A V’’ tensione misurata quando i
AB
generatori interni sono disattivati
B
Rete attiva
lineare
A
Rete attiva
V’AB= VAB(0)
Tensione a vuoto
I
Rete
Disattivata
Req= RAB
B
A
A
+ I
RAB
V’’AB
B
-
B
A
A
V’’AB =-RABI
6
VAB= V’AB+ V’’AB= VAB(0)-RABI
VTh=VAB(0)
RTh= RAB
I
VTh
A
RTh
B
VAB= VTh - RThI
7
Teorema di Norton
Data una rete accessibile da 2 morsetti, formata da generatori e
resistori lineari, ai fini della corrente che circola in un suo
tronco o della tensione ai suoi capi, è sempre possibile
schematizzare la restante rete con un solo generatore ideale di
corrente IN con in parallelo una conduttanza GN
A
Rete attiva
lineare
tronco
B
A
IN
GN
tronco
B
GN Conduttanza relativa
alla stessa rete disattivata
IN corrente di cortocircuito
tra i morsetti A e B
8
Dimostrazione
I
A
Rete attiva
lineare
Per il principio di sovrapp. degli
effetti
I= I’+ I’’
I’ corrente misurata quando E=0
I’’ corrente misurata quando i
generatori interni sono disattivati
E
B
I’
Rete attiva
A
I’= ICC
Corrente di cortocircuito
B
I’’ A
Rete
Disattivata
GAB
I’’ A
GAB
E
B
E I’’=-GABE
B
9
I= I’+ I’’=ICC - GABE
I
I = ICC – GAB E
IN
GN
IN
A
tronco
GN
B
I = IN – GN VAB
10
Osservazioni
Æ Un generatore reale di energia può essere
schematizzato indifferentemente come generatore di
tensione (Thevenin) o di corrente (Norton).
VTh
RTh
I
A
V
R
B
Equivalente di Norton
I
IN
GN
V
A
R
B
IN =VTh/ RTh
GN=1/ RTh
11
Teorema di Millmann
Caso limite di rete con due soli nodi
A
R1
E1
R2
E2
Ri
R3
E3
Ei
Rn
En
∑G E
=
∑G
i
V AB
i
i
i
i
B
Il valore della d.d.p esistente tra i 2 nodi di una rete binodale è
quello
espresso
dal
baricentro
delle
conduttanze
caratterizzanti ciascun lato esistente tra i 2 nodi, considerando
le conduttanze in posizione diversa per effetto delle tensioni
dei generatori ideali in serie alle conduttanze stesse.
12
Dimostrazione
A
R1
E1
R2
E2
R3
E3
Ri
Ei
Rn
En
B
Equivalente di Norton
per ciascun ramo
∑G E
=
∑G
i
V AB
i
i
i
i
A
A
G1
B
E1G1
Gn
EnGn
∑G
i
i
B
∑E G
i
i
13
i
TEOREMA DEL MASSIMO TRASFERIMENTO DI POTENZA
a
THEVENIN
RTh
VTh
R
b
I
R
p
b
VTH
p = RI = R ⋅
RTH + R
a
2
pmax
2
RTh
R
Si ha la massima potenza trasferita al carico quando la resistenza del
carico e’ uguale alla resistenza di Thevenin vista dal carico:
R = Rth
Dimostrazione:
2
dp
2 (RTH + R ) − 2 R ( RTH + R )
= VTH
=0 ⇒
4
dR
(RTH + R )
RTH + R − 2 R = 0 ⇒
⇒ pmax =
2
VTH
4RTH
R = RTH
14
1
Rendimento in potenza:
p
η=
p max
R RTH
pcarico
p generatore
Se R = RTH allora:
1
pcarico = pmax
2
VTH
=
4 RTH
p generatore = VTH ⋅ I = VTH
1
⇒ η=
2
2
ETH VTH
=
⋅
RTH + R 2 RTH
IN CONDIZIONI DI MASSIMO TRASFERIMENTO DI POTENZA SI HA
UN RENDIMENTO PARI AL 50%
15