Soluzioni esercizi corrente continua

SOLUZIONE ESERCIZI
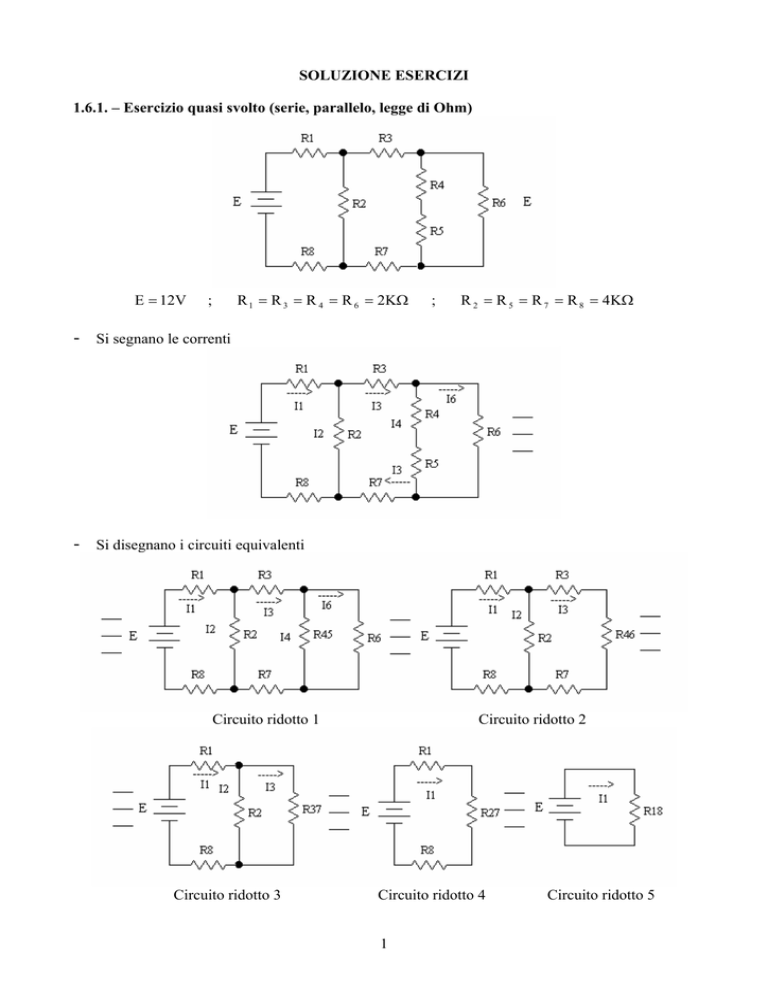
1.6.1. – Esercizio quasi svolto (serie, parallelo, legge di Ohm)
E = 12V
R 1 = R 3 = R 4 = R 6 = 2KΩ
;
-
Si segnano le correnti
-
Si disegnano i circuiti equivalenti
Circuito ridotto 1
Circuito ridotto 3
;
R 2 = R 5 = R 7 = R 8 = 4KΩ
Circuito ridotto 2
Circuito ridotto 4
1
Circuito ridotto 5
-
Calcolo delle resistenze equivalenti
R 45 = R 5 + R 5 = 2 ⋅ 10 3 + 4 ⋅ 10 3 = 6KΩ
R 46 =
;
R4 ⋅R6
6 ⋅ 10 3 ⋅ 2 ⋅ 10 3
= 1,5KΩ
=
R 4 + R 6 6 ⋅ 10 3 + 2 ⋅ 10 3
R 37 = R 3 + R 46 + R 7 = 2 ⋅ 10 3 + 1,5 ⋅ 10 3 + 4 ⋅ 10 3 = 7,5KΩ
R 27
R 2 ⋅ R 37
4 ⋅ 10 3 ⋅ 7,5 ⋅ 10 3
=
= 2,6KΩ
=
R 2 + R 37 4 ⋅ 10 3 + 7,5 ⋅ 10 3
R eq = R 18 = R 1 + R 27 + R 8 = 2 ⋅ 10 3 + 2,6 ⋅ 10 3 + 4 ⋅ 10 3 = 8,6 KΩ
-
Circuito ridotto 5
-
Circuito ridotto 4
I1 =
E
12
=
= 1,395mA
R 18 8,6 ⋅ 10 3
V1 = R 1 ⋅ I1 = 2 ⋅ 10 3 ⋅ 1,395 ⋅ 10 −3 = 2,79V
V27 = V2 = V37 = R 27 ⋅ I1 = 2,6 ⋅ 10 3 ⋅ 1,395 ⋅ 10 −3 = 3,63V
V8 = R 8 ⋅ I1 = 4 ⋅ 10 3 ⋅ 1,395 ⋅ 10 −3 = 5,58V
V2
3,63
=
= 0,908mA
R 2 4 ⋅ 10 3
V37
3,63
=
= 0,484 mA
R 37 7,5 ⋅ 10 3
-
Circuito ridotto 3
I2 =
-
Circuito ridotto 2
V3 = R 3 ⋅ I 3 = 2 ⋅ 10 3 ⋅ 0,484 ⋅ 10 −3 = 0,968V
; I3 =
V46 = V45 = V6 = R 46 ⋅ I 3 = 1,5 ⋅ 10 3 ⋅ 0,484 ⋅ 10 −3 = 0,726 V
V7 = R 7 ⋅ I 3 = 4 ⋅ 10 3 ⋅ 0,484 ⋅ 10 −3 = 1,936 V
-
Circuito ridotto 1
-
Circuito iniziale
I4 =
V45
V
0,726
0,726
=
= 0,121mA ; I 6 = 6 =
= 0,363mA
3
R 45 6 ⋅ 10
R 6 2 ⋅ 10 3
V4 = R 4 ⋅ I 4 = 2 ⋅ 10 3 ⋅ 0,121 ⋅ 10 −3 = 0,242V
V5 = R 5 ⋅ I 4 = 4 ⋅ 10 3 ⋅ 0,121 ⋅ 10 −3 = 0,484 V
Riassumendo
R 18 = 8,6KΩ ; I1 = 1,395mA ; I 2 = 0,908mA ; I 3 = 0,4841mA ; I 4 = 0,121mA
I 6 = 0,363mA ; V1 = 2,79V ; V2 = 3,63V ; V3 = 0,968V ; V4 = 0,242 V ; V5 = 0,0,484 V
V6 = 0,726 V ; V7 = 1,936 V ; V8 = 5,58V
2
1.6.2. – Esercizio facilitato (serie, parallelo, legge di Ohm)
E = 12V
-
;
R 1 = R 3 = R 4 = R 6 = 2KΩ
R 2 = R 5 = R 7 = R 8 = 4KΩ
Si segnano le correnti e si disegnano i circuiti equivalenti
Circuito iniziale
Circuito ridotto 1
Circuito ridotto 2
-
;
Circuito ridotto 3
Circuito ridotto 4
Calcolo delle resistenze equivalenti
R 12 =
R4 ⋅R5
R1 ⋅ R 2
2 ⋅ 10 3 ⋅ 4 ⋅ 10 3
2 ⋅ 10 3 ⋅ 4 ⋅ 10 3
=
Ω
;
R
=
= 1,33KΩ
=
1
,
33
K
=
45
R 4 + R 5 2 ⋅ 10 3 + 4 ⋅ 10 3
R 1 + R 2 2 ⋅ 10 3 + 4 ⋅ 10 3
R 67 = R 6 + R 7 = 2 ⋅ 10 3 + 4 ⋅ 10 3 = 6KΩ
R 37 =
;
R 47 = R 45 + R 67 = 1,33 ⋅ 10 3 + 6 ⋅ 10 3 = 7,33KΩ
R 3 ⋅ R 47
2 ⋅ 10 3 ⋅ 7,33 ⋅ 10 3
= 1,57KΩ
=
R 3 + R 47 2 ⋅ 10 3 + 7,33 ⋅ 10 3
3
R eq = R 18 = R 12 + R 37 + R 8 = 1,33 ⋅ 10 3 + 1,57 ⋅ 10 3 + 4 ⋅ 10 3 = 6,9KΩ
-
Circuito ridotto 4
-
Circuito ridotto 3
I8 =
E
12
=
= 1,793mA
R 18 6,9 ⋅ 10 3
V12 = V1 = V2 = R 12 ⋅ I 8 = 1,33 ⋅ 10 3 ⋅ 1,793 ⋅ 10 −3 = 2,32V
V37 = V3 = V47 = R 37 ⋅ I 8 = 1,57 ⋅ 10 3 ⋅ 1,793 ⋅ 10 −3 = 2,73V
V8 = R 8 ⋅ I1 = 4 ⋅ 10 3 ⋅ 1,793 ⋅ 10 −3 = 6,95V
V3
V
2,73
2,73
=
= 1,365mA ; I 6 = 47 =
= 0,372 mA
3
R 3 2 ⋅ 10
R 47 7,33 ⋅ 10 3
-
Circuito ridotto 2
I3 =
-
Circuito ridotto 1
V45 = V4 = V5 = R 45 ⋅ I 6 = 1,33 ⋅ 10 3 ⋅ 0,372 ⋅ 10 −3 = 0,496 V
V6 = R 6 ⋅ I 6 = 2 ⋅ 10 3 ⋅ 0,372 ⋅ 10 −3 = 0,744 V ; V7 = R 7 ⋅ I 6 = 4 ⋅ 10 3 ⋅ 0,372 ⋅ 10 −3 = 1,488V
-
I1 =
Circuito iniziale
I4 =
V1
V
2,32
2,32
=
= 1,16mA ; I 2 = 2 =
= 0,58mA
3
R 1 2 ⋅ 10
R 2 4 ⋅ 10 3
V
V4
0,496
0,496
=
= 0,248mA ; I 5 = 5 =
= 0,124 mA
3
R 4 2 ⋅ 10
R 5 4 ⋅ 10 3
Riassumendo
R 18 = 6,9KΩ ; I1 = 1,16 mA ; I 2 = 0,58mA ; I 3 = 1,365mA ; I 4 = 0,248mA ; I 5 = 0,124 mA
I 6 = 0,372 mA ; I 8 = 1,379 mA ; V1 = V2 = 2,32 V ; V3 = 2,73V ; V4 = V5 = 0,496 V
V6 = 0,744 V ; V7 = 1,488V ; V8 = 6,95V
1.6.3. – Esercizio (serie, parallelo, legge di Ohm)
E = 12V
;
R 1 = R 3 = R 4 = R 6 = 2KΩ
4
;
R 2 = R 5 = R 7 = R 8 = 4KΩ
-
Si segnano le correnti e si disegnano i circuiti equivalenti
Circuito iniziale
Circuito ridotto 1
Circuito ridotto 2
-
Circuito ridotto 3
Circuito ridotto 4
Calcolo delle resistenze equivalenti
R 12 = R 1 + R 2 = 2 ⋅ 10 3 + 4 ⋅ 10 3 = 6KΩ
R 67 = R 6 + R 7 = 2 ⋅ 10 3 + 4 ⋅ 10 3 = 6KΩ
;
R 45 = R 4 + R 5 = 2 ⋅ 10 3 + 4 ⋅ 10 3 = 6KΩ
R 47 =
;
R 45 ⋅ R 67
6 ⋅ 10 3 ⋅ 6 ⋅ 10 3
= 3KΩ
=
R 45 + R 67 6 ⋅ 10 3 + 6 ⋅ 10 3
R 38 = R 3 + R 47 + R 8 = 2 ⋅ 10 3 + 3 ⋅ 10 3 + 4 ⋅ 10 3 = 9KΩ
R eq = R 18 =
-
Circuito ridotto 4
-
Circuito ridotto 3
-
Circuito ridotto 2
R 12 ⋅ R 38
6 ⋅ 10 3 ⋅ 9 ⋅ 10 3
= 3,6KΩ
=
R 12 + R 38 6 ⋅ 10 3 + 9 ⋅ 10 3
I=
I1 =
E
12
=
= 3,33mA
R 18 3,6 ⋅ 10 3
E
12
=
= 2mA
R 12 6 ⋅ 10 3
;
I3 =
E
12
=
= 1,33mA
R 38 9 ⋅ 10 3
V3 = R 3 ⋅ I 8 = 2 ⋅ 10 3 ⋅ 1,33 ⋅ 10 −3 = 2,67 V
V47 = V45 = V67 = R 47 ⋅ I 3 = 3 ⋅ 10 3 ⋅ 1,33 ⋅ 10 −3 = 4V
V8 = R 8 ⋅ I 3 = 4 ⋅ 10 3 ⋅ 1,33 ⋅ 10 −3 = 5,33V
5
-
Circuito ridotto 1
-
Circuito iniziale
I4 =
V45
V
4
4
=
= 0,67 mA ; I 6 = 67 =
= 0,67 mA
3
R 45 6 ⋅ 10
R 67 6 ⋅ 10 3
V1 = R 1 ⋅ I1 = 2 ⋅ 10 3 ⋅ 2 ⋅ 10 −3 = 4V ; V2 = R 2 ⋅ I1 = 4 ⋅ 10 3 ⋅ 2 ⋅ 10 −3 = 8V
V4 = R 4 ⋅ I 4 = 2 ⋅ 10 3 ⋅ 0,67 ⋅ 10 −3 = 1,34V ; V5 = R 5 ⋅ I 4 = 4 ⋅ 10 3 ⋅ 0,67 ⋅ 10 −3 = 2,68V
V6 = R 6 ⋅ I 6 = 2 ⋅ 10 3 ⋅ 0,67 ⋅ 10 −3 = 1,34V
; V7 = R 7 ⋅ I 5 = 4 ⋅ 10 3 ⋅ 0,67 ⋅ 10 −3 = 2,68V
Riassumendo
R 18 = 3,6KΩ ; I1 = 2mA ; I 3 = 1,33mA ; I 4 = 0,67 mA ; I 6 = 0,67 mA ; V1 = 4V ; V2 = 8V
V3 = 2,57 V ; V4 = 1,34 V ; V5 = 2,68V ; V6 = 1,34V ; V7 = 2,68V ; V8 = 5,33V
1.9.2. - Esercizio da svolgere (generatore equivalente)
Dopo avere risolto il circuito, applicare il principio del generatore equivalente tra i punti A e B, C e
D, E e F. dei circuiti equivalenti ottenuti, calcolare la corrente e la tensione per, rispettivamente, le
resistenze R 4 , R 2 , R 5 .
E = 12V ; R 1 = R 3 = 2KΩ
R 2 = R 5 = 4KΩ ; R 4 = 3KΩ
Risoluzione del circuito
R 12 =
R3 ⋅ R4
R1 ⋅ R 2
2 ⋅ 10 3 ⋅ 3 ⋅ 10 3
2 ⋅ 10 3 ⋅ 4 ⋅ 10 3
=
Ω
;
R
=
= 1,2KΩ
=
1
,
33
K
=
34
R 3 + R 4 2 ⋅ 10 3 + 3 ⋅ 10 3
R 1 + R 2 2 ⋅ 10 3 + 4 ⋅ 10 3
6
I5 =
E
12
=
= 1,836mA
3
R 12 + R 34 + R 5 1,33 ⋅ 10 + 1,2 ⋅ 10 3 + 4 ⋅ 10 3
V12 = V1 = V2 = R 12 ⋅ I 5 = 1,33 ⋅ 10 3 ⋅ 1,836 ⋅ 10 −3 = 2,45V
V34 = V31 = V4 = R 34 ⋅ I 5 = 1,2 ⋅ 10 3 ⋅ 1,836 ⋅ 10 −3 = 2,2V
V5 = R 5 ⋅ I 5 = 4 ⋅ 10 3 ⋅ 1,836 ⋅ 10 −3 = 7,35V
I1 =
V1
2,45
=
= 1,225mA
R 1 2 ⋅ 10 3
;
I2 =
V2
2,45
=
= 0,612 mA
R 2 4 ⋅ 10 3
V3
2,2
=
= 1,1mA
R 4 2 ⋅ 10 3
;
I4 =
V4
2,2
=
= 0,73mA
R 4 3 ⋅ 10 3
I3 =
-
Si applica il principio del generatore equivalente tra i punti A e B
Calcolo di E 0
R 12 =
Eo =
R1 ⋅ R 2
2 ⋅ 10 3 ⋅ 4 ⋅ 10 3
= 1,33KΩ
=
R 1 + R 2 2 ⋅ 10 3 + 4 ⋅ 10 3
R3
2 ⋅ 10 3
12 = 3,27 V
E=
R 12 + R 3 + R 5
1,33 ⋅ 10 3 + 2 ⋅ 10 3 + 4 ⋅ 10 3
Calcolo di I 0
7
Io =
E
12
=
= 2,25mA
R 12 + R 5 1,33 ⋅ 10 3 + 4 ⋅ 10 3
Ro =
Calcolo di R 0
Eo
3,27
=
= 1,45KΩ
Io
2,25 ⋅ 10 −3
Si calcola, per i due circuiti equivalenti ottenuti, la tensione V4 e la corrente I 4 e si confrontano i
valori con quelli già calcolati.
I4 =
Eo
3,27
=
= 0,73mA
R o + R 4 1,45 ⋅ 10 3 + 3 ⋅ 10 3
V4 = R 4 ⋅ I 4 = 3 ⋅ 10 3 ⋅ 0,73 ⋅ 10 −3 = 2,2V
R o4 =
Ro ⋅R4
1,45 ⋅ 10 3 ⋅ 3 ⋅ 10 3
= 0,98KΩ
=
R 0 + R 4 1,45 ⋅ 10 3 + 3 ⋅ 10 3
V4 = R 04 ⋅ I o = 0,98 ⋅ 10 3 ⋅ 2,25 ⋅ 10 −3 = 2,2V
I4 =
V4
2,2
=
= 0,73mA
R 4 3 ⋅ 10 3
I valori coincidono con quelli già calcolati.
-
Si applica il principio del generatore equivalente tra i punti C e D
Calcolo di E 0
R 34
R3 ⋅ R4
2 ⋅ 10 3 ⋅ 3 ⋅ 10 3
=
= 1,2KΩ
=
R 3 + R 4 2 ⋅ 10 3 + 3 ⋅ 10 3
8
Eo =
R1
2 ⋅ 10 3
12 = 3,33V
E=
R 1 + R 34 + R 5
2 ⋅ 10 3 + 1,2 ⋅ 10 3 + 4 ⋅ 10 3
Calcolo di I 0
Io =
Calcolo di R 0
E
12
=
= 2,31mA
3
R 34 + R 5 1,2 ⋅ 10 + 4 ⋅ 10 3
Ro =
Eo
3,33
=
= 1,44KΩ
Io
2,31 ⋅ 10 −3
Si calcola, per i due circuiti equivalenti ottenuti, la tensione V2 e la corrente I 2 e si confrontano i
valori con quelli già calcolati.
I2 =
Eo
3,33
=
= 0,612 mA
R o + R 2 1,44 ⋅ 10 3 + 4 ⋅ 10 3
V2 = R 2 ⋅ I 2 = 4 ⋅ 10 3 ⋅ 0,612 ⋅ 10 −3 = 2,448V
R o2 =
Ro ⋅R2
1,44 ⋅ 10 3 ⋅ 4 ⋅ 10 3
= 1,06KΩ
=
R o + R 2 1,44 ⋅ 10 3 + 4 ⋅ 10 3
V2 = R o 2 ⋅ I o = 1,06 ⋅ 10 3 ⋅ 2,31 ⋅ 10 −3 = 2,446 V
I2 =
I valori coincidono con quelli già calcolati.
9
V2
2,446
=
= 0,612 mA
R 2 4 ⋅ 10 3
-
Si applica il principio del generatore equivalente tra i punti E e F
Calcolo di E 0
E o = E = 12V
Io =
Calcolo di R 0
E
12
=
= 4,74mA
3
R 12 + R 34 1,33 ⋅ 10 + 1,2 ⋅ 10 3
Ro =
Eo
12
=
= 2,53KΩ
Io
4,74 ⋅ 10 −3
Si calcola, per i due circuiti equivalenti ottenuti, la tensione V5 e la corrente I 5 e si confrontano i
valori con quelli già calcolati.
I5 =
Eo
12
=
= 1,837 mA
R o + R 5 2,53 ⋅ 10 3 + 4 ⋅ 10 3
V5 = R 5 ⋅ I 5 = 4 ⋅ 10 3 ⋅ 1,83712 ⋅ 10 −3 = 7,35V
10
R o5 =
Ro ⋅ R5
2,53 ⋅ 10 3 ⋅ 4 ⋅ 10 3
= 1,55KΩ
=
R o + R 5 2,53 ⋅ 10 3 + 4 ⋅ 10 3
V5 = R o 5 ⋅ I o = 1,55 ⋅ 10 3 ⋅ 4,74 ⋅ 10 −3 = 7,35V
I5 =
V5
7,35
=
= 1,836 mA
R 5 4 ⋅ 10 3
I valori coincidono con quelli già calcolati.
Riassumendo I1 = 1,225mA ; I 2 = 0,612 mA ; I 3 = 1,1mA ; I 4 = 0,73mA ; I 5 = 1,836 mA
V1 = V2 = 2,44V ; V3 = V4 = 2,2V ; V5 = 7,35V
punti AB : E o = 3,27 V ; I o = 2,25mA ; R o = 1,45KΩ
punti CD : E o = 3,33V ; I o = 2,31mA ; R o = 1,44KΩ
punti EF : E o = 12V ; I o = 4,74mA ; R o = 2,53KΩ
1.10.2. - Esercizio da svolgere (Thèvenin, Norton)
Trovare la resistenza equivalente R o , secondo Thèvenin e Norton dell’esercizio di paragrafo 1.9.2.
E = 12V ; R 1 = R 3 = 2KΩ
R 2 = R 5 = 4KΩ ; R 4 = 3KΩ
-
Punti A e B
11
Ro =
-
R 12 + R 5 + R 3
=
(1,33 ⋅10
)
+ 4 ⋅ 10 3 ⋅ 2 ⋅ 10 3
= 1,45KΩ
1,33 ⋅ 10 3 + 4 ⋅ 10 3 + 2 ⋅ 10 3
3
Punti C e D
Ro =
-
(R 12 + R 5 ) ⋅ R 3
(
)
⋅ R 1 ⋅ (R 34 + R 5 ) 2 ⋅ 10 3 ⋅ 1,2 ⋅ 10 3 + 4 ⋅ 10 3
= 1,44KΩ
=
R 1 + R 34 + R 5
2 ⋅ 10 3 + 1,2 ⋅ 10 3 + 4 ⋅ 10 3
Punti E e F
R o = R 12 + R 34 =
= 1,33 ⋅ 10 3 + 1,2 ⋅ 10 3 = 2,53KΩ
Riassumendo: punti AB : R o = 1,45KΩ ; punti CD : R o = 1,44KΩ ; punti EF : R o = 2,53KΩ
2.2.2. – Esercizi da svolgere (principi di Kirchhoff)
Risolvere i seguenti circuiti applicando i principi di Kirchhoff.
Esercizio parzialmente risolto
12
E1 = 8V ; E 2 = 12V ; R 1 = R 4 = 2KΩ ; R 2 = R 3 = R 4 = 4KΩ
Vi sono 5 rami, 2 nodi indipendenti e 3 maglie indipendenti.
Si scrivono 2 equazioni ai nodi A e B e 3 equazioni alle maglie ACA, ABCA, BCB:
A:
I1 + I 4 = I 3
ACA :
I 2 = I 4 + I5
B:
E 1 = R 1 I1 + R 3 I 3
ABCA : 0 = −R 3 I 3 − R 4 I 4 + R 5 I 5
BCB :
E 2 = R 2I 2 + R 5I5
⎧I = I − I
3
4
⎪1
⎪I 2 = I 4 + I 5
⎪
⎨R 1 (I 3 − I 4 ) + R 3 I 3 = E 1 ⇒ R 1 I 3 + R 3 I 3 − R 1 I 4 = E 1 ⇒ (R 1 + R 3 )I 3 − R 1 I 4 = E 1
⎪
⎪− R 3 I 3 − R 4 I 4 + R 5 I 5 = 0
⎪R (I + I ) + R I = E ⇒ R I + R I + R I = E ⇒ R I + (R + R )I = E
5 5
2
2 4
2 5
5 5
2
2 4
2
5 5
2
⎩ 2 4 5
Si sostituiscono i valori delle resistenze e delle forze elettromotrici e si risolve il sistema costituito
dalle ultime 3 equazioni.
⎧2 ⋅ 10 3 I 3 + 6 ⋅ 10 3 I 4 = 8
⎪
3
3
3
⎨− 4 ⋅ 10 I 3 − 2 ⋅ 10 I 4 + 4 ⋅ 10 I 5 = 0
⎪
3
3
⎩4 ⋅ 10 I 4 + 8 ⋅ 10 I 5 = 12
⇒
⎧1 ⋅ 10 3 I 3 + 3 ⋅ 10 3 I 4 = 4
⎪⎪
⎨− 2 I 3 − I 4 + 2 I 5 = 0 ⇒
⎪
⎪⎩1 ⋅ 10 3 I 4 + 2 ⋅ 10 3 I 5 = 3
I 4 = −2 I 3 + 2 I 5
Si sostituisce l’espressione di I 4 trovata nelle altre due:
⎧⎪1 ⋅ 10 3 I 3 − 6 ⋅ 10 3 I 3 + 6 ⋅ 10 3 I 5 = 4
⎨
⎪⎩− 2 ⋅ 10 3 I 3 + 2 ⋅ 10 3 I 5 + 2 ⋅ 10 3 I 5 = 3
⇒
⎧⎪− 5 ⋅ 10 3 I 3 + 6 ⋅ 10 3 I 5 = 4
⎨
⎪⎩− 2 ⋅ 10 3 I 3 + 4 ⋅ 10 3 I 5 = 3
⇒
Si moltiplica la prima equazione per 2 e la seconda per 5 e si sottrae membro a membro:
⇒
⎧⎪− 10 ⋅ 10 3 I 3 + 12 ⋅ 10 3 I 5 = 8
⎨
3
3
⎪⎩− 10 ⋅ 10 I 3 + 20 ⋅ 10 I 5 = 15
8 ⋅ 10 3 I 5 = 7
⇒
I5 =
7
= 0,875mA
8 ⋅ 10 3
Sostituendo nella seconda si calcola I 3 :
− 2 ⋅ 10 3 I 3 + 4 ⋅ 10 3 I 5 = 3
⇒
I3 =
4 ⋅ 10 3 I 5 − 3 4 ⋅ 10 3 ⋅ 0,875 ⋅ 10 −3 − 3
=
= 0,23mA
2 ⋅ 10 3
2 ⋅ 10 3
Dalle equazioni ai nodi si calcolano I 4 , I1 e I 2 :
13
I 4 = −2I 3 + 2I 5 = −2 ⋅ 0,25 ⋅ 10 −3 + 2 ⋅ 0,875 ⋅ 10 −3 = 1,25mA
I1 = I 3 − I 4 = 0,25 ⋅ 10 −3 − 1,25 ⋅ 10 −3 = −1mA
I 2 = I 4 + I 5 = 1,25 ⋅ 10 −3 + 0,875 ⋅ 10 −3 = 2,125mA
Il segno meno indica che il verso di I1 è opposto a quello scelto.
Si calcolano le differenze di potenziale:
V1 = R 1 ⋅ I1 = 2 ⋅ 10 3 ⋅ 1 ⋅ 10 −3 = 2V
V2 = R 2 ⋅ I 2 = 4 ⋅ 10 3 ⋅ 2,125 ⋅ 10 −3 = 8,5V
V4 = R 4 ⋅ I 4 = 2 ⋅ 10 3 ⋅ 1,25 ⋅ 10 −3 = 2,5V
V3 = R 3 ⋅ I 3 = 4 ⋅ 10 3 ⋅ 0,25 ⋅ 10 −3 = 1V
V5 = R 5 ⋅ I 5 = 4 ⋅ 10 3 ⋅ 0,875 ⋅ 10 −3 = 3,5V
Riassumendo I1 = 1mA ; I 2 = 2,125mA ; I 3 = 0,25mA ; I 4 = 1,25mA ; I 5 = 0,875mA
V1 = 2V ; V2 = 8,5V ; V3 = 1V ; V4 = 2,5V ; V5 = 3,5V
Esercizio facilitato (principi di Kirchhoff)
E 1 = 8V ; E 2 = 4V ; E 3 = 12V
R 1 = R 3 = 2 KΩ ; R 2 = 4 K Ω
Nel circuito vi sono 3 rami, 1 nodo indipendente e 2 maglie indipendenti. Si scelgono i versi delle
correnti, i versi di percorrenza e si scrive 1 equazione ai nodi (A) e 2 equazioni alle maglie.
14
⎧I 1 + I 3 = I 2 ⇒ I 1 = I 2 − I 3
⎪⎪
⎨E 1 + E 2 = R 1 I1 + R 2 I 2 ⇒ R 1 (I 2 − I 3 ) + R 2 I 2 = E 1 + E 2
⎪
⎪⎩E 2 + E 3 = R 2 I 2 + R 3 I 3 ⇒ R 2 I 2 + R 3 I 3 = E 2 + E 3
⇒
(R 1 + R 3 )I 2 − R 1 I 3 = E1 + E 2
Si sostituiscono i valori delle resistenze e delle forze elettromotrici e si risolve il sistema costituito
dalle ultime 2 equazioni.
⎧⎪6 ⋅ 10 3 I 2 − 2 ⋅ 10 3 I 3 = 12
⎨
3
3
⎪⎩4 ⋅ 10 I 2 + 2 ⋅ 10 I 3 = 16
10 ⋅ 10 3 I 2
= 28
⇒
I2 =
28
= 2,8mA
10 ⋅ 10 3
Sostituendo nella seconda si calcola I 3 :
4 ⋅ 10 3 I 2 + 2 ⋅ 10 3 I 3 = 16
⇒
I3 =
16 − 4 ⋅ 10 3 I 2 16 − 4 ⋅ 10 3 ⋅ 2,8 ⋅ 10 −3
=
= 2,4mA
2 ⋅ 10 3
2 ⋅ 10 3
Dall’equazioni al nodo A si calcola I1 :
Si calcolano le differenze di potenziale:
I1 = I 2 − I 3 = 2,8 ⋅ 10 −3 − 2,4 ⋅ 10 −3 = 0,4mA
V1 = R 1 ⋅ I1 = 2 ⋅ 10 3 ⋅ 0,4 ⋅ 10 −3 = 0,8V
V2 = R 2 ⋅ I 2 = 4 ⋅ 10 3 ⋅ 2,8 ⋅ 10 −3 = 11,2V
V3 = R 3 ⋅ I 3 = 2 ⋅ 10 3 ⋅ 2,4 ⋅ 10 −3 = 4,8V
Riassumendo I1 = 0,4mA ; I 2 = 2,8mA ; I 3 = 2,4mA ; V1 = 0,8V ; V2 = 11,2V ; V3 = 4,8V
Esercizio (principi di Kirchhoff)
E 1 = 8V ; E 2 = 4V
R 1 = R 2 = 2KΩ ; R 3 = 4KΩ
Nel circuito vi sono 3 rami, 1 nodo indipendente e 2 maglie indipendenti. Si scelgono i versi delle
correnti, i versi di percorrenza e si scrive 1 equazione ai nodi (A) e 2 equazioni alle maglie.
15
⎧I = I + I
2
3
⎪⎪ 1
⎨E 1 = R 1 I1 + R 3 I 3 ⇒ R 1 (I 2 + I 3 ) + R 3 I 3 = E 1
⎪
⎪⎩E 2 = R 2 I 2 − R 3 I 3 ⇒ R 2 I 2 − R 3 I 3 = E 2
⇒
R 1 I 2 + (R 1 + R 3 )I 3 = E 1
Si sostituiscono i valori delle resistenze e delle forze elettromotrici e si risolve il sistema costituito
dalle ultime 2 equazioni.
⎧⎪2 ⋅ 10 3 I 2 + 6 ⋅ 10 3 I 3 = 8
⎨
3
3
⎪⎩2 ⋅ 10 I 2 − 4 ⋅ 10 I 3 = 4
2 ⋅ 10 3 I 3 = 4
⇒
I3 =
4
= 0,4mA
10 ⋅ 10 3
Sostituendo nella seconda si calcola I 2 :
2 ⋅ 10 3 I 2 − 4 ⋅ 10 3 I 3 = 4
⇒
I2 =
4 + 4 ⋅ 10 3 I 3 2 + 2 ⋅ 10 3 ⋅ 0,4 ⋅ 10 −3
=
= 2,8mA
2 ⋅ 10 3
1 ⋅ 10 3
Dall’equazioni al nodo A si calcola I1 :
Si calcolano le differenze di potenziale:
I1 = I 2 + I 3 = 2,8 ⋅ 10 −3 + 0,4 ⋅ 10 −3 = 3,2mA
V1 = R 1 ⋅ I1 = 2 ⋅ 10 3 ⋅ 3,2 ⋅ 10 −3 = 6,4V
V2 = R 2 ⋅ I 2 = 2 ⋅ 10 3 ⋅ 2,8 ⋅ 10 −3 = 5,6V
V3 = R 3 ⋅ I 3 = 4 ⋅ 10 3 ⋅ 0,4 ⋅ 10 −3 = 1,6V
Riassumendo I1 = 3,2mA ; I 2 = 2,8mA ; I 3 = 0,4mA ; V1 = 6,4V ; V2 = 5,6V ; V3 = 1,6V
16
2.3.2. – Esercizio da assegnare (sovrapposizione degli effetti)
Del circuito di figura calcolare la corrente I 2 .
E 1 = 8V ; E 2 = 4V ; E 3 = 12V
R 1 = R 3 = 2KΩ ; R 2 = 4KΩ
Si assume quale verso positivo della corrente I 2 quello verso il basso.
I 2 = I 21 + I 22 + I 23 è la somma algebrica dei contributi di E1 , E 2 ed E 3 .
Si cortocircuita E 2 e E 3 e si calcola il contributo I 21 dovuto ad E1 :
R 23
R2 ⋅ R3
4 ⋅ 10 3 ⋅ 2 ⋅ 10 3
=
= 1,33KΩ
=
R 2 + R 3 4 ⋅ 10 3 + 2 ⋅ 10 3
I 21 =
;
R 23
1,33 ⋅ 10 3
V21 =
8 = 3,2V
E1 =
R 1 + R 23
2 ⋅ 10 3 + 1,33 ⋅ 10 3
V21
3,2
=
= 0,8mA
R 2 4 ⋅ 10 3
17
Si cortocircuita E1 e E 3 e si calcola il contributo I 22 dovuto ad E 2 :
R 13 =
R1 ⋅ R 3
2 ⋅ 10 3 ⋅ 2 ⋅ 10 3
= 1KΩ
=
R 1 + R 3 2 ⋅ 10 3 + 2 ⋅ 10 3
I 22 =
;
E2
4
=
= 0,8mA
3
R 13 + R 2 1 ⋅ 10 + 4 ⋅ 10 3
Si cortocircuita E1 e E 2 e si calcola il contributo I 23 dovuto ad E 3 :
R 12
R1 ⋅ R 2
2 ⋅ 10 3 ⋅ 4 ⋅ 10 3
= 1,33KΩ
=
=
R 1 + R 2 2 ⋅ 10 3 + 4 ⋅ 10 3
I 23 =
;
R 12
1,33 ⋅ 10 3
12 = 4,8V
V23 =
E3 =
R 12 + R 3
1,33 ⋅ 10 3 + 2 ⋅ 10 3
V23
4,8
=
= 1,2mA
R 2 4 ⋅ 10 3
Si sommano i tre contributi, tutti con segno positivo, essendo tutti concordi col verso positivo scelto
per I 2 :
I 2 = I 21 + I 22 + I 23 = 0,8 ⋅ 10 −3 + 0,8 ⋅ 10 −3 + 1,2 ⋅ 10 −3 = 2,8mA
18
2.4.2. – Esercizi da assegnare (Millman)
Risolvere applicando Millman
Esercizio N°1
E 1 = 12V ; E 3 = 8V ; E 4 = 4V ; I 2 = 2mA ; R 1 = R 3 = R 4 = 2KΩ ; R 2 = R 5 = 4KΩ
Si calcola VAB :
VAB
E
E1
E4
12
8
4
− I2 + 3 −
− 2 ⋅ 10 −3 +
−
3
3
3
R
R3 R4 + R5
2 ⋅ 10
2 ⋅ 10 + 4 ⋅ 10 3 =
= 1
= 2 ⋅ 10
1
1
1
1
1
1
1
1
+
+
+
+
+
+
3
3
3
3
R1 R 2 R 3 R 4 + R 5
2 ⋅ 10
4 ⋅ 10
2 ⋅ 10
2 ⋅ 10 + 4 ⋅ 10 3
=
I1 : poiché VAB < E 1
⇒
I1 =
6 ⋅ 10 −3 − 2 ⋅ 10 −3 + 4 ⋅ 10 −3 − 0,66 ⋅ 10 −3
⋅ 10 3 = 5,18V
0,5 + 0,25 + 0,5 + 0,66
⇒
I1 esce dal ramo dal punto A e rientra dal punto B ⇒
E 1 − VAB 12 − 5,18
=
= 3,41mA
R1
2 ⋅ 10 3
I2 =
IR2 :
I 3 : poiché VAB < E 3
⇒
I3 =
⇒
;
VAB
5,18
=
= 1,295mA
R2
4 ⋅ 10 3
I 3 esce dal ramo dal punto A e rientra dal punto B ⇒
E 3 − VAB 8 − 5,18
=
= 1,41mA
R3
2 ⋅ 10 3
I 4 : poiché VAB > E 4
⇒
V1 = E 1 − VAB = 12 − 5,18 = 6,82 V
;
V3 = E 3 − VAB = 8 − 5,18 = 2,82V
I 4 entra nel ramo dal punto A ed esce dal punto B ⇒
19
⇒
I4 =
VAB + E 4
5,18 + 4
=
= 1,53mA
R4 + R5
2 ⋅ 10 3 + 4 ⋅ 10 3
V4 = R 4 ⋅ I 4 = 2 ⋅ 10 3 ⋅ 1,53 ⋅ 10 −3 = 3,06V
Riassumendo
;
V5 = R 5 ⋅ I 4 = 4 ⋅ 10 3 ⋅ 1,53 ⋅ 10 −3 = 6,12V
VAB = 5,18V ; I1 = 3,41mA ; I R 2 = 1,295mA ; I 3 = 1,41mA ; I 4 = 1,53mA
Esercizio N°2
E 1 = 8V ; E 2 = 4V ; E 3 = 12V ; R 1 = R 3 = 2KΩ ; R 2 = 4KΩ
Si calcola VAB :
VAB
E1 E 2 E 3
8
4
12
−
+
−
+
3
3
3
R1 R 2 R 3
4 ⋅ 10 −3 − 1 ⋅ 10 −3 + 6 ⋅ 10 −3
2
⋅
10
4
⋅
10
2
⋅
10
=
=
⋅ 10 3 = 7,2V
==
1
1
1
1
1
1
0,5 + 0,25 + 0,5
+
+
+
+
3
3
3
R1 R 2 R 3
2 ⋅ 10
4 ⋅ 10
2 ⋅ 10
I1 : poiché VAB < E 1
⇒
I1 =
I2 =
I1 esce dal ramo dal punto A e rientra dal punto B ⇒
E 1 − VAB 8 − 7,2
=
= 0,4mA
R1
2 ⋅ 10 3
I 2 : poiché VAB > E 2
⇒
⇒
⇒
⇒
V1 = E 1 − VAB = 8 − 7,2 = 0,8V
I 2 entra nel ramo dal punto A ed esce dal punto B ⇒
VAB − E 2 7,2 + 4
=
= 2,8mA
R2
4 ⋅ 10 3
I 3 : poiché VAB < E 3
;
;
V2 = VAB + E 2 = 7,2 + 4 = 11,2 V
I 3 esce dal ramo dal punto A e rientra dal punto B ⇒
20
⇒
I3 =
Riassumendo
E 3 − VAB 12 − 7,2
=
= 2,4mA
R3
2 ⋅ 10 3
V3 = E 3 − VAB = 12 − 7,2 = 4,8V
;
VAB = 7,2V ; I1 = 0,4mA ; I 2 = 2,8mA ; I 3 = 2,4mA
3.4.2. – Esercizi da assegnare (condensatori)
Risolvere i circuiti di figura.
Esercizio 1
E = 12V ; C1 = 20µF ; C 2 = 30µF ; C 3 = 40µF
C eq =
1
1
=
= 9,23µF
1
1
1
1
1
1
+
+
+
+
C1 C 2 C 3
20 ⋅ 10 −6 30 ⋅ 10 −6 40 ⋅ 10 −6
Q = C eq E = 9,23 ⋅ 10 −6 ⋅ 12 = 110,77µC
Q 110,77 ⋅ 10 −6
V2 =
=
= 3,69 V
C2
30 ⋅ 10 − 6
;
;
V1 =
Q 110,77 ⋅ 10 −6
=
= 5,54 V
C1
20 ⋅ 10 − 6
Q 110,77 ⋅ 10 −6
V3 =
=
= 2,77 V
C3
40 ⋅ 10 − 6
E = V1 + V2 + V3 = 5,54 + 3,69 + 2,77 = 12 = E
Esercizio 2
E = 12V ; C1 = 20µF ; C 2 = 30µF ; C 3 = 40µF
C eq = C1 + C 2 + C 3 = 20 ⋅ 10 −6 + 30 ⋅ 10 −6 + 40 ⋅ 10 −6 = 90µF ; Q1 = C1 E = 20 ⋅ 10 −6 ⋅ 12 = 240µC
Q 2 = C 2 E = 30 ⋅ 10 −6 ⋅ 12 = 360µC
;
21
Q 3 = C 3 E = 40 ⋅ 10 −6 ⋅ 12 = 480µC
Q = C eq E = 90 ⋅ 10 −6 ⋅ 12 = 1080µC ; Q 1 + Q 2 + Q 3 = 240 ⋅ 10 −6 + 360 ⋅ 10 −6 + 480 ⋅ 10 −6 = 1080µC
Esercizio 3
E = 12V ; C1 = C 3 = C 5 = 20µF
C 2 = C 4 = C 6 = 40µF
C12 = C1 + C 2 = 20 ⋅ 10
−6
+ 30 ⋅ 10
−6
= 50µF ; C 45
C 4 C5
20 ⋅ 10 −6 ⋅ 30 ⋅ 10 −6
=
=
= 12µF
C 4 + C 5 20 ⋅ 10 −6 + 30 ⋅ 10 −6
C 35 = C 3 + C 45 = 20 ⋅ 10 −6 + 12 ⋅ 10 −6 = 32µF
C16 =
1
1
=
= 11,822µF
1
1
1
1
1
1
+
+
+
+
C12 C 35 C 6 50 ⋅ 10 −6 32 ⋅ 10 −6 30 ⋅ 10 −6
Q = C16 E = 11,822 ⋅ 10 −6 ⋅ 12 = 141,87µC ; V12 = V1 = V2 =
V35 = V3 = V45 =
Q
141,87 ⋅ 10 −6
=
= 2,84 V
C 12
50 ⋅ 10 − 6
Q
141,87 ⋅ 10 −6
Q 141,87 ⋅ 10 −6
;
=
=
4
,
43
V
V
=
=
= 4,73V
6
C 35
C6
32 ⋅ 10 − 6
30 ⋅ 10 − 6
Q 3 = C 3 V3 = 20 ⋅ 10 −6 ⋅ 4,43 = 88,6µC
Q1 = C1 V1 = 20 ⋅ 10 −6 ⋅ 2,84 = 56,8µC
Q 4 = C 45 V45 = 12 ⋅ 10 −6 ⋅ 4,43 = 53,16µC
;
;
22
Q 2 = C 2 V2 = 30 ⋅ 10 −6 ⋅ 2,84 = 85,2µC
V4 =
Q 4 53,16 ⋅ 10 −6
=
= 1,772 V
C4
30 ⋅ 10 − 6
;
V5 =
Q 4 53,16 ⋅ 10 −6
=
= 2,658V
C5
20 ⋅ 10 − 6
V12 + V35 + V6 = 2,84 + 4,43 + 4,73 = 12 = E
Riassumendo C eq = 11,822µF ; Q = 141,87µC ; Q1 = 56,8µC ; Q 2 = 85,2µC ; Q 3 = 88,6µC
Q 4 = 53,16µC ; V1 = V2 = 2,84V ; V3 = 4,43V ; V4 = 1,772 V ; V5 = 2,658V ; V6 = 4,73V
3.5.4. – Esercizi da assegnare (transitori)
Esercizio 1
Del circuito di figura calcolare l’equazione di carica della capacità, supponendola inizialmente
scarica, allorché viene chiuso il tasto T. Dopo un tempo superiore a 5τC (τC è la costante di carica
della capacità) si riapre il tasto T; calcolare l’equazione di scarica della capacità.
E = 10V ; C = 10µF
R 1 = R 2 = 2KΩ
R 3 = R 4 = 4KΩ
Supponendo la capacità inizialmente scarica, si chiude il tasto T. Si applica il teorema di Thèvenin
ai capi della capacità e si riduce il circuito, visto dalla capacità, ad un generatore di tensione.
23
Calcolo di E o
Eo =
=
R3
E=
R1 + R 3 + R 4
4 ⋅ 10 3
⋅ 10 = 4V
2 ⋅ 10 3 + 4 ⋅ 10 3 + 4 ⋅ 10 3
Calcolo di R o
R 14 = R 1 + R 4 = 2 ⋅ 10 3 + 4 ⋅ 10 3 = 6KΩ
R 13 =
;
R 14 ⋅ R 3
6 ⋅ 10 3 ⋅ 4 ⋅ 10 3
=
= 2,4KΩ
R 14 + R 3 6 ⋅ 10 3 + 4 ⋅ 10 3
R o = R 2 + R 13 = 2 ⋅ 10 3 + 2,4 ⋅ 10 3 = 4,4KΩ
Equazione di carica
τ C = R o C = 4,4 ⋅ 10 3 ⋅ 10 ⋅ 10 −6 = 44ms
t
t
t
−
−
⎛
−
⎧t = 5τ C
⎧t = 0
τC
τC
τ
⎜
= Eo 1− e
; ⎨
; v c ( t ) = Vf + (Vi − Vf )e = E o − E o e
⎨
⎜
⎩Vi = 0
⎩Vf = E o = 4V
⎝
⎞
⎟
⎟
⎠
Sostituendo i valori, si ha:
t
−
⎛
−3
v c ( t ) = 4⎜1 − e 44⋅10
⎜
⎝
⎞
⎟ = 4 1 − e − 22, 73 t V
⎟
⎠
(
)
Una volta esaurito il transitorio, ossia quando v c = E o = 4V , si apre l’interruttore T. Inizia un
transitorio di scarica.
24
La capacità, dal valore E o , si scarica, attraverso la resistenza equivalente R 2 + R 3 , fino a zero.
(
)
τ S = R eq C = (R 2 + R 3 )C = 2 ⋅ 10 3 + 4 ⋅ 10 3 ⋅ 10 ⋅ 10 −6 = 60ms
⎧t = 0
⎨
⎩Vi = E o = 4V
Sostituendo i valori, si ha:
;
⎧t = 5τ S
⎨
⎩Vf = 0
v c ( t ) = 4e
v c ( t ) = Vf + (Vi − Vf )e
;
−
−
t
τ
= Eoe
−
t
τS
t
60⋅10 − 3
= 4e −16, 67 t V
Esercizio 2
Dopo avere ridotto il circuito applicando il teorema di Thèvenin ai capi del condensatore, calcolare:
la tensione ai capi del condensatore, esauriti i transitori.
La costante di tempo τ del circuito.
Il tempo minimo dopo il quale si può considerare esaurito il transitorio.
Disegnare il grafico, nel piano V-t, della curva di carica VC del condensatore in funzione del
tempo.
5. Calcolare la differenza di potenziale e la corrente per ogni resistenza.
6. Si inserisce nel circuito un voltmetro per misurare la differenza di potenziale a regime (esauriti i
transitori) ai capi del condensatore. Considerando il voltmetro reale, esso è schematizzabile
come un voltmetro ideale con in serie una resistenza R iv che rappresenta la resistenza interna
del voltmetro. Inserisce lo strumento, equivale ad inserire nel circuito una resistenza
addizionale, per cui la tensione misurata non coincide esattamente con quella calcolata senza
inserire il voltmetro. Utilizzando il valore fornito per R iv , calcolare il valore che si leggerà sul
voltmetro.
1.
2.
3.
4.
E = 10V ; C = 10µF
R 1 = R 2 = 2KΩ
R 3 = R 4 = 4KΩ
25
Calcolo di Eo
Eo =
=
R2
E=
R1 + R 2 + R 3 + R 4
2 ⋅ 10 3
⋅ 10 = 1,67V
2 ⋅ 10 3 + 2 ⋅ 10 3 + 4 ⋅ 10 3 + 4 ⋅ 10 3
Calcolo di Ro
R 14 = R 1 + R 3 + R 4 =
= 2 ⋅ 10 3 + 4 ⋅ 10 3 + 4 ⋅ 10 3 = 10 KΩ
Ro =
R 14 R 2
=
R 14 + R 2
10 ⋅ 10 3 ⋅ 2 ⋅ 10 3
=
= 1,67KΩ
10 ⋅ 10 3 + 2 ⋅ 10 3
VCf = E o = 1,67 V ; τ = R o C = 1,67 ⋅ 10 3 ⋅ 10 ⋅ 10 −6 = 16,7 ms ; ∆t C = 5τ = 5 ⋅ 16,7 ⋅ 10 −3 = 83,33ms
Vc(t)
1,67
83,33⋅10-3
t
Esaurito il transitorio, la capacità equivale ad un circuito aperto. Per calcolare, in tale caso, le
tensioni e le correnti nelle resistenze, si ridisegna il circuito omettendo la capacità C.
26
I=
E
10
=
= 0,833mA
3
3
R 1 + R 2 + R 3 + R 4 2 ⋅ 10 + 2 ⋅ 10 + 4 ⋅ 10 3 + 4 ⋅ 10 3
V1 = R 1 ⋅ I = 2 ⋅ 10 3 ⋅ 0,833 ⋅ 10 −3 = 1,67V
;
V2 = R 1 ⋅ I = 2 ⋅ 10 3 ⋅ 0,833 ⋅ 10 −3 = 1,67V
V3 = R 3 ⋅ I = 4 ⋅ 10 3 ⋅ 0,833 ⋅ 10 −3 = 3,33V
;
V4 = R 4 ⋅ I = 4 ⋅ 10 3 ⋅ 0,833 ⋅ 10 −3 = 3,33V
Inserire un voltmetro, con resistenza interna R iv = 100KΩ , ai capi della capacità C equivale ad
inserire nel circuito una resistenza R iv , che altera i valori di tensione e di corrente dell’intero
circuito, e, quindi, anche il valore di tensione sulla capacità.
Al fine di calcolare il valore letto sul voltmetro, si ridisegna il circuito mettendo al posto della
capacità C la resistenza R iv e calcolando la caduta di tensione su di essa. Analogamente, per tale
scopo si può utilizzare il circuito equivalente calcolato con Thèvenin, mettendo al posto della
capacità (circuito aperto) la resistenza R iv .
VCV =
R iv
100 ⋅ 10 3
E o ==
⋅ 1,67 = 1,642V
R o + R iv
1,67 ⋅ 10 3 + 100 ⋅ 10 3
Il valore misurato risulta leggermente più piccolo del valore reale.
INDICE
SOLUZIONE ESERCIZI
1
1.6.1. – Esercizio quasi svolto (serie, parallelo, legge di Ohm)
1
1.6.2. – Esercizio facilitato (serie, parallelo, legge di Ohm)
3
1.6.3. – Esercizio (serie, parallelo, legge di Ohm)
4
1.9.2. - Esercizio da svolgere (generatore equivalente)
6
1.10.2. - Esercizio da svolgere (Thèvenin, Norton)
11
2.2.2. – Esercizi da svolgere (principi di Kirchhoff)
12
2.3.2. – Esercizio da assegnare (sovrapposizione degli effetti)
17
2.4.2. – Esercizi da assegnare (Millman)
19
3.4.2. – Esercizi da assegnare (condensatori)
21
3.5.4. – Esercizi da assegnare (transitori)
23
27