ESERCIZI DI ELETTROSTATICA - Corsi di Laurea a Distanza

A. Chiodoni – esercizi di Fisica II
QUARTA LEZIONE: dipoli e condensatori
Esercizio 1 (capacità di un condensatore piano)
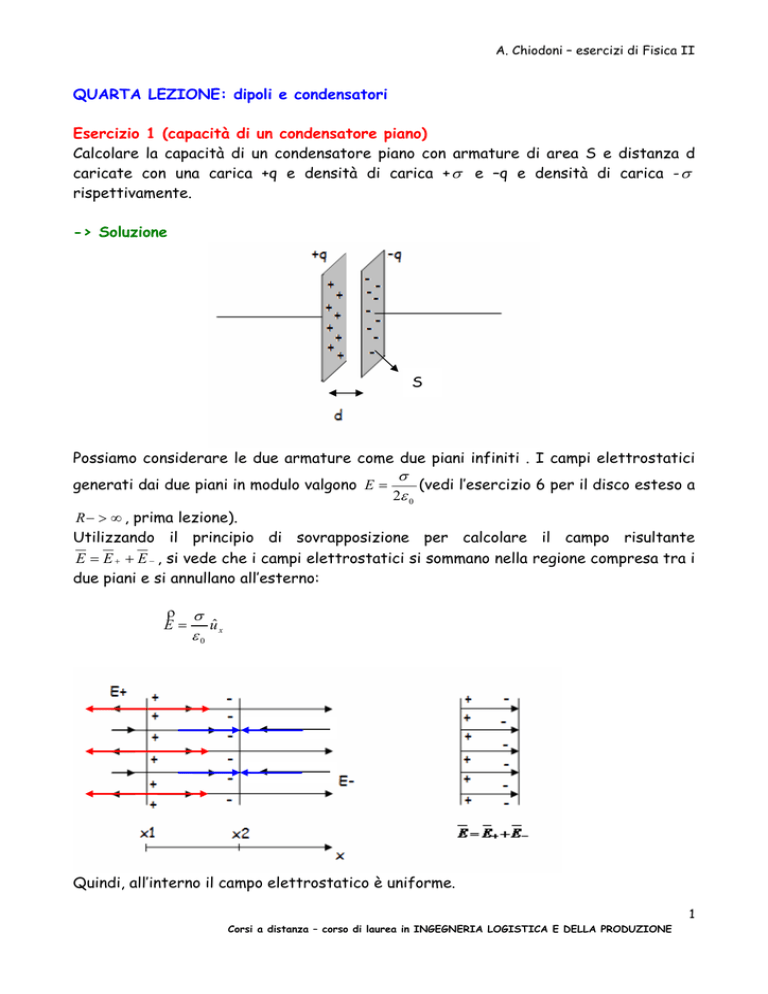
Calcolare la capacità di un condensatore piano con armature di area S e distanza d
caricate con una carica +q e densità di carica + σ e –q e densità di carica - σ
rispettivamente.
-> Soluzione
S
Possiamo considerare le due armature come due piani infiniti . I campi elettrostatici
generati dai due piani in modulo valgono E =
σ
(vedi l’esercizio 6 per il disco esteso a
2ε 0
R − > ∞ , prima lezione).
Utilizzando il principio di sovrapposizione per calcolare il campo risultante
E = E + + E − , si vede che i campi elettrostatici si sommano nella regione compresa tra i
due piani e si annullano all’esterno:
ρ σ
E=
uˆ x
ε0
Quindi, all’interno il campo elettrostatico è uniforme.
1
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Consideriamo ora di determinare la differenza di potenziale tra l’armatura positiva e
un certo punto x interno alle armature:
V1 − V ( x ) =
σ
(x − x1 ) , ricordando che, in generale, V (x ) = − Ex
ε0
La differenza di potenziale tra le due armature sarà allora:
∆V = V1 − V2 =
σ
(x 2 − x1 ) = dσ = Ed = σ S d = qd
ε0
ε0
ε0 S
ε0 S
La capacità del condensatore sarà C =
ε S
q
= 0
∆V
d
Esercizio 2
Ai capi di tre condensatori (partitore capacitivo) c’è una ddp V = VB − V A = 100V e la
capacità equivalente del sistema è C = 100 pF . Calcolare i valori delle capacità C1, C2,
C3, tali che rispetto a V A sia V1 = 50V e V2 = 70V .
-> Soluzione
La carica che si trova su ciascuna armatura vale:
q = CV = 10 × 10 −12 × 10 2 = 10 −18 C
Le singole capacità valgono:
C1 =
q
10 −8
=
= 2 × 10 −10 F = 200 pF
V1 − V A
50
C2 =
q
10 −8
=
= 5 × 10 −10 F = 500 pF
V2 − V1
20
C3 =
q
10 −8
=
= 3.33 × 10 −10 F = 333 pF
V B − V2
30
2
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Esercizio 3 (Capacita’ di un condensatore cilindrico)
Determinare la capacità di un condensatore le cui armature abbiano raggio R1 ed R2,
con R2 > R1, di uguale lunghezza d, grande rispetto ai raggi.
→ Soluzione
Le armature di un condensatore cilindrico sono due porzioni di superficie cilindriche
coassiali, una di raggio R1 e l’altra di raggio R2 > R1, di uguale lunghezza d, grande
rispetto ai raggi. Si realizza cosi un’ulteriore situazione di conduttore al interno di un
altro conduttore cavo, con induzione approssimativamente completa. Se si escludono i
tratti esterni, nell’intercapedine cilindrica tra R1 e R2 il campo elettrostatico è
radiale (vedi esercizio 2, terza lezione):
E (r ) =
λ
u r , con λ densità lineare di carica
2πε 0 r
La differenza di potenziale (d.d.p.) tra le armature è:
ρ ρ
λ
V1 − V2 = ∫ E ⋅ dr =
2πε 0
R1
R2
dr
λ 1
∫R r = 2πε 0 ln r
1
R2
R2
=
R1
R
λ
ln 2
2πε 0 R1
La carica per unità di lunghezza λ è q / d
Quindi, la capacità sarà:
C=
q
=
V1 − V2
λd
R
λ
ln 2
2πε 0 R1
=
2πε 0 d
R
ln 2
R1
3
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Se h = R2 − R1 è molto minore dei raggi, è possibile sviluppare in serie il denominatore
arrestandosi al primo termine:
ln
⎛ R − R1 ⎞ R2 − R1 h
R2
⎟=
=
= ln⎜⎜1 + 2
R1
R1 ⎟⎠
R1
R
⎝
Per cui la capacità diventa:
C=
2πε 0 d R ε 0 S
=
, con S = 2πRd superficie laterale del cilindro.
h
h
Quindi, la capacità per unità di lunghezza è C d =
C 2πε 0
=
R
d
ln 2
R1
E’ possibile realizzare un condensatore cilindrico a capacità variabile facendo
scorrere uno dei due cilindri lungo l’asse, in modo da far variare la lunghezza d.
Esercizio 4
S dispone di 5 condensatori uguali di capacità C. Collegarli in modo che la capacità
totale CTOT sia pari a 3/7C.
-> Soluzione
Poiché il collegamento dei 5 condensatori in serie o in parallelo dà come capacità
totale 0.2C e 5C rispettivamente, per ottenere il valore richiesto dobbiamo ricorrere
ad un collegamento misto serie-paralello. Consideriamo η elementi in serie e µ
elementi in parallelo tra loro e con la serie:
4
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
La capacità totale sarà allora CTO T =
C
η
+ µC
Abbiamo quindi che:
3
⎧C
⎪ + µC = C
7
⎨η
⎪µ + η = 5
⎩
C
η
1
η
+ (5 − η )C =
+ 5 −η =
3
7
3
7
7η 2 − 32η − 7 = 0
⇒
⇒
η1 < 0
η2 > 0
Soluzione non ammissibile.
Se invece proviamo a disporre la serie di η condensatori in serie (e non in parallelo) al
parallelo di µ condensatori:
Si ha:
−1
=
C TOT
1
7
⎧η
=
⎪ +
⎨ C µC 3C
⎪η + µ = 5
⎩
1
1
+
Cη C µ
->
η+
1
7
=
5 −η 3
5
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Risolvendo l’equazione di secondo grado si ottiene η = 2 e µ = 3
Esercizio 5
Un condensatore piano è costruito usando tre differenti materiali dielettrici, come
mostrato in figura. (a) Trovare un espressione per la capacità in funzione dell’area
delle piastre A , della loro distanza d e delle tre costanti dielettriche relative ε r 1 , ε r 2
ε r3 .
(b) Calcolare la capacità usando i valori di A = 1cm 2 , d = 2mm, ε r1 = 4.9, ε r 2 = 5.6, ε r 3 = 2.1 ,
questi ultimi costanti dielettriche rispettivamente di bachelite, vetro Pyrex e teflon.
-> Soluzione
a) Questo condensatore lo possiamo vedere come C1 in parallelo con la serie C23
Le singole capacità saranno:
C1 = ε 1
l / 2⋅ A/ 2
A
= ε1
d
2d
,
C2 = ε 2
l / 2⋅ A/ 2
A
= ε2
d /2
d
,
C3 = ε 3
l / 2⋅ A/ 2
A
= ε3
d /2
d
Mentre la capacità equivalente sarà:
CTOT = C1 + C 23
6
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Dove
C 23 =
⎡ −1
1
1 ⎤
+ ⎥ serie di due capacità.
⎢C 23 =
C 2 C3 ⎦
⎣
C 2 C3
C 2 + C3
Allora:
->
=
CTOT = C1 +
ε ε ⎞
C 2 C3
A ε 2 ε 3⋅ A 2 / d 2
A A ⎛ ε 2ε 3 ⎞ A ⎛ ε 1
⎟⎟ = ⎜⎜ + 2 3 ⎟⎟ =
= ε1
+ ⎜⎜
= ε1
+
C 2 + C3
2d A / d (ε 2 +ε 3 )
2d d ⎝ ε 2 +ε 3 ⎠ d ⎝ 2 ε 2 +ε 3 ⎠
A ⎛ ε 1 (ε 2 + ε 3 ) + 2ε 2 ε 3 ⎞ ε 0 A ⎛ ε r1 (ε r 2 + ε r 3 ) + 2ε r 2 ε r 3 ⎞
⎟⎟
⎜⎜
⎟⎟ =
⎜
ε2 + ε3
ε r2 + ε r3
2d ⎜⎝
⎠
⎠ 2d ⎝
b) Inserendo i valori numerici, si ottiene:
8.85 × 10 −12 × 10 −4 ⎛ 4.9(5.6 + 2.1) + 2 × 5.6 × 2.1 ⎞
−13 ⎛ 37.73 + 23.52 ⎞
C=
⎟=
⎟ = 2.21 × 10 ⎜
⎜
−3
5.6 + 2.1
7.7
2 × 2 × 10
⎠
⎝
⎠
⎝
−13
−12
= 2.21 × 7.95 × 10 = 1.76 × 10 F = 1.76 pF
( ε 0 = 8.8542 × 10 −12 C 2 / Nm 2 )
Esercizio 6
Calcolare in valore e segno la variazione dell’energia elettrostatica di un condensatore
piano, con le armature di area S poste alla distanza d e caricato con una carica Q,
quando si inserisce tra le armature stesse un foglio di materiale dielettrico di
spessore s < d, avente le stessi dimensioni delle armature e caratterizzato dalla
costante dielettrica ε r .
s
d
-> Soluzione
Quando il dielettrico viene inserito nel condensatore esso si polarizza:
7
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
+
d
+
s
x
-
Le superfici superiore ed inferiore del dielettrico in questa situazione equivalgono a
delle sottilissime armature metalliche e quindi potremo considerare il sistema come
costituito da 3 condensatori in serie.
Dunque:
1
CTOT
=
Con
1
1
1
+
+
C1 C 2 C 3
C1 = ε 0
S
S
S
, C 2 = ε 0ε r , C3 = ε 0
d −s−x
s
x
Allora:
1
CTOT
=
ε d − ε r s − ε r x + s + xε r
(d − s − x)
s
x
+
+
= r
ε0S
ε 0ε r S ε 0 S
ε 0ε r S
Infine, la capacità sarà:
C=
ε 0ε r S
ε 0ε r S
=
ε r d − ε r s − ε r x + s + xε r ε r (d − s ) + s
S
.
d
Se la carica del sistema in entrambe le configurazioni è Q, possiamo scrivere le due
energie elettrostatiche iniziale e finale:
Prima di introdurre il dielettrico, la capacità iniziale era pari a C = ε 0
U e ,i =
1 Q2 1 Q2d
=
2 C
2 ε0S
U e, f =
Q 2 [ε r (d − s ) + s ]
1 Q2
=
2 CTOT
2ε 0 ε r S
La variazione d’energia sarà pari a:
8
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
∆U e = U e , f − U e ,i
Q 2 s(1 − ε r )
=
<0
2ε 0 ε r S
in quanto ε r > 1 sempre
Poiché la differenza di energia elettrostatica è negativa, la lastra viene risucchiata
all’interno del condensatore.
Questo risultato è anche indipendente dalla posizione x del dielettrico.
Esercizio 7
Un condensatore a facce piane e parallele, rettangolari di dimensione a e b è
a
parzialmente riempito, per un tratto x = , da una lastra di dielettrico omogeneo ed
3
isotropo di costante dielettrica relativa ε r = 4 . Se la carica totale sull’armatura
superiore è Q = 10 −6 C , quanto vale la carica Q x che si disporre sulla parte di armatura
superiore attaccata al dielettrico?
-> Soluzione
Il sistema dato equivale a due condensatori in parallelo:
C // = C x + C 0
La d.d.p. ∆V tra i punti A e B la posso esprimere in due modi equivalenti:
9
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Qx
Q
Q
=
=
C x C // C x + C 0
∆V =
Se d è la distanza tra le armature, si ha:
Per cui:
C // = C x + C 0 = ε 0 ε r
C x = ε 0ε r
bx
,
d
C0 = ε 0
b(a − x )
d
bx
b(a − x ) ε 0 b
[a + (ε r − 1)x]
+ ε0
=
d
d
d
Allora
Qx =
Cx
C
εrx
Q= x =
Q=
C x + C0
C // a + (ε r − 1)x
4
a
3
a + (4 − 1)
a
3
Q=
4a
2
2
= Q = × 10 −6 C = 6.67 × 10 −7 C
3(a + a ) 3
3
Esercizio 8
Le armature di un condensatore piano sono costituite da piastre quadrate di lato l,
distanti d. Il condensatore viene caricato alla tensione V e successivamente le
armature vengono isolate in modo che la carica su ognuna rimanga costante. (a)
Calcolare l’energia U immagazzinata nel condensatore. Si introduce poi tra le armature
e parallelamente a queste una lamina metallica piana, molto estesa, spessa h. Calcolare:
(b) il lavoro che si deve effettuare per introdurre tale lamina; (c) la nuova tensione V’
tra le armature.
→ Soluzione
(a)
Essendo
la
capacità
del
immagazzinata sarà pari a U =
condensatore
pari
a
C=
ε0S
d
=
ε 0l 2
d
,
l’energia
1
1 ε 0l 2 2
CV 2 =
V .
2
2 d
Dopo che si è inserita la lamina, il sistema è assimilabile ad una serie di due
condensatori uno con distanza x tra le armature e l’altro con distanza d-h-x. I due
condensatori hanno allora capacità:
C1 =
ε 0S
x
e
C2 =
ε0S
d −h−x
da cui
CTOT
⎛ 1
1 ⎞
⎟⎟
= ⎜⎜ +
⎝ C1 C 2 ⎠
−1
⎛ x
d −h− x⎞
⎟
= ⎜⎜
+
ε 0 S ⎟⎠
⎝ ε 0S
−1
=
ε 0l 2
d −h
L’energia immagazzinata dal sistema in questa nuova configurazione sarà:
10
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
U′ =
1
1 Q2
2
′
, dove, poiché la carica sulle armature non cambia, Q è pari a
CTOT V =
2
2 CTOT
Q = CV =
U′ =
ε 0l 2
d
V e quindi
1 ε0 l4 2 d − h 1 2 2 d − h
V
= ε 0l V
2 d2
d2
ε 0l 2 2
2
(b) Il lavoro necessario per inserire la lamina sarà pari a:
W = U −U ′ =
1 l 2 2 ⎛ d − h ⎞ ε 0 l 2h 2
V
ε 0 V ⎜1 −
⎟=
2 d
d ⎠ 2 d
⎝
W è positivo e quindi il lavoro viene fatto dalle forze del campo elettrico che
risucchiano la lamina.
(N.B. Se W fosse stato definito come U’-U si sarebbe trovato che il lavoro era
negativo: infatti nella convenzione W=U’-U si sarebbe avuto per W>0 lavoro subito
dall’esterno, e per W<0 lavoro effettuato dal sistema)
(c) La differenza di potenziale tra le armature del condensatore di partenza in questa
nuova configurazione vale:
V′ =
ε 0 l 2V d − h ⎛ d − h ⎞
Q
=
=⎜
⎟V
CTOT
d ε 0l 2 ⎝ d ⎠
V’<V → la differenza di potenziale tra le armature è diminuita.
Esercizio 9
Un dipolo, di momento elettrico p e momento d’inezia I rispetto ad un asse passante
per il suo centro e ortogonale a p , è immerso in un campo E uniforme. Descrivere il
moto del dipolo quando viene spostato di un piccolo angolo della posizione d’equilibrio.
-> Soluzione
11
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
θ
L’equazione di rotazione, dalla dinamica dei corpi rigidi è:
Proiettando sull’asse di rotazione che è la asse z:
M =
dL
= Iα = p × E .
dt
d 2θ
I 2 = − pE sin θ
dt
Nell’ipotesi d’angolo piccolo, sin θ ≈ θ e l’equazione di rotazione diventa
d 2θ pE
+
θ =0
I
dt 2
Questa è l’equazione di un moto armonico con pulsazione e periodo pari a:
ω=
pE
,
I
T=
2π
ω
= 2π
I
pE
Le leggi orarie dell’angolo e della velocità angolare sono:
θ (t ) = θ 0 sin (ωt + φ ) ,
Ω(t ) =
dθ
= ωθ 0 cos(ωt + φ )
dt
Esercizio 10
Un dipolo elettrico di momento p = 6.3 × 10 −30 Cm si trova al centro di due cariche
positive q1=q2=q= 1.6 × 10 −19 C che distano d = 10 −9 m . Calcolare la forza F che agisce sul
dipolo elettrico.
12
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
-> Soluzione
In questo caso sul dipolo agisce la forza risultante dovuta alla presenza delle due
cariche. Il campo elettrico è non uniforme.
F = q(E 2 − E1 ) = q
∂E
∂E
d=p
∂x
∂x
Il campo elettrico generato delle due cariche e sentito dal dipolo posto al centro è:
q
4πε 0 x 2
1
E1 =
E2 =
(nella posizione generica, Ei =
q
4πε 0 x 2
1
1
q
)
4πε 0 x 2
Poiché esse sono uguali, possiamo calcolare la forza F come:
F=p
∂
(E1 ( x) − E 2 ( x) ) = 2 p ∂E1
∂x
∂x
x=d / 2
Consideriamo a parte la derivata parziale:
∂E1
q ∂ −2
2q − 3
=
x =−
x
∂x
4πε 0 ∂x
4πε 0
( )
e calcoliamo il suo valore nel punto x=d/2:
∂E1
∂x
=−
x=d / 2
2q 1
4πε 0 x 3
=−
x=d / 2
2q 8
4q
=−
3
4πε 0 d
πε 0 d 3
Quindi, la forza F sarà:
⎛
⎞
⎜
⎟
4q ⎟
8 pq
− 8 × 6.3 × 10 −30 ×1.6 × 10 −19
⎜
F = 2 p⎜ −
=
−
=
= −2.90 × 10 −10 N
3 ⎟
3
−12
− 27
3.14 × 8.85 × 10 × 10
πε 0 d
πε 0 d
⎜
⎟
⎜
⎟
⎝
⎠
13
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE