FISICA
Serie 10: Termodinamica X
II liceo
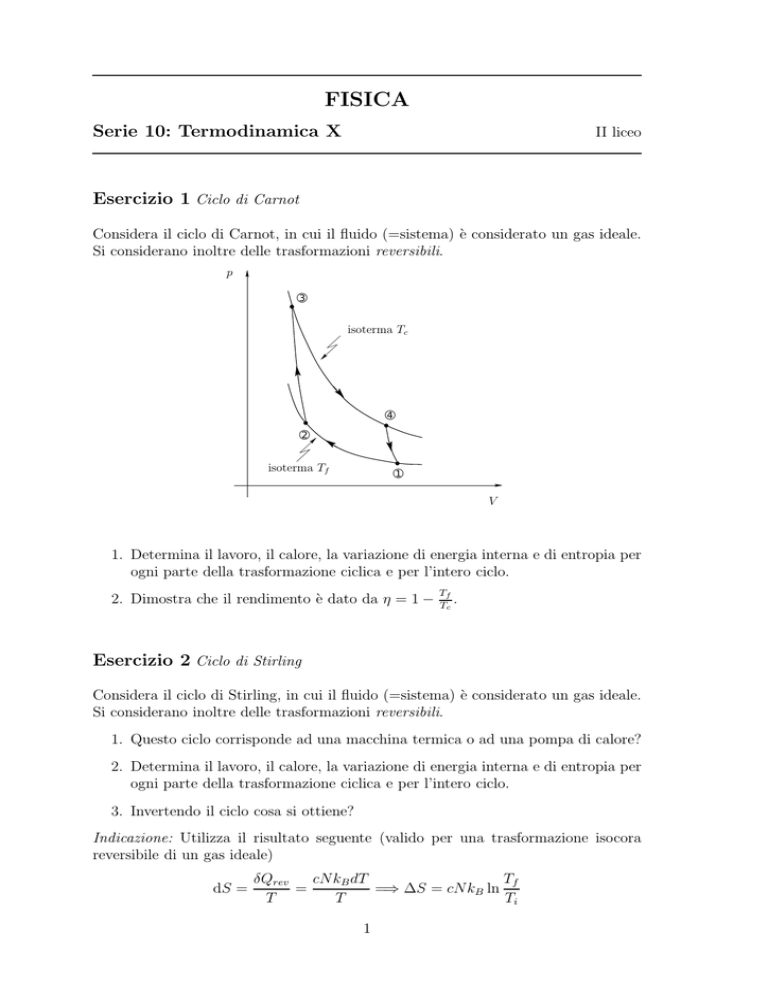
Esercizio 1 Ciclo di Carnot
Considera il ciclo di Carnot, in cui il fluido (=sistema) è considerato un gas ideale.
Si considerano inoltre delle trasformazioni reversibili.
p
➂
isoterma Tc
➃
➁
isoterma Tf
➀
V
1. Determina il lavoro, il calore, la variazione di energia interna e di entropia per
ogni parte della trasformazione ciclica e per l’intero ciclo.
2. Dimostra che il rendimento è dato da η = 1 −
Tf
.
Tc
Esercizio 2 Ciclo di Stirling
Considera il ciclo di Stirling, in cui il fluido (=sistema) è considerato un gas ideale.
Si considerano inoltre delle trasformazioni reversibili.
1. Questo ciclo corrisponde ad una macchina termica o ad una pompa di calore?
2. Determina il lavoro, il calore, la variazione di energia interna e di entropia per
ogni parte della trasformazione ciclica e per l’intero ciclo.
3. Invertendo il ciclo cosa si ottiene?
Indicazione: Utilizza il risultato seguente (valido per una trasformazione isocora
reversibile di un gas ideale)
dS =
δQrev
cNkB dT
Tf
=
=⇒ ∆S = cNkB ln
T
T
Ti
1
p
➁
isoterma Tc
➀
➂
isoterma Tf
➃
V
o l’espressione S(T ) ricavata per dalla relazione fondamentale del gas ideale.
Esercizio 3 Macchine termiche e pompe di calore
1. Una macchina di Carnot lavora tra due bagni termici a 873 K e 573 K. In un
ciclo essa assorbe 80 J nella modalità calore dal termostato caldo.
(a) Qual è il rendimento di questa macchina?
(b) Quanto lavoro viene compiuto in un ciclo?
(c) Quanta energia viene ceduta al bagno termico freddo, nella modalità
calore, in un ciclo?
2. In un ciclo una pompa di calore assorbe 15 kJ da un bagno termico freddo e
cede 20 kJ ad un bagno termico caldo. Quanto lavoro bisogna fornire in un
ciclo?
3. Una macchina termica a vapore ha rendimento pari al 3%. Il vapore viene
immesso nella macchina a 130 oC e viene espulso a 110 oC. Quale percentuale
dell’energia viene perduta rispetto a quella che potrebbe essere teoricamente
utilizzata se il ciclo eseguito dalla macchina fosse perfettamente reversibile?
4. Quando in una macchina termica si usa come fluido il vapor d’acqua, le temperature Tf e Tc alle quali avviene lo scambio di calore si possono considerare,
rispettivamente, la temperatura ambiente (circa 293 K) e la temperatura del
vapore. Calcolare il rendimento massimo della macchina nel caso in cui il vapore possieda come temperatura massima quella corrispondente al suo stato
di ebollizione a pressione ordinaria (373 K). In un motore a vapore reale si
riesce, con particolari accorgimenti, a elevare la temperatura del fluido che
scambia calore fino a 773 K. Calcolare il rendimento massimo in questo caso.
Commenta.
2
Esercizio 4 Più macchine termiche
In una macchina termica reversibile opera tra una sorgente di calore calda a temperatura 890 K e una fredda a temperatura 670 K. La macchina assorbe una quantità
di calore pari a 4800 J. La sorgente a 670 K viene utilizzata come sorgente calda
di un’altra macchina reversibile che usa il calore ceduto dalla prima macchina per
generare ulteriore lavoro. Il calore ceduto dalla seconda macchina scambiato con una
sorgente alla temperatura di 420 K. Determina:
1. Determina il lavoro totale generato dalle due macchine: Wtot = W1 + W2 .
2. Determina il lavoro generato da una macchina termica operante tra le temperature 890 K e 420 K. Conclusione?
Esercizio 5 Produzione di entropia e lavoro nelle macchine termiche
Una macchina termica irreversibile opera tra una sorgente ad alta temperatura
Tc = 810 K, e una sorgente a bassa temperatura Tf = 320 K. Durante ogni ciclo
completo la macchina preleva 660 J di calore dal serbatoio caldo e compie 250 J di
lavoro.
1. Calcola la variazione totale di entropia in un ciclo ∆Stot = ∆S Σ + ∆S sorgenti .
2. Quanto lavoro si otterrebbe nel caso di una macchina reversibile che operasse
alle stesse temperature e prelevasse la stessa quantità di calore?
T′
3. Quanto vale il rapporto Tf′ dove Tf′ e Tc′ sono le temperature del gas (=Σ)
c
alle quali esso scambia calore? Qual è l’origine dell’irreversibilità di questa
macchina termica?
4. Dimostra che la differenza tra il lavoro compiuto dalla macchina irreversibile
e quella reversibile è pari a
− Wrev − Wirr = Tf ∆Stot
dove ∆Stot ha origine nella produzione di entropia (perché?).
Esercizio 6 Efficienza di una pompa di calore
Distinguiamo due casi:
• Per un frigorifero dobbiamo rimuovere la maggior quantità di calore dalla sorgente fredda con il minimo lavoro. Si definisce quindi l’efficienza (o
coefficiente di prestazione – COP) di un frigorifero come
εf =
3
Qf
.
W
• Per una termopompa dobbiamo aggiungere la maggior quantità di calore alla sorgente calda con il minimo lavoro. Si definisce quindi l’efficienza (o
coefficiente di prestazione – COP) di una termopompa come
εc =
−Qc
.
W
1. Una pompa di calore con efficienza pari a 3,5 fornisce 2500 J di calore ad una
stanza. Quanto lavoro è necessario?
2. Dimostra che nel caso reversibile
εc =
Tc
1
=
Tc − Tf
ηrev
e
εf =
Tf
Tc − Tf
3. Le termopompe più efficienti hanno un’efficienza di 5. Di quale fattore si riduce
il consumo di energia elettrica rispetto ad un riscaldamento elettrico?
4. Per mantenere una casa alla confortevole temperatura di 21 o C, quanto la
temperatura esterna è di −3 o C, una pompa di calore fa fluire nella casa energia
alla potenza termica 11 kW = 11 kJ/s. Supponendo che la termopompa abbia
un rendimento pari a quello di una macchina termica ideale, determina la
potenza elettrica per mantenere la casa calda.
Esercizio 7 Macchina termica ad un bagno termico
Considera una macchina termica, nella quale il fluido (=sistema, per esempio vapore)
scambia calore (Q) unicamente con un bagno termico alla temperatura T . Sia W
lavoro associato a questo processo.
T
Q
W
Σ
1. Dai primi due princı̀pi dimostra che per il ciclo
Q
+ ∆i Sciclo = 0 .
T
Q+W =0
2. In un ciclo quanto lavoro può fornire la macchina all’esterno?
3. È possibile avere una macchina termica funzionante con un solo bagno termico?
4
Esercizio 8 Enunciati storici del II principio della termodinamica
Abbiamo visto che esistono due enunciati storici del II principio, dovuti a Kelvin
e Clausius. In questo esercizio ci interessiamo ad essi in relazione alla formulazione
moderna del II principio con il concetto di entropia.
1. Enuncia la formulazione di Kelvin del II principio e dimostrala partendo dal
principi della termodinamica visti in classe.
2. Enuncia la formulazione di Clausius del II principio e dimostrala partendo dal
principi della termodinamica visti in classe.
3. Dimostra l’equivalenza dei due enunciati storici.
Indicazione: Procedi con la logica (A ⇒ B) equivalente a (B ⇒ A).
5












