ESERCIZI SULLA DINAMICA DI CORPI RIGIDI.

5
ESERCIZI SULLA DINAMICA DI CORPI
RIGIDI.
Risoluzione mediante le equazioni cardinali della dinamica, teorema di
conservazione dell’energia meccanica e teorema dell’energia cinetica.
Esercizio n.13
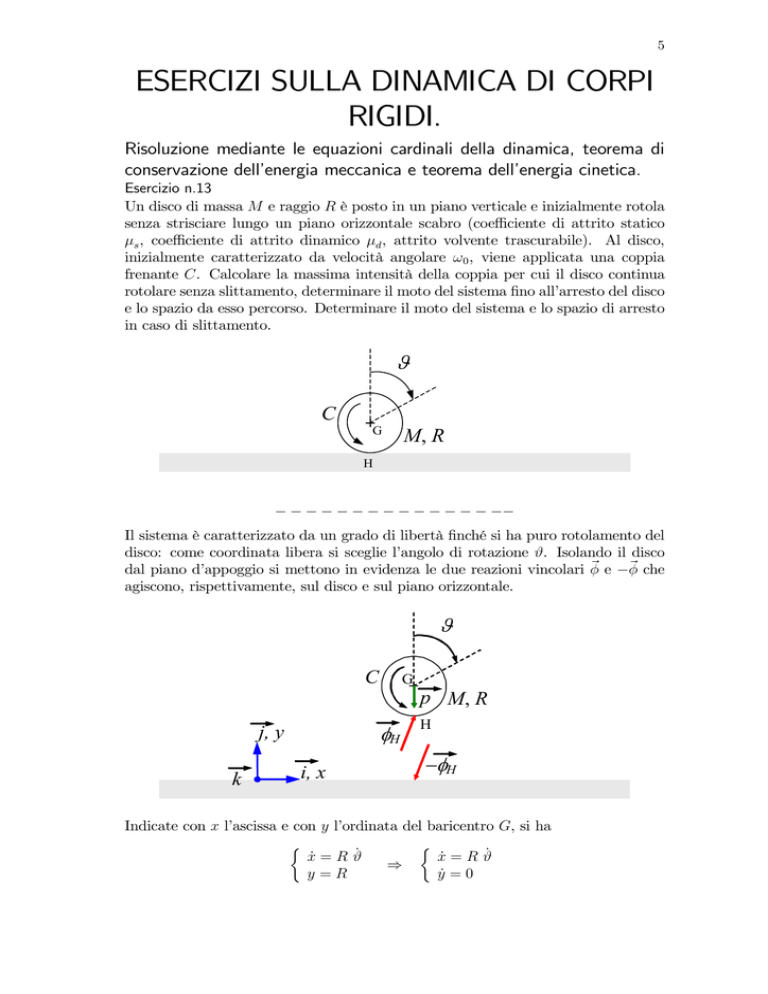
Un disco di massa M e raggio R è posto in un piano verticale e inizialmente rotola
senza strisciare lungo un piano orizzontale scabro (coefficiente di attrito statico
µs , coefficiente di attrito dinamico µd , attrito volvente trascurabile). Al disco,
inizialmente caratterizzato da velocità angolare ω0 , viene applicata una coppia
frenante C. Calcolare la massima intensità della coppia per cui il disco continua
rotolare senza slittamento, determinare il moto del sistema fino all’arresto del disco
e lo spazio da esso percorso. Determinare il moto del sistema e lo spazio di arresto
in caso di slittamento.
ϑ
C
G
M, R
H
− − − − − − − − − − − − − − −−
Il sistema è caratterizzato da un grado di libertà finché si ha puro rotolamento del
disco: come coordinata libera si sceglie l’angolo di rotazione ϑ. Isolando il disco
dal piano d’appoggio si mettono in evidenza le due reazioni vincolari φ e −φ che
agiscono, rispettivamente, sul disco e sul piano orizzontale.
ϑ
C
φH
j, y
k
G
i, x
p M, R
H
−φH
Indicate con x l’ascissa e con y l’ordinata del baricentro G, si ha
½
½
ẋ = R ϑ̇
ẋ = R ϑ̇
⇒
y=R
ẏ = 0
6
Le equazioni cardinali della dinamica sono, prendendo come polo il baricentro G:
(
M aG = φH + p
³ ´
³−−−−→´
→
−
Γ̇ G = MG ⇒ IG ϑ̈ −k = C + H − G ∧ φH
Utilizzando il riferimento cartesiano evidenziato nella figura precedente si possono
dare le seguenti definizioni:
⎧
⎪
aG = ẍ i + ÿ j = ẍ i
⎪
⎪
⎪
⎪
⎪
⎨ φH = φt i + φn j
p = −M g j
⎪
⎪
C
= C k´
⎪
³−−
⎪
⎪
−→
⎪
⎩ H−
− G = −R j
Proiettando la prima equazione vettoriale secondo le direzioni i e j e la seconda
nella direzione k si ricava il seguente sistema:
⎧
⎪
⎨ M aG × i = φH × i + p × i ⇒ M ẍ = φt
M aG³× j ´= φH × j + p × j³ ⇒ 0´= φn − M g
⎪
−−−→
⎩ I ϑ̈ −k × k = C × k + −
H − G ∧ φH × k ⇒ −IG ϑ̈ = C + φt R
G
ovvero:
⎧
⎨ φt = M ẍ
φ =M g
⎩ 1n
M R2 Rẍ = −C − φt R
2
Sostituendo φt fornito dalla prima equazione nella terza si ricava:
⎧
⎨ φt = M ẍ
φ =M g
⎩ 3n
M R ẍ = −C
2
Si noti che l’ultima equazione era immediatamente ottenibile mediante la derivata
del momento della quantità di moto rispetto al punto H e ricordando che ẍ = R ϑ̈:
³ ´ )
→
−
→
−
Γ̇ H = 32 M R2 ϑ̈ −k
× k 3
Γ̇ H = MH ⇒ M R2 ϑ̈ = −C
2
MH = C k
Integrando la terza equazione del sistema si ricava:
⎧
⎨ φt = − 23 CR
φ =M g
⎩ n
x (t) = − 3MC R t2 + A1 t + A2
Le due costanti di integrazione si determinano con le condizioni iniziali; assumendo
che nell’istante iniziale l’origine del sistema di riferimento sia sulla verticale per il
baricentro si ha:
½
½
x (0) = 0
A2 = 0
⇒
A
ẋ (0) = R ϑ̇ (0) = R ω0
1 = R ω0
7
⎧
⎨ φt = − 23 CR
φ =M g
⎩ n
x (t) = − 3MC R t2 + ω0 R t
La massima intensità della coppia C che garantisce il rotolamento è quello per cui
la disuguaglianza di Coulomb rimane strettamente soddisfatta:
2C
3
< µs M g ⇒ C < µs M g R
3R
2
|φt | = −φt < µs φn ⇒
ovvero
3
Cmax = µs M g R
2
Per determinare l’istante ts in cui si ha l’arresto del disco si impone:
ẋ (t) = 0
⇒
ẋ (t) = −
2C
t + ω0 R = 0
3M R
⇒
ts =
3MR2 ω0
2C
e lo spazio L di arresto risulta pari a:
µ
¶2
3MR3 ω 20
3MR2 ω 0
C
3MR2 ω 0
=
+ ω0 R
L = x (ts ) − x (0) = −
3M R
2C
2C
4C
Detta v0 = R ω 0 la velocità iniziale del baricentro G, il minimo spazio di arresto
Ls nel caso di puro rotolamento del disco è il seguente:
Ls =
con:
3 M R v02
1 v02
=
4 Cmax
µs 2g
⎧
⎨ φt = −µs M g
φ =M g
2
⎩ n
x (t) = −µs g t2 + v0 t
Se invece si applica C > Cmax si ha lo slittamento del disco; il sistema è allora
caratterizzato da due gradi di libertà, ad esempio x e ϑ. Lo slittamento è caratterizzato dal coefficiente di attrito dinamico µd e le equazioni cardinali del moto
sono le tre seguenti, a cui occorre aggiungere l’equazione di Coulomb per l’attrito
dinamico in cui, a seguito dello slittamento, si ha φt < 0 cioè |φt | = −φt :
⎧
⎧
φ = −µ M g
M
ẍ
=
φ
⎪
⎪
t
⎪
⎪
⎨ φt = M dg
⎨ 0=φ −M g
n
n
⇒
1
I
ϑ̈
=
−C
−
φ
R
M
R2 ϑ̈ = −C + µd M g R
⎪
⎪
t
⎪
⎪
⎩ 2
⎩ G
−φt = µd φn
ẍ = −µd g
Si noti che alle quattro equazioni corrispondono le quattro incognite: φn , φt , x (t)
e ϑ (t). Le due equazioni differenziali sono del secondo ordine e richiedono due
condizioni iniziali per ogni funzione incognita. Si assumono le stesse utilizzate in
precedenza, in modo da poter confrontare i due casi:
⎧
x (0) = 0
⎪
⎪
⎨ ẋ (0) = v
0
ϑ (0) = 0
⎪
⎪
⎩
ϑ̇ (0) = vR0
8
Le funzioni x (t) e ϑ (t) soluzioni delle due equazioni differenziali sono le seguenti:
¢ 2
¡ g
½ 1
½
C
2
−
t +A t+B
ϑ
(t)
=
µ
ϑ̈
=
−C
+
µ
M
R
M
g
R
2
d
d
R
M
R
2
⇒
t2
ẍ = −µd g
x (t) = −µd g 2 + D t + E
Imponendo le condizioni iniziali:
⎧
x (0) = 0
⎪
⎪
½
2
⎨ ẋ (0) = v
ϑ (t) = − (C − µd M g R) Mt R2 +
0
⇒
2
ϑ (0) = 0
⎪
x (t) = −µd g t2 + v0 t
⎪
⎩
ϑ̇ (0) = vR0
v0
t
R
Il tempo di arresto td del baricentro G del disco è:
ẋ (t) = 0
⇒
ẋ (t) = −µd gt + v0 = 0 ⇒ td =
v0
µd g
e lo spazio di arresto:
Ld = x (td ) − x (0) =
1 v02
µd 2g
Si noti che un valore elevato della coppia C produce un arresto più rapido della
rotazione del disco, ma non influisce su Ld . L’istante t∗d in cui il disco smette di
ruotare è dato da:
ϑ̇ (t) = 0 ⇒ −2 (C − µd M g R)
t
v0
v0 M R
+
= 0 ⇒ t∗d =
2
M R
R
2 (C − µd M g R)
in cui il denominatore è positivo poiché C > Cmax e µs > µd . Ricavando C in
funzione di t∗d si ottiene:
¶
µ
3
v0
+ µd g M R > µs M g R = Cmax
C=
∗
2td
2
ovvero:
t∗d
v0
µd
<
=
3µs − 2µd µd g
¶
µ
µs − µd
td < td
1−3
3µs − 2µd
Dunque, il disco smette di ruotare prima che si arresti la sua traslazione.
Lo spazio minimo di arresto del moto di traslazione è dato da:
Lmin = min (Ls , Ld ) = Ls =
1 v02
1 v02
< Ld =
µs 2g
µd 2g
ed è quello associato al moto di puro rotolamento del disco. Per minimizzare
lo spazio di frenata è dunque necessario applicare al disco una coppia frenante
C = Cmax = 32 µs M g R, valore che dipende dal coefficiente di attrito statico µs .
Esercizio n.14
Un’asta pesante (AB) e una guida liscia semi-circolare sono poste in un piano
verticale. L’asta è vincolata a passare per l’estremità superiore della guida (D)
9
mediante un manicotto libero di ruotare, mentre l’estremo A scorre lungo la guida.
B
M, 4R
ϑ
F
G
p
D
R
A
La guida è di raggio R mentre l’asta è di lunghezza 4R e massa M. Nell’altro
estremo dell’asta (B) è applicata una forza verticale F costante nel tempo.
Nell’istante t = 0 l’asta è inclinata di π/4 rispetto ad un asse verticale (ϑ (0) = π/4)
ed è caratterizzata da velocità angolare nulla (ϑ̇ (0) = 0). Determinare il valore
minimo di F per cui il moto si attiva con rotazione in senso orario dell’asta.
− − − − − − − − − − − − − − −−
Si isola l’asta nella configurazione generica e si mettono in evidenza le forze ad essa
applicate, ovvero le reazioni vincolari φA e φD .
B
M, 4R
F
G
ϑ
D
p
φD
A
φA
R
C
Le reazioni vincolari opposte −φA e −φD , applicate sulla guida, non sono state
rappresentate nell’ultima figura sia per chiarezza grafica sia perché non verranno
utilizzate nella risoluzione dell’esercizio.
10
Il moto dell’asta è governato dalle solite due equazioni vettoriali della dinamica,
che si possono scrivere:
(
M aG = φA + φD + p + F
³−−−−→´
³−−−−→´
³−−−−→´
−
→
Γ̇ G = MG = A − G ∧ φA + D − G ∧ φD + B − G ∧ F
In esse compaiono le reazioni vincolari incognite φA e φD , reazioni che non sono
richieste dal problema. Si può allora considerare una equazione alternativa, ottenibile anche come combinazione lineare delle precedenti, che non coinvolge le
due reazioni incognite. Tale equazione è la seconda scritta in precedenza in cui si
sceglie il punto C come polo al posto del baricentro G.
³−−−−→´
³−−−−→´
−
→
Γ̇ C + vC ∧ (M vG ) = MC = G − C ∧ p + B − C ∧ F
In questo modo le reazioni vincolari, che hanno rette d’azione ortogonali alla guida
liscia, non danno contributo al momento. Si noti che C è anche il centro di istantanea rotazione dell’asta (teorema di Chasles: le velocità dei punti dell’asta in A e
D sono tangenti alla guida e dunque ortogonali ai segmenti AC e DC), ma essendo
vC e vG non paralleli occorre considerare il loro prodotto vettoriale come termine
aggiuntivo nell’equazione.
I vari termini della equazione possono essere calcolati considerando, ad esempio, il
sistema di riferimento cartesiano indicato nella figura seguente.
B
y, j
F
M, 4R
G
ϑ
p
D
φD
ϑ
ϑ
A
ϑ
φA
x, i
ϑ
k
R
C
⎧
³ ´
−
→
⎪
⎪
Γ
=
I
ϑ̇
−k
C
C
⎪
⎪
⎪
⎪
⎨ vG = ẋG i + ẏG j
vC = ẋC i + ẏC j
⎪
⎪
⎪
⎪
p = −M g j
⎪
⎪
⎩ F = −F j
11
Le coordinate di G, B e C si determinano da considerazioni trigonometriche:
⎧
GD = GA − AD = 2R − 2R cos ϑ = 2R (1 − cos ϑ)
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
xG = GD sin ϑ = 2R (1 − cos ϑ) sin ϑ
⎪
⎪
⎪
⎪
y = R + GD cos ϑ = R + 2R (1 − cos ϑ) cos ϑ
⎪
⎪
⎨ G
⎪
xB = BD sin ϑ = 2R (2 − cos ϑ) sin ϑ
⎪
⎪
⎪
⎪
yB = R + BD cos ϑ = R + 2R (2 − cos ϑ) cos ϑ
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
x = R sin 2ϑ
⎪
⎩ C
yC = R cos 2ϑ
Per il calcolo del momento d’inerzia IC occorre determinare la distanza GC:
2
2
2
GC = GD + DC = 4R2 (1 − cos ϑ)2 + (2R sin ϑ)2 = 8R2 (1 − cos ϑ)
µ
¶
7
1
2
2
2
2
− 2 cos ϑ
IC = IG + M GC = M (4R) + M 8R (1 − cos ϑ) = 4MR
12
3
Dunque si ha:
⎧ −
¢
¡
→
2 7
⎪
Γ
=
−4MR
−
2
cos
ϑ
ϑ̇ k
⎪
C
3
⎪
⎪
⎪
⎪
⎪
⎪
⎪
ẋG = 2R ϑ̇ (cos ϑ − cos 2ϑ)
⎪
⎪
⎪
⎪
⎪ ẏG = 2R ϑ̇ h(− sin ϑ + sin 2ϑ)
⎪
i
⎪
⎪
⎪
⎪
v
=
2R
ϑ̇
(cos
ϑ
−
cos
2ϑ)
i
+
(−
sin
ϑ
+
sin
2ϑ)
j
G
⎪
⎪
⎪
⎪
⎨
ẋC = 2R ϑ̇ cos 2ϑ
⎪
⎪
⎪
⎪
⎪ ẏC = −2R ϑ̇h sin 2ϑ
i
⎪
⎪
⎪
v
=
2R
ϑ̇
cos
(2ϑ)
i
−
sin
(2ϑ)
j
⎪
C
⎪
⎪
⎪
⎪
⎪
⎪
³−−−−→´
⎪
⎪
⎪
G − C = (xG − xC ) i + (yG − yC ) j = 2R (sin ϑ − sin 2ϑ) i + 2R (cos ϑ − cos 2ϑ) j
⎪
⎪
⎪
³−−−−→´
⎪
⎪
⎩ B − C = (xB − xC ) i + (yB − yC ) j = 2R (2 sin ϑ − sin 2ϑ) i + 2R (2 cos ϑ − cos 2ϑ) j
∙
µ
¶ ¸
−
→
7
2
2
Γ̇ C = −4MR 2ϑ̇ sin ϑ +
− 2 cos ϑ ϑ̈ k
3
2
vC ∧ (M vG ) = 4MR2 ϑ̇ sin ϑ k
³−−−−→´
G − C ∧ p = −2M g R (sin ϑ − sin 2ϑ) k
³−−−−→´
B − C ∧ F = −2F R (2 sin ϑ − sin 2ϑ) k
Inserendo i vari termini nell’equazione del moto e proiettando sul versore k si
ottiene l’equazione differenziale seguente:
µ
¶
7
2
2
4MR
− 2 cos ϑ ϑ̈+4MR2 ϑ̇ sin ϑ = 2M g R (sin ϑ − sin 2ϑ)+2F R (2 sin ϑ − sin 2ϑ)
3
12
Questa equazione è non-lineare e per essa non è possibile esprimere la soluzione ϑ (t)
mediante funzioni elementari. Però per rispondere al quesito iniziale è sufficiente
osservare che per la rotazione ϑ (t) si può scrivere lo sviluppo in serie di Maclaurin:
1
π 1
ϑ (t) = ϑ (0) + ϑ̇ (0) t + ϑ̈ (0) t2 + ... = + ϑ̈ (0) t2 + ...
2
4 2
Affinché l’asta proceda inizialmente in senso orario (ϑ (t) > π/4) è sufficiente che
risulti ϑ̈ (0) > 0. Dunque, dall’equazione del moto si ha:
2
M g (sin ϑ − sin 2ϑ) + F (2 sin ϑ − sin 2ϑ) − 2MR ϑ̇ sin ϑ
¡
¢
ϑ̈ (t) =
2MR 73 − 2 cos ϑ
M g
ϑ̈ (0) =
³
Risoluzione alternativa
´
¡√
¢
−1 +F
2−1
M g
¡7 √ ¢
>0 ⇒ F > √
2MR 3 − 2
2
√1
2
Essendo il sistema conservativo è possibile utilizzare il teorema di conservazione
dell’energia meccanica:
T − U = cost.
L’energia cinetica può essere calcolata come:
1
1
2
T = IG ϑ̇ + M |vG |2
2
2
oppure, essendo C il centro di istantanea rotazione dell’asta:
µ
¶
1
7
2
2
2
T = IC ϑ̇ = 2MR
− 2 cos ϑ ϑ̇
2
3
Per il potenziale delle forze si ha:
U = −M g yG −F yB = −M g [R + 2R (1 − cos ϑ) cos ϑ]−F [R + 2R (2 − cos ϑ) cos ϑ]
Nella configurazione iniziale (ϑ (0) = π/4) il sistema è in quiete (ϑ̇ (0) = 0); di
conseguenza si ottiene l’equazione del moto:
µ
¶
7
2
2
2MR
− 2 cos ϑ ϑ̇ + 2M g R (1 − cos ϑ) cos ϑ+
3
´
³ √
´
³√
2−1 +F R 2 2−1
+ 2F R (2 − cos ϑ) cos ϑ = M g R
In base alle considerazioni discusse nel paragrafo precedente occorre determinare
ϑ̈ (0). Derivando l’equazione del moto si ottiene:
¶ ¸
µ
∙
7
2
2
4MR ϑ̇ ϑ̇ sin ϑ +
− 2 cos ϑ ϑ̈ + 2M g R ϑ̇ (− sin ϑ + sin 2ϑ) +
3
+ 2F R ϑ̇ (−2 sin ϑ + sin 2ϑ) = 0
13
che risolta rispetto a ϑ̈ (t) fornisce:
2
M g (sin ϑ − sin 2ϑ) + F (2 sin ϑ − sin 2ϑ) − 2MR ϑ̇ sin ϑ
¡
¢
ϑ̈ (t) =
2MR 73 − 2 cos ϑ
ovvero, la stessa espressione ottenuta in precedenza. Da questa si ricava:
´
³
¡√
¢
1
√
−
1
+
F
2
−
1
M g
M g
2
¡7 √ ¢
>0 ⇒ F > √
ϑ̈ (0) =
2MR 3 − 2
2
Seconda risoluzione alternativa
Il teorema dell’energia cinetica afferma che:
Ṫ = Ṗe
con Ṗe potenza delle forze applicate all’asta
Ṗe = φA × vA + φD × vD + p × vG + F × vB
Essendo la guida liscia, le reazioni vincolari sono ortogonali alle velocità:
φA × vA = 0
φD × vD = 0
Gli altri due addendi possono essere determinati con riferimento al centro di istantanea rotazione C dell’asta:
i
→ ³−−−−→´ ³
−
→´ h
−
vG = ϑ̇ ∧ G − C = −ϑ̇ k ∧ 2R (sin ϑ − sin 2ϑ) i + 2R (cos ϑ − cos 2ϑ) j
i
→ ³−−−−→´ ³
−
→´ h
−
vB = ϑ̇ ∧ B − C = −ϑ̇ k ∧ 2R (2 sin ϑ − sin 2ϑ) i + 2R (2 cos ϑ − cos 2ϑ) j
semplificando:
h
i
vG = −2Rϑ̇ − (cos ϑ − cos 2ϑ) i + (sin ϑ − sin 2ϑ) j
h
i
vB = −2Rϑ̇ − (2 cos ϑ − cos 2ϑ) i + (2 sin ϑ − sin 2ϑ) j
e sostituendo nell’espressione della potenza si ottiene:
Ṗe = [2M g (sin ϑ − sin 2ϑ) + 2F (2 sin ϑ − sin 2ϑ)] ϑ̇ R
L’energia cinetica può essere scritta come:
T =
1
2
IC ϑ̇
2
e risulta sempre positiva (T (t) ≥ 0). Il sistema nella configurazione iniziale è in
quiete (T (0) = 0); ne consegue che, considerando lo sviluppo in serie di Maclaurin
per T :
T (t) = T (0) + Ṫ (0) t + ... = Ṫ (0) t + ...
14
per l’attivazione del moto è necessario che risulti:
Ṫ (0) > 0
ovvero, per il teorema dell’energia cinetica:
∙
µ
¶
µ
¶¸
1
1
Ṫ (0) = Ṗe (0) > 0 ⇒ 2M g √ − 1 + 2F 2 √ − 1
ϑ̇ (0) R > 0
2
2
Una rotazione inizialmente oraria corrisponde a ϑ̇ (0) > 0; ne consegue che dovrà
essere rispettata la disuguaglianza seguente:
µ
¶
µ
¶
1
1
M g
M g √ − 1 + F 2√ − 1 > 0 ⇒ F > √
2
2
2
Esercizio n.11 - seconda risoluzione alternativa
Il sistema è rappresentato dalla massa puntiforme mq , dal disco che rotola senza
strisciare sul piano inclinato e dal filo che scorre su un perno liscio.
s
ϑ
A
t
x
p
n
k
α
C
q
Esso è dunque conservativo e per scrivere l’equazione del moto si può utilizzare il
teorema di conservazione dell’energia meccanica:
T − U = cost.
in cui l’energia cinetica è:
1
1
1
2
T = IC ϑ̇ + mq ẋ2 =
2
2
2
µ
3
M R2
2
¶ µ
¶2
ẋ
1 q 2 3p + 8q 2
−
+
ẋ =
ẋ
2R
2g
16g
mentre il potenziale delle forze:
¡ ¢
U = p × s t + q x = p s sin α + q x
La relazione tra s e x si ricava osservando che:
⎧
vG = vG t
⎪
⎪
⎨
x
ẋ
vG = ṡ = R ϑ̇
⇒ ṡ = − ⇒ s = − + s0
⎪
v = vA t
2
2
⎪
⎩ A
vA = −ẋ = 2R ϑ̇
15
e il potenziale U , a meno di una inessenziale costante, risulta:
³
´
p
U = q − sin α x
2
L’equazione del moto è dunque la seguente:
´
p
3p + 8q 2 ³
ẋ − q − sin α x = cost.
16g
2
Derivando questa equazione rispetto al tempo si ottiene:
³
´
3p + 8q
p
2ẋẍ − q − sin α ẋ = 0
16g
2
che, essendo ẋ 6= 0, può essere semplificata nella seguente:
ẍ =
8q − 4p sin α
g
8q + 3p
espressione che coincide con quella trovata in precedenza.
In modo del tutto analogo l’esercizio poteva anche essere risolto utilizzando il
teorema dell’energia cinetica.
Esercizio n.15
Un disco di massa M e raggio r appartiene ad un piano verticale e inizialmente
rotola senza strisciare su una guida circolare di raggio R.
M, r
ϕ
G
C
ϑ
R
Assumendo che il disco sia inizialmente nell’estremità superiore della guida (ϑ (0) =
0) e che, in tale posizione, sia caratterizzato
da una velocità angolare positiva ma
p
di entità trascurabile (0 . ϕ̇ ¿ g/r), determinare il punto di distacco del disco
dalla guida nei due casi in cui:
(a) il vincolo tra disco e guida garantisca il perfetto rotolamento del primo fino
all’istante del distacco;
16
uρ
k
M, r
ϕ
G
φ
uϑ
p
C
ϑ ρ
R
O
Figure 1
(b) il vincolo tra disco e guida sia scabro con coefficiente d’attrito statico µs .
− − − − − − − − − − − − − − −−
Si isola il disco dalla guida e si mettono in evidenza le forze che agiscono sul
disco, cioè la reazione vincolare φ e il peso proprio p. Per la rappresentazione
del moto si utilizza un sistema di riferimento polare con i versori uρ e uϑ che
risultano, rispettivamente, normale e tangenziale alla guida nel punto C di contatto
col disco.Per il disco si possono scrivere le seguenti equazioni del moto:
(
M aG = φ + p
³−−−−→´
→
−
Γ̇ G = MG = C − G ∧ φ
con
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
φ = φn uρ + φt uϑ
p = (−p cos ϑ) uρ + (p sin ϑ) uϑ
³−−−−→´
G − O = (R + r) uρ
−−−→
→
−
d(G−O)
vG = dt = (R +hr) u̇ ρ = (R + r)
i ϑ̇ uϑ
2 −
→
⎪
dv
G
⎪
aG = dt = (R + r) −ϑ̇ u̇ ρ + ϑ̈ uϑ
⎪
⎪
⎪
⎪
⎪
⎪
⎪
³−−−−→´
⎪
⎪
⎪
C − G = −r uρ
⎪
⎪
⎪
³ ´
³ ´
⎪
⎪
⎩ ΓG = IG ϕ̇ −k = 1 MR2 ϕ̇ −k
2
17
Si sceglie di proiettare la prima equazione secondo i versori uρ e uϑ , in modo da
ottenere direttamente le componenti φn e φt della reazione vincolare; la seconda
viene proiettata secondo il versore k:
⎧
⎪
⎨ M aG × uρ = φ × uρ + p × uρ
M aG ³× uϑ´= φ × u³ϑ + p ×´uϑ
⎪
−−−→
⎩ I ϕ̈ −k × k = −
C −G ∧φ×k
G
Sostituendo le relazioni precedenti e semplificando si ottiene:
⎧
2
⎪
φn = p cos ϑ − ϑ̇ M (R + r)
⎪
⎪
⎪
⎨
φt = M (R + r) ϑ̈ − p sin ϑ
⎪
⎪
⎪
⎪
⎩ 1
− 2 Mr2 ϕ̈ = r φt
(1)
(a) Vincolo di puro rotolamento
Se il disco rotola senza strisciare sulla guida, il sistema è caratterizzato da un grado
di libertà e come coordinata libera si assume ϑ. L’angolo ϕ può essere determinato
come funzione di ϑ osservando che la velocità del punto di contatto C del disco è
nulla:
→ ³−−−−→´
−
vC = vG + ϕ̇ ∧ C − G = 0
³−−−−→´
Sostituendo le espressioni di vG e C − G ricavate in precedenza si ha:
i ³
´
h
(R + r) ϑ̇ uϑ + −ϕ̇k ∧ (−r uρ ) = 0
h
i
(R + r) ϑ̇ − r ϕ̇ uϑ = 0
h
i
R+r
ϑ̇
(R + r) ϑ̇ − r ϕ̇ = 0 ⇒ ϕ̇ =
r
Dal sistema di equazioni (1) si ottiene:
⎧
2
⎪
φn = p cos ϑ − ϑ̇ M (R + r)
⎪
⎪
⎪
⎨
(2)
φt = M (R + r) ϑ̈ − p sin ϑ
⎪
⎪
⎪
⎪
⎩
g
ϑ̈ = 23 R+r
sin ϑ
La terza equazione rappresenta l’equazione del moto ed è un’equazione differenziale
non lineare: per essa non è possibile esprimere la soluzione ϑ (t) mediante funzioni
elementari; è però possibile ricavare l’espressione della velocità angolare ϑ̇ (t) in
funzione della posizione ϑ (t) osservando che se si moltiplicano ambi i membri per
ϑ̇ (t) si ottengono due espressioni integrabili:
2 g
ϑ̈ ϑ̇ =
ϑ̇ sin ϑ
Z
Z3 R + r
2 g
ϑ̇ sin ϑ dτ + K
ϑ̈ ϑ̇ dτ =
3R+r
1 2
2 g
ϑ̇ = K −
cos ϑ
2
3R+r
18
La costante di integrazione K può essere determinata imponendo le condizioni
iniziali:
½
4 g
2
ϑ (t = 0) = 0
⇒ ϑ̇ =
(1 − cos ϑ)
(3)
ϑ̇ (t = 0) = 0
3R+r
Si noti che quest’ultima relazione rappresenta una equazione scalare del moto e,
poiché il sistema è conservativo, poteva essere ottenuta direttamente mediante il
teorema di conservazione dell’energia meccanica:
T − U = cost.
con:
¶ µ
µ
¶2
1
R+r
1 3
3
2
2
2
T = IC ϕ̇ =
Mr
ϑ̇ = M (R + r)2 ϑ̇
2
2 2
r
4
U = p [(R + r) − (R + r) cos ϑ]
da cui, imponendo le condizioni iniziali, si ottiene:
3
2
M (R + r)2 ϑ̇ = p (R + r) (1 − cos ϑ)
4
ovvero, semplificando, l’equazione (3).
Sostituendo l’espressione (3) nel sistema (2) si ottengono le componenti di reazione
φn e φt in funzione della posizione ϑ:
¡
¢
⎧
φn = 73 p cos ϑ − 47
⎪
⎪
⎪
⎨
φt = − p3 sin ϑ
⎪
⎪
⎪
⎩
g
ϑ̈ = 23 R+r
sin ϑ
Essendo il contatto tra disco e guida di tipo monolatero, il distacco avviene quando
la componente normale di reazione si annulla (φn = 0), ovvero per ϑ = ϑ̄:
µ ¶
4 ∼
ϑ̄ = arccos
= 0.9626 rad ∼
= 55◦ .15
7
(b) Vincolo scabro
Nel caso di vincolo scabro, il sistema è caratterizzato da un grado di libertà finché
c’è puro rotolamento (come coordinata libera si assume ϑ), mentre in presenza di
slittamento il sistema è caratterizzato da due gradi di libertà (come coordinate
libere si assumono ϑ e ϕ). La soluzione fornita nel paragrafo precedente (puro
rotolamento) vale finché è verificata la disuguaglianza di Coulomb:
|φt | < µs φn
Sostituendo le espressioni precedentemente determinate:
µ
¶
4
7
p
φn = p cos ϑ −
,
φt = − sin ϑ
3
7
3
19
si ricava:
∗
sin ϑ < (7 cos ϑ − 4) µs ⇒ ϑ = 2 arctan
Ã
3µs
p
1 + 33µ2s + 1
!
Se si rappresentano graficamente le due funzioni h (ϑ) = sin ϑ e f (ϑ) = (7 cos ϑ − 4) µs
si osserva immediatamente che ϑ∗ < ϑ̄, cioè il disco inizia a slittare prima del distacco, qualunque sia il valore del coefficiente d’attrito. Questo fatto consegue dalla
progressiva diminuzione della componente normale φn e dal corrispondente aumento di |φt | al crescere di ϑ (nella figura seguente è rappresentato il caso µs = 0.7
con ϑ∗ = 0.7752 rad ∼
= 44◦ .42).
2
f(ϑ)
h(ϑ)
1
ϑ
0.25
-1
0.5
0.75
*
ϑ
1
ϑ
1.25
1.5
-2
La velocità angolare del disco in corrispondenza di ϑ∗ = ϑ (t∗ ) è fornita dalla
relazione (3):
r
4 g
∗
∗
(1 − cos ϑ∗ )
ϑ̇ = ϑ̇ (t ) =
3R+r
r
4 R+r
R
+
r
(1 − cos ϑ∗ )
ϑ̇ (t∗ ) =
g
ϕ̇∗ = ϕ̇ (t∗ ) =
r
3
r2
Per ϑ > ϑ∗ (ovvero t > t∗ ) occorre analizzare il moto del disco in presenza dello
slittamento. Le equazioni governanti il moto sono rappresentate dal sistema (1) a
cui si aggiunge l’equazione di Coulomb; si noti che si hanno ancora tante equazioni
(4) quante sono le incognite (φn , φt , ϑ, ϕ):
⎧
2
⎪
φn = p cos ϑ − ϑ̇ M (R + r)
⎪
⎪
⎪
⎪
⎪
⎪
⎨ φt = M (R + r) ϑ̈ − p sin ϑ
(4)
⎪
1
2
⎪
⎪
− 2 Mr ϕ̈ = r φt
⎪
⎪
⎪
⎪
⎩
|φt | = µs φn ⇒ −φt = µs φn
20
Procedendo per sostituzione si ottiene:
⎧
2
⎪
φn = p cos ϑ − ϑ̇ M (R + r)
⎪
⎪
⎪
⎪
⎪
⎪
2
⎪
⎪
⎨ φt = −µs p cos ϑ + µs M (R + r) ϑ̇
h
i
2
⎪
µs
⎪
ϕ̈ = 2 r g cos ϑ − (R + r) ϑ̇
⎪
⎪
⎪
⎪
⎪
⎪
⎪
2
⎩
g
(sin ϑ − µs cos ϑ) + µs ϑ̇
ϑ̈ = R+r
La quarta equazione deve essere integrata numericamente utilizzando le condizioni
iniziali:
⎧
⎨ ϑ (t∗ ) = ϑ∗
⇒ ϑ = ϑ (t)
∗
⎩
ϑ̇ (t∗ ) = ϑ̇
Nota la funzione ϑ (t) si può tracciare φn (t) utilizzando
¡ ¢ la prima equazione del
sistema (4): il distacco avviene nell’istante t̂ in cui φn t̂ = 0; l’angolo di distacco
¡¢
è ϑ̂ = ϑ t̂ .
Per completare la soluzione si può procedere all’integrazione numerica della terza
equazione del sistema (4) con le seguenti condizioni iniziali:
⎧
ϑ (t∗ ) = R+r
ϑ∗
⎨ ϕ (t∗ ) = R+r
r
r
⇒ ϕ = ϕ (t)
∗
⎩
R+r
∗
ϑ̇
(t
ϑ̇
ϕ̇ (t∗ ) = R+r
)
=
r
r
Esercizio n.16
Un sistema è costituito da due dischi concentrici pesanti mutuamente vincolati
allo stesso perno liscio, in modo da poter ruotare liberamente, e da una molla
rotazionale relativa. I dischi hanno raggi R e r (R > r) e masse, rispettivamente,
M e m (M > m); la molla è di costante elastica K e di massa trascurabile. Il disco
di raggio R rotola senza strisciare su un piano orizzontale.
ϕ
M, R
ϑ
K
G
m, r
H
La definizione della rotazione relativa ϑ è tale per cui la molla non è sollecitata
(ovvero è "a riposo") per ϑ = 0.
21
Assumendo che nella configurazione iniziale (ϕ (0) = 0) il sistema sia in quiete
(ϕ̇ (0) = 0, ϑ̇ (0) = 0) e che la molla sia stata "caricata" assegnando un valore
ϑ (0) = π/2, determinare il moto del sistema. Trascure l’attrito volvente tra disco
e piano d’appoggio.
− − − − − − − − − − − − − − −−
Il sistema è caratterizzato da due gradi di libertà: come coordinate libere si scelgono
la rotazione assoluta ϕ del disco di raggio R e la rotazione relativa ϑ tra i due dischi.
Se si elimina la molla si possono mettere in evidenza le coppie (k ϑ) che questa
esercita sui due dischi: essendo la molla di massa trascurabile le coppie sono uguali
ed opposte.
ϕ
Kϑ
K
ϑ
M, R
Kϑ
G
Kϑ
Kϑ
m, r
φH
p +P
H
−φH
y, j
k
x, i
Per il sistema dei due dischi si possono scrivere le seguenti equazioni del moto:
(
(M + m) aG = φH + p + P
−
→
Γ̇ H + vH ∧ [(M + m) vG ] = MH
In particolare si noti che nella seconda il termine vH ∧[(M + m) vG ] risulta nullo se
si considera come punto H il punto geometrico di contatto sulla verticale di G, per
il quale vH = vG . Non si potrebbe invece considerare H come centro di istantanea
rotazione del sistema in quanto i due dischi sono soggetti a moti diversi e H è il
centro di istantanea rotazione del solo disco di raggio R, ma non del disco di raggio
r. Proiettando la prima equazione nelle direzioni dei versori i e j e la seconda in
22
direzione di k si ottiene:
⎧
³
´
⎪
⎪
(M
+
m)
a
×
i
=
φ
×
i
+
p
+
P
×i
G
H
⎪
⎨
³
´
con:
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
(M + m) aG × j = φH × j + p + P × j
⎪
⎪
→
⎪
⎩ −
Γ̇ H × k = MH × k
xG = R ϕ, ẋG = R ϕ̇, ẍG = R ϕ̈
yG = R, ẏG = 0, ÿG = 0
vG = ẋG i + ẏG j = R ϕ̇ i
aG = ẍG i + ÿG j = R ϕ̈ i
φH = φt i + φn j
p³ + P =´− (m + M) g j
−−−−→
H − G = −R j
³−−−−→´ ³
´
MH = H − G ∧ p + P + Kϑ k − Kϑ k = 0
Il momento della quantità di moto dei due dischi rispetto a H può essere calcolato
come somma dei momenti di ciascun disco:
i
h
³−−−−→´
r
R
r
ΓH = ΓR
+
Γ
=
Γ
+
Γ
+
G
−
H
∧
mv
G =
H
H
H
G
³
´ ³ ´i
³ ´ h³−−−−→´
R
= IH
ϕ̇ −k + G − H ∧ mvG + IGr ϕ̇ + ϑ̇ −k
³ ´ 3
³ ´
R
R
2
ΓH = IH ϕ̇ −k = M R ϕ̇ −k
2
³
´ ³ ´ 1
³
´³ ´
r
r
2
−k = m r ϕ̇ + ϑ̇ −k
ΓG = IG ϕ̇ + ϑ̇
³
´ ³
´ 2
³ ´
³−−−−→´
G − H ∧ mvG = R j ∧ m R ϕ̇ i = mR2 ϕ̇ −k
∙
¸³ ´
³
´
3
1
2
2
2
ϕ̇ + ϑ̇ + m R ϕ̇ −k
ΓH = M R ϕ̇ + m r
2
2
Il sistema di equazioni governanti il moto si riduce al seguente:
⎧
⎪
φt = (M + m) R ϕ̈
⎪
⎪
⎪
⎨ φn = (m + M) g
→
−
Γ̇ H × kh = 0 ⇒ ΓH × k =³cost. ´⇒
⎪
i
⎪
⎪
⎪
⎩ ⇒ − 3 M R2 ϕ̇ + 1 m r2 ϕ̇ + ϑ̇ + m R2 ϕ̇ = cost.
2
2
in cui la costante di integrazione si ricava imponendo le condizioni iniziali:
½
³
´
1
3
ϕ̇ (t = 0) = 0
M R2 ϕ̇ + m r2 ϕ̇ + ϑ̇ + m R2 ϕ̇ = 0
⇒
ϑ̇ (t = 0) = 0
2
2
(5)
Le equazioni del moto si completano con quelle relative al solo disco di raggio r o,
in alternativa, con quelle relative al solo disco di raggio R. Isolando, ad esempio,
23
il disco di raggio r occorrerebbe mettere in evidenza la reazione vincolare φG che il
perno esercita sul disco: questa ha come punto di applicazione il baricentro G del
disco e, di conseguenza, se si scrive l’equazione della derivata del momento della
quantità di moto rispetto a G tale reazione non compare:
µ−
´r
→ ¶r ³
Γ̇ G = MG
(6)
con
⎧ ³ ´r
³
´ ³ ´
³
´³ ´
⎨ ΓG = IGr ϕ̇ + ϑ̇
−k = 12 m r2 ϕ̇ + ϑ̇ −k
³
´r ³ −−−→´
³−−−−→´
⎩ MG = −
G − G ∧ φG + G − G ∧ p + Kϑ k = Kϑ k
Proiettando tale relazione su k si ottiene:
³
´
1
m r2 ϕ̈ + ϑ̈ = −Kϑ
2
(7)
Il sistema di equazioni differenziali lineari (5) e (7) può essere risolto per sostituzione: derivando (5) e sostituendo ϕ̈ in (7) si ottiene un’equazione differenziale
lineare in ϑ del secondo ordine:
µ
¶
1
m r2
2
−
mr
ϑ̈ + ϑ̈ = −Kϑ
2
3M R2 + m r2 + 2m R2
ovvero:
K 3M R2 + m r2 + 2m R2
m r2
3M R2 + 2m R2
La soluzione dell’equazione è ben nota ed è:
ϑ̈ + λ2 ϑ = 0,
con: λ2 = 2
(8)
ϑ (t) = A1 cos (λt) + A2 sin (λt)
e le costanti di integrazione A1 e A2 si determinano imponendo le condizioni iniziali:
½
½
½
ϑ (0) = π2
A1 = π4
A1 cos (0) + A2 sin (0) = π4
⇒
⇒
−A1 λ sin (0) + A2 λ cos (0) = 0
A2 = 0
ϑ̇ (0) = 0
π
cos (λt)
2
Sostituendo questa funzione nell’equazione (7) si ha:
¶
µ
2K π
2
ϕ̈ = λ −
cos (λt)
m r2 2
ϑ (t) =
Integrando e imponendo le condizioni al contorno si ottiene l’espressione di ϕ (t):
µ
¶
π
2K
2
ϕ (t) = − λ −
cos (λt) + A3 t + A4
2
mr
2λ2
m r2
π
cos (λt) + A3 t + A4
ϕ (t) = −
2
2
2
3M R + m r + 2m R 2
½
½
m r2
π
ϕ (0) = 0
A4 = 3M R2 +m
r2 +2m R2 2
⇒
ϕ̇ (0) = 0
A3 = 0
24
π
m r2
[1 − cos (λt)]
2
2
2
3M R + m r + 2m R 2
Il moto del sistema è quindi rappresentato dai due dischi che oscillano periodicamente con una frequenza f = λ/ (2π) che dipende dai parametri geometrici (r e
R), di massa (M e m) e dalla rigidezza della molla K.
Si noti che il moto è illimitato nel tempo, ovvero l’energia inizialmente fornita alla
molla si conserva trasformandosi periodicamente da elastica a cinetica: il sistema è
conservativo. Questo fatto, che poteva essere osservato fin dall’inizio, permette di
utilizzare il teorema di conservazione dell’energia meccanica al posto di una delle
equazioni del moto, ad esempio in sostituzione della (6):
ϕ (t) =
T − U = cost.
con
¸
∙
´2 1
1 R 2
1 r ³
2
T = IH ϕ̇ +
ϕ̇ + ϑ̇ + m (R ϕ̇) =
I
2
2 G
2
³
´
2
1
1
3
= M R2 ϕ̇2 + m r2 ϕ̇ + ϑ̇ + m R2 ϕ̇2
4
4
2
1
U = − K ϑ2
2
³
´2 1
3
1
1
M R2 ϕ̇2 + m r2 ϕ̇ + ϑ̇ + m R2 ϕ̇2 + K ϑ2 = cost.
4
4
2
2
equazione che derivata fornisce la seguente:
³
´³
´
3
1
M R2 ϕ̇ϕ̈ + m r2 ϕ̇ + ϑ̇ ϕ̈ + ϑ̈ + m R2 ϕ̇ϕ̈ + K ϑϑ̇ = 0
2
2
Dall’equazione (5) si ricava:
3MR2 + 2mR2 + m r2
ϕ̇
m r2
m r2
ϑ̈
ϕ̈ = −
3MR2 + 2mR2 + m r2
ϑ̇ = −
Sostituendo queste espressioni nella precedente e semplificando ci si conduce all’equazione
in ϑ (ottenuta senza utilizzare la (6)):
ϑ̈ + 2
che coincide con la (8).
K 3MR2 + m r2 + 2mR2
ϑ=0
m r2
3MR2 + 2mR2