La propagazione della luce in una fibra ottica
La rifrazione della luce
Consideriamo due mezzi trasparenti alla luce, separati da una superficie piana. Il primo
mezzo ha indice di rifrazione n1, il secondo n2, con n2<n1. Ciò significa che la velocità v di
propagazione della luce è più grande nel mezzo 2 che nel mezzo 1, perché in generale
v = c / n, dove c = 3·108 m/s e n è l’indice di rifrazione del mezzo.
Superficie di
separazione
Mezzo 2,
con indice n2<n1
Mezzo 1,
con indice n1
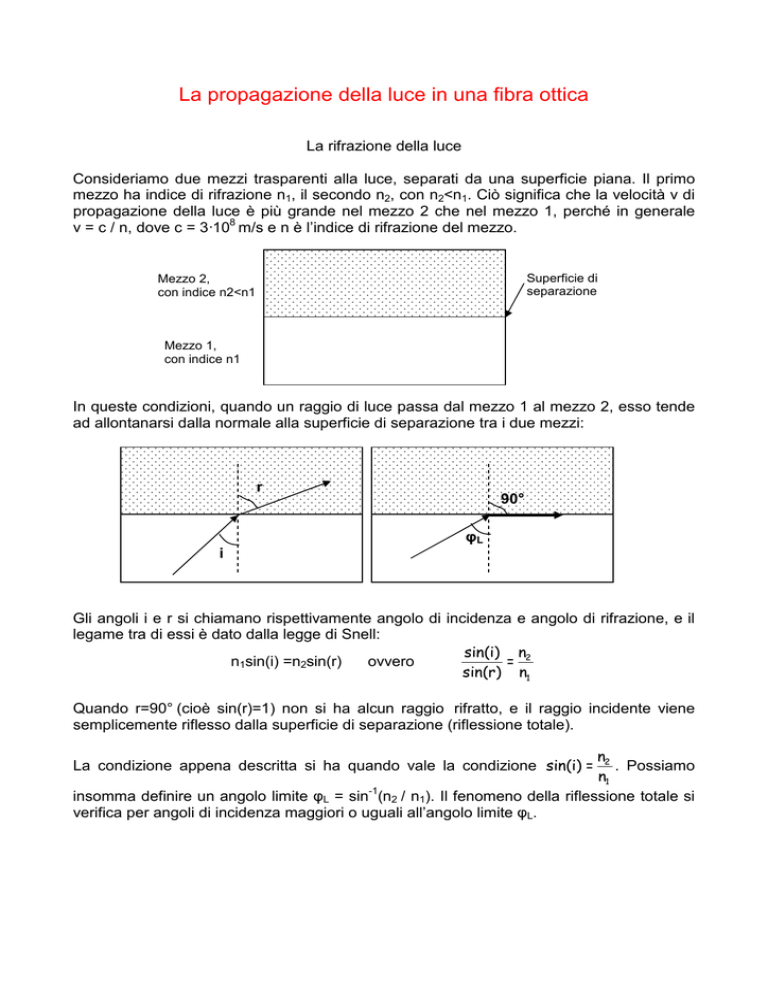
In queste condizioni, quando un raggio di luce passa dal mezzo 1 al mezzo 2, esso tende
ad allontanarsi dalla normale alla superficie di separazione tra i due mezzi:
r
90°
φL
i
Gli angoli i e r si chiamano rispettivamente angolo di incidenza e angolo di rifrazione, e il
legame tra di essi è dato dalla legge di Snell:
sin(i) n2
ovvero
=
n1sin(i) =n2sin(r)
sin(r) n1
Quando r=90° (cioè sin(r)=1) non si ha alcun raggio rifratto, e il raggio incidente viene
semplicemente riflesso dalla superficie di separazione (riflessione totale).
n2
. Possiamo
n1
insomma definire un angolo limite φL = sin-1(n2 / n1). Il fenomeno della riflessione totale si
verifica per angoli di incidenza maggiori o uguali all’angolo limite φL.
La condizione appena descritta si ha quando vale la condizione sin(i) =
Le fibre ottiche a salto di indice
La costituzione di una fibra ottica a salto di indice è mostrata nella figura che segue:
nucleo e mantello sono naturalmente trasparenti alla luce, mentre la guaina protettiva è
opaca.
Guaina protettiva, plastica nera
Mantello, polimero con indice n2
n2
Nucleo, polimero con indice n1
n1
2 mm
mantello
Guaina protettiva, plastica nera
Dato che il mantello ha indice di rifrazione inferiore rispetto al nucleo, si può verificare il
fenomeno della riflessione totale. Quindi, per angoli di ingresso sufficientemente piccoli, un
raggio di luce continua a propagarsi nel nucleo.
Angolo di accettazione e apertura numerica
Perché il raggio incida con angolo limite φL sulla superficie di separazione tra nucleo e
mantello, occorre che esso incida sulla superficie di separazione tra aria e nucleo con un
opportuno angolo φM, che si chiama angolo di accettazione.
Mantello, n2
φL
Aria, n0 = 1
90°- φL
Nucleo, n1
φM
Si ha:
sin(ϕ M )
n
= 1 , dove n0 = 1 se il mezzo da cui proviene il raggio è l’aria.
sin(90°-ϕ L ) n0
Avremo perciò:
sin(ϕ M ) = n1sin(90°-ϕ L ) = n1 cos(ϕ L ) = n1 1 − sin2 (ϕ L )
Come abbiamo visto, sin(φL) = n2 / n1, e quindi:
sin(ϕ M ) = n1 1 −
n22
= n12 − n22
n12
A quest’ultima grandezza si dà il nome di apertura numerica della fibra.
La dispersione modale
Consideriamo un impulso luminoso che si propaga lungo la fibra. I percorsi di
propagazione seguiti dai raggi di luce sono diversi, perciò sono diversi anche i rispettivi
tempi di percorrenza.
Se la fibra ha lunghezza L, il tempo di percorrenza minimo si avrà per il raggio che viaggia
in direzione dell’asse:
L
n
tm = = L 1
v
c
Il tempo massimo si avrà per il raggio con incidenza pari all’angolo limite:
L
n1 L n12
tM =
⋅ = ⋅
sinϕ L c n2 c
La dispersione modale è, per definizione, la differenza tra i due tempi:
L n1
⋅ ⋅ (n1 − n2 )
c n2
La prossima figura mostra come la dispersione modale abbia anche l’effetto di allargare la
forma dell’impulso luminoso immesso all’ingresso
∆t = tM − tm =
(tmin + tmax)/2
Impulso
all’ingresso
Impulso
all’uscita
tmin
Modo 1
(lungo l’asse)
tmax
Modo 2
(incidenza pari
all’angolo limite)
Misura della velocità della luce in una fibra ottica
L’esperimento consiste nell’inviare impulsi brevi di luce (di durata inferiore a 50 ns) in una
fibra ottica al termine della quale è posto un fotodiodo che trasforma il segnale luminoso in
uno elettrico.
Osservando questo segnale con un oscilloscopio di normali caratteristiche, si può
confrontare il tempo impiegato dall’impulso luminoso a percorrere uno spezzone di fibra
ottica molto corto (circa 20 cm) con quello impiegato a percorrerne uno molto più lungo
(20.14 m). Dalla differenza dei tempi si può calcolare la velocità della luce nel mezzo di cui
è composta la fibra ottica.
Schema a blocchi del dispositivo
Risultati di una misura
A titolo di esempio, in un esperimento da noi eseguito si sono ottenuti i seguenti risultati:
∆t1
∆t2
A
A
B
B
Spezzone di fibra ottica da 20 cm
Spezzone di fibra ottica da 20 m
Segnali visualizzati sull’oscilloscopio
∆t1 = 46 ns ± 4 ns
∆t2 = 148 ns ± 4 ns
∆t = 102 ns ± 8 ns
20.14 m
m
v=
= 1.97 ⋅ 108
102ns
s
Il risultato è in accettabile accordo con i dati relativi all’indice di rifrazione della fibra ottica
per la luce rossa usata nell’esperimento: n = 1.492.
Nota 1: potendosi ritenere trascurabile il tempo impiegato dalla luce a percorrere 20 cm,
l’intervallo ∆t1 rappresenta sostanzialmente i tempi di risposta del LED emettitore e del
fotodiodo ricevitore.
Nota 2: la sensibilità dell’asse dei tempi dell’oscilloscopio usato è di 4 ns, controllata con
un oscillatore al quarzo.
Nota 3: la sensibilità verticale richiesta per il canale A è di 50 mV, per il canale B di 1 mV.
Le sonde usate devono essere di tipo compensato in frequenza, per non alterare la forma
del segnale da visualizzare. Esse però riducono il segnale di un fattore 10.
Nota 4: nel calcolo si è trascurato l’effetto della dispersione modale, che come si vedrà
risulta di circa 3 ns.
Schema elettrico del ricevitore di impulsi luminosi
La capacità parassita C è costituita dalla capacità parassita della sonda (dell’ordine di
qualche pF), da quella del fotodiodo (12 pF nominali) e dalla circuiteria: pertanto C può
essere valutata in 15 pF massimo.
Ne consegue che, per evidenziare impulsi dell’ordine delle decine di ns, la resistenza R
deve essere:
50 ns
R<
3300 Ω
15 pF
La resistenza effettiva R è il risultato di un compromesso tra questa condizione e
l’ampiezza del segnale da visualizzare sull’oscilloscopio.
Schema a blocchi del generatore di impulsi luminosi
Schema elettrico del circuito di alimentazione
Schema elettrico del clock a f = 30 kHz
f =
1
t1 = 0.693(RA + RB ) ⋅ C
t 2 = 0.693R B ⋅C
t1 + t2
RA = 1200 Ω
RB = 22000 Ω
C = 1 nF
Schema elettrico del monostabile
τ ≈ 0.7 RC ≈ 50 ns
CM = 27 pF
RM si regola agendo sul trimmer da 20 kΩ
Schema elettrico dell’amplificatore di potenza
Al canale A
dell’oscilloscopio, per
visualizzare l’impulso di
corrente che attraversa il
LED emettitore
RS = 1000 Ω
C = 1 nF
D è un diodo Schottky