Induzione
elettrica
Conduttori e condensatori
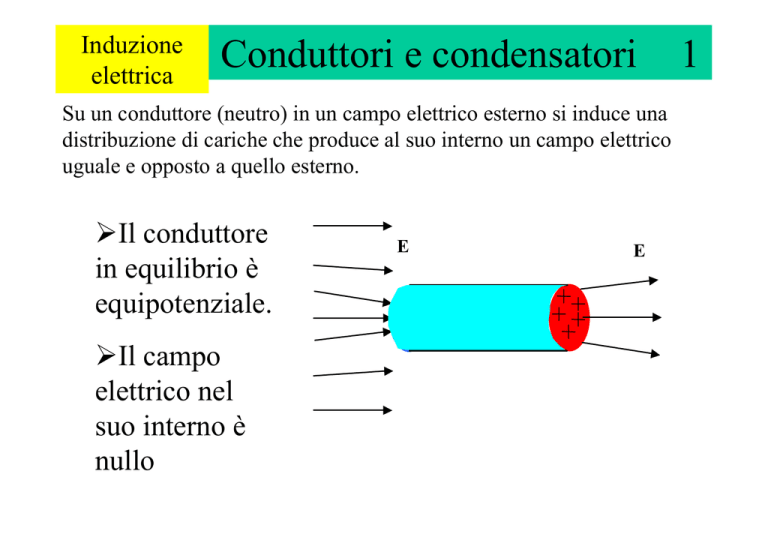
Su un conduttore (neutro) in un campo elettrico esterno si induce una
distribuzione di cariche che produce al suo interno un campo elettrico
uguale e opposto a quello esterno.
¾Il conduttore
in equilibrio è
equipotenziale.
¾Il campo
elettrico nel
suo interno è
nullo
E
E
E-+E+
1
Conduttore
carico
Conduttori e condensatori
2
In una sfera conduttrice carica deformata il campo interno è sempre nullo
⇒ la densità di carica superficiale nei punti più distanti dal centro è
maggiore che in quelli vicini.
La densità di
carica
superficiale è
inversamente
proporzionale
al quadrato
del raggio di
curvatura
E = En =
E
σ
εo
E
Schermo
elettrico
Conduttori e condensatori
3
Il campo prodotto all'esterno dipende dalla distribuzione di cariche alla
superficie dello schermo conduttore, che è determinata unicamente dal
requisito di annullamento del campo prodotto all'interno.
Le forze prodotte
da un campo
esterno agiscono
sullo schermo ma
non sulle cariche
distribuite al suo
interno.
La distribuzione delle cariche interne non muta il campo esterno;
viceversa, il campo esterno non influenza le cariche interne (schermo
di Faraday, descritto già da Benjamin Franklin nel 1755)
“messa a
terra”
Conduttori e condensatori
La "messa a terra" dello schermo annulla la risultante delle forze
elettriche sullo schermo.
¾La "messa a terra" dello schermo
elimina anche le azioni di forza dei
campi esterni sullo schermo.
¾L'effetto di schermatura consente
di verificare con enorme precisione
(1/1016) la legge di Coulomb-Gauss.
Terra
4
La sfera
carica
Conduttori e condensatori
5
Il potenziale della sfera (R)
carica (Q) è
¾ = al lavoro di E da R a ∞
¾ = al potenziale di una carica
Q nel centro per r≥R
∞
Q
Q
V (Q, R) = ∫ k e 2 dr = k e
R
r
R
E = ke
Q
r2
L’energia
della sfera
Conduttori e condensatori
V(q)
Lavoro per
aumentare di dq la
carica q sulla sfera =
V
dq
V(q)dq
Lavoro complessivo
per portare una
carica Q sulla sfera
=
energia Ec della
sfera carica
q
0
Q
Q
0
0
E C = ∫ V (q )dq = ∫
Q
q dq
1 Q2
=
4πε 0 R 2 4πε 0 R
6
Capacità
della sfera
Conduttori e condensatori
La capacità C della sfera è il rapporto tra la carica Q e il potenziale V
C≡
Q
V
La capacità si misura in farad (F)
coulomb(C)
farad(F) =
volt(V)
Capacità della Terra (raggio R ≈ 6300 km)
R
C=
= 4πε 0 R ≈ 7(10 − 4 )F
ke
7
Condensatore
e capacità
Conduttori e condensatori
La sfera conduttrice carica, assieme al conduttore idealmente
all'infinito con carica di segno opposto, costituisce un condensatore.
La capacità del condensatore si determina in linea di principio
¾ calcolando il campo elettrico prodotto dalle
cariche +Q e –Q sulle armature
¾ calcolando il lavoro di E da una armatura
all'altra (ossia il potenziale V del
condensatore)
8
Gusci
concentrici
Conduttori e condensatori
9
Esempio: calcolo di C per gusci sferici concentrici con R1 <R2
R2
1
R2 − R1
1
V ≡ ∫ E (r )dr = keQ − = keQ
R1R2
R1 R2
R1
E(r)
Q
E (r ) = ke 2
r
r
R1
R2
C=
R1 R2
Q
=
V k e (R2 − R1 )
2 →∞
R
→ C = R1 / k e = 4πε 0 R1
2
4
π
R
1
2 − R2 = d << R1
R
→ C = ε 0
d
condensatore
Conduttori
piano
e condensatori
10
Condensatore a facce piane (S) e parallele (distanti d)
Eint = E1 + E2 = 2
σ
Q
=
2ε 0 ε 0 S
Eext = 0
E2
E1
−σ2
Qd
V = E ⋅d =
ε0S
C=
Q
S
= ε0
V
d
1 Q 2 1 Q 2d 1
2
(S ⋅ d )
EC =
=
= ε 0 Eint
2 C 2 ε 0S 2
E2
d
E1
σ1
E2
E1
Densità di
energia
Conduttori e condensatori
11
Per il condensatore piano l’energia è proporzionale al volume
interno e al quadrato del campo elettrico (uniforme) all’interno del
condensatore
1 Q 2 1 Q 2d 1
2
(S ⋅ d )
EC =
=
= ε 0 Eint
2 C 2 ε 0S 2
L’energia del
condensatore risiede
energia dEC
nel campo elettrico tra
= 3
volume dr
le armature. Il campo
densità di EC =
elettrico ha una densità
di energia
EC 1
2
E
=
ε
0
proporzionale al
Sd 2
quadrato di E
Condensatori
Conduttori
in parallelo
Q1
C1 =
V
Q1
Q2
C2 =
V
Q2
e condensatori
Q1 + Q2
C=
V
V ⇔ V
C1 parallelo C2 ≡ C1 + C2
Q1 + Q2
12
Condensatori
Conduttori
in serie
Q
C1 =
V1
V1
Q
C2 =
V2
V2
e condensatori
Q
C=
V1 + V2
⇔
1
1
C1 serie C2 ≡
+
C1 C2
−1
C1C2
=
C1 + C2
13
Esempio di
calcolo
Conduttori e condensatori
14
Nel calcolo della capacità del condensatore occorre sommare la
superficie S delle armature di polarità opposta tra loro affacciate
S
a
b
c
3C
Sε o
C=
d
a
b
c
2C
d












