Parte A
del 12.12.2003
obbligatorio - iscrizione sulla lista
Esame di:Calcolo delle probabilità - studenti IOL docente: E.Piazza
Una risp osta a ciascuno dei 10 test qui assegnati è considerata valida se e soltanto se tutti i valori di verità relativi sono stati indicati
correttamente.
Cognome
Nome
matr.n.
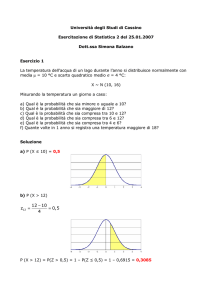
1) Sia X una variabile aleatoria continua, distribuita uniformemente su [0, 1]. Allora:
Figura 1:
V
F
F
il grafico in (a) è quello della densità di
X
il grafico in (b) è quello della densità di −X
il grafico in (c) è quello della densità di 2X
2) Siano A e B due generici eventi che verificano B ⊂ A e P (A) = p, P (B) = (1 − p) ( 12 < p < 1); indicare
quale delle seguenti risposte è vera:
V
P [AB] = 1 − p
V
P [AB] ≤ p
F
P [AB] = P [A]P [B]
√
F
P [AB] ≥ p
F
P [B|A] = 0
3) Un insieme contenente M elementi bianchi e N elementi neri ha esattamente:
¡M ¢
F
N sottoinsiemi
V
2M+N sottoinsiemi
F
(M + N )2 sottoinsiemi
4) Un laboratorio ha un test che individua il 99% delle volte un virus quando questo è presente e ne segnala la
presenza l’1% delle volte quando il virus non c’è. Se il 5% della popolazione ha questo virus qual è la probabilità
che Tizio risultato positivo al test abbia davvero il virus?
Indicare con D = {Tizio ha il virus}, E = {Tizio risulta positiva al test}
Soluzione:
P [E|D]P [D]
0.99 · 0.05
P [D|E] =
=
= 0.83898
P [E|D]P [D] + P [E|Dc ]P [Dc ]
0.99 · 0.05 + 0.01 · 0.95
5) Sia X una variabile aleatoria ∼ N (0, 1) e Φ la sua funzione di ripartizione. Allora:
V
F
F
F
V
P [|X| > 2.5] = 2[1 − Φ(2.5)]
P [|X| > 2.5] = Φ(2.5) − Φ(−2.5)
P [|X| > 2.5] = è circa 1
P [|X| > 2.5] = 1 − Φ(2.5)
α = P [X ≤ Φ−1 (α)]
6) Supponiamo di estrarre un campione casuale di dimensione 90 da una popolazione X che sappiamo con
certezza essere distribuita secondo una legge normale di media 0 e varianza ignota. Supponiamo che i valori
di X campionati siano stati divisi in classi di frequenza centrate nei numeri interi e che tali classi presentino i
seguenti valori di frequenze assolute osservate:
osservazione
freq.assolute
-5
18
-3
3
0
18
6
3
8
3
11
3
20
6
23
36
che sono distribuite secondo il seguente grafico:
Figura 2:
6.1) Calcolare
media
10.2667
varianza dei dati 145.529
moda
23
0,3 quantile
0
6.2)
F
se la minima osservazione fosse -10 invece di -5 la moda cambierebbe
F
se la massima osservazione fosse 35 invece di 23 la mediana cambierebbe
V
se
½ la minima osservazione fosse -10 invece di -5 la media cambierebbe
se lasciamo invariate tutte le frequenze assolute osservate tranne quelle dei valori
F
-3 e 20, che diventano rispettivamente 6 e 3, lo 0.3 quantile cambierebbe
7) Sia Φ(x) la funzione di ripartizione di una va normale X di media 0 e varianza 1 e sia a > 0. Allora:
V
F
V
F
V
P [X ≤ −a] = 1 − Φ(a)
P [|X| ≤ a] = 2Φ(a)
P [|X| ≥ a] = 2 − 2Φ(a)
1
P [|X| ≥ 0] =
2
x = P [X ≤ Φ−1 (x)]
8) Quale/quali delle seguenti funzioni è una densità di probabilità?
F
V
F
F
V
−e−x , x√∈ (−∞, +∞)
λ
√
e−λ x I(0,∞) (x)
2 x
−2I(−1/2,0) (x)
λe−λx I(0,3) (x)
2I(−1/2,0) (x)
9) Si consideri il quadrato Q di lato r su cui è assegnata una distribuzione di probabilità uniforme (P [Q] = 1),
e il sottoinsieme S di Q rappresentato dal settore circolare indicato in figura con centro in A e raggio r.
Figura 3:
Si scelga a caso un punto nel quadrato. Calcolare la probabilità P [S] che il punto appartenga a S.
P [S] =
area(S)
π
=
area(Q)
4
1
10) Sia X una va la cui fd ammette fgm data da: (e2t + 1).
2
10.1 Trovare media e varianza
di X.
¯
¯
¯
¯
¯
¯
d 1 2t
d2 1
µX = E[X] =
= e2t ¯t=0 = 1; σ 2X = 2 (e2t + 1)¯¯
− 1 = 2e2t ¯t=0 − 1 = 1.
(e + 1)¯¯
dt 2
dt 2
t=0
t=0
1
10.2 Sia Y una bernoulliana di parametro p = . Applicando la definizione, calcolare la funzione generatrice
2
di momenti di 2Y e verificare MOTIVANDO, che è la fgm data.
1 1
1
La va 2Y prende i valori 0 e 2 ciascuno con probabilità . Perciò E[et2Y ] = + e2t
2
2 2
Parte B
1. Un’azienda possiede una macchina dedicata alla produzione di un unico tipo di transistor. Sia X la
variabile aleatoria (va) che codifica con “1 il transistor generico prodotto quando è difettoso (e con “0” quando
non lo è) e sia p = P [X = 1], 0 ≤ p ≤ 1.
1.1 Scrivere la legge di probabilità f (x, p) di X
p = P [X = 1]; 1 − p = P [X = 0]; X va di Bernulli di media p.
La legge di probabilità di X è data da:
f (x, p) = P [X = x] = px (1 − p)1−x ; x = {0, 1}.
I transistor vengono prodotti uno dopo l’altro, in successione. Siamo all’inizio di un giorno di lavoro qualsiasi.
La macchina viene avviata e inizia a produrre. Si supponga che, mediamente, la macchina produca transistor
difettosi in una percentuale pari al 6%. Sia W la va che conta i transistor non difettosi prodotti prima di averne
uno difettoso.
1.2 Scrivere la funzione di densità discreta (fdd) fW (m) di W e calcolare, in termini di valori di W, la
probabilità dell’evento A½= {il primo transistor prodotto dalla macchina è difettoso}.
pq m m = 0, 1, 2, . . .
P [W = m] = fW (m) =
, distribuzione geometrica. Segue che P [A] = P [W = 0] = 0.06
0
altrove
1.3 Calcolare, in termini di valori di W, la probabilità dell’evento B = {il primo transistor difettoso prodotto
è il centesimo}
P [B] = P [W = 99] = (0.94)99 0.06
1.4 Calcolare il tempo medio d’attesa (in termini di transistor prodotti) che precede il primo transistor
difettoso.
Si tratta di calcolare la media E[W ] di W. È noto che, se p è la probabilità di produrre un transistor difettoso
1−p
allora la va W ha media data da E[W ] =
= 0.94
0.06 = 15.667. da cui...
p
1.5 Calcolare la probabilità che avendo prodotto 20 transitor di fila difettosi, il 21-esimo sia ancora difettoso.
W è la va che conta i transistor difettosi prodotti prima di un transistor non difettoso. W ha distribuzione
geometrica di parametro 0.94. Per W vale la proprietà di assenza di memoria, cioè P [W ≥ k + n | W ≥ k] =
P [W ≥ n]. Nel nostro caso k = 20, n = 1. P [W ≥ 1] = 1 − P [W = 0] = 0.94, cioè la stessa probabilità di avere
un transitor non difettoso prodotto al primo colpo.
Supponiamo ora che la durata di uno di questi transitor sia ben modellata da una variabile aleatoria X
misurata in migliaia di ore che ha distribuzione esponenziale di media pari a 40000 ore (attenzione: l’unità di
misura di X è migliaia di ore).
1.6 Scrivere, CON PRECISIONE, la funzione di densità fX (x) e la funzione di ripartizione FX (x) di X.
1
X ∼ Exp(λ) e poiché E[X] = 40 si deduce che λ =
= 0.025 da cui si ha:
40
1
1 −1x
fX (x) =
e 40 I[0,+∞) (x) = 0.025e−0.025x I[0,+∞) (x) e FX (x) = (1−e− 40 x )I[0,+∞) (x) = (1−e−0.025x )I[0,+∞) (x)
40
1.7 Disegnare CON PRECISIONE il grafico di fX (x)
Figura 4:
Supponiamo ora che l’azienda, oltre ai transistor di vita media paria a 40000 ore, ne produca anche di qualità
1
della vita media di quelli di buona qualità). Sia ancora
più scadente cioè con vita media pari a 4000 ore (
10
X la va che misura (in migliaia di ore, ricordate?) la durata dei transistor di buona qualità mentre sia S la va
che misura la durata dei transistor di qualità scadente (sempre in migliaia di ore).
Supponiamo che il 76% dei chip sia di buona qualità e il 24% sia di qualità scadente.
1.8 Qual è la probabilità che un transitor scelto a caso dalla produzione sia di buona qualità?
0.76
1.9 Calcolare la probabilità che un transitor di qualità scadente duri più di 2500 ore, cioè P [S >?].
1
P [S > 2.5] = e− 4 2.5
1.10 Si scelga un transistor a caso dalla produzione. Calcolare la probabilità che funzioni ancora dopo 1000
ore (Suggerimento: indicare con A = {il transitor scelto funziona ancora dopo 1000 ore}; con B = {il transitor
è di buona qualità}; con B c = {il transitor è di qualità scadente}).
1
1
P [A] = P [A | B]P [B] + P [A | B c ]P [B c ] = P [T > 1] · 0.76 + P [S > 1] · 0.24 = 0.76e− 40 + 0.24e− 4 = 0.92815
1.11 Per evitare di spedire troppi transitor difettosi alla clientela ogni transitor viene testato dalla azienda
per 1000 ore. Calcolare la probabilità che il transitor spedito sia di buona qualità sapendo che il transitor
funziona ancora dopo 1000 ore (cioè P [B | A]).
Per il teorema di Bayes si ha:
1
P [A | B]P [B]
0.76e− 40
P [B | A] =
=
1
1 = 0.79862 =
P [A]
0.76e− 40 + 0.24e− 4
1.12 Perché l’azienda puo testare i transitor per un po’ di ore e poi venderli come nuovi?
Perché, se la durata del transitor è ben modellata da una va esponenziale, il transistor non è soggetto a
usura (mancanza di memoria della esponenziale).
2. Un sistema di comunicazione accetta in input un voltaggio positivo v e in output un voltaggio misurato
da una va Y = αv + X dove X è una va normale di media µ = 0 e varianza σ 2 = 4 e α = 0.1.
2.1 Calcolare (usando la tavola in fondo al testo) il valore che deve avere v affinché P [Y < 0] = 0.015
N (αv; 4) − αv
0.1v
0.1v
Y ∼ N (αv; 4) ⇒ P [Y < 0] = P [
<−
] = 0.015 ⇒ −
= −2.17 ⇒ v = 21.7
2
2
2
2.2 Come si distribuisce la va W = −X? Disegnare il grafico della funzione di densità della W (indicando
CON PRECISIONE il valore del massimo, le ascisse degli eventuali punti di flesso, eccetera).
Per la simmetria di N è W ∼ N (0, 4)
I grafici delle funzioni di densità e di ripartizione di W coincidono con quelli della N (0, 4).
Figura 5:
2.3 Calcolare la probabilità dell’evento {|W | > 2}
P [|W | > 2] = P [|N (0; 1)| > 1] = 2 − 2Φ(1) = 2 − 2 · 0.8413 = 0.3174
Figura 6:
x
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
3.1
3.2
3.3
3.4
P
P [X ≤ x]
P [X ≤ −x]
P [|X| ≤ x]
P [|X| ≥ x]
.00
5000
5398
5793
6179
6554
6915
7257
7580
7881
8159
8413
8643
8849
9032
9192
9332
9452
9554
9641
9713
9772
9821
9861
9893
9918
9938
9953
9965
9974
9981
9987
9990
9993
9995
9997
.01
5040
5438
5832
6217
6591
6950
7291
7611
7910
8186
8438
8665
8869
9049
9207
9345
9463
9564
9649
9719
9778
9826
9864
9896
9920
9940
9955
9966
9975
9982
9987
9991
9993
9995
9997
.02
5080
5478
5871
6255
6628
6985
7324
7642
7939
8212
8461
8686
8888
9066
9222
9357
9474
9573
9656
9726
9783
9830
9868
9898
9922
9941
9956
9967
9976
9982
9987
9991
9994
9995
9997
3.5
999865
4.0
x
Φ(x)
Φ(−x)
2Φ(x) − 1
2 − 2Φ(x)
1.282
.9
.1
.8
.2
.03
5120
5517
5910
6293
6664
7019
7357
7673
7967
8238
8485
8708
8907
9082
9236
9370
9484
9582
9664
9732
9788
9834
9871
9901
9925
9943
9957
9968
9977
9983
9988
9991
9994
9996
9997
.04
5160
5557
5948
6331
6700
7054
7389
7704
7995
8264
8508
8729
8925
9099
9251
9382
9495
9591
9671
9738
9793
9838
9875
9904
9927
9945
9959
9969
9977
9984
9988
9992
9994
9996
9997
9999683
1.645
.95
.05
.9
.1
1.960
.975
.025
.95
.05
4.5
.05
5199
5596
5987
6368
6736
7088
7422
7734
8023
8289
8531
8749
8944
9115
9265
9394
9505
9599
9678
9744
9798
9842
9878
9906
9929
9946
9960
9970
9978
9984
9989
9992
9994
9996
9997
.06
5239
5636
6026
6406
6772
7123
7454
7764
8051
8315
8554
8770
8962
9131
9279
9406
9515
9608
9686
9750
9803
9846
9881
9909
9931
9948
9961
9971
9979
9985
9989
9992
9994
9996
9997
9999966
2.326
.99
.01
.98
.02
2.576
.995
.005
.99
.01
.07
5279
5675
6064
6443
6808
7157
7486
7794
8078
8340
8577
8790
8980
9147
9292
9418
9525
9616
9693
9756
9808
9850
9884
9911
9932
9949
9962
9972
9979
9985
9989
9992
9995
9996
9997
5.0
.08
5319
5714
6103
6480
6844
7190
7517
7823
8106
8365
8599
8810
8997
9162
9306
9429
9535
9625
9699
9761
9812
9854
9887
9913
9934
9951
9963
9973
9980
9986
9990
9993
9995
9996
9997
.09
5359
5753
6141
6517
6879
7224
7549
7852
8133
8389
8621
8830
9015
9177
9319
9441
9545
9633
9706
9767
9817
9857
9890
9916
9936
9952
9964
9974
9981
9986
9990
9993
9995
9997
9998
99999971
3.090
.999
.001
.998
.002
3.291
.9995
.0005
.999
.001
3.891
.99995
.00005
.9999
.0001
4.417
.999995
.000005
1
0
c Lo svolgimento del presente elaborato è coperto da diritto d’autore. Pertanto esso non può essere sfruttato a fini commerciali
°
o di pubblicazione editoriale. Ogni abuso sarà perseguito a termini di legge dal titolare del diritto.