CIRCUITI 2
segnali AC sinusoidali
misura di ampiezze e fasi
risposta in frequenza del multimetro
misura di impedenze
Laboratorio di Fisica
Dipartimento di Fisica G.Occhialini
Università di Milano Bicocca
PARTE PRIMA: Comportamento di una resistenza per segnali sinusoidali, risposta dei multimetri
Obiettivo: 1. verificare che iniettando un segnale sinusoidale in una resistenza il segnale in uscita è una sinusoide con la stessa frequenza e la stessa fase. 2. valutare la banda di “true RMS” dei multimetri (cioè l'intervallo di frequenza su cui effettuano misure corrette). 3. valutare impedenza e sfasamento tensione­corrente per una resistenza e per una capacità.
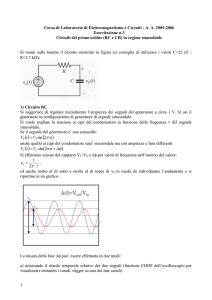
Procedimento: si costruisce il circuito come in figura dove Z è la resistenza di cui si studierà il comportamento in regime sinusoidale e di cui si misurerà l'impedenza (leggendo la tensione ai suoi capi e la corrente che la attraversa). La resistenza R è introdotta nel cicuito per poter leggere la corrente anche con l'oscilloscopio (in quanto questo strumento misura solo tensioni, la corrente è ricavata come rapporto VR/R) e il suo valore è assunto noto (lo si misuri con il multimetro). Si usa un generatore di funzioni per produrre un segnale sinusoidale in ingresso al circuito della forma (ddp rispetto alla massa):
V(t) = V0 sin(ωt+φ) = V0 sin(2πν t+φ)
di cui verrà fatta variare la frequenza (si studi p.es. l'intervallo 60 Hz­100 kHz) mentre la tensione V0 verrà mantenuta costante durante tutto l'esperimento (si imposti una tensione sufficientemente alta per ridurre gli effetti di rumore, p.es. 5­10 V). Si utilizza l'oscilloscopio per verificare che il segnale letto sia in A che in B è di forma sinusoidale con la stessa frequenza del segnale di ingresso: VA(t)=VA sin(ωt+φΑ) VB(t)=VB sin(ωt+φΒ)
Si ricava la differenza di potenziale ai capi di Z valutando V A(t)­VB(t) mediante la funzione “MATH” dell'oscilloscopio. verifica inoltre che la fase dei due segnali è identica (cioè la resistenza non introduce uno sfasamento), perciò la ddp tra A e B è pari a VA­VB
A questo punto si usano sia i multimetri che l'oscilloscopio per misurare l'ampiezza del segnale. L'amperometro ed il voltmetro devono trovarsi nella modalità AC, in cui misurano il valore RMS (valore efficace) della tensione: VRMS=V0/√2 (o analogamente della corrente). I multimetri forniscono una lettura corretta del segnale solo su una banda limitata di frequenze. Per avere una lettura sempre corretta di tensione e corrente si utilizza l'oscilloscopio. Con l'oscilloscopio si misuri:
l'ampiezza VA del segnale VA(t)
l'ampiezza VB del segnale VB(t) l'ampiezza VB­A del segnale differenza VA(t)­VB(t)1
la corrente che circola nel circuito, VB(t)/R
la differenza di fase ∆φ tra il segnale di tensione ai capi di Z (cioè VA(t)­VB(t)) ed il segnale di corrente IB=VB(t)/R
la differenza di fase ∆φ ' tra VA(t) e VB(t)
Si raccolgano dati in una tabella al variare della frequenza facendo attenzione a riportare (o convertire opportunamente) grandezze controntabili tra loro (tensione RMS o tensione picco­picco o ampiezza) e valutando per ciascun dato l'errore associato. Si ripeta la misura sostituendo alla resistenza Z una capacità (si effettuino in questo caso le misure unicamente con l'oscilloscopio).
ν
Vmultimetro Imultimetro
VA
VB
∆φ ' VB­A
∆φ
Ι Β =V B /R
Table 1: Dati da raccogliere (le letture con i multimetri solo per Z=resistenza). Analisi dei dati:
1. Banda passante dei multimetri: si confrontino i valori di tensione e corrente letti da multimetro ed oscilloscopio costruendo un grafico (attenzione a confrontare sempre valutazioni omologhe: RMS, picco­picco, ampiezze):
Vmultimetro (ω) / VB­A (ω) Imultimetro (ω) / IB (ω) (si usi una scala logaritmica per le frequenze). Cosa si osserva ? (si svolga questo punto solo nel caso in cui Z è una resistenza).
1 si noti che in generale dati due segnali sinusoidali aventi la stessa frequenza ma differente fase: VA(t)=V0 sin(ωt+φΑ) VB(t)=VB sin(ωt+φΒ) VA(t)­VB(t) sarà un segnale sinusoidale con la stessa frequenza ed un'ampiezza VB­A in generale diversa dalla differenza tra le ampiezze dei due segnali di partenza. Infatti, VB­A = VA­VB solo se le fasi dei segnali di partenza sono uguale. 2. Modulo dell'impedenza Z: si valuti il modulo dell'impedenza Z in funzione della frequenza come rapporto tra ampiezza del segnale di tensione e ampiezza del segnale di corrente:
|Z(ω)| = VB­A / I
e lo si riporti in grafico. Si fitti il grafico per valutare R o C (ricordando che nel caso della capacità |Z(ω)| = 1/(ωC))
3. Fase impedenza Z: si valuti lo sfamento tensione­corrente ai capi della capacità costruendo il grafico ∆φ (ω)
4. Funzione di trasferimento: (si svolga questo punto solo nel caso in cui Z è una capacità) si valutino le funzione di trasferimento del circuito nel caso di lettura del segnale di uscita su Z o su R. La funzione di trasferimento valuta l'ampiezza del segnale di uscita rispetto al segnale di ingresso e la sua fase. Il segnale di uscita può essere prelevato su Z o su R, quindi si possono identificare due funzioni di trasferimento definite in questo modo: lettura su Z |H(ω)| = VB­A / VA
arg [H(ω)}] = ∆φ
lettura su R |H(ω)| = VB / VA
arg [H(ω)}] = ∆φ '
Si riportino gli andamenti in un grafico (su scala bilogaritmica per |H(ω)|), si provi ad estrarre il valore di C da un fit della funzione di trasferimento. Note:
−
−
−
−
che ruolo gioca la resistenza interna del generatore di funzioni ? è importante conoscere il suo valore ?
verificare che il riferimento di massa utilizzato per oscilloscopio, generatore di funzioni e circuito sia lo stesso (come si fa?);
scegliere se riportare in grafico la pulsazione o la frequenza (soprattutto indicare sempre sul grafico quale delle due grandezze si è rappresentata);
si scelga la resistenza R in modo che sia molto più piccola della resistenza interna di voltmetro e oscilloscopio (che è ~ 1 MΩ), per la capacità C si scelga un valore molto maggiore della capacità di ingresso dell'oscilloscopio (che è ~ 20 pFarad)
Richiami sugli strumenti:
­ Il generatore di funzioni è uno strumento capace di produrre un segnale di forma variabile, nel caso di questa esperienza si utilizza un segnale sinusoidale. Il generatore ha un'impedenza interna Rg (usualmente di 50 Ohm) e il segnale di uscita viene dato su un connettore coassiale. Il segnale è quindi prelevato tra il pin centrale e l'armatura esterna del connettore coassiale. L'armatura esterna è la massa di riferimento dello strumento (generalmente messa a massa sulla terra dell'impianto elettrico del laboratorio).
­ L'oscilloscopio è uno strumento in grado di leggere e visualizzare una forma d'onda variabile nel tempo. La banda bassante dell'oscilloscopio (cioè la massima frequenza alla quale la lettura dell'oscilloscopio è ancora affidabile) è molto ampia (>60 Mhz per gli oscilloscopi di questo laboratorio). Gli oscilloscopi che abbiamo in laboratorio hanno un'impedenza di ingresso alta (~ 1 MOhm) posta in parallelo ad una capacità (~20 pF). I segnali vengono letti mediante un connettore coassiale come ddp tra il pin centrale e la massa (armatura esterna del connettore), questo cavo ha una capacità di 100 pF/m. A frequenze inferiori alla sua banda l'oscilloscopio fornisce una lettura corretta del segnale, a patto che questo sia prelevato dal circuito mediante una connessione che non alteri il segnale stesso. Per questo conviene utilizzare le sonde.
oscilloscopio
circuito
da testare
cavo BNC
di collegamento
ROSC COSC
Ccavo
La sonda di un oscilloscopio nella modalità x1 funziona come un semplice sistema di collegamento elettrico resistivo tra oscilloscopio e circuito da testare. Nella modalità x10 (sonda compensata) essa introduce ha un effetto di attenuazione del segnale (di cui l'oscilloscopio può automaticamente tenere conto se si seleziona la modalità sonda x10) e consente di evitare eventuali deformazioni del segnale ad opera del cavo di collegamento.