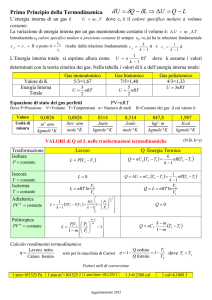
Primo principio della termodinamica
Consideriamo un contenitore isolato termicamente su cui vi è dell’acqua nella quale è immerso un
frullatore.
Questo, una volta messo in azione, compie lavoro sul liquido e quindi trasferisce parte della sua
energia alle molecole del liquido aumentando la sua energia interna dallo stato U1 allo stato U2.
Possiamo quindi scrivere:
U 2 U1 L
Ora consideriamo lo stesso sistema nella condizione U2 e poniamolo a riscaldare in un altro
contenitore (che sarà anch’esso isolato termicamente tranne la parte inferire che viene riscaldata).
Posto sotto riscaldamento il sistema aumenta la sua temperatura e quindi di conseguenza la sua
energia interna e passa dalla stato U2 a quello di U3.
Scriviamo la relazione:
U3 U 2 Q
Sommiamo ora membro a membro:
U 3 U1 U Q L
Per convenzione il lavoro fatto sul sistema prende sempre valore negativo, mentre quello fatto dal
sistema positivo; e il calore assorbito viene considerato come positivo mentre quello ceduto me
negativo.
Di conseguenza essendo nel nostro caso L minore di zero e Q maggiore di zero la nostra equazione
può essere semplificata e quindi generalizzata nella seguente (che vale per ogni situazione, mentre
la precedente solo per le simili a quella analizzata):
U Q L
questo è chiamato il primo principio della termodinamica, che può essere visto come un enunciato
della conservazione dell’energia.
In generale è molto utile calcolare il lavoro fatto o subito dal sistema e il calore emesso o assorbito
durante le trasformazioni termodinamiche di gas perfetti.
Poiché durante una trasformazione qualunque non si può calcolare il lavoro ed il calore in quanto
generalmente il sistema non passa da situazioni di equilibrio e quindi sarebbe impossibile applicare
il calcolo differenziale e poi integrale a delle variazioni che non seguono un andamento regolare
(cioè esprimibile con una equazione), per praticità si fa riferimento a certe trasformazioni che
vengono condotte passando da posizioni successive di equilibrio cioè realizzate dalla somme di
tutte le variazioni infinitesimali del sistema.
Queste trasformazioni si dicono reversibili o quasi-statiche.
Queste, essendo definite in ogni loro momento, possono essere rappresentate in un diagramma in
cui un punto è caratterizzato dalle tre variabili macroscopiche: la temperatura, la pressione e il
volume.
Siccome un diagramma tridimensionale è piuttosto complicato da seguire si è scelto di
rappresentare solo due variabili: la pressione e il volume.
Questi diagrammi prendono quindi il nome di diagrammi PV.
Da tener presente che ad ogni punto corrisponde anche un valore della temperatura, calcolabile
mediante la relazione PV=nRT.
Inoltre in tali diagrammi è spesso utile rappresentare dei rami di iperbole definite dall’equazione
P=nRT/V (con nRT=costante) chiamate isoterme, in cui è chiaro che ogni punto ha lo stesso valore
di temperatura dato che la massa del gas rimane costante.
Vi sono quattro tipi di trasformazioni che sono degne di una particolare attenzione: le isocore, le
isobare, le isoterme e le adiabatiche.
Trasformazione isocora_
Una trasformazione isocora è una trasformazione in cui variano la pressione e la temperatura,
mentre rimane costante il volume.
Nel diagramma PV è rappresentata da un segmento parallelo all’asse delle ordinate.
Il lavoro risulta essere nullo siccome non vi è nessuno
spostamento.
Il calore pertanto risulta essere pari alla variazione di
temperatura; e da ciò è possibile ricavare il calore specifico a
volume costante dei gas perfetti (per semplicità si
considererà prima un gas monoatomico).
U Q
3
da cui
ncv T nRT
Q ncv T
2
3
U nRT
2
e quindi
cv
3
R
2
Per un gas biatomico il calore specifico a volume costante è pari a 5/2R e per un gas triatomico a
7/2R.
Trasformazione isobara_
Una trasformazione isobara è una trasformazione in cui variano il volume e la temperatura, mentre
rimane costante la pressione.
Nel diagramma PV è rappresentata da un segmento parallelo all’asse delle ascisse.
In questo caso, essendo la pressione costante, il lavoro risulta
che L=P∆V, infatti L=F∆s=(F/A)*A∆s=P∆V.
Nel grafico corrisponde all’area grigia.
Il calore scambiato è
Q U L
da cui
Q ncv T PV
nRTV
poi si ha che Q ncv T
V
Q n(cv R)T
infine
ed essendo la trasformazione a pressione costante possiamo dire che il calore specifico a pressione
costante è:
c p cv R
Trasformazione isoterma_
Una trasformazione isoterma è una trasformazione in cui variano il volume e la pressione, mentre
rimane costante la temperatura.
Nel diagramma PV è rappresentata da un ramo di iperbole equilatera avente per asintoti gli assi P e
V, per cui questo tipo di trasformazione si muove lungo le
isoterme di cui abbiamo parlato precedentemente.
Siccome la temperatura rimane costante la variazione di energia interna risulta essere nulla e di
conseguenza il lavoro sarà pari al calore scambiato:
Per calcolare il lavoro in funzione della variazione di volume, siccome la pressione non rimane
Q
L
costante, occorre differenziare P∆V dopo aver
espresso
P in funzione della temperatura che è
costante e poi integrare il tutto; non riporterò la dimostrazione basti sapere che:
L nRT ln
V2
V1
Trasformazione adiabatica_
Una trasformazione isoterma è una trasformazione in cui variano tutte e tre le variabili
macroscopiche, però ha la particolarità di avvenire in condizioni che
impediscono lo scambio di calore.
In queste trasformazioni la variazione di energia interna è pari al
lavoro, e per questo anche se viene condotta una adiabatica
irreversibile è comunque possibile calcolarne il lavoro, infatti
l’energia interna è una variabile di statocioè
dipende
U che
Q
ncV Tsolo dallo
stato finale e iniziale.
In questo genere di trasformazioni si può dimostrare differenziando
l’equazione di stato dei gas perfetti, applicando poi un artificio
matematico ed infine integrando che:
PV const
dove γ=cp/cv; abbiamo quindi che γ sarà un numero sicuramente positivo e maggiore di zero e
pertanto l’andamento della trasformazione sarà simile a quella dell’isoterma ma tenderà più
velocemente ad intersecare l’ascissa (ovviamente senza mai incontrarla).