M - NON SOLO PROF.

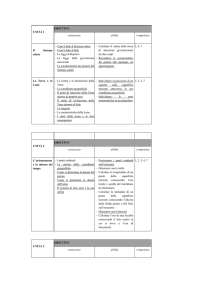
IL QUADRATO
Caratteristiche
Aˆ  Bˆ  Cˆ  Dˆ  90
Aˆ  Bˆ  Cˆ  Dˆ  360
AB  BC  CD  AD lato (l)
AC  BD diagonale (d)
Ciascuna diagonale divide il quadrato in due triangoli
rettangoli uguali i cui cateti corrispondono ai lati del
quadrato e l’ipotenusa alla diagonale del quadrato
IL RETTANGOLO
2p  4 l
2p
l
4
A  l2
l A
FORMULE
formula diretta per calcolare il perimetro conoscendo il lato
formula inversa per calcolare il lato conoscendo il perimetro
formula diretta per calcolare l’Area conoscendo il lato
formula inversa per calcolare il lato conoscendo l’Area
POSSIAMO CONSIDERARE IL QUADRATO COME UN ROMBO per cui la sua area può essere calcolata così
d2
formula diretta per calcolare l’area conoscendo la diagonale
2
d  2 A formula inversa per calcolare la diagonale conoscendo l’Area
A
Grazie al teorema di Pitagora:
d  l  2 formula per calcolare la diagonale conoscendo il lato
d
formula per calcolare il lato conoscendo la diagonale
l
2
(ricorda che
2  1,414... )
FORMULE
2 p  2  b  h  formula diretta per calcolare il perimetro conoscendo la base e l’altezza, cioè le due dimensioni
p  b  h  formula diretta per calcolare il semiperimetro conoscendo la base e l’altezza. Utile nei problemi in cui
mi viene data una relazione fra le due dimensioni e mi serve la loro somma
Caratteristiche
Aˆ  Bˆ  Cˆ  Dˆ  90
Aˆ  Bˆ  Cˆ  Dˆ  360
AB  CD
AD  BC
AC  BD
base (b)
altezza (h)
diagonale (d)
Ciascuna diagonale divide il rettangolo in due triangoli
rettangoli uguali i cui cateti corrispondono alla base e
all’altezza del rettangolo e l’ipotenusa alla diagonale del
rettangolo
A  b  h formula diretta per calcolare Area conoscendo la base e l’altezza
A
b  formula inversa per calcolare la base conoscendo l’Area e l’altezza
h
A
h  formula inversa per calcolare l’altezza conoscendo l’Area e la base
b
PARALLELOGRAMMA
FORMULE
POSSIAMO CONSIDERARE IL PARALLELOGRAMMA COME LA DEFORMAZIONE RIGIDA DI UN RETTANGOLO
2 p  2  l1  l2  Formula diretta per calcolare il perimetro conoscendo i due lati diversi del parallelogramma
p  l1  l2  Formula diretta per calcolare il semiperimetro conoscendo i due lati diversi. Utile nei problemi in cui
A  bh
H
Caratteristiche
Aˆ  Bˆ  Cˆ  Dˆ  360
Aˆ  Cˆ e Dˆ  Bˆ
Aˆ , Dˆ e Bˆ , Cˆ coppie di angoli supplementari
mi viene data una relazione fra le due dimensioni e mi serve la loro somma
formula diretta per calcolare l’area conoscendo la base e l’altezza. ATTENZIONE: è indifferente
considerare come base un lato o l’altro del parallelogramma. E’ però fondamentale, scelto il lato che si
userà come base, scegliere l’altezza ad esso relativa!!!! Quindi se considero come base
sarà
A
h
A
h
b
b
AB  CD lato1, AD  BC lato2, AD // BC e
AB // CD
AH Altezza rel. alla base CD , AK altezza rel. alla base BC
AC e BD diagonali di diversa lunghezza e si tagliano nel
CD , L’altezza
AH , mentre se considero come base BC , l’altezza sarà AK .
formula inversa per calcolare la base conoscendo l’Area e l’altezza
formula inversa per calcolare l’altezza conoscendo l’Area e la base
loro punto medio E).
ROMBO
FORMULE
POSSIAMO CONSIDEARE IL ROMBO COME LA DEFORMAZIONE RIGIDA DI UN QUADRATO
Caratteristiche
Aˆ  Bˆ  Cˆ  Dˆ  360 - Aˆ  Cˆ e Dˆ  Bˆ
Aˆ , Dˆ e Bˆ , Cˆ coppie di angoli supplementari
-
AB  BC  CD  AD lato (l) . AH altezza relativa
alla base BC .
AC e BD diagonali di diversa lunghezza e si tagliano
nel loro punto medio O e sono
incontrandosi formano 4 angoli retti).
perpendicolari,
AC e BD sono anche bisettrici degli angoli da cui hanno
origine
2 p  4  l formula diretta per calcolare il perimetro conoscendo il lato
2p
formula inversa per calcolare il lato conoscendo il perimetro
l
4
d  dM
Formula diretta per calcolare Area conoscendo la diagonale minore d m e la maggiore d M
A m
2
2A
formula inversa per calcolare la d m conoscendo l’area e la d M
dm 
dM
2A
dM 
formula inversa per calcolare la d M conoscendo l’area e la d m
dm
Possiamo guardare il rombo anche come parallelogrammo quindi il lato diventa base ed il segmento
altezza. Allora:
A  l h
dove
AH diventa
l è uno dei quattro lati uguali ed h è la sua altezza relativa che corrisponde al segmento AH
TRAPEZIO ISOSCELE
2 p  2l  bm  bM Formula diretta per calcolare il perimetro conoscendo i lati
b  bM   h formula diretta per calcolare l’Area conoscendo le due basi e l’altezza
A m
2
2A
formula inversa per calcolare l’altezza conoscendo l’Area e le due basi
h
bm  bM 
bm  bM   2 A formula inversa per calcolare la somma delle basi conoscendo l’Area e l’altezza
h
H
Caratteristiche
Aˆ  Bˆ  Cˆ  Dˆ  360
Aˆ  Bˆ e Dˆ  Cˆ ; Aˆ , Dˆ e Bˆ , Cˆ
AD  BC lati obliqui uguali l 
FORMULE
coppie di angoli suppl.
DC // AB basi del trapezio, DC  bm base minore
AB  bM
NB: non esiste una formula che mi permetta di calcolare subito le singole basi; posso arrivare alla loro somma con
la formula precedente e poi il problema mi deve fornire altre relazioni fra le due basi per cui si debba utilizzare la
loro somma.
AH  KB 
bM
base maggiore
 bm 
2
DH  CK Altezze h, AC  DB diagonali del trapezio
AH  KB proiezioni dei lati obliqui sulla base maggiore
TRAPEZIO SCALENO
Caratteristiche
H
K
Aˆ  Bˆ  Cˆ  Dˆ  360
Aˆ  Bˆ  Cˆ  Dˆ ; Aˆ , Dˆ e Bˆ , Cˆ coppie angoli supplementari
AD  BC i lati obliqui sono diversi  AD  l1 , BC  l2
DC // AB basi del trapezio, DC  bm base minore
AB  bM
base maggiore
DH  CK altezze h, AH  KB proiezioni dei lati obliqui
sulla bM
AC  DB
diagonali del trapezio
formula per calcolare una delle due proiezioni dei lati obliqui sulla base maggiore
FORMULE
2 p  l1  l2  bm  bM Formula diretta per calcolare il perimetro conoscendo i lati
b  bM   h formula diretta per calcolare l’Area conoscendo le due basi e l’altezza
A m
2
2A
formula inversa per calcolare l’altezza conoscendo l’Area e le due basi
h
bm  bM 
bm  bM   2 A formula inversa per calcolare la somma delle basi conoscendo l’Area e l’altezza
h
NB: non esiste una formula che mi permetta di calcolare subito le singole basi; posso arrivare alla loro somma con
la formula precedente e poi il problema mi deve fornire altre relazioni fra le due basi per cui si debba utilizzare la
loro somma.
AH  KB 
bM
 bm 
2
formula per calcolare una delle due proiezioni dei lati obliqui sulla base maggiore
TRAPEZIO RETTANGOLO
2 p  h  l2  bm  bM Formula diretta per calcolare il perimetro conoscendo i lati
b  bM   h formula diretta per calcolare l’Area conoscendo le due basi e l’altezza
A m
2
2A
formula inversa per calcolare l’altezza conoscendo l’Area e le due basi
h
bm  bM 
bm  bM   2 A formula inversa per calcolare la somma delle basi conoscendo l’Area e l’altezza
h
H
Caratteristiche
Aˆ  Bˆ  Cˆ  Dˆ  360
Aˆ  Dˆ  90 e Bˆ  Cˆ ;
Aˆ , Dˆ e Bˆ , Cˆ coppie di angoli suppl.
NB: non esiste una formula che mi permetta di calcolare subito le singole basi; posso arrivare alla loro somma con
la formula precedente e poi il problema mi deve fornire altre relazioni fra le due basi per cui si debba utilizzare la
loro somma.
DC // AB basi del trapezio, DC  bm base minore
AB  bM
FORMULE
BH  bM  bm 
formula per calcolare la proiezione del lato obliquo sulla base maggiore
base maggiore
DA  CH Altezze h, AC  DB diagonali del trapezio
BH proiezione dell’unico lato obliquo sulla base maggiore
TRIANGOLO ISOSCELE
H
Caratteristiche
Aˆ  Bˆ  Cˆ  180
Aˆ  Bˆ angoli alla base
AB  BC (lato l)
CH  AB  CHA, CHB triangoli rettangoli uguali
AH  HB perché l’altezza è anche mediana della base
ACˆ H  BCˆ H l’altezza è bisettrice dell’angolo al vertice
FORMULE
2 p  b  2l formula diretta per calcolare il perimetro conoscendo la base e i lati obliqui
bh
formula diretta per calcolare l’area conoscendo la base e l’altezza
A
2
2A
formula inversa per calcolare la base conoscendo l’Area e l’altezza
b
h
2A
formula inversa per calcolare l’altezza conoscendo l’Area e la base
h
b
FORMULA DI ERONE (per calcolare Area conoscendo solo i lati)
2 p  perimetro  a  b  c
A
2p  2p
  2p
  2p


 a  
 b  
 c
2  2
  2
  2

dove
a, b, c
sono i tre lati del triangolo
TRIANGOLO EQUILATERO
FORMULE
H
Caratteristiche
Aˆ  Bˆ  Cˆ  180
Aˆ  Bˆ = Ĉ = 60° ; AC  BC  AB ( lato l)
CH  AB  CHA, CHB triangoli rettangoli uguali
l
AH  HB =   L’altezza è anche mediana della base
2
ACˆ H  BCˆ H = 30°, l’altezza è anche bisettrice
dell’angolo al vertice
2 p  3  l formula diretta per calcolare il perimetro conoscendo il lato
2p
formula inversa per calcolare il lato conoscendo il perimetro
l
3
bh
formula diretta per calcolare l’area conoscendo la base e l’altezza
A
2
2A
formula inversa per calcolare la base conoscendo l’Area e l’altezza
b
h
2A
formula inversa per calcolare l’altezza conoscendo l’Area e la base
h
b
FORMULA DI ERONE (per calcolare Area conoscendo solo i lati)
A
2p  2p
  2p
  2p


 a  
 b  
 c
2  2
  2
  2

l
 3
2
TRIANGOLO SCALENO
I tre lati diversi, possono essere considerati,
indifferentemente,come basi. Quindi avremo altrettante
altezze  ci saranno tre basi e tre altezze:
AH  BC  AH altezza relativa alla base BC
CK  AB  CK altezza relativa alla base AB
BT  AC  BT altezza relativa alla base AC
sono i tre lati del triangolo e 2p è il perimetro
l
2h
( ricorda che
3
3  1,732... )
FORMULE
2 p  l1  l 2  l3 formula diretta per calcolare il perimetro conoscendo i tre lati
bh
formula diretta per calcolare l’area conoscendo la base e l’altezza
A
2
2A
formula inversa per calcolare la base conoscendo l’Area e l’altezza
b
h
2A
formula inversa per calcolare l’altezza conoscendo l’Area e la base
h
b
Caratteristiche

a, b, c
PER IL TEOREMA DI PITAGORA
h
Aˆ  Bˆ  Cˆ  180 , Aˆ  Bˆ  Cˆ
AC  BC  AB quindi AC  l1 , BC  l2 , AB  l3
dove

FORMULA DI ERONE (per calcolare Area conoscendo solo i lati)
2 p è il perimetro
A
2p  2p
  2p
  2p


 a  
 b  
 c
2  2
  2
  2

dove
a, b, c
sono i tre lati del triangolo