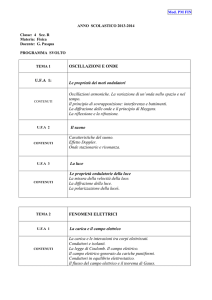
3 Il teorema di Gauss for dummies 3.1 Il flusso di un vettore attraverso una superficie Per una porzione di superficie che sia piana, disposta nello spazio, c’è una direzione che risulta individuata in modo univoco ed è quella della perpendicolare alla superficie stessa. Se lungo tale direzione scegliamo come positiva una delle due possibili orientazioni uscenti, è possibile associare ad ogni superficie piana un vettore di modulo 1. Tale vettore n̂3
n̂
n̂
n̂ 2
n̂1
n̂3
n̂1
n̂ 2
n̂ 4
n̂ 4
figura 3.1 unitario, i cui rappresentanti saranno quindi perpendicolari alla superficie ed uscenti da essa nel verso scelto come positivo, viene detto versore normale e si indica con il simbolo n̂ : in figura 3.1 ne vediamo qualche esempio. La prima delle superfici illustrate è una porzione di piano: l’orientazione che si è scelta come positiva per la normale è quella che viene verso di noi. Le altre due sono esempi di superfici che vengono dette chiuse. Esse hanno la proprietà di separare lo spazio in due regioni, una interna ed una esterna, in modo tale che per passare da una all’altra sia necessario perforare la superficie e scavalcarla. Inoltre, a differenza delle superfici aperte, non sono delimitate da alcuna linea di contorno. Nei semplici casi considerati, le facce di tali superfici chiuse sono tutte porzioni di piano, e convenzionalmente si assume come direzione positiva per la normale quella che va dalla regione interna verso l’esterno. Se la superficie si trova disposta in una regione dello spazio che sia sede di qualche campo vettoriale, come ad esempio un campo elettrico, è possibile sfruttare il versore normale per avere una misura di quanto le linee di campo attraversano la superficie. Si tratta di una informazione non banale, legata sia all’intensità del campo in prossimità della superficie, sia alla direzione della normale rispetto al campo. Come si vede in figura 3.2 dove si è preso in esame il caso semplice di un campo vettoriale costante sia in direzione che in 1
G
v
G
v
n̂
α
n̂
α = 0°
n̂
α = 90°
figura 3.2 intensità, una stessa superficie, se disposta perpendicolarmente alle linee di campo sarà attraversata in maniera proporzionale alla sua estensione, mentre, se disposta di taglio, parallelamente alle linee di campo, non sarà attraversata da nessuna di esse. Nei casi di inclinazione intermedia, il numero di linee di campo che tagliano la superficie sarà tanto maggiore quanto più l’angolo α fra il campo vettoriale in quel punto ed il versore normale alla superficie si avvicinerà a zero, e tanto minore quanto più l’angolo si avvicinerà a 90°. Possiamo quindi costruire una grandezza fisica che ci dia la misura di quanto le linee di G
un campo vettoriale v intercettino una superficie piana disposta nello spazio, semplicemente moltiplicando l’area S della superficie per il coseno dell’angolo α fra il versore normale n̂ ed il campo. Infatti il cos α ha la proprietà che ci occorre, cioè di valere zero quando n̂ è G
G
perpendicolare a v , e di crescere fino ad un valore massimo quando n̂ è parallelo a v . Da G
ultimo moltiplichiamo ancora per l’intensità | v | del campo vettoriale dato che essa è G
tanto maggiore quanto più quanto sono fitte le linee del campo v nello spazio. Abbiamo così costruito la quantità: G
| v | S cos α G
alla quale si dà il nome di flusso del campo v attraverso la superficie piana S. Conoscere il flusso di un campo vettoriale attraverso una superficie piana significa avere un’ informazione che racchiude in sé sia l’intensità del campo nella regione dove si trova S sia l’inclinazione di S rispetto alle linee di campo. Nel caso più generale avremo a che fare con superfici non piane e con campi vettoriali aventi direzione ed intensità non costanti: esprimere il flusso corrispondente risulta complesso. Una via possibile per effettuare il calcolo per superficie curva, come quella in figura, è quella di immaginarla di divisa in tanti quadretti così piccoli, rispetto alla scala di grandezza cui siamo interessati, da far si che essi possano sembrarci delle porzioni di piano. A ciascuno di essi potremo assegnare un versore normale, e poi portare a termine il 2
calcolo del flusso complessivo sommando i flussi elementari attraverso ciascun quadretto. Se con l’indice i contrassegniamo i valori relativi a ciascuna delle porzioni elementari di G
superficie ∆S i , il flusso del campo v attraverso la superficie S sarà: G
∑ ∆Si |v |i cos αi i
n̂
n̂
α
n̂
G
v
In questa espressione tutti i termini della sommatoria dipendono dall’indice i. Infatti, sia G
il valore vi che il campo vettoriale assume in corrispondenza della porzione ∆S i , sia l’angolo αi che esso forma con il versore normale, variano spostandosi lungo la G
superficie. Il flusso del campo vettoriale v attraverso la superficie S si indica in maniera G
compatta attraverso la lettera greca phi: φS (v ) . Per quanto riguarda le superfici chiuse, in base alla convenzione fissata all’inizio del G
paragrafo per la direzione positiva del versore normale, avremo che il flusso di v sarà positivo per le linee di campo che escono dal volume racchiuso, e negativo per quelle che vi entrano. Sfrutteremo ora questo nuovo strumento matematico per esprimere in modo diverso le proprietà del campo elettrico. Mostreremo che la legge di Coulomb, che esprime la G
dipendenza del campo E generato da una carica puntiforme dall’inverso del quadrato G
della distanza dalla posizione della carica, risulta legata ad una proprietà del flusso di E attraverso una superficie chiusa nel modo seguente: TEOREMA DI GAUSS G
G
IL FLUSSO φS (E ) DEL CAMPO ELETTRICO E DI UNA DISTRIBUZIONE DI CARICHE Q1, Q2, …, QN ATTRAVERSO UNA QUALUNQUE SUPERFICIE CHIUSA S, È DATO DALLA SOMMA DELLE CARICHE INTERNE AD S, DIVISA PER ε0 , CIOÈ: G
Qiinterne
∑
φS (E ) =
ε0
Dimostreremo il teorema solo nel caso semplificato in cui si abbia una carica puntiforme Q e si voglia calcolare il flusso del campo elettrico attraverso una sfera centrata in Q. Avendo suddiviso la superficie in tratti elementari piani, ed individuato per ciascuno di essi un vettore superficie così definito: 3
JJJG
∆S i = ∆Si nˆi
G
avremo che in ogni porzione il campo elettrico di Q JJJG
E
sarà parallelo al versore normale e quindi a ∆S i . In tale modo cos αi = 1 per ciascuno dei termini della sommatoria che figurano nell’espressione del flusso, da cui: G
JG
φsfera (E ) = ∑ ∆Si Ei cos αi = ∑ ∆Si
i
i
JJJG
∆S G
E
JJJG
∆S
Q
1 Q
4πε0 r 2
G
avendo sostituito al modulo del campo elettrico la sua espressione Ei =
1 Q
che non 4πε0 r 2
dipende dalla particolare porzione di superficie sferica ∆Si ma solo dal raggio della sfera. Raccogliendo a fattor comune i termini che non dipendono dall’indice della sommatoria, e ricordando che la superficie di una sfera di raggio r vale ∑ ∆Si = 4πr 2 , otteniamo: i
JG
φsfera (E ) =
1 Q
4πε0 r 2
∑ ∆S
i
i
=
1 Q
Q
4πr 2 = 2
4π ε0 r
ε0
che è proprio quanto afferma il teorema di Gauss, dato che l’unica carica interna alla sfera è la carica Q. Va sottolineato che il teorema di Gauss viene dimostrato, anche nel caso più generale, G
sfruttando solamente il fatto che il campo E dipende dall’inverso del quadrato della distanza dalla sua sorgente puntiforme. Pertanto esso rappresenta una proprietà valida 1
per tutti i campi radiali con intensità proporzionale a 2 , anche quelli che non hanno r
1
simmetria sferica . 1
G
In particolare il teorema di Gauss si applica al campo gravitazionale g = −
G
GM
rˆ , formalmente identico r2
1
viene occupato da −G e quello delle cariche dalla massa. Da un 4πε0 G
interne
semplice raffronto si ha allora φS (g ) = −4πG ∑ M i
.
ad E , dove però il ruolo di 4
ESEMPIO 1 Data la distribuzione di cariche a lato vogliamo calcolare il flusso del campo elettrico attraverso le quattro superfici S1, S2, S3, S4. Si assuma: q1 = q 3 = 0.30 µC , q1
q3
−6
q 3 = −2.0 × 10 C , q 4 = −1.00 µC . S1
S4
S2
q4
Applicando il teorema di Gauss per il quale è G
∑Qiinterne , q2
φSchiusa (E ) =
sapendo che ε0
ε0 = 8.85 × 10−12
Nm2
si ottiene: C2
S3
2
G
q
−2.0 × 10−6 C
6 Nm
φS 1(E ) = 3 =
≈
−
0.23
×
10
ε0
8.85 × 10−12 C2/Nm2
C
2
G
q + q4
0.30 × 10−6 C − 1.00 × 10−6 C
6 Nm
φS 2 (E ) = 2
=
≈
−
0.08
×
10
ε0
8.85 × 10−12 C2/Nm2
C
G
0.00
Nm2
φS 4 (E ) =
= 0.00
ε0
C
2
G
q
0.30 × 10−6 C
6 Nm
. φS 3 (E ) = 2 =
≈
0.03
×
10
ε0
8.85 × 10−12 C2/Nm2
C
ESEMPIO 2 n̂
G
Calcoliamo il flusso di un campo elettrico costante E
60°
in direzione ed intensità come quello in figura, di G
N
modulo E = 2.0 × 103 ,attraverso una superficie C
piana, a sezione quadrata di lato l = 5.0 m , il cui versore normale forma un angolo di 60° con le linee di forza del campo. G
JG
⎛
N⎞ 1
Nm2
φ(E ) = ∆S E cos 60° = 25m2 ⎜⎜2.0 × 103 ⎟⎟⎟ = 25 × 103
⎝
C⎠ 2
C
(
)
5