Facoltà di Ingegneria
Prova Scritta di Fisica I
29 Giugno 2004 - Compito A
Quesito n. 1
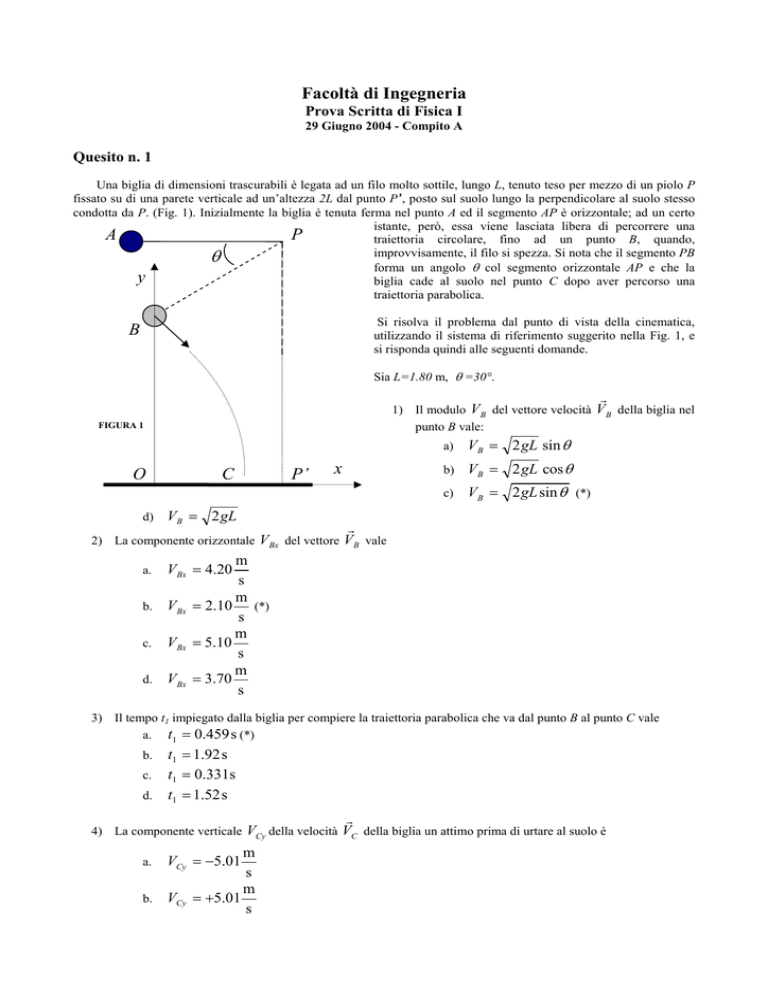
Una biglia di dimensioni trascurabili è legata ad un filo molto sottile, lungo L, tenuto teso per mezzo di un piolo P
fissato su di una parete verticale ad un’altezza 2L dal punto P’, posto sul suolo lungo la perpendicolare al suolo stesso
condotta da P. (Fig. 1). Inizialmente la biglia è tenuta ferma nel punto A ed il segmento AP è orizzontale; ad un certo
istante, però, essa viene lasciata libera di percorrere una
A
P
traiettoria circolare, fino ad un punto B, quando,
improvvisamente,
il filo si spezza. Si nota che il segmento PB
θ
forma un angolo θ col segmento orizzontale AP e che la
y
biglia cade al suolo nel punto C dopo aver percorso una
traiettoria parabolica.
Si risolva il problema dal punto di vista della cinematica,
utilizzando il sistema di riferimento suggerito nella Fig. 1, e
si risponda quindi alle seguenti domande.
B
Sia L=1.80 m, θ =30°.
1) Il modulo V B del vettore velocità
punto B vale:
FIGURA 1
O
d)
C
P’
VB = 2 gL
2) La componente orizzontale
x
a)
VB = 2gL sin θ
b)
VB = 2gL cos θ
c)
VB = 2gL sin θ (*)
r
V B della biglia nel
r
VBx del vettore V B vale
m
s
m
= 2.10 (*)
s
m
= 5.10
s
m
= 3.70
s
a.
VBx = 4.20
b.
VBx
c.
VBx
d.
VBx
3) Il tempo t1 impiegato dalla biglia per compiere la traiettoria parabolica che va dal punto B al punto C vale
a. t1 = 0.459 s (*)
t1 = 1.92 s
c. t1 = 0.331s
d. t1 = 1.52 s
b.
4) La componente verticale
r
VCy della velocità VC della biglia un attimo prima di urtare al suolo è
m
s
m
= +5.01
s
a.
VCy = −5.01
b.
VCy
m
(*)
s
m
= +8.13
s
c.
VCy = −8.13
d.
VCy
5) La distanza d del punto C (di impatto della biglia al suolo) e il punto P’ vale
d
d
d
d
a.
b.
c.
d.
= 1.37 m
= 2.15 m
= 0.595 m (*)
= 0.370 m
Quesito n. 2
B
FIGURA2
µ
Piano liscio
V0
h
Piano scabro
θ
A
θ
C
Un blocco di massa m di piccole dimensioni viene lanciato, all’istante di tempo t=0 s e con velocità
V0 , dal punto
A, posto alla base di un piano inclinato di un angolo θ rispetto all’orizzontale (Fig. 2), lungo il piano stesso. Esso
raggiunge la sommità del piano alla quota h nel punto B, dove si ferma, restando in bilico. Successivamente, il blocco
inizia a scendere lungo un secondo piano, questa volta scabro, inclinato anch’esso di θ rispetto all’orizzontale. Il
coefficiente di attrito dinamico tra il blocco e il secondo piano è pari a µ. Dopo aver ben individuato la dinamica del
blocco da A a C, si risponda alle seguenti domande.
Sia m =1.00 Kg, θ =30°, h =2.00 m, µ =0.200.
6) Il valore della velocità V0 da imprimere al blocco perché esso arrivi in B a velocità nulla è
a.
V0 = 2 g h
b.
V0 =
c.
V0 =
d.
V0 = 2 gh (*)
2g
h
2h
g
t * impiegato dal blocco in A per raggiungere il punto B è
1
2h
*
a. t =
cos θ g
7) Il tempo
b.
t* =
1
sin θ
2h
(*)
g
1
2g
cos θ h
1
*
d. t =
2 gh
sin θ
c.
t* =
8) La forza di attrito che il secondo piano esercita sul blocco ha modulo pari a
a.
f t = 7.10 N
f t = 5.60 N
f t = 1.70 N (*)
f t = 0.908 N
b.
c.
d.
9) Il modulo della velocità del blocco nel punto C vale
a.
b.
c.
d.
m
(*)
s
m
VC = 55.1
s
m
VC = 8.34
s
m
VC = 6.10
s
VC = 5.06
10) L’energia dissipata dal blocco lungo l’intera discesa è, in valore assoluto, pari a
a. E d = 6.79 J (*)
E d = 8.98 J
E d = 5.34 J
E d = 4.75 J
b.
c.
d.
Quesito n. 3
FA
B
R
θ
R
M
FIGURA 3
r
FA costante, applicata, ad un angolo θ rispetto
r
all’orizzontale, alla maniglia B, così come mostrato nella Fig. 3. Partendo da fermo e sottoposto alla forza FA , il
Un grosso rullo viene azionato manualmente attraverso una forza
cilindro del rullo, di massa M e raggio R, rotola senza strisciare su di un piano scabro orizzontale, fino a raggiungere, in
un intervallo di tempo ∆t, la velocità angolare ωf. Successivamente, per fermare il rullo, si applica, allo stesso modo di
prima, un forza
r
r
FB = −2 FA . Tale forza agisce fintanto che il centro di massa del cilindro non viene posto a riposo.
Si risolva il problema dinamico, assumendo che i perni, ai quali sono collegati le aste che trasmettono la forza
applicata, siano privi di attrito e che le aste stesse e la maniglia siano di massa trascurabile. Si assuma ancora che il
cilindro sia pieno. Si risponda infine alle seguenti domande.
Sia M=500 Kg, R =0.500 m, FA=400 N, θ =30°, ωf =15.0 rad/s.
11) L’accelerazione angolare α del cilindro, espressa in termini del modulo FA della forza applicata, è
a.
b.
α=
α=
2 FA
5MR
FA
(*)
3MR
F
c. α = A MR
2
FA
d. α =
3MR
12) L’intervallo di tempo ∆t necessario per portare il cilindro a ruotare alla velocità angolare ωf vale
a. ∆t = 25.1 s
b. ∆t = 5.72 s
c. ∆t = 31.6 s
d. ∆t = 16.2 s (*)
13) La forza di attrito esercitata sul cilindro vale
a.
f t = 2 FA
b.
c.
d.
ft =
ft =
2 FA
3
FA
(*)
2 3
F
ft = A
3
14) La reazione vincolare normale al piano vale:
a.
N = 5200 N
b. N = 6500 N
c. N = 4700 N (*)
d. N = 3300 N
15) L’intervallo di tempo ∆t ′ necessario a fermare il rullo, dopo che esso ha raggiunto la velocità angolare ωf, vale
a. ∆t ′ = 8.12 s (*)
b. ∆t ′ = 5.53 s
c. ∆t ′ = 18.1 s
d. ∆t ′ = 0.172 s
Altre domande:
16) Lungo la curva sopraelevata disegnata in figura, supposta circolare e di raggio R=200m, in una strada larga 12
m (lato BC del triangolo BAC in figura) e realizzata in modo tale da avere coefficiente di attrito trascurabile, il
limite di velocità è di vmax=100 km/h. Calcolare di quanto il bordo esterno della strada, lato BA, debba essere
rialzato rispetto a quell’interno, affinché l’autovettura, procedendo alla massima velocità consentita, non sbandi
uscendo fuori strada.
a. h = 4.3m (*)
b. h = 5.7 m
c. h = 2.4 m
d. h = 1.8 m
F
FIGURA 4
R
B
F
R
O
b
A
θ
C
17) Il teorema di Koenig dell’energia cinetica per un sistema di punti materiali afferma che
a. L’energia cinetica totale è sempre nulla
b. L’energia cinetica totale è uguale all’energia cinetica del CM del sistema.
c. L’energia cinetica totale misurata rispetto ad un sistema di riferimento inerziale è uguale alla somma
dell’energia cinetica del CM del sistema e dell’energia cinetica totale misurata rispetto ad un sistema
di riferimento solidale con il CM (*)
d. L’energia cinetica totale è uguale all’energia cinetica totale del sistema rispetto ad un sistema di
riferimento solidale con il CM.
18) Per un punto materiale in moto con velocità angolare costante ω lungo una traiettoria circolare piana si
conservano le seguenti grandezze fisiche:
a. Il momento angolare rispetto al centro della traiettoria e l’energia cinetica (*)
b. La quantità di moto e l’energia cinetica
c. Il momento angolare rispetto al centro della traiettoria e la quantità di moto
d. Nessuna
19) All’istante iniziale una ruota, assimilabile ad un anello, un disco omogeneo ed una sfera, omogenea , tutti e tre
di massa M e raggio R, sono posizionati fermi in cima ad un piano inclinato di lunghezza L e angolo θ. Se essi
vengono lasciati liberi e si muovono lungo il piano inclinato con moto di puro rotolamento, determinare la
velocità con cui il CM di ciascuno arriva in fondo al piano inclinato.
4
10
gh ; vCM , Sfera =
gh (*)
3
7
2
7
=
gh ; vCM , Sfera =
gh
3
5
a.
vCM , Anello = gh ; vCM , Disco =
b.
vCM , Anello =
3
gh ; vCM , Disco
2
5
1
gh ; vCM , Sfera =
gh
3
7
1
1
=
gh ; vCM , Sfera =
gh
3
7
c.
vCM , Anello = 2 gh ; vCM , Disco =
d.
vCM , Anello = gh ; vCM , Disco
20) Un moto rettilineo (posizione x, velocità v, accelerazione a) è armonico quando l’accelerazione è
a. a = costante
b. a = − kx con k=costante (*)
c.
d.
a = −kx 2 con k=costante
a = − kv con k=costante
Soluzione
Quesito n. 1
Una biglia di dimensioni trascurabili è legata ad un filo molto sottile, lungo L, tenuto teso per mezzo di un piolo P
fissato su di una parete verticale ad un’altezza 2L dal punto P’, posto sul suolo lungo la perpendicolare al suolo stesso
condotta da P. (Fig. 1). Inizialmente la biglia è tenuta ferma nel punto A ed il segmento AP è orizzontale; ad un certo
istante, però, essa viene lasciata libera di percorrere
A
P
y
una traiettoria circolare, fino ad un punto B, quando,
improvvisamente, il filo si spezza. Si nota che il
θ
segmento PB forma un angolo θ col segmento
orizzontale AP e che la biglia cade al suolo nel punto
C dopo aver percorso una traiettoria parabolica.
FIGURA 1
Sia L=1.80 m, θ =30°.
2L
B
θ
16) Per la conservazione dell’energia si ha:
E A = E B ⇒ mgL sin θ =
L(2-sinθ)
1
mV B2 .
2
VB del vettore velocità
r
V B della biglia nel punto B vale:
In questo modo, il modulo
O
C
P’
VB = 2gL sin θ
x
17) La componente orizzontale
VBx del vettore
r
m
V B vale V Bx = 2 gL sin θ sin θ = 2.10 .
s
18) Il tempo t1 impiegato dalla biglia per compiere la traiettoria parabolica che va dal punto B al punto C può essere
calcolato facendo riferimento al sistema di coordinate cartesiane indicato in Fig. 1. Scriviamo allora la legge
oraria del moto per la biglia dopo che il filo si spezza ( t ≥ 0 s ):
x(t ) = VBx t
1 2,
y (t ) = y 0 + VBy t − 2 gt
ove V By = − 2 gL sin θ cos θ = −
3gL
2
(1)
e y 0 = L(2 − sin θ ) .
Imponendo adesso y(t)=0 e risolvendo l’equazione di secondo grado che ne deriva, si ha
5 − 1 3L
= 0.459 s .
2
g
t1 =
19) Per trovare la componente verticale VCy della velocità
r
VC della biglia un attimo prima di urtare al suolo,
deriviamo la legge oraria del moto rispetto al tempo, ottenendo:
V x (t ) = VBx
.
V y (t ) = VBy − gt
(2)
Se adesso poniamo t=t1 nella seconda espressione della (2), si ha:
VCy = V y (t1 ) = −8.13
m
.
s
20) Per trovare la distanza d tra il punto C (di impatto della biglia al suolo) e il punto P’ , ci si calcola dapprima la
distanza OC, sostituendo t1 nella prima espressione della (1). Sottraendo la distanza così trovata ad OP’=Lcosθ
si ha:
d = 0.595 m .
Quesito n. 2
B
FIGURA2
µ
Piano liscio
V0
h
Piano scabro
θ
A
θ
C
Un blocco di massa m di piccole dimensioni viene lanciato, all’istante di tempo t=0 s e con velocità
V0 , dal punto
A, posto alla base di un piano inclinato di un angolo θ rispetto all’orizzontale (Fig. 2), lungo il piano stesso. Esso
raggiunge la sommità del piano alla quota h nel punto B, dove si ferma, restando in bilico. Successivamente, il blocco
inizia a scendere lungo un secondo piano, questa volta scabro, inclinato anch’esso di θ rispetto all’orizzontale. Il
coefficiente di attrito dinamico tra il blocco e il secondo piano è pari a µ.
Sia m =1.00 Kg, θ =30°, h =2.00 m, µ =0.200.
21) Il valore della velocità V0 da imprimere al blocco perché esso arrivi in B a velocità nulla si trova imponendo
conservazione dell’energia meccanica
E A = EB ⇒
1
mV02 = mgh ⇒ V0 = 2 gh .
2
*
22) Il tempo t impiegato dal blocco in A per raggiungere il punto B si trova notando innanzitutto che la sua
accelerazione lungo il piano è a = − g sin θ . La velocità del blocco sarà quindi:
V (t ) = V0 − ( g sin θ ) t .
Imponendo adesso V(t)=0, si ottiene
t* =
1
sin θ
2h
.
g
23) La forza di attrito che il secondo piano esercita sul blocco ha modulo pari a
f t = µN = µ mg cos θ = 1.70 N
24) Il modulo della velocità del blocco nel punto C può essere trovato attraverso il teorema dell’energia cinetica
come segue. Scriviamo quindi
1
h
h
2
EC − E B = − f t
.
⇒ mVC − mgh = − µmg cos θ
2
sin θ
sin θ
Semplificando opportunamente l’espressione di sopra e risolvendo per Vc, si ha
VC = 5.06
m
s
25) L’energia dissipata dal blocco lungo l’intera discesa è, in valore assoluto, pari a
h
Ed = f t
= 6.79 J .
sin θ
Quesito n. 3
FA
B
R
θ
R
M
FIGURA 3
r
Un grosso rullo viene azionato manualmente attraverso una forza FA costante, applicata, ad un angolo θ rispetto
r
all’orizzontale, alla maniglia B così come mostrato nella Fig. 3. Partendo da fermo e sottoposto alla forza FA , il
cilindro del rullo, di massa M e raggio R, rotola senza strisciare su di un piano scabro orizzontale, fino a raggiungere, in
un intervallo di tempo ∆t, la velocità angolare ωf. Successivamente, per fermare il rullo, si applica, allo stesso modo di
r
r
prima, un forza FB = −2 FA . Tale forza agisce fintanto che il centro di massa del cilindro non viene posto a riposo. Si
risolva il problema dinamico, assumendo che i perni, ai quali sono collegati le aste che trasmettono la forza applicata,
siano privi di attrito e che le aste stesse e la maniglia siano di massa trascurabile. Si assuma ancora che il cilindro sia
pieno.
Sia M=500 Kg, R =0.500 m, FA=400 N, θ =30°, ωf =15.0 rad/s.
26) Per trovare l’accelerazione angolare α del cilindro, espressa in termini del modulo FA della forza applicata, si
può scrivere:
I P 'α = M P ' ⇒
Risolvendo adesso per α si ha
3
MR 2α = FA cos θ R .
2
α=
FA
.
3MR
27) L’intervallo di tempo ∆t necessario per portare il cilindro a ruotare alla velocità angolare ωf si può trovare
ricorrendo all’espressione cinematica per la velocità angolare ω seguente:
ω (t ) = αt + ω 0 , ove ω 0 = 0 ⇒ ω f = α∆t =
FA
3MR
∆t ⇒ ∆t =
3MR
ω f = 16.2 s .
FA
28) La forza di attrito esercitata sul cilindro può essere trovata attraverso l’applicazione del teorema del centro di
massa al cilindro. Pertanto, osservando il diagramma delle forze in Fig. 4, possiamo scrivere:
Fxext = Ma CM ⇒ FA cos θ − f t = MRα
Risolvendo adesso per ft, conoscendo FA ed α, possiamo scrivere
FIGURA 4
y
FA
θ
N
ft =
.
2 3
29) La reazione vincolare normale al piano può essere trovata
eguagliando a zero la componente y della risultante delle forze,
cosicché:
Fyext = 0 ⇒ N + FA sin θ − Mg = 0 .
x
Mg
FA
ft
Risolvendo per N e sostituendo i valori, si ha:
N = 4700 N .
30) L’intervallo di tempo ∆t ′ necessario a fermare il rullo, dopo che esso ha raggiunto la velocità angolare ωf, si
può trovare notando che l’accelerazione angolare adesso deve essere negativa e pari a α ′ = −2α . Dalla
cinematica rotazionale, allora, si ha
Ponendo adesso
ω (∆t ′) = 0 , si ha
ω (t ) = α ′t + ω f .
∆t ′ = −
ω f ∆t
=
= 8.12 s .
α′
2