Strumenti informatici 5.3 - Realizzare un test per proporzioni dipendenti
in Excel ed SPSS
Excel non dispone di una funzione che consenta di realizzare il test statistico presentato nella
sezione 2.1.2. SPSS, invece, permette di realizzare il test di McNemar (McNemar, 1947), che
nient’altro è che la trasformazione a X2 del punto z calcolato nella sezione 2.1. Ossia, se la
n −n
trasformazione z avveniva con la formula z = 21 12 , il test di McNemar consiste
n 21 + n12
nell’elevamento al quadrato di questa espressione. Poiché la distribuzione χ2 nient’altro è che una
(n21 − n12 )2
somma di punti z al quadrato (vedi Capitolo 4), il valore
, è distribuito come χ2 con 1
n 21 + n12
grado di libertà. Ad ogni modo, il modulo di SPSS che esegue l’analisi si basa sulla distribuzione
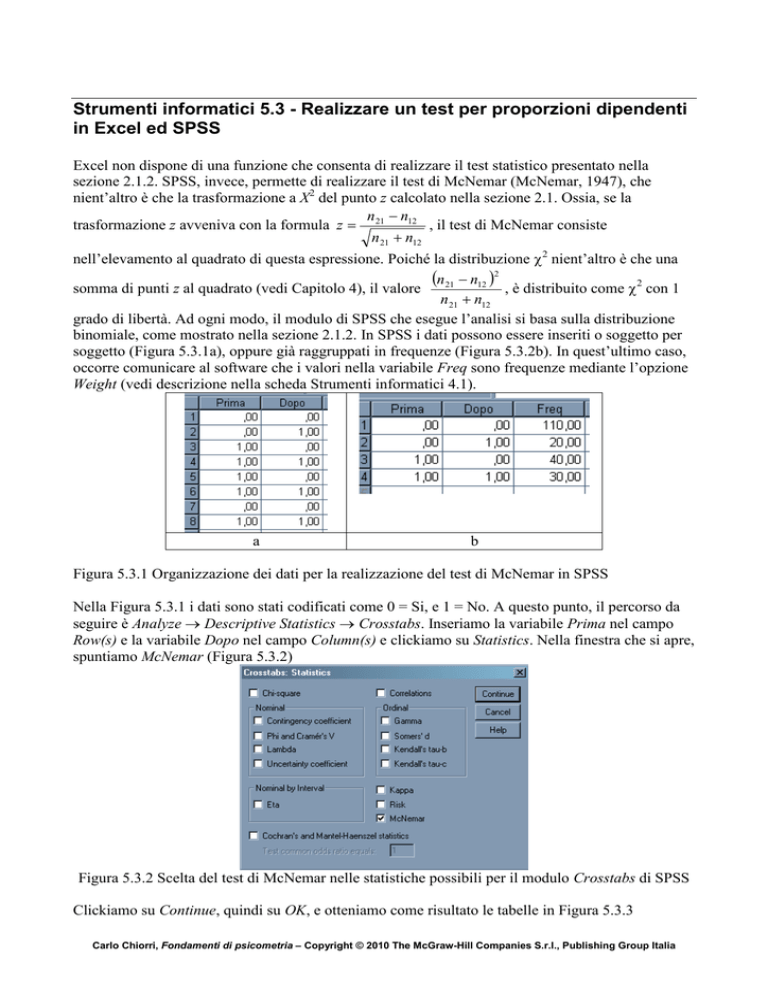
binomiale, come mostrato nella sezione 2.1.2. In SPSS i dati possono essere inseriti o soggetto per
soggetto (Figura 5.3.1a), oppure già raggruppati in frequenze (Figura 5.3.2b). In quest’ultimo caso,
occorre comunicare al software che i valori nella variabile Freq sono frequenze mediante l’opzione
Weight (vedi descrizione nella scheda Strumenti informatici 4.1).
a
b
Figura 5.3.1 Organizzazione dei dati per la realizzazione del test di McNemar in SPSS
Nella Figura 5.3.1 i dati sono stati codificati come 0 = Si, e 1 = No. A questo punto, il percorso da
seguire è Analyze → Descriptive Statistics → Crosstabs. Inseriamo la variabile Prima nel campo
Row(s) e la variabile Dopo nel campo Column(s) e clickiamo su Statistics. Nella finestra che si apre,
spuntiamo McNemar (Figura 5.3.2)
Figura 5.3.2 Scelta del test di McNemar nelle statistiche possibili per il modulo Crosstabs di SPSS
Clickiamo su Continue, quindi su OK, e otteniamo come risultato le tabelle in Figura 5.3.3
Carlo Chiorri, Fondamenti di psicometria – Copyright © 2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Prima * Dopo Crosstabulation
Count
Dopo
Si
Prima
Si
No
No
110
40
150
Total
20
30
50
Total
130
70
200
Chi-Square Tests
Value
McNemar Test
N of Valid Cases
Exact Sig.
(2-sided)
,013a
200
a. Binomial distribution used.
Figura 5.3.3 Output di SPSS per il test di McNemar per due proporzioni dipendenti (la tabella Case
Processing Summary è omessa)
Nella prima tabella osserviamo la tabella di contingenza Prima × Dopo, mentre nella seconda (ChiSquare Tests), troviamo la probabilità a due code per i dati in esame (per ottenere quella ad una
coda basta dividere Exact Sig. (2-sided) per due).
Quando la variabile dipendente non è dicotomica, occorre utilizzare il modello della
Marginal Homogeneity, che è disponibile in SPSS. Supponiamo che le opzioni di risposta degli
studenti alla proposta di iscriversi al Nuovo Ordinamento fossero tre (0 = No, 1 = Indeciso; 2 = Sì),
come in Tabella 5.3.1
Tabella 5.3.1 Intenzione di passare al Nuovo Ordinamento di 200 studenti del secondo anno di un
corso di laurea in Scienze e Tecniche Psicologiche
Dopo la conferenza
Prima della
conferenza
No
No
Indeciso
Si
Totale
15
10
25
50
Indeciso
10
20
30
60
Si
10
15
65
90
Totale
35
45
120
200
In questo caso i dati possono essere organizzati come in Figura 5.3.1a o 5.3.2b. Il percorso da
seguire per realizzare l’analisi però è un altro, ossia Analyze → Nonparametric Tests → 2 Related
Samples (Figura 5.3.4).
Carlo Chiorri, Fondamenti di psicometria – Copyright © 2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Figura 5.3.4 Percorso di SPSS per realizzare un test di Marginal Homogeneity
Nella finestra che si apre occorre selezionare le variabili da confrontare clickandoci sopra col tasto
sinistro del mouse, e poi spostarle nel campo Test Pair(s) List col tasto
(Figura 5.3.5).
Figura 5.3.5 Impostazione dell’analisi Mariginal Homogeneity in SPSS
I tasti Exact e Options offrono le stesse opzioni del test della binomiale, mentre gli altri test sono il
Wilcoxon (che è presentato nella sezione 2.2), il test dei segni (Sign) e il McNemar che abbiamo già
visto.
L’output è riportato in Figura 5.3.6
Marginal Homogeneity Test
Distinct Values
Off-Diagonal Cases
Observed MH Statistic
Mean MH Statistic
Std. Deviation of MH
Statistic
Std. MH Statistic
Asymp. Sig. (2-tailed)
Prima & Dopo
3
100
90,000
112,500
7,159
-3,143
,002
Carlo Chiorri, Fondamenti di psicometria – Copyright © 2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Figura 5.3.6 Output dell’analisi Mariginal Homogeneity in SPSS
La tabella in Figura 5.3.6 indica che vi è stata una variazione significativa nelle risposte degli
studenti prima e dopo la conferenza (Asymp. Sig. (2-tailed) < ,05).
Si noti ad ogni modo che questo test statistico, così eseguito, può non consentire un’analisi
particolarmente approfondita dei dati, in quanto è basato, come dice il nome, sulle proporzioni
marginali della tavola di contingenza che riassume i dati (vedi Tabella 5.3.1). Nondimeno, certi tipi
di cambiamento (ad esempio da No a Sì) potrebbero essere meno probabili di altri (ad esempio, da
No a Indeciso), e questo tipo di analisi non permette di tenerne conto. Il lettore interessato al
problema può trovare maggiori informazioni, ad esempio, in Corbetta (1992).
In una tesi di laurea o in un articolo scientifico riporteremmo il grafico in Figura 5.14a, al tabella in
Figura 5.3.3 e scriveremmo:
Per verificare se la proporzione di 200 studenti intenzionati ad iscriversi al nuovo ordinamento,
inizialmente di ,65, era stata modificata dall’aver assistito dalla conferenza di presentazione dei
vantaggi del cambiamento (P post-conferenza = ,75) è stato eseguito un test di McNemar, che ha
rivelato che dopo la conferenza la proporzione di studenti intenzionati ad iscriversi al nuovo
ordinamento era statisticamente aumentata (z = 2,58, p < ,05, h = 0,28) [oppure, X2(1, n = 200) =
6,66, p < ,05, h = 0,28)].
Carlo Chiorri, Fondamenti di psicometria – Copyright © 2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia












