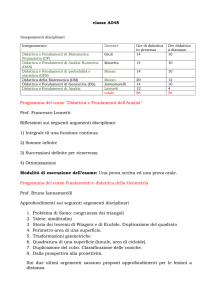
classe A047 MATEMATICA
Insegnamenti disciplinari
Insegnamento
Docente
Scoppola
Manetta
Ore di didattica
in presenza
14
14
Ore didattica
a distanza
10
10
Didattica
Didattica
(DAN)
Didattica
statistica
Didattica
Didattica
Didattica
e Fondamenti di Algebra (DAL)
e Fondamenti di Analisi Numerica
e Fondamenti di probabilità e
(DPS)
della Matematica (DM)
e Fondamenti di Geometria (DG)
e Fondamenti di Analisi
Maran
14
10
Maran
Iannamorelli
Leonetti
totale
20
14
12
88
12
10
4
56
Programma del corso "Didattica e Fondamenti dell'Analisi"
Prof. Francesco Leonetti
Riflessioni sui seguenti argomenti disciplinari
1) Integrale di una funzione continua
2) Somme infinite
3) Successioni definite per ricorrenza
4) Ottimizzazione
Modalità di esecuzione dell’esame: Una prova scritta ed una prova orale.
Programma del corso Fondamenti e didattica della Geometria
Prof. Bruno Iannamorelli
Approfondimenti sui seguenti argomenti disciplinari
1.
2.
3.
4.
5.
6.
7.
8.
Problema di Samo: congruenza dei triangoli
Talete: similitudini
Storia dei teoremi di Pitagora e di Euclide. Duplicazione del quadrato
Perimetro-area di una superficie.
Trasformazioni geometriche
Quadratura di una superficie (lunule, arco di cicloide).
Duplicazione del cubo. Classificazione delle coniche.
Dalla prospettiva alla proiettività.
Sui due ultimi argomenti saranno proposti approfondimenti per le lezioni a
distanza.
Modalità di esecuzione dell’esame: Una prova scritta ed una prova orale.
Programma del corso Didattica della Matematica
Prof. Daniele Maran
Introduzione alla didattica della matematica
Il contratto didattico
Conflitti. Misconcezioni. Modelli intuitivi. Modelli parassiti.
Immagini, modelli e schemi
Concetti. Ostacoli
Triangolo di Chevallard-Joshua: polo allievo, polo sapere e polo insegnante.
Trasposizione didattica
Intuizione e dimostrazione
Modalità di esecuzione dell’esame: Una prova scritta ed una prova orale.
Programma del corso Didattica e Fondamenti di Analisi Numerica
Prof. Manuela Manetta
Il corso si propone di ripercorrere i concetti fondamentali della Matematica
Numerica, fornendo spunti metodologico-didattici e riflessioni sull’apprendimento
dei seguenti concetti disciplinari:
Introduzione alla Matematica Numerica
Condizionamento dei problemi e stabilità dei metodi numerici.
Sorgenti di errore nei modelli computazionali.
Rappresentazione dei numeri sul calcolatore.
Matrici e Sistemi Lineari
Richiami di algebra lineare: vettori, matrici e loro proprietà.
Metodi diretti per la soluzione di sistemi lineari: sistemi triangolari, metodo
di eliminazione di Gauss, pivoting. Fattorizzazione LU e fattorizzazione di
Cholesky.
Condizionamento dei sistemi lineari.
Soluzione di Equazioni Non Lineari e Minimizzazione
Approccio geometrico: bisezione, secanti e tangenti.
Metodi iterativi: generalità, convergenza e criteri d'arresto.
Minimizzazione non vincolata: metodo di Newton e varianti.
Interpolazione ed approssimazione
Interpolazione polinomiale: forma di Lagrange.
Differenze divise di Newton e loro proprietà.
Errori d’interpolazione.
Interpolazione mediante polinomi a tratti, splines.
Integrazione Numerica
Formule di quadratura.
Formule di Newton-Cotes.
Polinomi ortogonali, formule Gaussiane e condizioni di stabilità.
Programma a Distanza - Utilizzo di Matlab per implementare metodi
numerici
Introduzione a Matlab: Interfaccia Matlab, prime istruzioni, errori e help;
definizione di variabili, valutazioni di funzioni in un punto o in un vettore;
m-files: script e function; cicli.
Manipolazione di Matrici: costruire una matrice, selezionarne una parte,
speciali classi di matrici, notazione colon, sottomatrici, divisione tra
matrici, risoluzione di un sistema lineare.
Esercizi e funzioni da implementare sul calcolatore riguardanti l'intero
programma svolto.
Modalità di esecuzione dell’esame: Una prova scritta ed una prova orale.
Programma del corso Didattica e Fondamenti di probabilità e statistica
Prof. Daniele Maran
Riflessioni da un punto di vista critico-metodologico e didattico sui seguenti
argomenti
Elementi di statistica
Moda, media, mediana.
Introduzione alla probabilità: il problema della divisione della posta in gioco
Calcolo combinatorio
Definizione di probabilità
Probabilità condizionata
Teorema di Bayes
Probabilità e paradossi
Modalità di esecuzione dell’esame: Una prova scritta ed una prova orale.
Programma del corso Didattica e Fondamenti di Algebra
Prof. Carlo Maria Scoppola
Lezione 1 (tre ore di teoria, in presenza, e due ore da svolgere individualmente o a
gruppi).
I numeri: naturali, interi, razionali, reali, complessi. I procedimenti di estensione.
L'arricchimento della struttura algebrica nelle progressive estensioni e le tecniche
per eseguirle: l'aritmetica elementare negli interi, la costruzione del campo dei
quozienti, le estensioni algebriche, i completamenti.
Un problema classico: le costruzioni con riga e compasso. Esempi ed esercizi.
Assegnazione degli esercizi da svolgere a casa.
Lezione 2 (quattro ore di teoria ed esercizi, in presenza, e tre ore di esercizi da
svolgere individualmente o a gruppi). Il problema della risoluzione delle equazioni
algebriche sul campo razionale. Equazioni quadratiche, cubiche e quartiche. Il
teorema di Ruffini-Abel. I fondamenti della teoria di Galois: il gruppo di Galois, la
corrispondenza di Galois, il lemma di Artin. Nozioni elementari di teoria dei
gruppi finiti: omomorfismi, quozienti, gruppi risolubili, il teorema di JordanHoelder, i gruppi semplici. Il programma di Hoelder e la classificazione dei gruppi
semplici finiti. Esempi ed esercizi. Revisione e correzione degli esercizi assegnati
nella lezione precedente. Assegnazione degli esercizi da svolgere a casa.
Lezione 3 (tre ore di teoria ed esercizi, in presenza, e cinque ore di esercizi da
svolgere individualmente o a gruppi). Il teorema fondamentale della
corrispondenza di Galois, stabilita' e normalita', I campi di spezzamento,
separabilita' e campi di spezzamento, chiusura normale. Esempi ed esercizi.
Revisione e correzione degli esercizi assegnati nella lezione precedente.
Assegnazione degli esercizi da svolgere a casa.
Lezione 4 (quattro ore di teoria ed esercizi, in presenza). La risolubilita' per
radicali delle equazioni algebriche. La semplicita' del gruppo alterno, la
irrisolubilita' del gruppo simmetrico. Equazioni di quinto grado che non sono
risolubili per radicali. Campi finiti. Estensioni ciclotomiche. Esempi ed esercizi.
Revisione e correzione degli esercizi assegnati nella lezione precedente.
Modalità di esecuzione dell’esame: Una prova scritta ed una prova orale.