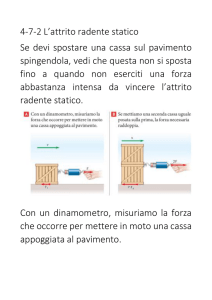
Forza di attrito radente statico
La forza di attrito radente statico si manifesta alla superficie di contatto tra due corpi. Per comprendere la natura
di tale forza, si faccia riferimento alla semplice situazione in cui un corpo di massa m è poggiato su un piano
orizzontale. Fenomenologicamente, la presenza dell’attrito è dimostrata dal fatto che, pur applicando una forza
r
esterna Fext parallela al piano, il corpo non si muove.
Il valore assunto dalla forza d’attrito dipende esclusivamente dal valore di Fext , come si vede risolvendo
l’equazione che esprime la II legge di Newton per la statica:
F ext + Fa + R + P = 0
Proiettando sugli assi, si ottengono le equazioni:
Fext − Fa = 0
R −P=0
Dalla prima si ottiene:
Fa = Fext
Il fatto che Fa dipenda esclusivamente dalla forza applicata Fext è del tutto logico, se si pensa che, per mantenere
la condizione di statica, più Fext spinge forte, più grande deve essere l’azione resistente dell’attrito.
Al di là di questo esempio, resta vero in generale che la forza di attrito radente statico è un’incognita dinamica
(cioè è una forza incognita a priori); il suo valore dipende dalle altre forze applicate al punto materiale e può
essere determinato studiando la condizione di statica.
La forza di attrito radente statico non può però assumere un valore arbitrariamente grande. Il valore massimo è
detto forza di stacco. L’intensità della forza di stacco è proporzionale alla forza premente, il cui modulo è sempre
pari a quello della reazione normale del piano di appoggio. Il modulo della forza di stacco può essere scritto
quindi come:
Fmax = µs R
Il coefficiente di proporzionalità dipende dalla natura delle superfici a contatto,1 ed è detto coefficiente di attrito
statico µs. Il valore di µs è invece del tutto indipendente dall’area della superficie di contatto. In base alla
definizione, si vede che [µs] = 1 : il coefficiente di attrito è un numero.
Tornando all’esempio considerato, la condizione di statica implica dunque che:
Fext < µs R
ed essendo R = P = mg:
Fext < µs mg
Forza di attrito radente cinematico.
Superato il valore della forza di stacco, la natura della forza di attrito muta radicalmente. Quando le superfici a
contatto slittano l’una sull’altra, si parla di attrito radente cinematico (o meno propriamente, attrito dinamico).
L’intensità della forza di attrito radente cinematico è proporzionale alla reazione vincolare R del piano di
appoggio:
Fc = µc R
Il coefficiente di proporzionalità µc è detto coefficiente di attrito cinematico. Come nel caso di µs, anche µc
dipende dalla natura delle superfici ed è del tutto indipendente dall’area di contatto. A parità di condizioni, è
sempre minore del coefficiente di attrito statico:
µd < µs
Per questa ragione, se la forza esterna raggiunge il valore della forza di stacco e poi si mantiene costante, il corpo
accelera. Si supponga infatti che, appunto, sia
Fext = µs R
L’equazione della dinamica si scrive:
F ext + Fa + R + P = m a
Proiettando sugli assi:
Fext − Fa = m a
;
R−P=0
µs R − µc R = m a
;
R=P
( µs
− µc ) P = m a ;
a = ( µs − µ c ) g
1
e cioè, dal tipo di materiali e dalla lavorazione; dalla presenza di lubrificanti; dalla temperatura; ecc.
Poiché µc < µs , si ha a > 0
Questa circostanza spiega perché, ad esempio, dopo aver determinato la condizione di stacco di un oggetto
pesante, come un armadio, capiti di sentirlo “scappar via”, al punto che se non si diminuisce la spinta si rischia di
perdere l’appoggio e di vederlo fermarsi nuovamente.
Attrito nel moto di rotolamento
Nel loro moto, i corpi estesi possono sia traslare che ruotare. Il moto di rotolamento è una particolare combinazione di
traslazione e rotazione.
Per convenienza, anziché mostrare una ruota, in figura è stato rappresentato un corpo sfaccettato; ma si può
immaginare che, all’aumentare del numero dei lati, questo approssimi sempre meglio un cilindro.
Nel puro rotolamento, il punto di contatto al suolo P è fermo. Dopo la rotazione di un certo angolo, il punto di contatto
cambia (il vertice Q tocca il suolo). Nel caso del cilindro, si deve immaginare che quest’angolo sia infinitesimo.
Quando invece P non è fermo, si ha una combinazione di traslazione (del tratto ∆s) e rotazione: il corpo slitta.
Siccome P non si muove, si capisce che, nel moto di puro rotolamento, l’attrito in P è sempre radente statico.2 Nel caso
r
in cui invece il corpo slitta, l’attrito è radente cinematico. La direzione della forza Fa è in ogni caso parallela al piano,
il verso opposto a quello di avanzamento.
Accelerazione e frenata di un’autovettura
La meccanica di un autoveicolo è molto complessa. Tuttavia, è possibile determinare la massima accelerazione
possibile (in partenza o in frenata) in base a semplici considerazioni riguardanti la forza di attrito.
Si consideri innanzitutto il caso della frenata. Le uniche forze esterne che agiscono su un autoveicolo sono il peso, la
reazione normale del piano stradale, l’attrito radente al contatto tra gomme e asfalto. Se durante la frenata le gomme
non slittano, l’attrito è radente statico.
2
Attenzione a non confondere l’attrito radente statico in P, sempre presente nel puro rotolamento, con l’attrito volvente,
dovuto alla deformazione degli oggetti alla superficie di contatto al suolo.
Nell’approssimazione di punto materiale, queste sono le uniche forze di cui si deve tenere conto per determinare la
cinematica. Esistono naturalmente altre forze in gioco, esercitate tra i vari dettagli meccanici dell’auto. Si tratta tuttavia
di forze interne, a due a due uguali e opposte e quindi a somma zero. In definitiva, il diagramma di corpo libero è
mostrato in figura.
Costruzione del diagramma di corpo libero, per la frenata di un’autovettura, nell’approssimazione di punto
materiale. a) sono rilevanti solo le forze esterne; b) è inessenziale la forma dell’oggetto; c) non è importante il punto
di applicazione, e si possono considerare l’attrito e la reazione totali, senza curarsi della ripartizione sugli assi.
La corrispondente equazione della dinamica si scrive:
Fa + R + P = m a
Proiettando sugli assi:
− Fa = m a
R−P=0
→
Fa
a=−
m
R = P
Il valore di Fa è determinato dalla pressione del piede sul pedale del freno; in tal modo è possibile modulare la frenata.
Tuttavia, il massimo valore che |a| può assumere (la frenata più brusca possibile) dipende esclusivamente dalle gomme
e dal manto stradale. Infatti, quando Fa raggiunge il suo massimo valore possibile, pari a Fmax, si ha:
a =
Fmax µ s R µ s P µ s mg
=
=
=
= µs g
m
m
m
m
Questo risultato sfata la convinzione, piuttosto comune, secondo la quale le autovetture più pesanti frenino meglio. E’
facile individuare un contro esempio convincente: le autovetture sportive (ad esempio, quelle di F1) sono molto più
leggere delle auto commerciali, ma permettono decelerazioni nettamente più brusche. Ciò è dovuto non tanto alla
scelta dei pattini dei freni, o di altri dettagli meccanici, quanto alla scelta delle gomme, caratterizzate da valori di µs
decisamente alti (come noto, a spesa della durata decisamente breve!)
Appare a prima vista sorprendente che anche la massima accelerazione in partenza sia determinata solo da µs . Il
motore non conta nulla?
Per comprendere meglio la situazione, si può fare riferimento a una situazione molto più semplice, che presenta
tuttavia strette attinenze a quella considerata. Un blocco di massa m è tratto da una molla, il cui secondo estremo è
ancorato alla massa m’. Quest’ultima poggia su un piano scabro. La molla gioca in questo caso il ruolo del “motore”
che mette in movimento m; mentre il contatto di m’ al suolo è analogo al contatto delle gomme sull’asfalto.
Per aumentare l’accelerazione a della massa m, è possibile tendere maggiormente la molla. Tuttavia, se si esagera, la
massa m’ slitterà determinando l’effetto opposto. Qual è il massimo valore che la forza elastica può assumere?
Schema di principio per illustrare il ruolo del motore di
m (la molla) e del contatto al suolo (la massa m’,
soggetta ad attrito radente)
Principio di azione e reazione: la molla media
l’interazione (attrattiva) tra m e m’; dunque le forze
applicate a m e m’ sono uguali e opposte. Si tratta di
forze interne.
Diagramma di corpo libero della massa m’
Diagramma equivalente per la massa m: la forza motrice
r
è sempre uguale a Fa
Con riferimento alla figura, si vede che:
a) per il principio di azione e reazione, le forze esercitate ai due capi della molla sono uguali in modulo e opposte in
verso:
r
r
Fe = − F'e
→
F’e = Fe
b) l’equazione della statica, applicata alla massa m’, si scrive:
F 'e + Fa + R + P = 0
che proiettata sull’asse orizzontale, diventa:
-F’e + Fa = 0
→
F’e = Fa
c) combinando i risultati in a), b), si ottiene:
Fe = Fa
e, tenendo conto che i vettori sono paralleli e concordi:
Fe = Fa
Questo risultato mostra che la forza motrice applicata a m è sempre uguale alla forza F a , giustificando il diagramma
semplificato dell’ultimo disegno.
In base a questa premessa, si può facilmente rispondere alla domanda lasciata in sospeso: il massimo valore che la
forza elastica può assumere è pari alla forza di stacco Fmax che caratterizza l’attrito di m’.
Tornando al caso dell’auto in accelerazione, il diagramma semplificato è quello riportato in figura (per il caso di
trazione posteriore).
La massima accelerazione in partenza sarà ottenuta in corrispondenza al massimo possibile valore della forza di attrito
radente statico; quindi, quando la proiezione su un asse orizzontale della II legge di Newton assuma la forma:
Fmax = m a
da cui:
a=
Fmax µ s P
=
= µs g
m
m
Come si vede, in modulo la massima decelerazione e la massima accelerazione possibili sono uguali.
Tornando all’esempio delle auto di F1, questo risultato giustifica il modo in cui i piloti (o i sistemi automatici)
gestiscono la fase di partenza. Prima del rilascio della frizione, il motore è tenuto al massimo dei giri; ma subito dopo
l’attacco, il pedale dell’acceleratore viene sollevato per evitare il pattinamento delle ruote. In regime di pattinamento,
l’accelerazione massima sarebbe determinata dall’attrito radente cinematico e pari a µc g. Si tratta di una situazione
sfavorevole, perché µc < µs
Infine, si noti che il modello delle masse m, m’ collegate dalla molla descrive molto bene altre situazioni interessanti;
per esempio, m può rappresentare un corridore, m’ il piede d’appoggio e la molla la massa muscolare in trazione.
Piano inclinato in presenza di attrito
Si consideri la situazione rappresentata in fig. 1. Abbiamo un corpo di massa m, poggiato su un piano scabro. Il piano è
dotato di una cerniera che permette di modificare a piacimento l’angolo di inclinazione θ.
y
r
N
r
Fa
r
P
θ
x
Fig. 1. Diagramma di corpo libero per una massa
poggiata su un piano scabro.
Nella condizione iniziale, la massa m è ferma e il piano è orizzontale. Lentamente, si inclina il piano e, per piccoli
valori di θ, certamente il corpo rimane fermo. La condizione di statica è determinata, a partire dal diagramma di corpo
libero mostrato in figura, dall’equazione:
r
r r
Fa + P + N = 0
eq.1
che proiettata sugli assi in figura, dà:
− Fa + P sen θ = 0
N − P cos θ = 0
In questa condizione, Fa è un’incognita dinamica. Il suo valore è semplicemente fissato dalla prima delle due equazioni
scalari (curva nera nel diagramma in fig. 3):
Fa = P sen θ
eq. 2
e quindi, Fa aumenta all’aumentare dell’inclinazione θ. La reazione vincolare del piano, intanto, si calcola a partire
dalla seconda equazione e vale:
N = P cos θ
Tuttavia, Fa non può eccedere il valore massimo, pari alla forza di stacco data dalla relazione:
Fmax = µ s N = µ s P cos θ
Quindi, quando l’angolo θ raggiunge un certo valore critico θs , il corpo inizia a scivolare. Questo valore si determina
imponendo che sia Fa = Fmax e, dunque:
P sen θs = µs P cos θs
tg θs = µs
Questa equazione dà un’indicazione su come misurare µs: basta trovare sperimentalmente l’angolo per il quale il corpo
si mette in movimento.
Dal momento che il corpo non è più fermo, l’eq.1 (equazione della statica) cessa di valere, perché ci si trova in
condizioni dinamiche. Vale invece l’equazione:
r
r r
r
Fa + P + N = m a
eq.3
Il diagramma di corpo libero è apparentemente uguale a prima, ma ora la somma dei tre vettori forza non è più nulla.
Un esempio grafico che mostra questo effetto è riportato in fig.2.
r
N
r
Fa
r
P
r
N
r
Fa
Fig.2. Nel primo diagramma, la somma dei tre vettori è
nulla; nel secondo, si annulla solo la componente
perpendicolare al piano.
r
P
L’eq.3, proiettata sugli assi, dà le equazioni scalari:
− Fa + P sen θ = m a x
N − P cos θ = 0
In queste equazioni, compaiono come incognite ax e N. Il valore di Fa, infatti, non va più considerato incognito: in
regime cinematico, l’attrito è determinato dalle proprietà delle superfici a contatto, secondo la relazione:
Fa = µ c N
Ricavato il valore di N dalla seconda equazione, si trova Fa:
Fa = µc N = µ c P cos θ
eq. 4
Il grafico di Fa in questo regime è rappresentato dalla curva a tratto blu in fig.3.
Si noti che, in θ = θs, Fa è discontinua, passando dal valore di attrito statico Fa = Fs max = µs P cos θs al valore di attrito
cinematico Fa = µ c P cos θs . Il valore di attrito cinematico è sempre più basso, siccome del tutto in generale si ha
µs > µ c .
Nelle condizioni appena descritte, il corpo scivola con accelerazione ax data da:
m a x = P sen θ − Fa
ax =
P
F
sen θ − a
m
m
ax =
P sen θ
µ P cos θ
− c
m
m
e infine:
a x = g sen θ − µ c g cos θ
eq. 5
Se µc è piccolo, questa accelerazione è molto prossima a quella che si trova nello slittamento sul piano inclinato senza
attrito ( a x = g sen θ ) . Altrimenti, il moto è comunque accelerato, cioè ax > 0 . Questa osservazione è intuitivamente
ovvia (il corpo è stato appena messo in moto!) e può essere verificata analiticamente, riscrivendo l’espressione di ax:
a x = g cos θ (tg θ − µc ) > g cos θ (tg θc − µc ) = g cos θ (µs − µ c ) > 0
Visto che in queste condizioni il corpo accelera, come è possibile ottenere uno slittamento a velocità costante?
Si deve diminuire gradualmente θ : l’accelerazione diventa via via minore, come si vede dall’eq. 5. L’accelerazione si
annulla quando l’angolo è pari a θc , dato dall’equazione:
0 = g sen θc − µ c g cos θc
tg θc = µ c
L'angolo θc è dunque più piccolo di θs.
Fissato il piano inclinato esattamente a questo angolo, il corpo si muoverà a velocità costante. Naturalmente, se
l’angolo diminuisce ancora, l’accelerazione diventa negativa. Il corpo frena: basterà aspettare un po’, e lo ritroveremo
in condizioni di statica.
E’ interessante, infine, notare che, quando l’inclinazione è stata diminuita, l’attrito è rimasto pur sempre cinematico,
anche al di sotto dell’angolo θs (quindi, vale l’eq. 4). Il grafico di Fa in queste condizioni è riportato in rosso in fig. 3.
La fig.3 mostra questa particolarità. In base alla discussione precedente, si vede che l’attrito non dipende solo dal
valore dell’angolo, ma anche da come si è arrivati a quel valore di angolo (la “storia” dell’esperimento). In termini
tecnici, questo comportamento è descritto dicendo che il sistema presenta isteresi, o che ha un comportamento
isteretico.
Fig.3. In condizioni di statica, la forza di attrito aumenta man mano che il piano è più inclinato (curva nera).
Raggiunto il valore della forza di stacco, l’attrito diminuisce bruscamente (freccia nera rivolta verso il basso) e si
entra nel regime cinematico 1 (curva blu). Si noti che, per θ = 90°, l’attrito cinematico è nullo: in queste condizioni
il piano è verticale e non c’è forza normale. Se si torna a diminuire l’angolo di inclinazione, il corpo resta soggetto
ad accelerazione positiva anche al di sotto dell’angolo θs (curva rossa, regime cinematico 2). All’angolo θc , il corpo
ha accelerazione nulla.3 Diminuendo ancora l’angolo (curva verde, regime cinematico 3), l’accelerazione diventa
negativa: il corpo frena. Dopo un po’ di tempo sarà fermo e si tornerà bruscamente sulla curva nera (freccia verticale
verde).
Si noti che l’istante in cui il corpo si ferma dipende da quanto si stava muovendo velocemente: quindi la posizione
della freccia verde non si può determinare senza avere le condizioni iniziali del moto.
Alcuni valori del coefficiente di attrito radente
Superfici
Legno – legno
Acciaio – acciaio
Acciaio – acciaio lubrificato
Acciaio – teflon
Gomma – asfalto
Gomma – asfalto (bagnato)
3
µs
µc
0.5
0.8
0.1
0.04
0.7
0.4
0.3
0.4
0.05
0.04
0.5
0.2
Considerando che tg θc = µc ; Fa = P sen θ (statica, curva nera); Fa = µc P cos θ (dinamica, curva rossa); è facile vedere
µc
che, nella condizione ax = 0 , curva nera e rossa si intersecano al valore Fa =
P
1 + µ c2