s_100223

STATISTICA E CALCOLO DELLE PROB.
Martedì 23 febbraio 2010
Prof. Cesare Svelto
Tempo a disposizione 1 ora 30 min
Primo appello AA 2009/2010
Aula Vs.8 ore 12.30
Cognome e nome: ___________________________________ _____________________
Matricola e firma __ __ __ __ __ __
(stampatello)
_____________________(firma leggibile)
Esercizi svolti (almeno parzialmente): 1 2 3 4 (6+9+8+10 = 33p)
(crocettare)
N.B. gli esercizi non crocettati non saranno corretti; quelli crocettati ma neanche iniziati comporteranno una
penalità.
SOLUZIONI
Esercizio 1 (tempo stimato 15 m)
(svolgere su questo foglio e sul retro)
1) Si intende fare uno studio statistico sul numero di studenti che si iscrivono ad un corso di laurea. Negli
ultimi 14 anni gli iscritti x sono stati:
x = 137, 142, 95, 134, 112, 121, 111, 138, 159, 140, 146, 107, 119, 103.
1a) Si calcolino media e deviazione standard campionaria.
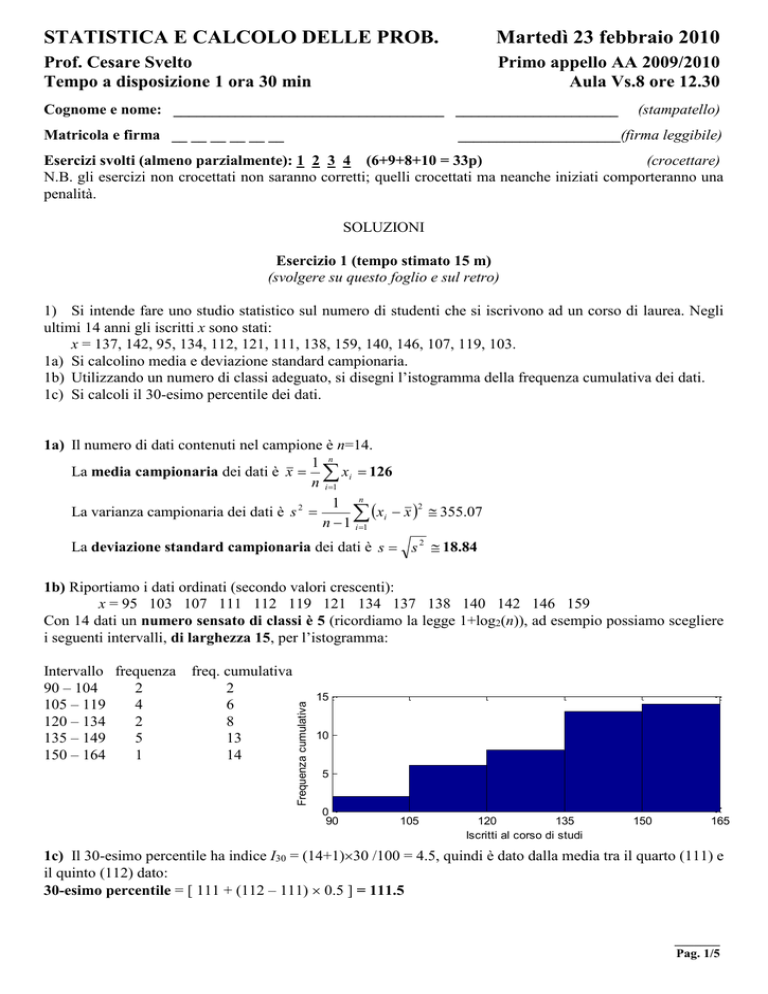
1b) Utilizzando un numero di classi adeguato, si disegni l’istogramma della frequenza cumulativa dei dati.
1c) Si calcoli il 30-esimo percentile dei dati.
1a) Il numero di dati contenuti nel campione è n=14.
1 n
La media campionaria dei dati è x   xi  126
n i 1
1 n
xi  x 2  355.07
La varianza campionaria dei dati è s 2 

n  1 i 1
La deviazione standard campionaria dei dati è s  s 2  18.84
Intervallo frequenza freq. cumulativa
90 – 104
2
2
105 – 119
4
6
120 – 134
2
8
135 – 149
5
13
150 – 164
1
14
Frequenza cumulativa
1b) Riportiamo i dati ordinati (secondo valori crescenti):
x = 95 103 107 111 112 119 121 134 137 138 140 142 146 159
Con 14 dati un numero sensato di classi è 5 (ricordiamo la legge 1+log2(n)), ad esempio possiamo scegliere
i seguenti intervalli, di larghezza 15, per l’istogramma:
15
10
5
0
90
105
120
135
Iscritti al corso di studi
150
165
1c) Il 30-esimo percentile ha indice I30 = (14+1)30 /100 = 4.5, quindi è dato dalla media tra il quarto (111) e
il quinto (112) dato:
30-esimo percentile = [ 111 + (112 – 111)  0.5 ] = 111.5
_______
Pag. 1/5
Esercizio 2 (25 minuti)
(svolgere su questo foglio e sul retro)
2a)
2b)
2c)
2d)
Il tempo richiesto per abbattere un albero ha valor medio 10 minuti e deviazione standard 5 minuti. Il
tempo per spostarsi da un albero al successivo ha valor medio 2 minuti e varianza 0.9 min2. Si calcoli la
probabilità di abbattere un intero bosco di 100 alberi in meno di 1250 minuti.
In quel bosco un albero su 5 ha una malattia alla corteccia, quanto vale la probabilità di trovare meno di
2 alberi malati su 10 esaminati?
Alla base di un albero si trova un formicaio, da cui esce mediamente una formica ogni 6 s. Quanto vale
la probabilità di vedere uscire esattamente 12 formiche in un minuto? Si motivi la risposta.
Si descriva brevemente come è possibile calcolare una probabilità tramite approssimazione normale.
2a) La variabile casuale “tempo totale” T è data dalla somma dei tempi necessari ad abbattere 100 alberi con
i tempi per spostarsi 99 volte da un albero al successivo:
T= 100TA + 99 TS
Per il teorema del limite centrale la distribuzione di probabilità di T è all’incirca normale, con valor medio e
varianza pari a
  100 A  99 B  1198 min
 2  100 A2  99 B2  2589 min2 da cui   50.9 min
Calcoliamo quindi la probabilità che T sia minore di 1250 minuti per standardizzazione:
1250   
1250  1198 


P(T<1250 min) = P z 
  P z 
  P( z  1.02)  84.6 %

50.9




2b) Dato che ogni prova è un processo di Bernoulli (ogni albero è o non è malato), le prove sono
indipendenti e la probabilità di successo in ogni prova è costante, la probabilità di x alberi malati su n alberi
segue la distribuzione binomiale, con probabilità di successo p =0.2 (uno su 5 è malato):
n
 n
P(x<2) = P( x  0)  P( x  1)    p 0 (1  p) n  0    p1 (1  p) n 1  10.7%  26.8%  37.5 %
0
1
2c) Questo fenomeno segue una distribuzione di probabilità poissoniana. Infatti il singolo evento “uscita di
una formica” è un processo di Bernoulli, che possiamo in prima approssimazione ritenere scorrelato (non si
considerano uscite di formiche in gruppo), con un numero altissimo di uscite possibili ed una probabilità
istantanea di uscita molto bassa.
e   x
,
x  0,1,2...
La funzione di probabilità di una variabile poissoniana X vale f ( x) 
x!
il suo valor medio vale  e la sua varianza vale 2 = .
Il valor medio in questo caso vale  =  = 1 /(6 s) × 60 s = 10
La probabilità che in 1 minuto escano esattamente x = 12 formiche vale quindi
e   x e 101012

 9.5 %
P(x=12) =
x!
12!
2d) Si vedano le dispense del corso.
_______
Pag. 2/5
Esercizio 3 (25 minuti)
(svolgere su questo foglio e sul retro)
3) Ci viene richiesto di verificare la resistenza alla trazione di un modello di fune d’acciaio. Il produttore
dichiara una tensione di rottura media corrispondente a un peso di 100 kg. Portiamo quindi alla rottura 11
funi, misurando un valor medio di 96.6 kg e una deviazione standard campionaria di 5 kg.
3a) Si effettui un test statistico al fine di verificare la resistenza del modello di fune, con livello di
significatività dell’1%.
3b) Si calcoli il valore P del test.
3c) Il produttore vorrebbe garantire un valore di resistenza minima per quel modello di fune. Ci chiede che
valore potrebbe indicare (come peso) in modo che al più 1 fune su 1000 non rispetti le specifiche. Si
descrivano le ipotesi fatte per effettuare il calcolo e si commenti il procedimento adottato.
3a) Si tratta di un test t, in quanto dobbiamo stimare il valor medio di una popolazione con varianza ignota. Il
numero di gradi di libertà  = n – 1 = 10. La deviazione standard campionaria vale 5 kg.
Effettuiamo quindi un test t.
1. Il parametro di interesse è la resistenza alla trazione
2. H0:  = 100 kg
3. H1:  < 100 kg (il test è a un solo lato, in quanto vogliamo dimostrare che la resistenza è minore di
quella dichiarata)
4. Livello di significatività richiesto  = 0.01
5. La statistica di test è la statistica t: t 0 
X  X 

sX
s/ n
6. Rifiutiamo H0 se t0 < - t,10 = -2.764 (questo risultato si ricava dalla tabella dei punti percentuale della
distribuzione t, con  = 10 e  = 0.01)
7. Calcoliamo quindi t0, t 0 
X   X   96.6  100


 2.25
sX
s/ n
5 / 11
8. Conclusione: non possiamo rifiutare l’ipotesi nulla con livello di significatività 0.01.
Dunque la resistenza della fune è verificata con  = 0.01.
3b) Il valore P di un test statistico è il più piccolo livello di significatività  che porterebbe a rifiutare
l’ipotesi nulla H0.
In questo caso dalla tabella t si ricava che il valore di  che fornisce t,10  2.25 è circa 0.025, per cui il valore
P in questo caso vale 2.5 %.
3c) I dati che abbiamo a disposizione sono la media e la varianza campionaria stimate su 11 misure. Per dare
una stima del valore richiesto supponiamo che la variabile in gioco segua una distribuzione normale, con
valore medio e varianza pari alle nostre stime. Dalla tabella della distribuzione cumulativa ricaviamo
Z= -3.09 in corrispondenza alla probabilità dello 0.1 % (1 su 1000). Per cui il valore richiesto vale
X = Z      3.09  5  96.6 kg  81.15 kg
Per ottenere un valore più affidabile sarebbero richieste molte più misure, in modo da valutare meglio sia il
valor medio e la varianza, sia anche la distribuzione di probabilità (che è stata supposta normale).
_______
Pag. 3/5
Esercizio 4 (25 minuti)
(svolgere su questo foglio e sul retro)
4) Si vuole misurare la potenza elettrica P dissipata su un resistore di valore nominale R=100  con PDF
triangolare di 2 %. Con un voltmetro digitale ideale, a 2½ cifre e con fondo scala 20 V, si legge ai capi del
resistore una tensione di 12.1 V.
4a) Si ricavi la misura indiretta, con l’incertezza tipo espressa in notazione compatta, per la potenza P.
4b) Se una seconda misurazione indipendente della stessa potenza, eseguita con un metodo calorimetrico, ha
fornito il valore Pcal=150050 mW con un livello di confidenza del 99.7 %, si valuti la compatibilità tra le
misure P e Pcal.
4c) Si ricavi la miglior stima della potenza elettrica, esprimendone l’incertezza con un fattore di copertura
k=2.
4a) L’equazione della misura è P=V2/R, relazione funzionale espressa come produttoria generalizzata delle
variabili di ingresso V e R.
Il valore della potenza elettrica, ottenuta indirettamente da V e I, è P=(12.1 V)2/(100 )=1.4641 W.
L’incertezza di V, data la risoluzione del voltmetro V=0.1 V, è una incertezza di quantizzazione pari a
u(V)=V/ 12 =29 mV. L’incertezza relativa è ur(V)=u(V)/V=2.4×10-3.
L’incertezza di R, data la PDF triangolare di piena larghezza R=2%100 =4  è una incertezza di
categoria B pari a u(R)=R/ 24 =0.82 . L’incertezza relativa è ur(R)=u(R)/R=8.2×10-3.
L’incertezza relativa di P è ur(P)= 4ur2 (V )  2r ( R) =9.5×10-3. e la corrispondente incertezza assoluta è
u(P)=ur(P)P=0.014 W=14 mW=1.4×10-2 W.
La misura indiretta è dunque P=1.464(14) W.
4b) Nella
misura
con
il
calorimetro,
il
valore
è
Pcal=1.5 W
e
l’incertezza
è
-2
u(Pcal)=50 mW/3=17 mW=1.7×10 W, essendo k=3 per P=99.7 %.
La compatibilità tra le due misure di potenza, assunte indipendenti, viene valutata con il criterio di
compatibilità standard:
P  Pcal  k u 2 ( P)  u 2 ( Pcal )
che, esprimendo i valori in milliwatt, si può scrivere come
36k
142  172 k21
da cui si ricava
k1.66  le due misure sono compatibili per k=2 e k=3.
4c) La miglior stima della misura si ottiene dalla media pesata delle misure compatibili:
P
P
 2 cal
2
u ( P ) u ( Pcal )
PMP=
=1479 mW
1
1

u 2 ( P ) u 2 ( Pcal )
con una incertezza tipo
_______
Pag. 4/5
u(PMP)=
1
1
1
 2
2
u ( P) u ( Pcal )
=11 mW
e una incertezza estesa U(PMP)=ku(PMP)=2u(PMP)=22 mW.
Infine: PMP=147922 mW con k=2.
_______
Pag. 5/5