Esercizi e problemi sugli atomi idrogenoidi

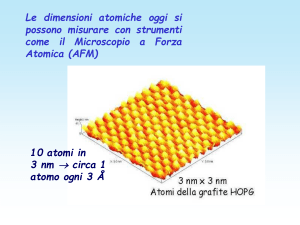
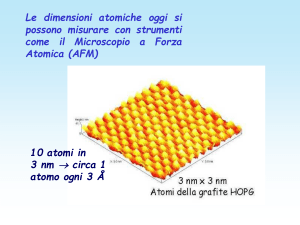
Corso di Laurea in Fisica
Corso di Struttura della Materia
G. Rinaudo - a.a.2001/02
Esercizi e problemi sugli atomi idrogenoidi
* Esercizio 2: Potenziali, livelli energetici e funzioni d’onda radiali dell’elettrone in un
potenziale coulombiano
a) Calcolare l’energia potenziale coulombiana di un elettrone nell’atomo di idrogeno e i
livelli energetici corrispondenti a n=1, 2, 3 e riportarli in un grafico in funzione della
distanza r dal nucleo. Individuare sul grafico i “punti di inversione” per il caso di
numero quantico di momento angolare l=0
b) Calcolare e riportare in un grafico le funzioni d’onda radiali u(r)(*) dell’elettrone
dell’atomo di idrogeno corrispondenti a n=1, 2, 3 ed l=0. Individuare sul grafico i nodi
delle funzioni e i flessi che non corrispondono ai nodi.
c) Calcolare il “potenziale effettivo”, somma dell’energia potenziale coulombiana e del
termine di barriera centrifuga, di un elettrone nell’atomo di idrogeno per gli stati di
numero quantico di momento angolare l=1 e 2 e riportarli in grafici separati in funzione
della distanza r dal nucleo. Calcolare i livelli energetici corrispondenti a n= 2 e 3 e
riportarli sui due grafici. Individuare sugli stessi grafici i “punti di inversione.
b) Calcolare e riportare in un grafico le funzioni d’onda radiali u(r)(*) dell’elettrone
dell’atomo di idrogeno corrispondenti a n=2 per tutti i valori permessi di l. Ripetere il
calcolo per n=3. Individuare sui grafici i nodi delle funzioni e i flessi che non
corrispondono ai nodi.
__________
(*)
Alonso esempio 3.5
Impostazione del calcolo
è Assi, sistema di riferimento, costanti, relazioni importanti
z
m = massa dell’elettrone
E = energia totale (cinetica + potenziale)
Ep = energia potenziale, Ep = -e2 /2r
EL = barriera di potenziale centrifugo
EL =
2
⟨L ⟩
2mr
2
=
l (l + 1) h
θ
2
r
2mr 2
y
Eeff = Ep + EL = potenziale “effettivo”
ϕ
x
1
è Richiami teorici
In presenza di un potenziale centrale, che dipende cioè dal solo modulo della distanza r, come è
quello degli atomi idrogenoidi, conviene esprimere l’hamiltoniana H e la funzione d’onda ψ
dell’elettrone, soluzione dell’equazione di Schroedinger, in coordinate sferiche (r, θ, ϕ), indicate in
figura. In queste coordinate, H si può scrivere nel seguente modo:
 p2
L2
Ze 2 
Hψ ( r ,ϑ , ϕ ) =  r +
−
ψ ( r ,ϑ ,ϕ ) = Eψ ( r ,ϑ ,ϕ )
(1)
 2m 2mr 2

r


H è quindi somma di 3 operatori, di cui uno solo, L2 , opera, in modo semplice, sugli angoli θ, ϕ e
uno solo, pr2 , opera su r. In questo modo la funzione d’onda è fattorizzabile, cioè si può scrivere
come prodotto di una funzione R(r) che dipende solo da r e una funzione Y(θ, ϕ) che dipende solo
dagli angoli θ, ϕ (Alonso, eq. 3.18):
u ( r ) ml
Y (ϑ , ϕ )
(2)
r l
dove abbiamo già espresso la parte radiale della funzione d’onda in termini della funzione u(r) che
permette di semplificare i calcoli successivi. Le funzioni sferiche Yl,m (θ, ϕ) sono autofunzioni di L2 ,
con autovalori associati al numero quantico di momento angolare l:
ψ ( r ,θ ,ϕ ) = R (r )Yl
L2Yl
ml
ml
(ϑ , ϕ ) =
ml
(ϑ , ϕ ) = l (l + 1)h 2Yl
(ϑ , ϕ )
(3)
Sostituendo le eq. 2 e 3 nella 1, e dividendo per la funzione sferica, si ottiene l’equazione a cui deve
soddisfare la funzione u(r) (Alonso, eq. 3.24).
−
h 2 d 2u ( r )  l (l + 1)h 2 Ze 2 
+
−
u( r ) = Eu (r )
 2mr 2

2 m dr 2
r


(4)
Questa equazione ha la tipica espressione che si presenta spesso nelle equazioni di Schroedinger, è
cioè una relazione fra la curvatura della funzione u(r), cioè la sua derivata seconda, e la funzione
stessa. Per vederlo meglio, conviene riscrivere l’equazione nel seguente modo:
d 2u ( r )
dr 2

2m  l (l + 1)h 2 Ze 2
u ( r ) = 2m Eeff − E u( r )
= 2
−
−
E

r
h  2mr 2
h2

(
)
(5)
dove abbiamo chiamato Eeff il potenziale “effettivo”, cioè la somma dell’energia potenziale
coulombiana e del termine di barriera centrifuga. L’eq. 5 mostra chiaramente che la funzione
d’onda
- ha dei flessi, cioè dei punti di curvatura nulla, per quei valori di r in cui u(r) è nulla (“nodi”) ma
anche per quei valori di r in cui Eeff è pari all’energia E, cioè nei punti che, nel moto classico,
avremmo chiamato “punti di inversione,
- la curvatura ha lo stesso segno di u(r) per quei valori di r in cui Eeff > E, mentre ha segno
opposto se Eeff < E,
- la curvatura è elevata, cioè la funzione d’onda varia rapidamente al variare di r, nelle zone in cui
Eeff – E è elevato.
L’equazione 5 si può risolvere analiticamente, le soluzioni per le funzioni fino a n=3 sono date nella
tabella 3.6 di Alonso e Finn e riportate di seguito. Per il calcolo conviene definire la distanza radiale
ridotta, ρ = 2Zr/nao , che è adimensionale, e la costante di normalizzazione C=(Z/ao )3/2 .
2
Nodi:
- per il massimo valore di l permesso, cioè l=n-1, c’è un solo nodo, per r=0;
- per l=n-2, oltre al nodo per r=0, c’è un nodo intermedio, che capita a ρ = 2, r=2ao per u20 e a
ρ= 4, r=6ao per u31 ;
- per l=n-3, oltre al nodo per r=0, ci sono due nodi intermedi nella funzione u30 , che capitano per
3
i valori di ρ che soddisfano l’equazione ρ2 - 6ρ + 6 = 0, ρ = 3 ± 3 , r = ( 3 ± 3 ) .
2
Flessi:
- escludendo i flessi che coincidono con i nodi, si ha un solo flesso per le funzioni d’onda con
Ze 2
;
En
per l>0, i flessi non coincidenti con i nodi sono due, che corrispondono ai valori di r per cui
l=0, che corrisponde al valore di r per cui En =Ep , cioè r =
-
2
En =Eeff =Ep +EL
2
Ze
l (l + 1)( hc)
e si ottengono risolvendo l’equazione En −
+
= 0 . Ponendo
r
2mc 2 r 2
b = l (l + 1)( hc ) 2 / 2 mc2 , si può riscrivere l’equazione come
soluzioni sono r =
Ze 2 ± Z 2 e 4 − 4 En b
2 En
En r 2 − Ze 2 r + b = 0 , le cui
.
Tabella delle funzioni u(r)
2Z
ρ=
r;
nao
3/2
Z 
C =  
 ao 
na
r = o ρ;
2Z
n =1
l =0
u10 ( r ) = 2 C r e − ρ / 2
n=2
l =0
u20 (r ) =
1
n=2
l =1
2 2
1
u21 ( r ) =
C r ρ e− ρ / 2
2 6
n =3
l=0
u30 (r ) =
1
n =3
l =1
n =3
l=2
C r (2 − ρ ) e − ρ / 2
C r (6 − 6 ρ + ρ 2 ) e − ρ / 2
9 3
1
u31 ( r ) =
C r ρ (4 − ρ ) e − ρ / 2
9 6
1
u32 ( r ) =
C r ρ 2 e− ρ / 2
9 30
Calcoli e grafici
Conviene impostare tutti i calcoli e i grafici usando MATEMATICA o anche un semplice foglio
excel. Un esempio per l=0 si trova nel foglio “quant. l=0” del file excel idrogeno.xls e per l=0, 1 e
2 nel foglio “quant. l=0,1,2” dello stesso file.
3
Di seguito riportiamo i grafici e i valori di r nei nodi e nei flessi.
Funzioni d'onda
l =0
14,0
12,0
0
2
4
6
8
r (angstrom)
10
12
u10
10,0
8,0
flesso di u10
6,0
u30
flesso di u30
4,0
nodo di u20
2,0
nodo di u30
0,0
-2,0
nodo di u30
u20
-4,0
flesso di u20
-6,0
-8,0
Energia (eV)
-10,0
0,0
E3
punto di inversione per n=3 E2
-5,0
punto di inversione per n=2
-10,0
punto di inversione per n=1
E1
-15,0
-e2/r
-20,0
Potenziale e livelli energetici
-25,0
-30,0
0,00
2,00
4,00
6,00
r (angstrom)
8,00
10,00
12,00
4
Funzioni d'onda
10,0
0
2
4
n =2; l = 0,1
6
8
r (angstrom)
10
12
u21
5,0
flessi di u21
0,0
u20
-5,0
flesso di u20
Energia (eV)
-10,0
10,0
5,0
0,0
E3
punto di inversione per l=0, n=2
-5,0
E2
punti di inversione per l=1, n=2
-10,0
-15,0
-e2/r
E1
-20,0
Potenziale e livelli energetici
-25,0
-30,0
0,00
2,00
4,00
6,00
8,00
10,00
12,00
r (angstrom)
5
Funzioni d'onda
n =3; l = 0,1,2
10,0
0
2
4
6
8
r (angstrom)
10
12
8,0
6,0
flesso di u30
u32
4,0
flessi di u32
2,0
0,0
u30
-2,0
-4,0
flesso di u21
u31
flesso di u21
-6,0
Energia (eV)
-8,0
10,0
punti di inversione per l=2, n=3
5,0
0,0
E3
E2
-5,0
punti di inversione per l=1, n=3
punto di inversione per l=0, n=3
-10,0
E1
-15,0
-e2/r
-20,0
Potenziale e livelli energetici
-25,0
-30,0
0,00
2,00
4,00
6,00
8,00
10,00
12,00
r (angstrom)
6
Esercizi suggeriti
2.1 Ripetere l’intero calcolo per l’elio (Z=2) ionizzato, He+ e per il litio (Z=3) ionizzato due volte,
Li++
7