4tea problemi 15

PROBLEMI
DI
FISICA AMBIENTALE
-ENERGIA-
ANNO SCOLASTICO 2014-2015
PROF. ING. RICCARDO FANTON
Istituto Tecnico”S.B.Boscardin”
Vicenza
DILATAZIONE TERMICA
1) Una sbarra di acciaio (d= 11 10-6 1/K) è lunga 20 cm alla temperatura di 20°C. Di
quanto si allunga se la sua temperatura sale a 50°C?
[l=0.0066cm]
2) Una finestra ha il vetro (d= 9 10-6 1/K ) di dimensioni 20,0 cm x 30,0 cm quando
si trova ad una temperatura di 10 °C. Di quanto aumenta la sua superficie quando la
sua temperatura raggiunge i 40°C?
[S=0.32 cm2]
3) Calcolare la variazione di volume di una sfera di alluminio (d= 23 10-6 1/K ), di
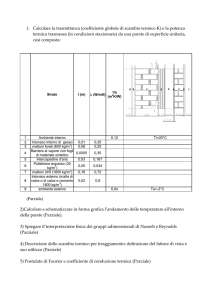
raggio 10,0 cm, quando è riscaldata da 0°C a 100°C.
[V=29 cm3]
CONDUZIONE TERMICA
4) L’acqua fredda, alla temperatura di 15°C, entra in uno scaldaacqua che la porta a
61 °C. Sapendo che uno studente usa 120 kg di acqua calda per fare una lunga
doccia, si calcoli la quantità di calore utilizzata e il costo in energia della doccia se
essa viene pagata 0,25 €/kWh.
[Q=23 MJ]
5) Quando nel corpo umano viene prodotta una quantità eccessiva di energia termica
essa deve essere dispersa affinché la temperatura all’interno del corpo rimanga al
valore normale di 37,0°C. Uno dei meccanismi attivi è la trasmissione per conduzione
attraverso gli strati superficiali di grasso corporeo. Supponiamo che l’energia termica
attraversi 3,0 cm di grasso per raggiungere la cute, che ha un’area totale di 1,7 m 2 e
una temperatura superficiale di 34,0°C. Si calcoli la quantità di energia che raggiunge
la cute in 1,0 h.(conduttività del grasso =0.20 W/mK) [€1.6]
6) Il vetro di una finestra è alto 1.5 m, largo 1.2 m e spesso 4.0 mm. In un’ora escono
5.5 MJ di energia dalla stanza attraverso il vetro. La temperatura della superficie
interna del vetro è di 21 °C e resta costante. Quanto vale la temperatura della superficie
esterna del vetro? (=0.80 W/mK)
[Te=17°C]
7) Un frigorifero ha la superficie interna di area 5,0 m2 ed è rivestito internamente con
un materiale isolante spesso 8,0 cm, la cui conduttività è 0.040 W/mK. La temperatura
interna è mantenuta a 5,0 °C, mentre quella esterna è 25,0°C. Quanto misura il flusso
termico (la potenza) uscente dal frigorifero?
[=50W]
IRRAGGIAMENTO
8) La potenza radiante prodotta dal Sole è di 3.9 1026 W. Approssimando il Sole ad un
corpo nero, =1, si calcoli la temperatura della superficie solare (=5,67.10-8W/m2K4
, raggio del sole r= 6.96 108m)
[S=2.5 10-5m2]
9) Una stufa a legna, spenta, è in una stanza la cui temperatura è 29 °C. Nella stufa
viene acceso un fuoco. La superficie (S=3.50 m2) della stufa si porta, a regime, a 198
°C; l’emissività della stufa è =0.900. Calcola la potenza raggiante totale ( potenza
emessa meno potenza assorbita) generata dalla stufa.
[R=7300W]
10) In una lampada elettrica, il filamento di tungsteno ha la temperatura di 3000°C ed
emette 60 W di potenza raggiante. Supponendo che l’emissività del filamento sia 0.36,
si stimi l’area della superficie del filamento. )
[S=2.5 10-5m2]
CONVEZIONE
11) La parete esterna di un forno è alla temperatura di 50°C. Calcolare il flusso termico
(potenza) dispersa nell’ambiente per unità di superficie, sapendo che l’aria ad una
temperatura di 20°C ha un coefficiente liminare pari a 11.63 W/m2K.
[349W/m2]
12) Un calorifero di acciaio è attraversato da acqua calda che porta le sue pareti ad una
temperatura media di 70°C. Sapendo che è composto da 8 elementi a colonna (area di
una colonna 0.35 m2) e che l’aria nella stanza è mantenuta a 20°C, si calcoli la potenza
termica del calorifero.( Coefficiente liminare dell’aria 7.0 W/m2K).
[980W]
13) Nell’ipotesi che il termosifone dell’esercizio 12) non sia coperto da mobili o
tende, calcolare la potenza trasmessa per irraggiamento. (=0.40=5,67.10-8W/m2K4)
[0.76W]
RESISTENZA TERMICA
14) Calcolare la resistenza termica di pareti di uguale spessore s= 0,25 m e composte
rispettivamente da: laterizio forato =0.43 W/mK, cartongesso =0.21 W/mK,
mattone pieno =0.72 W/mK, cemento armato l=2.3 W/mK. [cart. 1.43W/m2K]
15) La parte vetrata di una finestra a doppi vetri è formata da due lastre di vetro,
entrambe di dimensioni 80 cm*80 cm* 0.40cm, separate da un’intercapedine d’aria di
spessore 1.0 cm. La temperatura della superficie del vetro verso la stanza è di 20°C,
mentre quella della superficie rivolta all’esterno è di 0°C. Quanta potenza passa
attraverso la vetrata? (vetro: v=0.84 W/mK; aria:a=0.080W/mK)
[95W]
16) Data la vetrata dell’esercizio 15), calcolare la resistenza termica e il flusso di calore
considerando che le due temperature indicate siano dell’aria all’interno e all’esterno
della finestra. Si tenga conto della convezione con le superfici effettive del vetro
tramite i coefficienti liminari che valgono rispettivamente h i= 7.0 W/m2K e he=25
W/m2K (condizione stazionaria e velocità dell’aria bassa)
[40W]
TRASMITTANZA
17) Calcolare la trasmittanza della parete indicata in figura 1 adottando le conducibilità
dei materiali riportate nelle tabelle del formulario.
[U=0.240 W/m2K]
18) Calcolare la trasmittanza della parete indicata in figura 2 adottando le conducibilità
dei materiali riportate nelle tabelle del formulario.
LEGENDA
1 – intonaco in gesso s= 1.5 cm
2 – murattura in forati s=8 cm
3+4+5 – pannello in polietilene
espanso s= 6 cm
6 – bimattoni forati a faccia vista
s=25 cm
[U=0.386 W/m2K]
Figura 2
19) Calcolare la trasmittanza della parete indicata in figura 3 adottando le conducibilità
dei materiali riportate nelle tabelle del formulario.
Trattasi di una parete con cappotto esterno.
LEGENDA (strati da sinistra a destra)




Intonaco di calce e cemento s= 1.5 cm
Pannello isolante in polistirene s= 8 cm
Bimattoni forati s= 32 cm
Intonaco di malta e gesso s= 1.5 cm
[U=0.329 W/m2K]
Figura 1
20) Calcolare la trasmittanza del pavimento al piano
terreno (contro terra) indicato dallo schema di figura 4.
LEGENDA
1) piastrelle in ceramica s=0.012 m,
= 1.00 W/mK
2) sottofondo in cemento magro
s=0.040 m, =0.73 W/mK
3) cl.s di perlite e vermiculite
s=0.20m,=0.15 W/mK
Figura 2
4) ghiaione e ciottoli s= 0.40 m, =1.2 W/mK
Il valore del coefficiente liminare discendente è h=5.9 W/mK
[U=0.525 W/m2K]
21) Calcolare la trasmittanza del tetto in legnoindicato nello schema in figura n. 5.
LEGENDA
1) Assito in legno s = 4 cm
2) pannello isolante in polietilene espanso s= 4 cm
3) intercapedine d’aria s=5 cm
4) assito in legno s= 3 cm
Figura 3
5)
tegole
[U=0.673 W/m2K]
in
laterizio
s=
1,5
cm
PONTI TERMICI
22) Stabilisci a quale categoria dell’atlante dei ponti termici puoi assimilare quello
schematizzato nella figura 6. Indicare la possibile correzione.
Figura 7
[SOL006]
Figura 6
23) Stabilisci a quale categoria dell’atlante dei ponti termici puoi assimilare quello
schematizzato nella figura 7. Indicare la possibile correzione. Il pilastro (5) interrompe
una muratura composta da blocchi (2) con bassa trasmittanza (U=0.30W/m2K), le due
tavelle (4) non sono pannelli isolanti.
[PIL003]
24) La parete indicata in figura 8 fa parte di un appartamento e separa una camera e la
sala dall’esterno, che si trova ad una temperatura di – 5°C. L’altezza interna della
parete è di 2,70 m; la muratura, di spessore 40 cm, ha una trasmittanza di 0.40 W/m2K;
le finestre una trasmittanza comprensiva anche dell’effetto schermante delle tapparelle
Uwm=1.75 W/m2K. Definire le trasmittanze lineiche dei ponti termici costituiti dai
pilastri (lato =30 cm) e dai cordoli (s= 30 cm) nell’ipotesi che siano del tipo indicato
in
figura
9
e
calcolare
la
potenza
dispersa
dalla
parete.
Figura 8
Figura 9 –cordolo e pilastro tipo
[530.8 W]
25) l’unità immobiliare indicata in figura 10, è collegata con l’esterno dalla sola parete
cerchiata in rosso.
Figura 10 – pianta del miniappartamento
Figura 11 – sezione sul balcone
La muratura portante è del tipo analizzato nell’esercizio 19 ( vedi figura 11), quindi ha
trasmittanza:
U= 0.329 W/m2K
Le finestre hanno una trasmittanza fornita dal costruttore e comprendente l’effetto
degli scuri:
U wm= 1.05 W/m2K
Determinare il coefficiente del ponte termico del cordolo del balcone e calcolare la
potenza termica dispersa verso l’esterno qundo T= 25°C.LTR=0.43m, s=0.25 m
[559W]
TRASMITTANZA INFISSI
26) Dato il serramento schematizzato in figura 12)
trovare la sua trasmittanza Uw e la trasmittanza del
serramento più la tapparella: U wm.
Figura 12 b – finestra sezione
Lo spessore frontale
delle parti in legno è di
10 cm mentre quello
trasversale è di 12 cm.
Il telaio è in legno di
Pino e i due vetri hanno Figura 12 a) prospetto della finestra
spessore 6 mm, mentre
il distanziatore è largo 1.0 cm. La resistenza
dell’intercapedine di aria è R=0.130 m2K/W (UNI
10071-1 app.C). Dal prospetto E1 di pag.17 del
formulario risulta che la trasmittanza lineica di un
distanziatore del tipo in esame vale : g=0.06 W/mK
[Uwm=2.21 W/m2K]
27) Dato il serramento schematizzato in figura 13) trovare la sua trasmittanza U w e la
trsmittanza del serramento più la tapparella: U wm.
Figura 13 – portafinestra con telaio in PVC
Lo spessore frontale delle parti in PVC è di 9.5 cm,
mentre quello trasversale è di 10 cm. I due vetri
hanno spessore 4 mm, mentre il distanziatore è largo
0.6 cm. La conduttanza del telaio in PVC fornita dal costruttore è Uf=0.75 W/m2K. La
resistenza dell’intercapedine di aria è R=0.130 m2K/W (UNI 10071-1 app.C). Dal
prospetto E1 di pag.17 del formulario risulta che la trasmittanza lineica di un
distanziatore del tipo in esame vale : g=0.06 W/mK
[Uwm=2.26 W/m2K]
28) Il serramento di un abbaino ha le dimensioni indicate in figura 14.
Figura 14 - abbaino
Il serramento ha il telaio in legno di abete di
spessore 12 cm, è dotato nello stato attuale
di un vetro singolo di spessore 4 mm. A
seguito di una ristrutturazione si vuole
riqualificare il serramento senza sostituirlo,
ma cambiando il vetro singolo con un vetro
triplo (4-12-4-12-4)mm. Calcolare la
trasmittanza termica del serramento prima e
dopo la sostituzione dei vetri. La resistenza
dell’intercapedine di aria è R=0.130 m2K/W
(UNI 10071-1 app.C). Dal prospetto E1 di
pag.17 del formulario risulta che la
trasmittanza lineica di un distanziatore del
tipo in esame vale g=0.06 W/mK.
[Uw=2.31W/m2K]
29)Dato il serramento schematizzato in figura 15) trovare la sua trasmittanza U w.
Si tratta di una porta blindata con
intercapedine non isolata. Il contorno
fisso è in profilati di acciaio di dimensioni
5.00 cm frontale e 8.5 cm in larghezza ; lo
spessore dei profilati laterali e delle
piastre di rinforzo è di 2,0 mm. I profilati
laterali contengono un riempimento di
poliuretano espanso. La resistenza
dell’intercapedine di aria è R=0.130
m2K/W (UNI 10071-1 app.C). Il valore
stimato della trasmittanza lineica di una
distanza del tipo in esame vale : g=0.10
W/mK
I pannelli i esterni sono in legno di pino.
Ricalcolarla poi inserendo un pannello
isolante in poliuretano espanso di
spessore 5 cm tra i pannelli d’acciaio riducendo l’intercapedine d’aria a 2 cm.
Figura 15 – schema porta blindata
[Uw=1.07 W/m2K]
CALCOLO DEI CONSUMI ENERGETICI DI UN EDIFICIO
30) L’unità immobiliare in figura 16 è la dependance di un edificio più complesso a
cui è legata dalla parete sud.
N
Figura 16 - Miniappartamento
Si tratta di una porzione di fabbricato ad un solo piano con un’altezza interna media di
2.70 m. Le pareti sono costruite con muratura del tipo analizzato nell’es.19 con
U=0.329 W/m2K, il pavimento contro terra come quello studiato nell’es.20 con
U=0.525 W/m2K e il tetto inclinato come quello presente nella scheda n. 3 della
dispensa con U= 0.772 W/m2K. Le finestre sono in legno con tapparelle come
nell’es.26 con Uwm=2.21 W/m2K, la porta blindata (1,00m *2.15 m) è del tipo
analizzato nell’es.29 con U w=1.07 W/m2K. La finestra del soggiorno misura 1.50m
*1.40m, le due della camera 1.20m * 1.40m, quella del bagno 0.70m *1.40m. La parete
a sud separa l’u.i. da una zona alla stessa temperatura interna e pertanto non disperde.
Il cordolo tra tetto e pareti è assimilabile a quello studiato nell’es.22 con
oi=0.53W/mK. Si calcolino:
 Il coefficiente di dispersione per trasmissione dell’unità immobiliare, H t
 Il flusso termico attraverso l’involucro se soggetto ad un salto termico tra interno
ed esterno di 25°C.
[2.48 kW]
31) Considerando i dati dell’es.30, si calcolino il coefficiente termico di dispersione
per ventilazione dell’unità immobiliare, il flusso termico disperso per ventilazione e il
flusso termico totale.
[2.90 kW]
32) Il miniappartamento di fig.18 appartiene ad un piccolo condominio in cui si trova
al piano terra. (trasmittanza pavimento : Uo=0.31 W/m2K)
Figura 19 – sezione muratura
Legenda
Figura 18 – pianta monolocale

Intonaci in malta di c.to
s=1.5 cm
 Tavelle s = 5.5 cm
 Polistirolo espanso s=8 cm
 Mattoni semipieni s=16.5
cm
La parete nord lo separa da un ambiente riscaldato alla stessa temperatura come pure
il soffitto. La parete ovest è a contatto con il vano scala non riscaldato. Le finestre del
soggiorno e della camera sono di dimensioni 1.20m*1.40m, mentre quella del bagno è
di 0.80m*1.40m. Il costruttore certifica per le finestre una trasmittanza comprensiva
anche dell’effetto delle tapparelle U Wm=2.00 W/m2K. La porta blindata ha dimensioni
1.10m*2.15m e il costruttore certifica una trasmittanza U=1.50 W/m2K. Le pareti sono
del tipo indicato in fig.19. Non sono presenti ponti termici significativi. Il salto termico
interno-esterno è di 25°C.Calcola:
- Il coefficiente di dispersione per trasmissione dell’unità immobiliare, H t
- Il flusso termico attraverso l’involucro
- il coefficiente termico di dispersione per ventilazione dell’unità immobiliare
- il flusso termico disperso per ventilazione
- il flusso termico totale.
[1.46 kW]
33) Calcolare l’energia dispersa durante l’intera stagione invernale dall’involucro
studiato nell’es.30 (Ht=99.1 W/K, HV=15.8 W/K) nell’ipotesi che sia ubicato a
Creazzo (GG1=2510, zona E) oppure a Montechio Maggiore (GG2=2356, zona E)
[M.M. 6921 kWh]
34) Calcolare l’energia dispersa durante l’intera stagione invernale dall’involucro
con Ht=37.7 W/K, Hu=3.14 W/K, HV=18.1 W/K nell’ipotesi che sia ubicato a Vicenza
(GG1=2371, zona E) oppure ad Asiago (GG2=4163, zona F).
[Asiago 5850 kWh]
35) Calcola il fabbisogno di energia per la produzione di ACS dell’unità
immobiliare analizzata nell’es.30. Considerare una temperatura dell’acqua fredda pari
a To=15°C e una temperatura di erogazione Te= 45°C, calore specifico dell’acqua
c=1,162 Wh/kgK, G=365 giorni; Su= 41,4 m2.
[0.0777 m3/giorno]
36) Calcola il fabbisogno di energia per la produzione di ACS dell’unità
immobiliare analizzata nell’es.32. Considerare una temperatura dell’acqua fredda pari
a To=15°C e una temperatura di erogazione Te= 45°C, calore specifico dell’acqua
c=1,162 Wh/kgK, G=365 giorni; Su= 42.8 m2.
[0.0797 m3/giorno]
37) Calcola l’energia totale stagionale dispersa da un’unità immobiliare con Ht=97.7
W/K, HV=17.5 W/K nell’ipotesi che sia ubicato a Creazzo (GG1=2510, zona E) oppure
a Montecchio Maggiore (GG2=2356, zona E), l’energia consumata per l’ACS vale
QW=989 kWh (es.35). Calcola anche il consumo energetico annuale.
[Creazzo QHT= 7929 kWh]
38) Calcola l’energia termica totale stagionale dispersa da un’unità immobiliare con
Ht=37.7 W/K, Hu=3.14 W/K, HV=18.1 W/K nell’ipotesi che sia ubicata a Vicenza
(GG1=2371, zona E) oppure ad Asiago (GG2=4163, zona F), consumo per il
riscaldamento dell’ACS: QW=1014 kWh. Calcola inoltre il consumo energetico
annuale.
[Vicenza QHT = 4367 kWh]
39) Calcola il rendimento medio globale stagionale di un impianto termico costituito
da: radiatori, regolazione on-off, impianto centralizzato con montanti di distribuzione,
caldaia tipo a gas con bruciatore ad aria soffiata.
[0.69]
40) Calcola il rendimento medio globale stagionale di un impianto termico costituito
da: pannelli radianti a pavimento, regolazione elettronica, impianto autonomo,caldaia
a gas a condensazione
[0.83]
41) Calcola l’energia primaria totale degli edifici analizzati negli es.37 e 38
nell’ipotesi che venga utilizzato un impianto del tipo visto nell’es. 39. I dati sono:
- prima unità immobiliare: località Creazzo, QHnd=6940 kWh; località Montecchio
Maggiore, QHnd= 6288 kWh
- seconda unità immobiliare: località Vicenza, Q Hnd=3354 kWh; località Asiago,
QHnd=5850 kWh.
Rendimento globale dell’impianto a radiatori: g=0,69
[Asiago 8478 kWh]
42) Calcola l’energia primaria totale degli edifici analizzati negli es.37 e 38
nell’ipotesi che venga utilizzato un impianto del tipo visto nell’es. 40. I dati sono:
- prima unità immobiliare: località Creazzo, QHnd=6940 kWh; località Montecchio
Maggiore, QHnd= 6288 kWh
- seconda unità immobiliare: località Vicenza, QHnd=3354 kWh; località Asiago,
QHnd=5850 kWh.
Rendimento globale dell’impianto a pannelli radianti: g=0,80 [Vicenza 4192 kWh]
43) Calcola gli indici di prestazione energetica dell’involucro per le quattro
situazioni analizzate nell’es.42). I dati sono indicati nella seguente tabella:
U.I
LOCALITA'
1^
1^
2^
2^
Creazzo
Montecchio Maggiore
Vicenza
Asiago
QHnd
kWh
6940
6288
3354
5850
A
m^2
41.40
41.40
42.80
42.80
[Creazzo 168 kWh/m2anno]
44) Calcola gli indici di prestazione energetica per la climatizzazione invernale per
le quattro situazioni analizzate nell’es.42). I dati sono indicati nella seguente tabella
U.I
1^
1^
2^
2^
LOCALITA'
Creazzo
Montecchio Maggiore
Vicenza
Asiago
QH
kWh
8675
7860
4193
7313
A
m^2
41.40
41.40
42.80
42.80
[Asiago 171 kWh/m2anno]
45) Calcola gli indici di prestazione energetica per la produzione di ACS per le
quattro situazioni analizzate nell’es.42). I dati sono indicati nella seguente tabella:
U.I
1^
2^
LOCALITA'
A
QW
Creazzo e M. Maggiore
Vicenza e Asiago
kWh
989
1014
m^2
41.40
42.80
[2 – 24 kWh/m2anno]
46) Calcola gli indici di prestazione energetica globale per le quattro situazioni
analizzate nell’es.42). I dati sono indicati nella seguente tabella:
U.I
LOCALITA'
1^
1^
2^
2^
Creazzo
Montecchio Maggiore
Vicenza
Asiago
Epacs
Epi
m^2
kWh/m^2anno
24.00
210
24.00
190
24.00
98
24.00
171
[Vicenza 122 kWh/m2anno]
PRODUZIONE DI ANIDRIDE CARBONICA
47) Calcolare le emissioni di gas ad effetto serra in atmosfera (CO 2) degli impianti
delle unità immobiliari i cui valori di indice di prestazione energetica globale (o
primaria) sono stati calcolati nell’es.46.
U.I
1^
1^
2^
2^
LOCALITA'
Epgl
kWh/m^2anno
Creazzo
234
Montecchio Maggiore
214
Vicenza
122
Asiago
195
[Montecchio M. 42.8 kg/m2anno]
PRESTAZIONI ENERGETICHE RICHIESTE PER NUOVI EDIFICI O
RISTRUTTURAZIONI - CLASSIFICAZIONE
48) Calcolare gli indici di prestazione limite per le unità immobiliari analizzate negli
es.30 e 32 site nelle località indicate nell’es.46.
U.I
1^
1^
2^
2^
LOCALITA'
Epgl
kWh/m^2anno
Creazzo
234
Montecchio Maggiore
214
Vicenza
122
Asiago
195
ZONA
E
E
E
F
S
m^2
120.1
120.1
89.78
89.78
V
m^3
124.2
124.2
128.4
128.4
GG
2510
2351
2371
4163
[2-0.70]
49) Determinare i valori minimi e massimi per EPi in base a quelli di EPLI per la
definizione delle classi di appartenenza delle unità immobiliari analizzate nelle es.48.
unità
1
1
2
2
località
Creazzo
M.Maggiore
Vicenza
Asiago
zona
E
E
E
F
EPli
Epi
100,7
95,8
79,7
96,2
168
152
78
137
Definire poi la classe di appartenenza di ogni unità in base alla prestazione
dell’involucro EPinv (es.43)
[Vicenza: C]
50) Determinare i valori minimi e massimi per EPgl in base a quelli di EP LI per la
definizione delle classi di appartenenza delle unità immobiliari analizzate nelle s.46.
unità
1
1
2
2
località
Creazzo
M.Maggiore
Vicenza
Asiago
zona
E
E
E
F
EPli
Epgl
100,7
95,8
79,7
96,2
234
214
122
195
Definire poi la classe di appartenenza di ogni unità in base alla prestazione globale
EPgl (es.46)
[Vicenza E]
PROCEDURA DI CALCOLO SEMPLIFICATA PER LA CERTIFICAZIONE
51) Eseguire la certificazione di progetto dell’involucro edilizio del condominio di
cui è rappresentato un piano tipo nella pianta sottostante.
N
L’edificio si sviluppa su cinque piani fuori terra. Il piano terreno è adibito a garage
mentre, i quattro sovrastanti, presentano ciascuno due appartamenti di forma
simmetrica. Il sottotetto non praticabile ha la copertura a padiglione termicamente
isolata. L’altezza netta dei singoli piani è di 2,70 m, la struttura portante è realizzata in
calcestruzzo armato a pilastri (fig.1) mentre i solai sono in latero-c.to (fig.2); le
tamponature perimetrali e di separazione tra gli appartamenti e il vano scala sono
realizzate come nelle figure 1 e 2. Le finestre e le porte-finestre, a struttura lignea e
triplo vetro con tapparelle, hanno una trasmittanza complessiva U wm=1,3 W/m2K, le
porte sul vano scala hanno U=1.6 W/m2K, valori ambedue certificati dal costruttore
dei serramenti.
Figura 1 – pilastri isolati =0.26 W/m2K
Figura 2 – cordoli solaio =0.45 W/m2K
I balconi sono realizzati con il solaio a sbalzo che prosegue all’esterno delle murature
perimetrali ed è coibentato inferiormente con pannelli isolanti per esterno =0.50).
L’impianto di riscaldamento, autonomo per ogni appartamento, è a pannelli radianti a
pavimento con regolazione elettronica e caldaia a gas metano a condensazione.
L’edificio è ubicato a Chiampo in provincia di Vicenza.
[mCO2=23 kg/m2anno]
52) Eseguire la certificazione energetica di progetto dell’appartamento la cui pianta
è rappresentata nella figura sottostante.
N
L’unità immobiliare in esame si trova al terzo piano di un edificio che si sviluppa su
cinque piani fuori terra e pertanto non scambia calore con le unità immobiliari
(riscaldate) ai piani inferiore e superiore attraverso i solai. L’altezza interna è di 2,70
m. La parete nord e la quasi totalità della parete est separano l’appartamento da altre
due unità immobiliari dello stesso tipo. Solamente un breve tratto della parete est
(lungo 2,30 m) in corrispondenza dell’ingresso lo collega con il vano scala non
riscaldato. La struttura portante è a pilastri in c.a. con solai in latero-c.to. Le murature
perimetrali sono realizzate con laterizi Poroton Plan TS8 (caratteristiche indicate in
figura 3) con cappotto isolante esterno di spessore 5 cm.
Figura 3 – laterizi Poroton Plan TS8
L’isolamento dei pilastri è realizzato
come in figura 4; la disposizione
dell’isolamento elimina il ponte
termico. I ponti termici dei cordoli dei
solai sono eliminati con la stessa
tecnica d’isolamento.
Figura 4 – particolare dell’isolamento del ponte termico Y=0 e
del cappotto
I serramenti, del tipo indicato in figura 5, hanno la parte
interna realizzata in legno mentre la parte di telaio
esterno è in alluminio e vetratura tripla di serie (0.6-10.6-1-0.6)cm. Il fornitore certifica una trasmittanza
Uw=0.88 W/m2K.
Figura 5 – finestra in legno-alluminio tipo
VARION
La porta blindata ha una trasmittanza certificata dal
costruttore U=1.15 W/m2K.
L’impianto di riscaldamento è autonomo a radiatori
con regolazione on-off e caldaia a gas metano pressurizzata.
[Classi B e C]
TERMODINAMICA
53) Calcolare l’energia totale contenuta in un gas perfetto che occupa un volume di
100 dm3 alla temperatura di -5°C e alla pressione di 1,05 bar.
[U=15.7 kJ]
54) Calcolare l’energia totale di traslazione contenuta in 20 g di ammoniaca gassosa
alla temperatura di 35°C. (massa molecolare dell’ammoniaca:MM=17 g/mol)
[EcTot=4.6 kJ]
55) Una massa di 10 g di elio si trova alla temperatura di 150 °C. Calcolare l’energia
interna del gas e la velocità quadratica media.
[EcTot=13 kJ]
56) Calcolare l’energia cinetica di traslazione di una mole di un gas monoatomico
contenuto in un recipiente cubico di lato 30 cm ad una pressione di 1.75.105Pa. Calcola
poi la temperatura del gas.
[T=580K]
57) In un volume di 1000 L è contenuta una massa di gas deuterio in forma atomica a
temperatura di 425 °C e a una pressione di 12 bar. Quanto vale la massa? Quanto
misura la velocità quadratica media?
[vqm=2.9 103m/s]
58) Consideriamo una molecola biatomica di azoto. Essa può traslare lungo le direzioni
x,y,x, di un sistema di riferimento cartesiano associato al suo baricentro, con
componenti
velocità
quadratiche
medie
rispettivamente:
√< 𝑣𝑥2 >, √< 𝑣𝑦2 >, √< 𝑣𝑥2 >. Essa può inoltre ruotare attorno agli assi stessi.
a)
Con i seguenti dati: T=298K, m= 2.3.10-26kg, d=2.9.10-10m (distanza media tra gli
atomi) calcolare la velocità angolare attorno all’asse x.
b) Calcolare la forza necessaria a mantenere a questa distanza gli atomi durante la
rotazione con questa velocità. Se la forza massima di legame tra i due atomi della
molecola è di 2.0.10-10N, calcolare la velocità angolare a cui la molecola si dissocia e
la corrispondente temperatura di dissociazione.
[T=2101 k]
59) Determinare la natura di un gas sapendo che alla temperatura di 227°C la sua
velocità quadratica media vale 2497 m/s.
[H2]
60) Una massa di gas monoatomico occupa un volume di 6.0 L alla pressione di 1.00
atm. Sapendo che la velocità quadratica media delle molecole è di 600 m/s, calcolare
la massa del gas.
[m=5.1 g]
61) Determinare la natura di un gas sapendo che, alla temperatura di 27°C, una quantità
di 56 g occupa un volume di 16.42 L ed esercita una pressione di 3.04 .105Pa.
[N2]
62) Si calcoli la velocità quadratica media di un gas sapendo che la sua densità è di 3.5
kg/m3 e la pressione è di 300 kPa.
[vqm=507 m/s]
63) La massa di una molecola di gas può essere calcolata dal calore specifico c.
Considerando che l’argo ha un calore specifico c= 3.1.102J/kgK calcola la massa
atomica in g/mol e in kg.
[MM=40u]
64) Una quantità di calore Q= 20.9 J sono forniti ad un gas; ne segue che il suo volume
passa da 50.0 cm3 a 100.0 cm3 mentre la pressione rimane costante a 1.00 bar. Di
quanto cambia l’energia interna del gas? Se la quantità di gas è di 2.00 .10-3 moli
calcolare il,calore specifico molare a pressione costante e a volume costante.
[cv=26.6 J/molK]
65) Un gas monoatomico si trovano
inizialmente ad una temperatura T1=300 K e
occupano un volume V1= 1.50 L ad una
pressione di 2.00 bar. La pressione e il volume
vengono lentamente raddoppiati in modo tale
da tracciare una linea retta sul diagramma pV. Si calcolino: a) il lavoro di trasformazione;
b) la variazione di energia interna; c) il calore
fornito al sistema.
[Q=1.80 kJ]
66) In un contenitore è posta una miscela di tre gas non reattivi composta da n1= 0.50
mol di gas con calore specifico molare a volume costante cV1=12.5 J/molK, n2 = 1.0
mol di un gas con cV2 = 20.8 J/molK e n3 = 0.75 mol di un terzo gas con cV3= 29.1
J/molK. Calcolare il calore specifico molare a volume costante della miscela dei tre
gas.
[cVt=21.7 J/molK]
67) Un gas biatomico subisce una
trasformazione dallo stato A allo stato C lungo
un percorso obliquo indicato in figura. La
temperatura del gas nel punto A è TA= 1200 K,
la pressione misura pA= 5.00 kPa e il volume
VA=2.00 m2 . Durante la trasformazione la
pressione scende a pC= 2.00 kPa mentre il
volume raddoppia. Calcolare la variazione di
energia interna del gas e il calore fornito al gas.
Se anziché seguendo il percorso obliquo si arrivasse al punto C con una trasformazione
isobara seguita da una isocora quanto calore sarebbe necessario fornire al sistema?
(N.B. a questa temperatura il gas trasla, ruota e vibra)
[QABC=32 kJ]
68) Una massa di 12.0 g di ossigeno sono riscaldati a pressione di 1.00 bar da 25.0°C
a 125.0 °C. Quanto calore viene trasferito all’ossigeno? ( le molecole ruotano ma non
oscillano) Che percentuale del calore viene utilizzata per aumentare l’energia interna
dell’ossigeno?
[Q=1.09 kJ]
69) La massa di un gas occupa il volume di 4.30
L ad una pressione di 1.2 bar e una temperatura
di 310 K. Essa viene compressa diabaticamente
fino ad un volume di 0.76 L. Determinare la
pressione finale e la tempe-ratura finale. Il gas è
biatomico con molecole che ruotano ma non
vibrano.
[TA=620 K]
70) Una miscela di gas è contenuta in un volume
iniziale VA=1.00 L ed ha γ=1.30; si trova
inizialmente a TA= 273 K con una pressione di
1.00 bar. Essa viene compressa adiabaticamente
fino a metà del suo volume iniziale. Calcolare: la
sua temperatura e la pressione finali. In seguito
il gas è raffreddato fino a riportarlo a
temperatura di 273K rimanendo a pressione
costante. Quanto vale il volume finale occupato dalla miscela?
[VC=0.406 10-3m3]
71) Calcolare la costante di un processo adiabatico che comporta il passaggio di 2.0
mol di un gas biatomico attraverso uno stato avente p = 1.0 bar e T=300 K. Il gas ruota
ma non vibra.
[𝑐𝑜𝑠𝑡 = 1.5 ∙ 103 𝐽𝑚1.2 ]
72) Un gas subisce una compressione adiabatica dal seguente stato (p 1=1.00.105Pa;
V1=1.00.103m3, T1=273 K) ad uno stato con p2=1.00.1010Pa e V2=1.00 m3. Si tratta di
un gas monoatomico, biatomico o poliatomico? Quanto vale la temperatura finale?
Quante moli di gas sono presenti? Quanto vale l’energia traslazionale per mole delle
molecole prima e dopo la trasformazione?
[U2/n=350 kJ/mol]
73) Una macchina termica esegue un ciclo con
n=1.00 mol di un gas monoatomico secondo lo
schema indicato in figura. La trasformazione 12 è isocora il processo 2-3 è adiabatico mentre la
chiusura 3-1è isobara. Calcolare il calore, il
lavoro e la variazione di energia per ogni
trasformazione e per il ciclo completo sapendo
che T1= 300 K, p1=1.013.105Pa, T2= 600 K, T3= 455 K. Determinare infine il
rendimento del ciclo.
[h%=14%]
74) Un cilindro, dotato di un pistone di massa trascurabile, racchiude un gas
monoatomico in un volume V1= 10.0 dm3 quando la sua temperatura vale 0.0°C. La
massa del gas vale m=10 g e il suo calore specifico 0.20 cal/g°C. Al gas vengono forniti
100 cal di energia termica. Determina il volume finale del gas supponendo che la
pressione del gas rimanga costante durante la trasformazione.
[V2=11.8 dm3]
75) Un gas è contenuto in un recipiente. La sua temperatura è di 200°C, mentre la
pressione misura 2.00.105Pa. Determinare il valore della pressione del gas dopo che la
sua temperatura è stata portata a 400°C. Considerare la dilatazione termica del
recipiente non significativa. Sapendo che il gas è monoatomico e che il numero di moli
contenute nel recipiente è 2.00, calcola il calore fornito al sistema.
[Q=4.99 kJ]
76) 10 L di ossigeno a 5.0 atm e 30°C vengono introdotti in una bombola di capacità
20L unitamente a 25 L di azoto a 10 atm e 20°C. terminata l’operazione che avviene
con contemporaneo riscaldamento, la temperatura della miscela è di 40°C.
Determinare la massa del gas contenuto nella bombola e la pressione totale della
miscela.
[pf=1.6 106Pa]
77) Una bombola di capacità V1=20 L contiene azoto alla pressione di 10MPa e 20°C.
La bombola viene collegata con un’altra, vuota e di capacità 10 L. Dopo che il gas ha
occupato le due bombole, mantenendo la stessa temperatura iniziale, quanto vale la
pressione all’interno delle due bombole? Quanti kg di azoto sono contenuti in ciascuna
bombola?
[m2=0.77 kg]
78) Il calore specifico molare a volume costante di un gas è 25.1 J/molK. La
temperatura di 3.00 mol del gas viene innalzata di 50 K da ogn’una delle seguenti tre
trasformazioni: a volume costante, a pressione costante e attraverso una compressione
adiabatica. Calcolare per ciascuna trasformazione il calore, il lavoro e la variazione di
energia interna, trovare anche i totali di queste grandezze alla fine della
trasformazione.
[Q Tot= 8.8 kJ]
79) Un gas biatomico (ruota ma non vibra) si trova inizialmente in uno stato definito
dai seguenti parametri: n=30.0 mol, p A= 1.20 atm, VA=0.500 m3. Esso viene
trasformato in modo da percorrere un ciclo composto dalle seguenti parti:
- trasformazione isocora che porta la pressione a pB= 2.50 atm;
- espansione isobara fino ad assumere un
volume VC=2.00 m3;
- trasformazione isocora fino ad una
pressione pD=2.00 atm;
- espansione adiabatica fino a pE= pA= 1.20
atm;
- trasformazione isobara che chiude il ciclo.
Calcolare il lavoro e il rendimento del ciclo
[%=15.1%]
80) Un motore termico percorre il ciclo indicato in
figura. La miscela contenuta nel cilindro quando
si trova al punto D ha le seguenti caratteristiche:
cv=31.0 J/molK; V D=1600 cm3, TD=300 K,
pD=1.10.105Pa. La compressione adiabatica DA la
porta ad un volume VA= 100 cm3 mentre la
trasformazione isocora la fa raggiungere una
pressione pB=2pA, la successiva adiabatica BC
riporta la miscela al volume iniziale mentre
l’ultima trasformazione isocora CD ripristina lo
stato iniziale. Calcola il rendimento del ciclo.
[%=52.7%]