RC-Ramundo - ITIS MAJO

Giorgio Ramundo
4^Bi
14/12/2011
Relazione scritta di elettronica (laboratorio):
Misura 2: analisi di un circuito in regime sinusoidale
Scopo: Dato il seguente circuito, ricavare il modulo della tensione in uscita e il suo
sfasamento.
Dati:
•
•
•
•
Vpp = 10 V
f = 2 kHz
C = 8,2 nF
R = 18 kΩ
Risoluzione del problema
Risoluzione sperimentale
La sperimentazione avviene con l’oscilloscopio, strumento di misura elettronico
che consente di visualizzare l'andamento temporale dei segnali elettrici. Lo
schema per collegare ciò che ci serve è il seguente:
Giorgio Ramundo
4^Bi
14/12/2011
Fatto questo, a video appariranno i due segnali periodici, e da questa
visualizzazione sarà possibile calcolare due variabili fondamentali: ΔT e T, che ci
serviranno a calcolare lo sfasamento, con l’ausilio della seguente formula:
Il modulo si calcola contando i quadretti da picco a picco della forma d’onda
rappresentante la tensione in uscita creata dall’oscilloscopio.
Occorre, per ricavare un risultato plausibile, tenere conto della scala che i
quadretti rappresentano.
Risoluzione simulata
Per calcolare lo sfasamento occorre utilizzare la formula già vista nella risoluzione
sperimentale:
E’ la stessa formula di prima, dato che la frequenza è il reciproco del periodo.
Per ricavare
e il modulo occorre creare il grafico con Micro-Cap.
Giorgio Ramundo
4^Bi
14/12/2011
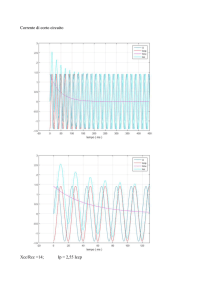
La forma d’onda rossa rappresenta la tensione d’uscita, quella blu quella
d’entrata.
Per ottenere ciò, ho creato il circuito con l’ausilio dei componenti virtuali, poi ho
avviato l’analisi Transient.
Successivamente sono entrato in Scale Mode e ho selezionato un’area dell’onda.
Fatto questo, sono entrato in Cursor Mode e ho cliccato sulle due forme d’onda,
una volta con il tasto sinistro e una volta con il tasto destro.
In basso sono apparsi dei dati: basterà appuntarsi il terzo dato della colonna Delta
per dire di aver trovato
.
Dopodichè occorre calcolare con la formula lo sfasamento.
I risultati, alla fine dell’analisi sperimentale e pratica, sono i seguenti:
Pratica
Simulazione
|Vo| [Vpp]
3,80
4,206
ΔVo [°]
67
66
Giorgio Ramundo
4^Bi
14/12/2011
Risoluzione teorica
Calcolo del modulo e dello sfasamento
1
1
1



j
* 10 9   j3,88 * 10 5 * 10 9   j3,88 * 10 4 
9
jC j * 2 * f * 8,2 * 10
6,28 * 500 * 8,2
 j38,84 k
Zc 
Rtot  Zc  R  j 38,84  18 k
Vmax 
V pp
2
 5,00 V
5
90  j194,20

 0,05  j 0,11 mA
18  j38,84
1832,55
Vo R * I tot  18(0,05  j 0,11)  0,9  j1,98 V
I tot 
| Vo | 0,9 2  1,98 2  0,81  3,92  4,73  2,17 * 2  4,35
Vo  arctg (
1,98
)  65,5
0,9
Conclusioni
I valori risultati dalla risoluzione sperimentale e pratica sono quasi esatti.
Maggior scostamento nella pratica, forse dovuto all’imprecisione della misura
dell’oscilloscopio.
Il lavoro è andato per le lunghe, ma posso dire che è stato davvero utile per
ampliare le conoscenze che solo in teoria avevo l’opportunità di acquisire.
Esercizio impegnativo, ma molto coinvolgente.
Giorgio Ramundo
4^Bi
14/12/2011
Analisi
Guardando il circuito, ci si accorge subito della presenza di due elementi che
abbiamo iniziato ad analizzare all’inizio di questo quarto anno scolastico:
 Un generatore di tensione alternata (tensione variante nel tempo);
 Un condensatore;
Analizziamo ciò che ci chiede il problema: ricavare il modulo della tensione in
uscita e il suo sfasamento.
La tensione in uscita la dobbiamo calcolare con la legge di Ohm:
equivale al rapporto tra resistenza totale e tensione massima del generatore,
che possiamo ricavare dividendo per due la tensione che il testo ci fornisce.
L’esistenza di un condensatore rende impossibile, però, trovare immediatamente
la resistenza totale.
Per risolvere questo problema, dobbiamo ricavare l’impedenza di quest’ultimo,
esprimibile in ohm, così da poterlo sommare con la resistenza e ricavare il valore
che ci serve.
La formula per ricavare l’impedenza è la seguente:
Dove rappresenta il prodotto tra 2π e la frequenza del generatore.
Trovato questo, ricaveremo la
usando come resistenza totale la somma tra
.
Il risultato sarà un numero complesso, non appartenente all’insieme dei numeri
reali (la j che si trova nella formula altro non è che la radice quadrata di -1), di
questo genere:
Dove R e I rappresentano rispettivamente la parte reale e la parte immaginaria.
Il modulo e lo sfasamento della tensione in uscita si calcolano, rispettivamente,
nel seguente modo:
Giorgio Ramundo
4^Bi
14/12/2011
(teorema di Pitagora)
(arcotangente, funzione goniometrica, del rapporto tra la parte immaginaria e la parte reale)
Il generatore di tensione alternata presenta due nuovi parametri, che non
abbiamo mai visto in elettronica prima di quest’anno:
 La tensione picco a picco (voltaggio totale entro il punto (picco) più alto e il
punto (picco) più basso di una tensione di corrente alternata;
 La frequenza (grandezza che concerne fenomeni periodici o processi
ripetitivi, Il suo reciproco è il periodo, cioè il tempo entro il quale una forma
d’onda compie un’oscillazione e torna alla condizione iniziale);