capitolo
2
L’insieme dei numeri naturali e l’insieme degli interi Criteri di divisibilità
La proprietà 3 della divisibilità permette di riconoscere che il numero
a = x ⋅ b + c è divisibile per b se e solo lo è l’addendo c:
a=x⋅b+c
b a ⇔ bc
Questo fenomeno permette di riconoscere alcuni semplici criteri di divisibilità che illustriamo riferendoci, per semplicità, a numeri di sole 3 cifre: l’estensione del caso generale è quasi sempre evidente.
Sia dunque x = abc, dove a indica le centinaia, b le decine, c le unità; si ha:
x = a ⋅ 100 + b ⋅ 10 + c
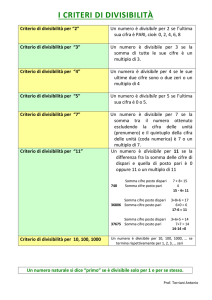
Si riconosce facilmente che un numero è divisibile:
per 2 se termina con una cifra pari: 0, 2, 4, 6, 8
Tenuto conto che 100 = 2 ⋅ 50, 10 = 2 ⋅ 5 si ha:
x = (a ⋅ 50 + b ⋅ 5) ⋅ 2 + c
2x ⇔ 2c
Per esempio, 236 è divisibile per 2, 235 no.
per 3 se la somma delle sue cifre è divisibile per 3
Tenuto conto che 100 = 3 ⋅ 33 + 1, 10 = 3 ⋅ 3 + 1 si ha:
x = (a ⋅ 33 + b ⋅ 3) ⋅ 3 + a + b + c
3x ⇔ 3 (a + b + c)
Per esempio, 537 = 5 ⋅ 100 + 3 ⋅ 10 + 7 = 5 ⋅ (3 ⋅ 33 + 1) + 3 ⋅ ( 3 ⋅ 3 + 1) + 7 =
= 3 ⋅ (5 ⋅ 33 + 3 ⋅ 3) + 5 + 3 + 7
e poiché
5 + 3 + 7 = 15 è divisibile per 3, anche 537 è divisibile per 3.
per 9 se la somma delle sue cifre è divisibile per 9
Tenuto conto che 100 = 9 ⋅ 11 + 1, 10 = 9 + 1 si ha:
x = (a ⋅ 11 + b) ⋅ 9 + a + b + c
9x ⇔ 9 (a + b + c)
Per esempio, 828 = 8 ⋅ 100 + 2 ⋅ 10 + 8 = 8 ⋅ (11 ⋅ 9 + 1) + 2 ⋅ ( 9 + 1) + 8 =
= 9 ⋅ (8 ⋅ 11 + 2) + 8 + 2 + 8
e poiché
8 + 2 + 8 = 18 è divisibile per 9, anche 828 è divisibile per 9.
per 5 se termina per 0 o per 5
Tenuto conto che 100 = 20 ⋅ 5, 10 = 2 ⋅ 5 si ha:
x = (a ⋅ 20 + b ⋅ 2) 5 + c
5x ⇔ 5 c
Per esempio, 755 è divisibile per 5, 557 no.
per 25 se termina con 00, 25, 50 o 75
Tenuto conto che 100 = 4 ⋅ 25 si ha:
x = a ⋅ 4 ⋅ 25 + 10 ⋅ b + c
25x ⇔ 25(10b + c)
relazione che equivale a dire che il numero di due cifre bc deve essere multiplo di 25:
bc = 00, bc = 25, bc = 50, bc = 75.
Per esempio, 250 è divisibile per 25.
1
© 2010 RCS Libri S.p.A., ETAS - L. Lamberti, L. Mereu, A. Nanni - Corso di Matematica - Edizione mista
capitolo
2
L’insieme dei numeri naturali e l’insieme degli interi per 4 se le sue ultime due cifre a destra formano un numero divisibile per 4 oppure sono due zeri
Tenuto conto che 100 = 4 ⋅ 25 si ha:
x = a ⋅ 25 ⋅ 4 + 10b + c
4 x ⇔ 4 (10b + c)
relazione che equivale a dire che il numero di due cifre bc deve essere divisibile per 4.
Per esempio, 716 è divisibile per 4, 16 è divisibile per 4.
per 11 quando lo è la differenza tra la somma delle cifre di posto dispari e la somma
di quelle di posto pari
Tenuto conto che 100 = 9 ⋅ 11 + 1, 10 = 11 – 1 si ha:
x = (a ⋅ 9 + b) ⋅ 11 + a – b + c
11x ⇔ 11(a – b + c)
a + c è la somma delle cifre di posto dispari e b è la somma delle cifre di posto pari.
Per esempio, tenuto conto che 1000 = 9 ⋅ 112 – 8 ⋅ 11 – 1, risulta:
9779 = 9 ⋅ 1000 + 7 ⋅ 100 + 7 ⋅ 10 + 9 =
= 9 ⋅ (9 ⋅ 112 – 8 ⋅ 11 – 1) + 7 ⋅ ( 9 ⋅ 11 + 1) + 7 ⋅ (11 – 1) + 9 =
= 11 ⋅ ( 81 ⋅ 11 – 72 + 63 + 7) – 9 + 7 – 7 + 9
e poiché – 9 + 7 – 7 + 9 = 0 è divisibile per 11, anche 9779 è divisibile per 11.
per 10 se termina con uno 0, per 100 se termina con due zeri, ecc.
Infatti:
x = (10 ⋅ a + b) ⋅ 10 + c
10 x ⇔ 10 c
Osservazione
a. I due criteri di divisibilità di un numero n per 3 o per 9 sono espressi dall’analoga proprietà del numero somma delle cifre che compongono n; quindi tutti i numeri ottenibili permutando l’ordine di tali cifre restano divisibili per 3 o per 9 se
tale era n.
Per esempio:
• n = 384 è divisibile per 3, allora lo sono, ovviamente anche i numeri 348, 834,
843, 438, 483.
• 3555 è divisibile per 9, allora lo sono anche i numeri 5355, 5535, 5553.
b. Sulla scia dei criteri precedenti se ne possono produrre altri: occorre fare attenzione, tuttavia, che il criterio prodotto non diventi inutilmente complesso e quindi poco utile.
Consideriamo per esempio il criterio di divisibilità per 6:
tenuto conto che 100 = 16 ⋅ 6 + 4, 10 = 1 ⋅ 6 + 4 si ha, sempre per il numero di 3
cifre x = abc,
x = (a ⋅ 16 + b ⋅ 2) ⋅ 6 + 4 ⋅ a + 4 ⋅ b + c
6 x ⇔ 6(4a + 4b + c)
Così riconosciamo che 726 è divisibile per 6 essendo 4 ⋅ 7 + 4 ⋅ 2 + 6 = 42 = 7 ⋅ 6.
Forse eseguire il test ha richiesto tanto tempo quanto riconoscere la divisibilità direttamente!
2
© 2010 RCS Libri S.p.A., ETAS - L. Lamberti, L. Mereu, A. Nanni - Corso di Matematica - Edizione mista