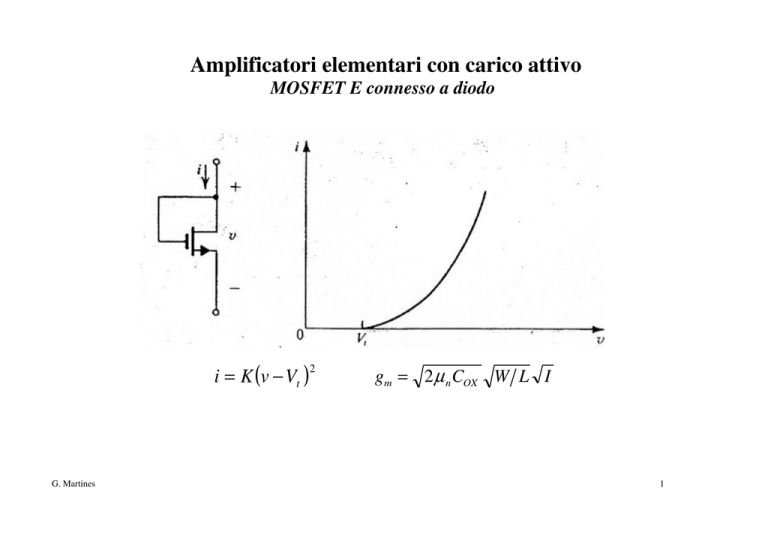
Amplificatori elementari con carico attivo
MOSFET E connesso a diodo
2
i = K (v − Vt )
G. Martines
gm = 2 µ n COX W L I
1
MOSFET DE connesso a diodo
vGS = 0 , il transistore può funzionare in regione di triodo o di pinch off ma su una sola curva
i = K ( −2VtD v − v 2 ) in regione di triodo
2
tD
i = KV = I DSS
G. Martines
in regione di pinch off
ed in questo caso
v
i = KVtD2 1 +
VA
2
Generatore di Corrente Elettronico
La corrente attraverso il generatore ideale è indipendente
dalla tensione ai suoi capi e la resistenza di uscita è infinita
Nei generatori di corrente elettronici, la corrente dipende
dalla tensione ai terminali ed essi hanno una resistenza di
uscita finita.
I generatori di corrente a singolo
transistore funzionano solo in un
quadrante del piano i-v e hanno una
elevata resistenza di uscita.
La figura di
merito VCS è
definita da
V EE
R=V EE
R
1/λ+V DS 1
= +V DS
per un transistore V CS = I D r o= I D
λ
ID
V CS = I O Rout ; per un resistore vale V CS =
G. Martines
3
Generatore di Corrente di Widlar (Elevata Resistenza di Uscita)
Le equazioni di progetto sono quelle viste per la polarizzazione a quattro resistenze:
R4
2I O
V G =
V SS e V GS =V TN +
quindi
( R3 + R4 )
KN
V +V SS V GS V G+V SS
RS = G
≈
IO
IO
√
Per la resistenza di uscita, dal modello equivalente a
piccolo segnale del transistore si ottiene:
Rout =R S +r o (1+g m R S )=r o +(1+g m r o ) RS ≈µ f RS
V ss
Allora V CS ≈µ f
se si applica il criterio del 1/3,
3
cioè I O R S ≈V SS / 3
G. Martines
4
Generatore di corrente costante a specchio di corrente
Principio di funzionamento
Le correnti di uscita sono uguali se i transistori sono uguali, ma possono avere valori
significativamente diversi se, ad esempio, è diverso il rapporto W/L in M1 ed M2.
G. Martines
5
Generatore di corrente costante a specchio di corrente
Le equazioni di progetto
per effetto della iniezione di corrente in M
2I REF
ma V GS1=V GS2 e
V GS1 =V TN1+
K N1 (1+λ V DS1 )
K
quindi I O = N (V GS1V TN2)2 (1+λ V DS2 ) il rapporto
2
di riflessione (mirror ratio) per transistori uguali è
I
(1+λ V DS2 )
MR= O =
I REF (1+λ V DS1 )
√
poiché per un FET
connesso a diodo vale la
v 1 ed il generatore
≈
i gm
di IREF è ideale.
G. Martines
6
Circuiti per la distribuzione della corrente di polarizzazione
Tutti i transistori hanno i gate connessi ad un unico nodo ed i drain possono essere
connessi a tensioni di alimentazione diverse. Le correnti di drain dipenderanno dai
I Oi (W / L)i (1+λ V DSi )
=
rapporti di riflessione di ciascuno specchio e da MRi =
.
I ref (W / L)1 (1+λ V DS1 )
G. Martines
7
Lo specchio di corrente di Widlar
Per determinare il rapporto di riflessione
2I REF
2I O
V GS1V GS2
K N1
K N2
I O=
=
R
R
Da cui
I O (W / L)1 ed
1 2I REF
I O=
1
R K N1
I REF (W / L)2
infine
√ √
√ ( √
IO
I REF
=
1
R
√
( √
I O (W / L)1
2
1
I REF K N1
I REF (W / L)2
)
)
Per la resistenza di uscita Rout, dal modello equivalente a piccolo segnale del transistore
connesso a diodo, si ottiene:
Rout =R+r o2 (1+ g m2 R)=r o2 +(1+ g m2 r o2 ) R≈µ f2 R
G. Martines
8
Specchio di corrente di Wilson
Principio di funzionamento
Tutti i transistori sono in saturazione e
I D3 =I D1= I O ed I D2=I REF .
Se i transistori sono tutti uguali, allora anche
V GS3=V GS1 e deve essere
I D2 (1+2 λ V GS )
=
I D1 (1+λ V GS )
Quindi
(1+λ V GS )
I O = I REF
(1+2 λ V GS )
√
con V ≈V + 2I REF
GS
TN
KN
Il vantaggio non è nel rapporto di riflessione ma nel valore della resistenza di uscita.
G. Martines
9
Specchio di corrente di Wilson
La resistenza di uscita.
v x =v 3+v 1=(i x g m3 v gs )r o3+
ix
ix
v
=v
v
=g
r
v
v
=(1+µ
)
con gs 2 1
m2 o2 1
1
f2
g m1
g m1
quindi:
Rout =r o3 [1+
g m3
1
(1+µ f2)]+
g m1
g m1
Se i transistori sono uguali, allora
g m1=g m2 = g m3 e si può scrivere
1
Rout ≈r o3 (2+µ f + µ )≈µ f r o3
f
µf
Infine V CS ≈ λ
3
G. Martines
10
Il generatore di corrente cascode
per le correnti si ha I D3 =I D1= I REF e
I O = I D4= I D2 mentre
V DS2=V GS1+V GS3V GS4
Inoltre, se tutti i transistori sono uguali, allora
V DS2=V GS =V DS1 e ne consegue che deve
essere esattamente I O = I REF
nello specchio costituito da M1 ed M2.
Il circuito equivalente per la determinazione della resistenza di uscita presenta 1/gm al posto dei MOS connessi a diodo. Il generatore controllato è nullo, quindi
R out =r o4 (1+ g m4 r o2 )≈µ f4 r o2
G. Martines
11
Stadio CS con carico MFOSFET E connesso a diodo
2
i D = K1 (v I − Vt )
G. Martines
2
e iD = K 2 (vGS 2 − Vt )
ovvero
i D = K 2 (V DD − vO − Vt )
2
12
Transcaratteristica del CS con
carico connesso a diodo
K 1
K1
vO = V DD − 1 −
V
−
vI
t
K 2
K2
G. Martines
13
Modello equivalente a piccolo segnale
Av = − g m1 (1 g m 2 // ro1 // ro 2 ) ≈ − g m1 g m 2
v
K1
=
Av ≡ O = −
vI
K2
G. Martines
(W L )1
(W L )2
14
BODY EFFECT nei FET
Nota : generalmente si ha 0 < η < 1
G. Martines
15
Effetto Body e degrado della prestazione
Il bulk di Q2 non può essere connesso al source ma alla massa e
quindi nasce l’effetto body:
Av = − g m1 (1 g m 2 // 1 g mb 2 // ro1 // ro 2 ) ≈ − g m1 (g m 2 + g mb 2 )
potendo porre gmb = χgm con χ tipicamente compreso fra 0.1 e
0.3, si ottiene:
− gm1 1
Av ≈
g m2 1 + χ
cioè una significativa riduzione del guadagno di tensione.
G. Martines
16
Stadio CS con MOSFET E e carico MOSFET DE
connesso a diodo
Con vGS 2 = 0 il modello equivalente a piccolo segnale di Q2 si riduce
alla sola ro2 e quindi nella regione III:
Av = − g m1 (ro1 // ro 2 )
G. Martines
17
Stadio CS con MOSFET E e carico MOSFET DE connesso a diodo
Modello equivalente a piccolo segnale in presenza di effetto body
g
Av = − g m1 1
// ro1 // ro 2 ≈ − m1
g mb 2
g mb 2
gm1 1
Av ≈ −
g m2 χ
Nota: la corrente di polarizzazione è necessariamente la IDSS del MOSFET DE e può essere
variata solo cambiando il layout del transistore DE.
G. Martines
18
Generatore di corrente costante a specchio di corrente con MOSFET
2
2
Poiché I REF = K1 (VGS − Vt ) ed I O = K 2 (VGS − Vt ) in regione di saturazione, allora:
I O = I REF
G. Martines
(W L )2
K2
= I REF
K1
(W L )1
ed
RO = ro 2 =
VA
I REF
19
Amplificatore CMOS (carico attivo a specchio di corrente)
G. Martines
20
Trans-caratteristica dell’amplificatore CMOS
Av =
vo
= − g m1 (ro1 // ro 2 )
vi
g m1 = 2 K n I REF e ro1 = ro 2 =
Av = −
G. Martines
VA
I REF
VA K n
I REF
21