ISTITUTO PROVINCIALE DI CULTURA E LINGUE “NINNI CASSARÀ”
LA FORZA NEL MOTO CURVILINEO
CLASSI III A E III B
Prof. Erasmo Modica
[email protected]
www.galois.it
IL MOTO CIRCOLARE UNIFORME – RICHIAMI
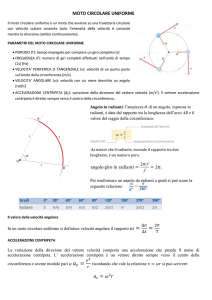
Un corpo si muove di moto circolare uniforme se il modulo della sua velocità non
varia nel tempo.
Il fatto che non vari il modulo, non vuol dire che il vettore velocità sia costante. Infatti,
com’è possibile notare in figura, varia la direzione del vettore velocità che risulta essere
sempre tangente alla traiettoria circolare descritta dal corpo in movimento.
Si definisce periodo T del moto circolare l’intervallo di tempo impiegato da un corpo per
compiere un giro completo; mentre si definisce frequenza f, l’inverso del periodo, cioè:
Se la circonferenza ha raggio R, l’espressione del modulo della velocità tangenziale è
data dalla relazione:
L’accelerazione del corpo, detta accelerazione centripeta, è invece diretta verso il
centro della circonferenza e la sua espressione è data dalla relazione:
LA FORZA CENTRIPETA
Facendo ruotare una pallina legata a un filo, essa si muoverà di moto circolare uniforme.
Poiché varia la direzione della velocità, la pallina subisce un’accelerazione dovuta alla forza
applicata dalla mano. La direzione di tale forza è perpendicolare alla traiettoria ed è
rivolta verso il centro di rotazione. Proprio per tale ragione, questa forza viene chiamata
forza centripeta e indicata col simbolo .
ISTITUTO PROVINCIALE DI CULTURA E LINGUE “NINNI CASSARÀ”
Definizione. Dicesi forza centripeta quella forza che agisce
su un corpo con intensità costante e in direzione sempre
perpendicolare al movimento, originando un moto circolare
uniforme.
Per la seconda legge della dinamica, l’espressione di tale forza
sarà:
LA FORZA CENTRIFUGA
Se si considera una pattinatrice su ghiaccio che viene fatta ruotare dal suo compagno, essa
risente di una forza che la spinge verso l’esterno. Poiché la pattinatrice sta ruotando,
risente della forza centripeta che viene esercitata su di essa dalla mano del compagno.
Inoltre sembra risentire anche di una forza che ha la stessa direzione e intensità di quella
centripeta, ma verso opposto.
Un osservatore esterno non nota tale forza, ma riconosce la sola presenza della forza
centripeta. Un osservatore che ruota insieme alla pattinatrice, vede il corpo della ragazza
fermo e quindi, poiché su di essa agisce la forza centripeta , deve esistere una forza
uguale e contraria a essa tale che la loro somma sia nulla. Questa forza prende il nome di
forza centrifuga.
Definizione. Dicesi forza centrifuga una forza apparente che ha la stessa direzione e
intensità della forza centripeta, ma verso opposto.
La forza centrifuga è una diretta conseguenza dell’inerzia dei corpi che si muovono di moto
curvilineo. Essi tendono a muoversi di moto rettilineo uniforme e ciò è provato dal fatto
che se il pattinatore lasciasse la sua compagna, essa “sfuggirebbe” in direzione tangente al
moto rotatorio e non verrebbe più spinta verso l’esterno. Quindi la forza centrifuga esiste
solo perché esiste la forza centripeta.
MOTO IN CURVA
Quando si effettua una curva in motorino, possiamo considerarla un tratto di circonferenza
di raggio R, detto raggio di curvatura. Se la moto ha una massa pari a m, la forza
centripeta che gli permette di effettuare la curva ha espressione
.
Tale forza è esercitata dall’asfalto sul motorino ed è uguale alla forza di attrito
esercita tra l’asfalto e gli pneumatici. Quindi si ha che:
che si
Se la velocità della moto aumenta, aumenta anche la forza d’attrito, ma essa non aumenta
all’infinito, bensì fino al raggiungimento del valore massimo dato dall’espressione:
E. Modica, 2011/2012
www.galois.it
2
ISTITUTO PROVINCIALE DI CULTURA E LINGUE “NINNI CASSARÀ”
Quindi possiamo ottenere la velocità massima
con cui una curva può essere affrontata
senza sbandare, ricavando la v dalla seguente relazione:
Da cui:
ovvero:
√
PROBLEMI
Problema 1. Un corpo di massa 2 kg si muove di moto circolare uniforme con velocità
⁄ . Determinare il modulo della forza centripeta, sapendo che il raggio è pari a 8
m.
Sostituendo i valori nell’espressione della forza centripeta, si ottiene:
Problema 2. Un corpo di massa 8 kg si muove di moto circolare uniforme con velocità
⁄ . Determinare il raggio della circonferenza, sapendo che esso risente di una
forza centripeta pari a 10 N.
Dall’espressione della forza centripeta si ricava:
Problema 3. Determinare la massa di un corpo che si muove di moto circolare
uniforme, sapendo che esso risente di una forza centripeta pari a 9 N, che il raggio della
⁄ .
circonferenza è uguale a 4 m e che la sua velocità
Dall’espressione della forza centripeta si ricava:
E. Modica, 2011/2012
www.galois.it
3
ISTITUTO PROVINCIALE DI CULTURA E LINGUE “NINNI CASSARÀ”
Problema 4. Determinare la velocità di un corpo che si muove di moto circolare
uniforme, sapendo che esso risente di una forza centripeta pari a 5 N, che il raggio della
circonferenza è uguale a 4 m e che la sua massa è
.
Dall’espressione della forza centripeta si ricava:
√
√
Problema 5. Determinare la velocità massima con cui un’automobile di 800 kg può
affrontare una curva senza sbandare, sapendo che la curva ha un raggio di 6 m e che il
coefficiente di attrito tra l’asfalto e gli pneumatici è pari a 0,5.
Come visto nel paragrafo precedente, si ha:
√
E. Modica, 2011/2012
www.galois.it
√
√
4