Teoria Cinetica ed Equazione
di Stato dei Gas Perfetti
07/05/15
Temperatura e Calore
1
Introduzione al Problema
Obiettivo della Teoria Cinetica dei
Gas (TCG) è spiegare le proprietà
macroscopiche (pressione, volume
e temperatura di un gas) partendo
dalla conoscenza delle variabili
microscopiche, ad esempio la
velocità delle molecole che
compongono il gas.
Caso di studio: trovare la relazione
tre la pressione esercitata dal gas
sulle pareti e la velocità delle
molecole.
07/05/15
Temperatura e Calore
2
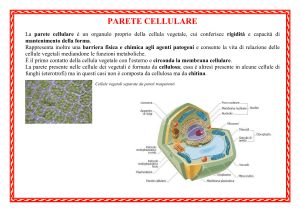
Definizione di Gas Perfetto
Il gas perfetto è:
1) Formato da N corpuscoli
puntiformi di massa m*
2) Il Volume dei corpuscoli è
molto minore del volume
occupato dal gas
3) I corpuscoli NON sono soggetti
a forza di gravità
4) Non ci sono urti tra i corpuscoli
ma solo tra i corpuscoli e le
pareti del contenitore
5) Gli urti sono elastici
07/05/15
Temperatura e Calore
3
Urto sulla parete di una molecola di gas
o Consideriamo un punto materiale
(molecola di gas) che urta
“elasticamente” sulla parete de
contenitore.
o Chiamiamo q il modulo della sua
quantità di moto: q = mv
(Non usiamo p per non conforderci con la pressione)
07/05/15
Temperatura e Calore
4
Urto sulla parete di una molecola di gas
07/05/15
Temperatura e Calore
5
Urto sulla parete di una molecola di gas
07/05/15
Temperatura e Calore
6
Urto sulla parete del corpuscolo i-esimo
Se q è la quantità di moto del corpuscolo, a causa dell’urto:
*
*
Δq corpuscolo = −2m v i ⇒ Δq parete = 2m v i
Caratteristiche dell’urto:
Il corpuscolo urta di nuovo la parete dopo
aver percorso uno spazio s = 2l
Tempo necessario (periodo) = 2l/vi
Numero di collisioni per unità di tempo (frequenza) = vi / 2l
07/05/15
Temperatura e Calore
7
Urto sulla parete del corpuscolo i-esimo
La quantità di moto trasmessa alla parete nell’unità di tempo è:
Δq parete Δq totale
=
= 2m* v i ⋅ v i /2l = m* v 2 i /l
Δt
Δt
Per semplicità consideriamo che solo N/3 corpuscoli colpiscano la
Parete, perperdicolarmente ad essa (ma il risultato è comunque corretto).
La quantità di moto trasmessa alla parete nell’unità di tempo da N/3
€
Corpuscoli
è la FORZA (2° Principio della Dinamica)
N /3
2
v
∑ i
N /3
* N /3
*
m
N
m
2
i=1
F = ∑ m* v 2 i /l =
v
⋅
i =
∑
l i=1
3 l N/3
i=1
07/05/15
Temperatura e Calore
8
Distribuzione delle velocità nel gas
07/05/15
Temperatura e Calore
9
Urto sulla parete del corpuscolo i-esimo
N /3
∑v
2
i=1
N/3
i
= v2i
La grandezza <vi2> è il valor medio della velocità al quadrato, e prende il
nome di velocità quadratica media.
N m* 2
F N m* 2
N m* 2
€v i ⇒ p = 2 = ⋅ 3 v i = ⋅
F= ⋅
vi
3 l
l
3 l
3 V
Possiamo finalmente calcolare il prodotto della pressione per il volume!
2N 1 * 2
2N
pV =
mvi =
EK
3 2
3
07/05/15
Temperatura e Calore
10
Equazione di stato dei gas perfetti
2N
pV =
EK
3
A misura della energia cinetica molecolare media (grandezza microscopica)
assumiamo il parametro macroscopico TEMPERATURA. Ovvero la
temperatura è una misura della energia cinetica molecolare media <EK2>.
T ∝ EK
2N
€
⇒ E K = CT ⇒ pV =
CT ⇒ pV = nN AkT = nRT
3
pV = nRT
Equazione di stato dei gas perfetti
€
07/05/15
Temperatura e Calore
11
Le costanti (molto) importanti
n è il numero di moli
N A = Numero di Avogadro = 6.02 ⋅10 23 mol−1
k = costante di Boltzmann = 1.38 ⋅10 -23 J/K
R = Costante dei Gas = 8.314 J/mol⋅ K
€
07/05/15
Temperatura e Calore
12