APPUNTI DI ELETTROMAGNETISMO

Matematica e Fisica
Schema elettromagnetismo
APPUNTI DI ELETTROMAGNETISMO
Sintesi
1 PRODURRE CORRENTI CON CAMPI MAGNETICI
Se le correnti producono campi magnetici, un campo magnetico può produrre una corrente?
Risposta di Faraday ed Henry:
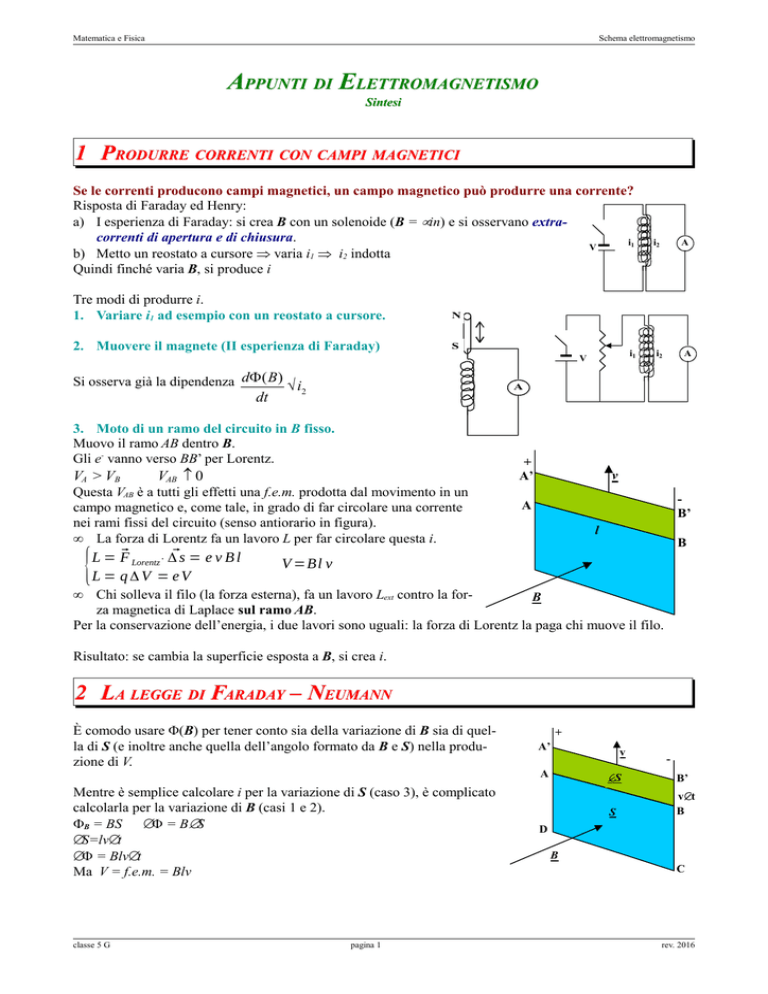
a) I esperienza di Faraday: si crea B con un solenoide (B = µin) e si osservano extracorrenti di apertura e di chiusura.
i1
V
b) Metto un reostato a cursore ⇒ varia i1 ⇒ i2 indotta
Quindi finché varia B, si produce i
Tre modi di produrre i.
1. Variare i1 ad esempio con un reostato a cursore.
N
2. Muovere il magnete (II esperienza di Faraday)
S
i1
V
Si osserva già la dipendenza dΦ ( B ) ÷ i
dt
+
A’
VAB ≠ 0
Questa VAB è a tutti gli effetti una f.e.m. prodotta dal movimento in un
campo magnetico e, come tale, in grado di far circolare una corrente
nei rami fissi del circuito (senso antiorario in figura).
• La forza di Lorentz fa un lavoro L per far circolare questa i.
{
⃗ Lorentz ⋅ ∆⃗s = e v B l
L= F
L = q∆V = eV
•
A
i2
A
A
2
3. Moto di un ramo del circuito in B fisso.
Muovo il ramo AB dentro B.
Gli e- vanno verso BB’ per Lorentz.
VA > VB
i2
v
B’
A
l
B
V =Bl v
Chi solleva il filo (la forza esterna), fa un lavoro Lext contro la forB
za magnetica di Laplace sul ramo AB.
Per la conservazione dell’energia, i due lavori sono uguali: la forza di Lorentz la paga chi muove il filo.
Risultato: se cambia la superficie esposta a B, si crea i.
2 LA LEGGE DI FARADAY – NEUMANN
È comodo usare Φ(B) per tener conto sia della variazione di B sia di quella di S (e inoltre anche quella dell’angolo formato da B e S) nella produzione di V.
+
A’
A
Mentre è semplice calcolare i per la variazione di S (caso 3), è complicato
calcolarla per la variazione di B (casi 1 e 2).
ΦB = BS
∆Φ = B∆S
∆S=lv∆t
∆Φ = Blv∆t
Ma V = f.e.m. = Blv
classe 5 G
pagina 1
v
-
∆S
B’
S
v∆t
B
D
B
C
rev. 2016
Matematica e Fisica
f .e.m. = −
In generale:
Schema elettromagnetismo
dΦ B
dt
(per un solenoide f .e.m. = − N
dΦ B
)
dt
dΦ B dB
dS
d (cosθ )
S cos θ + B cos θ + BS
=
dt
dt
dt
dt
Il segno meno richiede una spiegazione particolare.
• Si considerano positivi il verso di S concorde con B e, conseguentemente, il verso (destrorso) di percorrenza del circuito, sia per i che per V (decrescente).
• In tal modo Φ è sempre positivo e ∆Φ è positivo se Φ cresce.
• Dunque, quando ∆Φ è positivo V è negativo e viceversa.
Questo segno meno nella legge di Faraday Neumann ha un significato fisico fondamentale espresso dalla
legge di Lenz:
La corrente indotta è tale da produrre Bindotto = -∆B .
Questo è derivabile dal principio di conservazione dell’energia. Se fosse il contrario si avrebbe contemporaneamente la i2 indotta e un lavoro sul magnete.
Conservazione
dell’energia
XIX secolo
Legge di Lenz
N
S
Bi
S
XX secolo
N
S
N
La legge trovata si applica a numerose situazioni fisiche reali, ma è una forma particolare di una legge più
generale che si trova spostando l’attenzione sul campo elettrico indotto E (di un nuovo tipo, affatto diverso
da quello elettrostatico) che è associato alla f.e.m.
Finché il ramo AB si muove nel campo B come in figura, questo nuovo campo E è presente solo in AB ed è
rivolto da BB’ verso AA’.
Se calcoliamo la circuitazione di questo E lungo il percorso chiuso A’B’CD (verso positivo di B e di S) troviamo quindi:
ΓE = −
dΦ B
dt
legge di Faraday-Neumann
Il campo elettrico indotto ha ΓE non nullo.
Un campo elettrico indotto non è conservativo come quello elettrostatico.
La portata della legge sta nel fatto che non è la presenza della spira conduttrice a
produrre E. Il conduttore serve solo a visualizzarne gli effetti:
N
Ove si abbia un campo magnetico variabile nel tempo si ha
un campo elettrico indotto non conservativo (anche nel vuoto).
∆B
E
La non conservatività del campo è connessa con la chiusura delle sue linee di forza.
S
classe 5 G
pagina 2
rev. 2016
Matematica e Fisica
Schema elettromagnetismo
La circuitazione di E va calcolata seguendo il verso positivo
del campo B concatenato.
In figura (a):
Γs ( E ) > 0,
In figura (b):
Γs ( E ) < 0,
dφ ( B )
<0.
dt
dφ ( B )
> 0.
dt
i+di
i-di
E
B-dB
s
s
B+dB
(a)
E
(b)
Figura 31-13 (Halliday liceo).
Dati:
L = 4 cm, b = 10 cm, d = 15 cm,
R = 1.6 Ω, B = 2 T, v = 1 m/s.
Figura 31-14 (Halliday liceo).
(a) Campo B uniforme nel disco in colore e uni-
formemente crescente nel tempo.
(b) Calcolo della circuitazione per una circonferenza di raggio r (E uniforme su crf per simmetria):
Γ( E)=2 π r E=− π r 2
dB
dt
E=−
1 dB
r
2 dt
(c) Questo spiega la densità maggiore di linee di
E a distanza maggiore. Ma anche perché si abbia un campo residuo fuori da B.
All’esterno infatti E deve andare come 1/r affinché sia nulla la circuitazione 4 in figura d (prendere all’esterno di B una linea chiusa con due
archi concentrici e due segmenti radiali)
(d) Linee chiuse uguali racchiudono aree uguali
e dunque hanno uguali
dΦ B
e uguali f.e.m. nei
dt
casi 1 e 2, f.e.m. minore nel caso 3 e f.e.m. nulla nel caso 4.
classe 5 G
pagina 3
rev. 2016
Matematica e Fisica
Schema elettromagnetismo
3 APPLICAZIONI
3.1 ALTERNATORE
Φ = BS cos(ωt + ϕ 0 )
f em = −
dΦ
= BSω sen(ωt + ϕ 0 )
dt
S
B
ω
Può anche variare sinusoidalmente B invece di girare S.
3.2 BETATRONE
Appartiene alla famiglia degli acceleratori circolari.
Il campo B ha più funzioni:
1. Guida gli e- su orbite circolari
2. Essendo variabile sinusoidalmente genera E che accelera gli e3. Mantiene costante il raggio dell’orbita.
4. Introduce ed estrae gli e- quando hanno EK finale adeguata
mv 2
mv
= evB
r=
( m = γm0 )
r
eB
N
S
Per mantenere r costante deve essere v/B costante. Quindi al crescere di v deve crescere B.
Si usa B sinusoidale (frequenza tipica 50 Hz). Alla fine del primo T/4, B diminuisce, FLorentz diminuisce e
Φ(B) V=-dΦ/dt
t
così aumenta il raggio di curvatura: e- entra in una regione schermata da B e parte tangenzialmente.
3.3 CORRENTI PARASSITE
Nell’estrazione di una lastra conduttrice da un campo magnetico
si formano correnti circolari che si oppongono al moto per attrazione o repulsione magnetica. In figura (Halliday per università) il campo della corrente è concorde con B esterno ed esercita
un’attrazione che richiede un lavoro aggiuntivo delle forze
esterne nell’estrarre la lastra.
Applicazioni delle correnti parassite (in inglese, eddy currents):
Pendolino di Waltenhofen – Freni elettrodinamici.
(cfr. videoclip sul sito)
classe 5 G
pagina 4
rev. 2016
Matematica e Fisica
Schema elettromagnetismo
4 INDUTTANZA
Se una spira a i1 variabile può produrre su una spira vicina una i2 indotta, non può una spira a i1 variabile produrre una i indotta su se stessa?
iind
i0
Bind
La risposta sta nel fatto che nella legge di F-N il flusso Φ è il flusso totale che comprende anche gli effetti
della spira su se stessa (autoinduzione).
L’autoinduzione è una inerzia elettromagnetica causata dall’opposizione della f.e.m.∆indotta
sul circuito inB0
ducente.
Consideriamo un solenoide, all’interno del quale sappiamo calcolare B.
Il suo Φ è direttamente proporzionale a B e quindi a i:
Φ( B) = NBS = NµinS = µin 2lS = µin 2V = Li
L è l’induttanza, misurata in Henry (1 H = induttanza di un circuito in cui una corrente di 1 A produce un
flusso di B di 1 Wb).
In un solenoide L = µn2V
Per i circuiti, la legge di F-N si scrive più utilmente:
f .e.m. = − L
di
dt
4.1 CIRCUITO RL (CARICA)
V −L
di
= iR
dt
V = iR + L
ED
ENERGIA DEL CAMPO MAGNETICO
di
dt
R
Moltiplico per idt e ottengo energie:
Li (Φ)
L
V
Vidt = i Rdt + Lidi
2
E f .e.m. = E Joule + E L
i
Li
S=½Li
Quindi Lidi rappresenta energia magnetica immagazzinata in L.
2
di
ifinale
i
Il calcolo dell’energia W immagazzinata in L lavoro corrisponde al calcolo dell’area sotto la curva di
Φ(i)=Li in funzione di i:
t2
i2
W = ½ Li2
∫ Pdt = ∫ Lidi
t1
Per un solenoide:
W = 12 µn 2Vi 2

 B = µin
1 B2
W=
V
2 µ
1 B2
wm =
2 µ
W=
i1
1 2
Li
2
wm è la densità di energia magnetica (J/m3) immagazzinata nell’induttanza.
Un campo magnetico, come uno elettrico, è una forma di energia nello spazio
(dotata di un particolare tipo di potenziale, il potenziale vettore magnetico)
classe 5 G
pagina 5
rev. 2016
Matematica e Fisica
Schema elettromagnetismo
4.2 CIRCUITO RL (SCARICA)
di
= Ri
dt
R
i′ = − i
L
−L
i (0 ) = i0
i0
L
R
A
Qual è f(x) per cui y’ = ky ? È y = e kx
t
i = i0 e
R
− t
L
4.3 CIRCUITO R~
V0
In un circuito con sola resistenza in corrente alternata (R ~) la corrente segue la curva del la tensione.
~
A
i0
V0 sen(ωt + ϕ 0 ) = iR
i=
t
V0
sen(ωt + ϕ 0 ) = i0 sen(ωt + ϕ 0 )
R
L’energia dissipata per effetto Joule, L=i2Rdt, non cambia ma, definendola a parità di potenza dissipata con una corrente continua,
si introduce ieff =
i0
. Una corrente alternata di intensità massima
i02
i0 produce la stessa dissipazione termica di una corrente continua
di ieff.
i02/2
2
Infatti i2 cambia come in figura e ha interesse il suo valor medio.
 1 − cos 2ωt  1 2
2
 = i0
ieff
= i 2 = i02 sen 2 ωt = i02 
cos 2ωt = 0
2

 2
(
i0
)
t
4.4 TRASFORMATORE
Con la corrente alternata è più semplice trasformare correnti a tensioni diverse.
i1
i2
dΦ

N2 = i1VR1 V2

dt

dΦ
V2 = − N 2
dt

V1 ~ V1 −N1N1
Φ è il medesimo e R1 << V1/i1, quindi l’equazione dei trasformatori:
V2
N
=− 2
V1
N1
classe 5 G
pagina 6
rev. 2016
Matematica e Fisica
Schema elettromagnetismo
5 ONDE ELETTROMAGNETICHE
Ipotesi della corrente di spostamento di Maxwell.
Γ B=µ (i+ϵ
d ΦE
)
dt
Nel vuoto:
Γ B=
1 d ΦE
2
c dt
Maxwell scopre che il campo può avere esistenza indipendente dalle sue sorgenti, che può avere una esistenza tutta sua. E’ la fine della spazio vuoto della fisica classica.
Un esempio semplice di riduzione delle equazioni di Maxwell (onda piana):
2
E
∂ E
=εµ
2
2
∂x
∂t
∂
2
Le onde meccaniche in una direzione hanno equazione del tipo:
2
A 1
= 2
2
∂x
v
∂
2
A
2
∂t
∂
la cui soluzione è una equazione del tipo:
A( x , t)= A0 sin( kx − ω t +φ 0 )
E ( x , t )=E 0 sin( kx− ω t+ φ 0)
(v=c= ω )
k
Velocità
1
c= √ε µ
0
0
1
v= √εµ
Indice rifrazione
n=
c
= √εr µ r≃ √ε r
v
Le incongruenze sono dovute al fatto che n è valutato con 1015 Hz ed ε r (dei mezzi trasparenti) con campi
statici.
Densità di energia spaziale
1
wE= ε E2
2
wB=
1 B2 1 2
= εE
2 µ 2
wem =ε E 2 J / m ³
giacché: E = c B.
Ma poiché E è sinusoidale il valore efficace è ½ del valore di picco E0:
w em =
classe 5 G
1
2
ε E 0 [ J /m ³]
2
pagina 7
rev. 2016
Matematica e Fisica
Schema elettromagnetismo
Intensità di irraggiamento
Irraggiamento di una superficie S per un tempo Δt:
I=
w em V
W
1 ε0 2
=
= wem c =
E
S ∆t
S ∆t
2 µ0 0
√
Cfr. corpo nero, Planck 1899, ed effetto fotoelettrico, Einstein 1905: I = k f
I = w em c
[W /m ²]
Quantità di moto
E agisce sulle cariche presenti nello spazio muovendole nella sua direzione (se positive) e in direzione opposta (se negative). B agisce su tali cariche in movimento sempre con una forza nella direzione di propagazione: Δp = F Δt.
Sia per Maxwell nella teoria ondulatoria che poi per Einstein: q =
W
c
( E = p c [ J ])
Pressione
Per un onda piana che si propaga in una direzione la pressione esercitata sulla materia vale:
•
Contro uno schermo assorbente:
p=
•
w em
F
q
W
I
=
=
= =
S
S ∆t
c S∆t
c
c
(F =
∆q
q
=
)
∆t
∆t
(F =
∆q 2q
=
)
∆t
∆t
p = w em [ Pa ]
Contro uno schermo riflettente:
p=
wem
F
2q
2W
2I
=
=
=
=2
S
S ∆t
cS ∆t
c
c
p = 2 w em
[Pa ]
Esempio
Fuori atmosfera Costante solare I = 1.36 kW/m²
Sulla superficie terrestre ISole ≈ 1 kW/m² al massimo
Si ha una pressione solare:
p=
103
−6
= 3⋅ 10 Pa
8
3⋅ 10
Sul pianeta Terra agisce una forza:
F = p S = 3⋅ 10− 6⋅ π⋅ (6.3⋅ 106)2 = 4⋅ 108 N
classe 5 G
pagina 8
rev. 2016