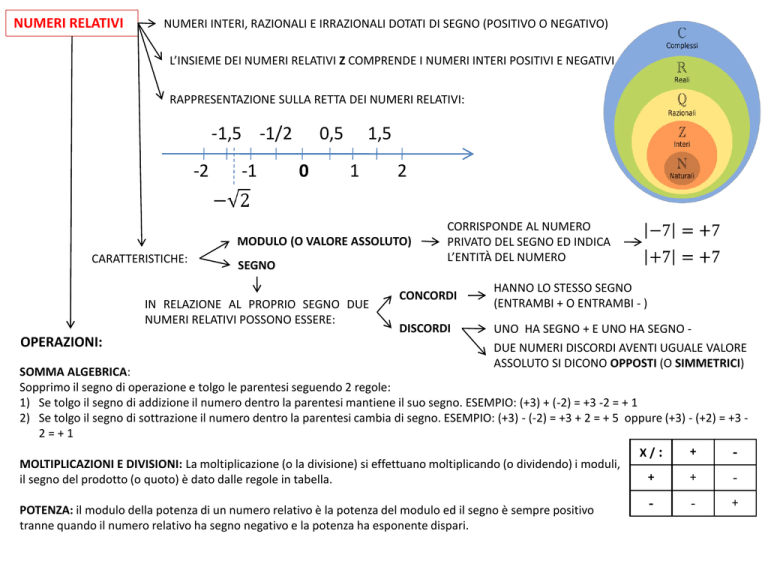
NUMERI RELATIVI
NUMERI INTERI, RAZIONALI E IRRAZIONALI DOTATI DI SEGNO (POSITIVO O NEGATIVO)
L’INSIEME DEI NUMERI RELATIVI Z COMPRENDE I NUMERI INTERI POSITIVI E NEGATIVI
RAPPRESENTAZIONE SULLA RETTA DEI NUMERI RELATIVI:
-1,5 -1/2
-2
-1
0,5
0
1,5
1
2
MODULO (O VALORE ASSOLUTO)
CARATTERISTICHE:
SEGNO
IN RELAZIONE AL PROPRIO SEGNO DUE
NUMERI RELATIVI POSSONO ESSERE:
OPERAZIONI:
CORRISPONDE AL NUMERO
PRIVATO DEL SEGNO ED INDICA
L’ENTITÀ DEL NUMERO
CONCORDI
DISCORDI
HANNO LO STESSO SEGNO
(ENTRAMBI + O ENTRAMBI - )
UNO HA SEGNO + E UNO HA SEGNO DUE NUMERI DISCORDI AVENTI UGUALE VALORE
ASSOLUTO SI DICONO OPPOSTI (O SIMMETRICI)
SOMMA ALGEBRICA:
Sopprimo il segno di operazione e tolgo le parentesi seguendo 2 regole:
1) Se tolgo il segno di addizione il numero dentro la parentesi mantiene il suo segno. ESEMPIO: (+3) + (-2) = +3 -2 = + 1
2) Se tolgo il segno di sottrazione il numero dentro la parentesi cambia di segno. ESEMPIO: (+3) - (-2) = +3 + 2 = + 5 oppure (+3) - (+2) = +3 2=+1
+
X/:
MOLTIPLICAZIONI E DIVISIONI: La moltiplicazione (o la divisione) si effettuano moltiplicando (o dividendo) i moduli,
+
+
il segno del prodotto (o quoto) è dato dalle regole in tabella.
POTENZA: il modulo della potenza di un numero relativo è la potenza del modulo ed il segno è sempre positivo
tranne quando il numero relativo ha segno negativo e la potenza ha esponente dispari.
-
-
+
IDENTITA’
UGUAGLIANZA DI DUE ESPRESSIONI (DI CUI ALMENO UNA LETTERALE) CHE È VERIFICATA DA QUALUNQUE VALORE
ATTRIBUITO ALLA LETTERA O ALLE LETTERE CHE VI FIGURANO.
ESEMPIO: 2x + x = 3x QUESTA SCRITTURA RISULTA VERA PER QUALUNQUE VALORE DI x (x=0,1,2,3,…)
EQUAZIONE
È UNA UGUAGLIANZA DI DUE ESPRESSIONI (DI CUI ALMENO UNA LETTERALE) VERIFICATA SOLO DA
PARTICOLARI VALORI ATTRIBUITI ALLA LETTERA O ALLE LETTERE CHE VI FIGURANO.
ESEMPIO: 4x + x = 10
QUESTA SCRITTURA RISULTA VERA SOLO PER x = 2 infatti 4 * 2 + 2 = 10
x2 – 1 = 2x + 2
1° MEMBRO
2° MEMBRO
LA LETTERA VIENE DETTA INCOGNITA (PERCHÉ BISOGNA TROVARE QUANTO VALE!)
NELL’ESEMPIO DI LATO è LA x
I TERMINI CHE NON CONTENGONO LETTERE SONO DETTI TERMINI NOTI
NELL’ESEMPIO DI LATO LO SONO: -1 E +2
IL GRADO DELL’EQUAZIONE è IL GRADO COMPLESSIVO DEL MONOMIO DI MASSIMO GRADO CHE VI COMPARE
NELL’ESEMPIO DI LATO IL MONOMIO DI MASSIMO GRADO È x2, QUINDI IL GRADO DELL’EQUAZIONE È 2.
I VALORI CHE RENDONO VERA L’EQUAZIONE SI DICONO RADICI DELL’EQUAZIONE.
IN QUESTO CASO LO È AD ESEMPIO IL VALORE +3 INFATTI: x2 – 1 = 32 – 1 = 8
EQUAZIONI EQUIVALENTI
E
2x + 2 = 2*3 + 2 = 8
SONO EQUAZIONI CHE HANNO LE STESSE SOLUZIONI.
ESEMPIO:
2x -3 = x
E
x + 14 = 5x + 2
ENTRAMBE RISULTANO SODDISFATTE PER x= 3
COME RISOLVERE
LE EQUAZIONI
TRASFORMO L’EQUAZIONE DI PARTENZA IN UN’ALTRA AD ESSA EQUIVALENTE DI SEMPLICE SOLUZIONE. PER
TRASFORMARLA MI SERVO DI DUE PRINCIPI DI EQUIVALENZA:
PRIMO PRINCIPIO DI EQUIVALENZA:
ADDIZIONANDO O SOTTRAENDO AD ENTRAMBI I MEMBRI DI UN’EQUAZIONE UNA STESSA ESPRESSIONE ALGEBRICA LETTERALE (O UNO
STESSO NUMERO) OTTENIAMO UN’EQUAZIONE EQUIVALENTE.
ESEMPIO:
PRENDIAMO 2X -3 = X CHE HA SOLUZIONE X=3.
AGGIUNGIAMO AD ENTRAMBI I MEMBRI +4 2X – 3 + 4 = X + 4
SOMMIAMO ALGEBRICAMENTE I TERMINI NOTI 2X + 1 = X + 4
QUEST’ULTIMA EQUAZIONE HA ANCORA SOLUZIONE X = 3.
CONSEGUENZE:
1) LA LEGGE DEL TRASPORTO: UN TERMINE PUÒ ESSERE PORTATO DAL PRIMO AL SECONDO MEMBRO (E VICEVERSA) SEMPLICEMENTE
CAMBIANDOLO DI SEGNO.
ESEMPIO: PRENDIAMO 2X -3 = 5 CHE HA SOLUZIONE X=4.
TRASPORTO -3 DAL PRIMO MEMBRO AL SECONDO MEMBRO CAMBIANDOLO DI SEGNO: 2X = 5 + 3, CALCOLO: 2X = 8 .
LA SOLUZIONE è ANCORA X=4
2) LA SOPPRESSIONE DI TERMINI UGUALI: SE IN ENTRAMBI I MEMBRI DI UN’EQUAZIONE CI SONO DUE TERMINI UGUALI, ESSI
POSSONO ESSERE SOPPRESSI.
ESEMPIO: PRENDIAMO 2X +3 = 6 +3 CHE HA SOLUZIONE X=3.
SOTTRAENDO AL PRIMO E AL SECONDO MEMBRO 3 OTTENIAMO: 2X = 6.
LA SOLUZIONE E’ ANCORA X=3
COME RISOLVERE
LE EQUAZIONI
TRASFORMO L’EQUAZIONE DI PARTENZA IN UN’ALTRA AD ESSA EQUIVALENTE DI SEMPLICE SOLUZIONE. PER
TRASFORMARLA MI SERVO DI DUE PRINCIPI DI EQUIVALENZA:
SECONDO PRINCIPIO DI EQUIVALENZA:
MOLTIPLICANDO O DIVIDENDO ENTRAMBI I MEMBRI DI UN’EQUAZIONE PER UNO STESSO NUMERO (DIVERSO DA ZERO) OTTENIAMO
UN’EQUAZIONE EQUIVALENTE A QUELLA DATA.
ESEMPIO:
PRENDIAMO 2X -3 = X CHE HA SOLUZIONE X=3.
MOLTIPLICHIAMO ENTRAMBI I MEMBRI PER 2 (2X – 3)*2 = X*2, VIENE: 4X – 6 = 2X
QUEST’ULTIMA EQUAZIONE HA ANCORA SOLUZIONE X = 3.
CONSEGUENZE:
1) IL CAMBIAMENTO DEI SEGNI: CAMBIANDO IL SEGNO AD OGNI TERMINE DI UN’EQUAZIONE OTTENIAMO UN’EQUAZIONE
EQUIVALENTE A QUELLA DATA.
ESEMPIO: PRENDIAMO L’EQUZIONE -2X=2. LA SOLUZIONE E’ X=-1 (INFATTI (-2)*(-1) = 2)
CAMBIANDO I SEGNI A TUTTI I TERMINI A PRIMO E A SECONDO MEMBRO OTTENGO: 2X=-2
ANCORA UNA VOLTA X=-1 E’ LA SOLUZIONE: 2(-1)=-2
2) LA RIDUZIONE A FORMA INTERA: SE L’EQUAZIONE CONTIENE DELLE FRAZIONI POSSO RIDURRE L’EQUAZIONE A TERMINI INTERI
MOLTIPLICANDO TUTTI I SUOI TERMINI PER IL m.c.m DI TUTTI I DENOMINATORI.
ESEMPIO: PRENDIAMO L’EQUZIONE 6/3X=1/2.
FACCIO IL MINIMO COMUNE MULTIPLO TRA I DENOMINATORI mcm(3;2)=6
RISCRIVO LE FRAZIONI CON QUESTO DENOMINATORE: 12/6X=3/6 .
PER IL SECONDO PRINCIPIO DI EQUIVALENZA MOLTIPLICO TUTTI I TERMINI PER UNO STESSO NUMERO (IN QUESTO CASO 6) E OTTENGO
ANCORA UN’EQUAZIONE EQUIVALENTE A QUELLA DATA: 12X=6 (CIOE’ UN’EQUAZIONE DI UGUALE SOLUZIONE). LA SOLUZIONE E’ X=1/2.
MONOMI
ESPRESSIONE LETTERALE CONTENENTE NUMERI E LETTERE LEGATE DALLA SOLA MOLTIPLICAZIONE. I NUMERI
(CON SEGNO) SONO DETTI COEFFICIENTI E LE LETTERE (CON ESPONENTE) SONO DETTE PARTE LETTERALE
MONOMI SIMILI: HANNO STESSA PARTE LETTERALE
MONOMI UGUALI: HANNO STESSA PARTE LETTERALE E STESSO COEFFICIENTE
MONOMI OPPOSTI-: HANNO STESSA PARTE LETTERALE E COEFFICIENTI OPPOSTI
(STESSI NUMERI E SEGNO OPPOSTO)
GRADO RELATIVO AD UNA LETTERA: E’ L’ESPONENTE CON CUI COMPARE QUELLA LETTERA NEL MONOMIO
GRADO COMPLESSIVO DEL MONOMIO: E’ LA SOMMA DEGLI ESPONENTI DELLE LETTERE DEL MONOMIO
POLINOMI
COSTITUITO DA PIU’ MONOMI LEGATI DA SOMMA ALGEBRICA (SOMMA O SOTTRAZIONE)
RIDOTTO: SE NON CONTIENE MONOMI SIMILI
BINOMIO: UN POLINOMIO RIDOTTO CONTENENTE 2 TERMINI
TRINOMIO: UN POLINOMIO RIDOTTO CONTENENTE 3 TERMINI
QUADRINOMIO: UN POLINOMIO RIDOTTO CONTENENTE 4 TERMONI E’ DETTO
COMPLETO RISPETTO AD UNA LETTERA: SE TALE LETTERA COMPARE CON TUTTI I SUOI GRADI DA QUELLO DI
GRADO MASSIMO A QUELLO DI GRADO ZERO.
ORDINATO RISPETTO AD UNA LETTERA: SE TALE LETTERA COMPARE NEL POLINOMIO CON ESPONENTI
DISPOSTI IN ORDINE (CRESCENTE: DAL PIU’ PICCOLO AL PIU’ GRANDE, O DECRESCENTE). NON IMPORTA CI
SIANO TUTTI I GRADI.
OMOGENEO SE TUTTI I MONOMI DEL POLINOMIO HANNO LO STESSO GRADO COMPLESSIVO
GRADO RELATIVO AD UNA LETTERA: E’ L’ESPONENTE CON CUI COMPARE QUELLA LETTERA NEL POLINOMIO
GRADO COMPLESSIVO DEL POLINOMIO: E’ IL MAGGIORE TRA I GRADI COMPLESSIVI DEI MONOMI CHE COMPONGONO IL POLINOMIO
POSSO SOMMARE SOLO MONOMI SIMILI TRA LORO
SOMMA
ALGEBRICA
DEI MONOMI SIMILI SOMMO SOLO LA PARTE DEI COEFFICIENTI E RISCRIVO SENZA MODIFICARLA LA PARTE LETTERALE.
ESEMPIO:
- 3 ab + 5 a2 – 2 ab – 2 a2 =
(cerco ed evidenzio i monomi simili) - 3 ab + 5 a2 – 2 ab – 2 a2 =
(sommo i coefficienti e riscrivo la parte letterale) = (- 3 – 2 ) ab + (5 – 2) a2 = (svolgo i conti) = – 5 ab + 3 a2
PRODOTTO
NON IMPORTA SE I MONOMI SONO SIMILI O MENO.
TRA DUE MONOMI: MOLTIPLICO I COEFFICIENTI E RISCRIVO TUTTE LE LETTERE PRESENTI NEI DUE MONOMI PRESE
UNA SOLA VOLTA CON ESPONENTE PARI ALLA SOMMA DEGLI ESPONENTI.
ESEMPIO:
- 3 ab * 5 a2 = (moltiplico i segni , poi i numeri e infine riscrivo tutte le lettere una sola volta
sommando gli esponenti) = (- *+) (3*5) a1+2b = - 15 a3b
TRA UN POLINOMIO E UN MONOMIO: MOLTIPLICO IL MONOMIO PER TUTTI I TERMINI DEL POLINOMIO
SEGUENDO LA REGOLA DELLA MOLTIPLICAZIONE TRA DUE MONOMI.
ESEMPIO:
- 3 ab * (5 a2 - 2bc) = (moltiplico il monomio per il primo termine e poi per il secondo termine del polinomio
mettendo SEMPRE tra le due moltiplicazioni il segno +) = (- 3 ab) * (5 a2) + (- 3 ab) * (- 2 bc) =
= (svolgo la moltiplicazione tra due monomi) (- *+) (3*5) a1+2b + (-*-) (3*2) (ab1+1c) = - 15 a3b + 6 ab2c
TRA DUE BINOMI: MOLTIPLICO CIASCUN TERMINE DEL PRIMO POLINOMIO PER TUTTI I TERMINI DEL SECONDO POLINOMIO
SEGUENDO LE REGOLE DELLA MOLTIPLICAZIONE TRA DUE MONOMI.
ESEMPIO:
( 2a + 3ab) * (5 a2 - 2bc) = (moltiplico il primo termine del primo binomio per il secondo binomio poi moltiplico il secondo
termine del primo binomio per il secondo binomio mettendo tra le due moltiplicazioni sempre il segno +)
= (2a ) * (5 a2 - 2bc) + (+ 3 ab) * (5 a2 - 2bc) = (svolgo la moltiplicazione monomio per binomio come il caso precedente)
= (2a) * (5 a2) + (2a) * (- 2 bc) + (+ 3 ab) * (5 a2) + (+3 ab) * (- 2 bc) = (svolgo la moltiplicazione tra due monomi)
= (+ *+) (2*5) a1+2 + (+*-) (2*2) (ab1+1c) + (+*+) (3*5) a1+2b + (+*-) (3*2) (ab1+1c) = +10 a3 - 4 abc +15 a3b - 6 ab2c
QUOZIENTE
NON IMPORTA SE I MONOMI SONO SIMILI O MENO.
TRA DUE MONOMI: DIVIDO I COEFFICIENTI E RISCRIVO TUTTE LE LETTERE PRESENTI NEI DUE MONOMI PRESE UNA
SOLA VOLTA CON ESPONENTE PARI ALLA DIFFERENZA DEGLI ESPONENTI.
ESEMPIO:
- 10 a4b : 5 a2 = (divido i segni , poi i numeri e infine riscrivo tutte le lettere una sola volta
sottraendo gli esponenti) = (- : +) (10*5) a4-2b = - 2 a2b
TRA UN POLINOMIO E UN MONOMIO: DIVIDO TUTTI I TERMINI DEL POLINOMIO PER IL MONOMIO
SEGUENDO LA REGOLA DELLA DIVISIONE TRA DUE MONOMI.
ESEMPIO:
(15 a2b – 6abc) : (- 3 ab) = (divido il primo termine del polinomio per il monomio e poi il secondo termine del
polinomio per il monomio mettendo SEMPRE tra le due divisioni il segno +) = (15 a2b) : (- 3 ab) + (- 6 abc) : (- 3 ab) =
= (svolgo la divisione tra due monomi) (+: -) (15*3) a2-1b1-1 + (-*-) (6*3) (a1-1b1-1c) = - 5 a1b0 + 2 a0b0c = - 5° + 2c
POTENZA
NON IMPORTA SE I MONOMI SONO SIMILI O MENO.
MONOMIO: LA POTENZA DI UN MONOMIO E’ UN MONOMIO CHE HA COME COEFFICIENTE LA POTENZA DEL
COEFFICIENTE E COME PARTE LETTERALE TUTTE LE LETTERE DEL MONOMIO PRESE UNA SOLA VOLTA CON ESPONENTI
PARI AL PRODOTTO DELL’ESPONENTE DELLA LETTERA PER L’ESPONENTE DELLA POTENZA.
ESEMPIO:
(- 3 a3b) 2 = (- 3)2 a3*2b1*2 = +9 a6b2
BINOMIO: PER FARE LA POTENZA DI UN BINOMIO DEVO MOLTIPLICARE IL BINOMIO PER SE STESSO
SEGUENDO LE REGOLE DELLA MOLTIPLICAZIONE DEI POLINOMI VISTE ALLA PAGINA PRECEDENTE OPPURE
POSSO APPLICARE LE FORMULE NOTE COME SEGUE:
ESEMPIO:
( 2a + 3b)2 = (2a)2 + (3b)2 + 2 * (2a) * (3b)
( 2a - 3b)2 = (2a)2 + (-3b)2 - 2 * (2a) * (3b)
(ATTENZIONE: la differenza è in un segno!)










