BREAK EVEN POINT
Il punto di pareggio in volumi: prima di considerare la teoria consideriamo un’esempio
per capire a cosa si riferisce bene il termine “punto di peggio”.
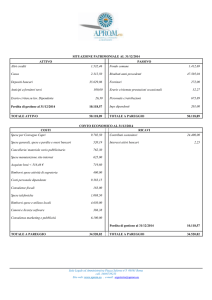
esmepio: prendiamo il caso di una panetterie e consideriamo che ci sono:
• Paga 700 affitto
• Paga 800 lavoro.
• Paga 300 pubblicità.
• Vende pane a 8 euro/kg.
• La farina costa 1 euro/kg di pane.
• Lieviti e altri ingredienti costano 2 euro/kg di pane.
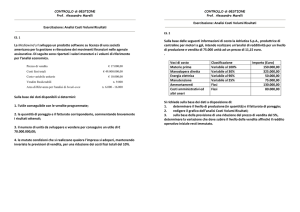
Quanti kg deve produrre e vendere il panettiere per non essere in perdita? Ogni kg di pane
ricava 8 euro, ma allo stesso tempo ogni kilo costa 2 euro + 1 euro, dunque il guadagno al
kg risulta essere 8-3=5 euro; questi 5 euro non sono però tutto utile perché deve pagare
l’affitto, la pubblicità e il lavoro. Quante volte deve dunque “mettere via 5 euro” per coprire
queste altre spese? il risultato è dato da (700+800+300)/5=360.
Questa questione nelle aziende è molto importante e si riferisce al punto di pareggio,
detto break even point, che esprime il valore o u la quantità tale per cui l’azienda ha un
utile pare a zero.
Parlando teoricamente possiamo dire che la determinazione del punto di pareggio è uno
degli elementi più importanti dell’analisi costi-volumi-risultati. Il punto di pareggio è
l’ammontare di vendite che consente di coprire tutti i costi aziendali. Il punto di pareggio
può essere inteso come il numero di pezzi da produrre e vendere per andare a pareggio
(punto di pareggio in volumi) o come fatturato da conseguire per andare a pareggio (punto
di pareggio in fatturato). Ora analizziamo l’ammontare di vendite che occorre conseguire
per coprire tutti i costi di gestione caratteristica, ossia il punto di pareggio operativo,
mentre dopo analizzeremo il punto di pareggio complessivo, da conseguire per coprire i
costi di gestione caratteristica, i costi finanziari e fiscali.
Vediamo i passaggi matematici che consentono di determinare i volumi di prodotto da
produrre e vendere per coprire tutti i costi di gestione caratteristica: Abbiamo detto che il
punto di pareggio (nella dimostrazione rappresentato da q) è rappresentato dal volume di
produzione per il quale i ricavi totali sono uguali ai costi totali di gestione caratteristica,
dunque scriviamo che:
RT (ricavi totali) = CT (costi totali) che è uguale a dire:
RT (ricavi totali) = CF (costi fissi) + CV (costi variabili)
ma sia i ricavi che i costi variabili totali dipendono dalla quantità prodotta, dunque
possiamo riscrivere entrambi come:
RVu x q = CF + (CVu x q)
dove Ru= ricavi unitari (prezzo del prodotto).
(RVu x q ) — (CVu x q) = CF
q( RVu — CVu ) = CF
CF
q =
Ru — CVu
La differenza tra ricavi unitari e costi variabili unitari viene comunemente denominata
margine di contribuzione unitario (MDCu).
Al fine di ottenere un indicatore relativo, è utile esprimere il margine di contribuzione in
percentuale dei ricavi (MDC%). Questo può essere ottenuto in due modi:
• Rapportando il margine di contribuzione unitario ai ricavi unitari (MDCu/Ru).
Il margine di contribuzione percentuale è utilizzato per calcolare il fatturato di pareggio
in valore, detto anche punto di pareggio in fatturato, che si identifica con il fatturato
minimo per non essere in perdita e che si utilizza quando nell’azienda ci sono più
prodotti.
Questo si calcola dividendo i costi fissi totali (CF) per il margine di contribuzione
espresso in percentuale dei ricavi (MDC%):
RP (ricavi di pareggio) = CF / mdc %
La versione in fatturato del punto di pareggio è molto utile in tutti i casi in cui non si
conoscono i costi unitari e nei casi in cui il concetto di quantità di pareggio non ha senso
in quanto l’azienda che si sta analizzando vende una gamma di prodotti e servizi molto
eterogenei.