INFINITO
ARTE & MATEMATICA
"Uno scienziato degno di questo nome, e soprattutto un matematico, prova lavorando
la stessa impressione di un artista; la gioia
che gli dà il suo lavoro è altrettanto grande
e della medesima natura" (H. Poincaré)
Creato da Alessandro & Annalisa
Maurits Cornelis Escher (17.06.1898– 27.03.1972)
È conosciuto principalmente per le sue incisioni su legno, litografie e
mezzetinte. Le sue opere hanno una forte componente matematica, e
molti dei mondi che ha disegnato sono costruiti attorno a oggetti impossibili come il Triangolo di Penrose oppure ad illusioni ottiche come
il Cubo di Necker. Le opere di Escher sono molto amate dagli scienziati, matematici, logici e fisici che apprezzano il suo uso di poliedri, distorsioni geometriche ed interpretazioni originali di concetti appartenenti alla scienza. Maurits Cornelis, o Mauk come venne soprannominato, nacque a Leeuwarden, nei Paesi Bassi, frequentò la Scuola di Architettura e Arti Decorative di Haarlem. Escher viaggiò molto e nel
gennaio 1941 si spostò a Baarn, in Olanda, dove visse fino al 1970. La
maggior parte dei disegni più famosi risalgono a questo periodo di tempo; il freddo, nuvoloso, umido clima olandese gli permise di concentrarsi interamente sul suo lavoro.
Autoreferenzialità, topologia, geometria iperbolica …
Le implicazioni logiche, matematiche, geometriche e fisiche sono
piuttosto variegate, e coinvolgono concetti come ad esempio:
1.
I processi ricorsivi, quali l'effetto Droste, collegati a particolari
rotazioni del piano, ad esempio in Galleria di stampe un visitatore,
guardando fuori da una finestra della galleria, rivede l'edificio
contenente anche se stesso, in una successione potenzialmente
infinita.
2.
L'infinito (sia filosofico che matematico), preludio alle geometrie
frattali a sviluppo infinito, in tutte le opere sul tema del limite
del cerchio, dove un motivo ripetitivo si espande nell'infinitamente piccolo.
3.
Tassellature degli spazi bi e tridimensionali, impieganti "tessere"
ripetute con tutte le possibili variazioni.
4.
Dischi di Poincaré, in litografie come Il limite del cerchio. Figure
simili sempre più piccole si susseguono all'infinito fino al bordo
esterno di un disco.
In tutte le opere non vi è solo la logica delle scienze esatte, ma mondi
naturali con panorami, scorci, piante ed animali reali o immaginari
che intervengono ad arricchire i suoi lavori in un'ottica straordinariamente globale.
Geometria iperbolica e …
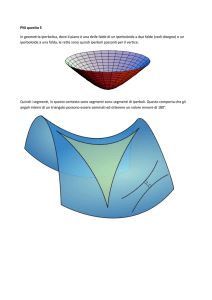
Nella geometria iperbolica, le rette parallele generalmente "divergono"
e gli angoli interni di un triangolo sono più piccoli che nella geome-
tria euclidea. Questo è quanto accade ad
esempio per le geodetiche su una superficie a forma di sella. Il Disco di Poincaré è
un modello di geometria iperbolica. Nella figura è descritta una tassellazione del
disco tramite triangoli iperbolici: nonostante appaiano diversi, nella geometria
iperbolica questi triangoli sono in realtà
tutti congruenti, cioè di eguale grandezza. A partire da tassellazioni di questo
tipo Escher ha costruito alcune delle sue
famose litografie.
Nell’ opera Cerchio limite III
La differenza tra la geometria iperbolica e quella euclidea è contenuta
nel V postulato delle parallele di Euclide: data una retta r ed un punto P
fuori da essa, esiste un'unica retta parallela a r passante per P.
La geometria iperbolica è la geometria ottenuta modificando questo
postulato, nel modo seguente:
Data una retta r e un punto P disgiunto da r, esistono almeno due rette
distinte passanti per P e parallele a r.
Uno spazio su cui è costruita una geometria iperbolica è detto spazio
iperbolico. I primi 4 assiomi di Euclide, validi in tutte le geometrie,
sono i seguenti.
1. Tra due punti qualsiasi è possibile tracciare una ed una sola retta.
2. Si può prolungare una retta oltre i due punti indefinitamente.
3. Dato un punto e una lunghezza, è possibile descrivere un cerchio.
4. Tutti gli angoli retti sono uguali.
Modello dell’iperboloide
Nel modello dell'iperboloide lo spazio iperbolico è un iperboloide contenuto nello spazio
tridimensionale, e le rette sono le intersezioni dell'iperboloide con un piano passante
per il centro dell'iperboloide. La descrizione matematica di questo modello ha forti
analogie con lo spaziotempo di Minkowski:
la distanza fra due punti è la stessa usata
nella relatività speciale.