Liceo Lugano 1, 2011-2012
3N (Luca Rovelli)
Capitolo II:
Geometria analitica nello spazio
1. Convenzioni e idee fondamentali
Grazie all’introduzione degli assi cartesiani Ox, Oy e Oz, lo spazio tridimensionale viene
identificato con lo spazio cartesiano
R3 = {(x, y, z)|x, y, z ∈ R} .
Ad ogni punto P dello spazio corrisponde esattamente una terna ordinata di numeri reali
(xP , yP , zP ) (l’ascissa, l’ordinata e la quota di P ). Per indicare il punto P di coordinate
xP , yP , zP scriveremo semplicemente P (xP , yP , zP ).
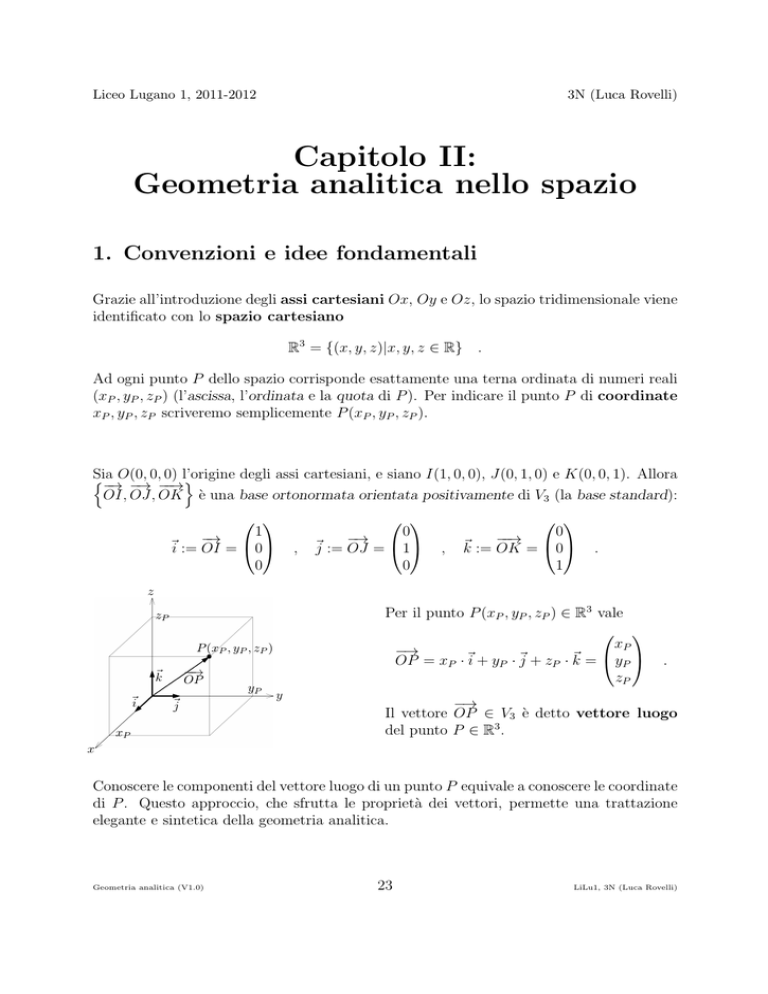
Sia
0, 0) l’origine degli assi cartesiani, e siano I(1, 0, 0), J(0, 1, 0) e K(0, 0, 1). Allora
n−→O(0,
−→ −−→o
OI, OJ, OK è una base ortonormata orientata positivamente di V3 (la base standard):
1
→
~i := −
OI = 0
0
,
0
→
~j := −
OJ = 1
0
,
0
−→
~k := −
OK = 0
1
.
z
Per il punto P (xP , yP , zP ) ∈ R3 vale
xP
−→
OP = xP · ~i + yP · ~j + zP · ~k = yP
zP
zP
P (xP , yP , zP )
−−→
OP
~k
~i
~j
xP
yP
y
.
−→
Il vettore OP ∈ V3 è detto vettore luogo
del punto P ∈ R3 .
x
Conoscere le componenti del vettore luogo di un punto P equivale a conoscere le coordinate
di P . Questo approccio, che sfrutta le proprietà dei vettori, permette una trattazione
elegante e sintetica della geometria analitica.
Geometria analitica (V1.0)
23
LiLu1, 3N (Luca Rovelli)
Risolviamo ora alcuni problemi elementari della geometria analitica con l’aiuto dei
vettori:
−→
a) Dati i punti A(xA , yA , zA ) e B(xB , yB , zB ), scrivi il vettore AB in componenti:
Otteniamo immediatamente
x
x
−→ −−→ −→ B A
AB = OB − OA = yB − yA
zB
zA
xB − xA
−→
cioè AB = yB − yA
zB − zA
.
b) Determina le coordinate del punto medio del segmento AB, con A(xA , yA , zA ) e
B(xB , yB , zB ):
Otteniamo immediatamente
−−→
−→ −−→ −→ 1 −→
OM = OA + AM = OA + AB
2
1
(xA + xB )
xB − xA
xA
2
1
= yA + yB − yA = 12 (yA + yB )
2
1
zB − zA
zA
(z + zB )
2 A
cioè M 12 (xA + xB ), 12 (yA + yB ), 21 (zA + zB ) (le coordinate del punto medio sono
la media aritmetica delle coordinate degli estremi del segmento).
c) Determina la distanza |AB| tra i punti A(xA , yA , zA ) e B(xB , yB , zB ): si tratta evi−→
dentemente del modulo del vettore AB, quindi
−→ p
|AB| = AB = (xB − xA )2 + (yB − yA )2 + (zB − zA )2
.
d) Dati A(xA , yA , zA ), B(xB , yB , zB ) e C(xC , yC , zC ) determina l’ampiezza dell’angolo
[
(convesso) α = BAC:
Come abbiamo già osservato,
definizione di prodotto scalare segue
−→ −→
AB · AC
cos α = −→
−→
kABk · kACk
Geometria analitica (V1.0)
24
dalla
.
LiLu1, 3N (Luca Rovelli)
e) Determina l’area A di un triangolo ABC, dati i vertici A(xA , yA , zA ), B(xB , yB , zB )
e C(xC , yC , zC ): l’area del triangolo misura metà dell’area di un parallelogrammo i
−→ −→
cui lati rappresentano AB e AC:
otteniamo
C
A=
B
A
1
−→ −→
AB
×
AC
2
.
A
f ) Determina il volume V e l’altezza h di un tetraedro ABCD: il volume è pari a 16
−→ −→ −−→
del volume del parallelepipedo di spigoli AB, AC, AD, l’altezza (relativa alla base
ABC) è uguale all’altezza di tale parallelepipedo:
1 h−→ −→ −−→i
V = AB, AC, AD 6
,
h−→ −→ −−→i
AB, AC, AD h= −→ −→
AB × AC 2. L’equazione parametrica della retta in R3
Una retta r nello spazioè determinata
in modo univoco da un punto P0 (x0 , y0 , z0 ) su di
v1
essa e da un vettore ~v =v2 parallelo ad essa (un vettore direttore o direzionale di r).
v3
r
P0 (x0 , y0 , z0 )
~v
−−→
OP0
P (x, y, z)
−
−
→
OP
O
⇐⇒
⇐⇒
⇐⇒
⇐⇒
P (x, y, z) giace su r
−−→
P0 P e ~v sono collineari
−−→
esiste λ ∈ R : P0 P = λ · ~v
−→ −−→
∃λ ∈ R : OP − OP0 = λ · ~v
−→ −−→
∃λ ∈ R : OP = OP0 + λ · ~v
L’equazione vettoriale
−→ −−→
r : OP = OP0 + λ · ~v
oppure, in componenti,
x
x0
v1
r : y = y0 + λ · v2
z
z0
v3
−−→
è detta equazione parametrica della retta r. Al variare del parametro λ, OP0 + λ · ~v
percorre i vettori luogo di tutti i punti sulla retta r. Quindi, variando λ nell’espressione
in componenti si ottengono le coordinate P (x, y, z) di tutti i punti sulla retta r.
Geometria analitica (V1.0)
25
LiLu1, 3N (Luca Rovelli)
Un altro modo per descrivere la retta è il seguente:
x = x0 + λ · v1
r : y = y0 + λ · v2
z = z0 + λ · v3
(le equazioni parametriche della retta r).
Osservazione: in R3 non è possibile eliminare il parametro λ dal sistema per ottenere una
sola equazione in x, y, z. Quindi, nello spazio tridimensionale una retta non può essere
descritta da un’unica equazione: saremo costretti ad operare con le equazioni parametriche.
Esempi:
1) Determina un’equazione
parametrica della retta r passante per A(−1, 2, 3) e parallela
5
al vettore ~v = 3 .
−8
Possiamo scrivere immediatamente
−1
5
x
r : y = 2 +λ · 3
3
−8
z
| {z }
| {z } | {z }
−
−
→
OP
−→
OA
x = −1 + 5λ
oppure r : y = 2 + 3λ
z = 3 − 8λ
.
~v
Osservazione: come abbiamo notato sopra, ogni scelta del parametro λ fornisce un punto
della retta; ad es. per λ = 2 si ottiene il punto P (−1+2·5, 2+2·3, 3+2·(−8)) = (9, 8, −13)
e per λ = 0 si ottiene il punto A.
2) Determina un’equazione parametrica della retta s passante
per A(2, −1, 3) e B(4, 5, −1).
2
−→
Possiamo scegliere P0 = A(2, −1, 3) e ~v = AB = 6 , e quindi
−4
x
2
2
s : y = −1 + λ · 6
z
3
−4
x = 2 + 2λ
oppure s : y = −1 + 6λ
z = 3 − 4λ
.
Osservazione: l’equazione parametrica di una retta non è unica: in essa compaiono le
coordinate di un punto P0 ∈ r qualsiasi e le componenti di un vettore ~v k r qualsiasi.
Ad esempio: nell’es. 2) avremmo potuto scegliere P0 = B(4, 5, −1) e dimezzare il vettore
−→
AB ottenendo una differente parametrizzazione della retta:
x
4
1
s : y = 5 +λ · 3 .
z
−1
−2
| {z }
| {z }
−
−
→
OB
Geometria analitica (V1.0)
26
1 −→
AB
2
LiLu1, 3N (Luca Rovelli)
−→
−−→
Data una retta r : OP = OP0 + λ · ~v e un punto A(xA , yA , zA ), è facile verificare se A
giace su r:
−−→
• dal punto di vista geometrico: è sufficiente controllare se i vettori ~v e P0 A sono
collineari;
• dal punto di vista algebrico: è sufficiente controllare se il sistema di equazioni
xA
x0
v1
yA = y0 + λ · v2
zA
z0
v3
di tre equazioni nell’unica incognita λ è risolvibile oppure no (cioè se, isolando λ
nelle tre equazioni, non si ottengono contraddizioni).
x
1
4
Esempio: siano P (−5, −1, 6), Q(5, 4, 5) e s : y = 2 + λ · 2 .
z
3
−2
Verifica che P ∈ s e Q 6∈ s.
Per quanto riguarda P :
−5
1
4
−1 = 2 + λ · 2
6
3
−2
⇐⇒
−5 = 1 + 4λ
−1 = 2 + 2λ
6 = 3 − 2λ
⇐⇒
3
1
λ = 4 (−5 − 1) = − 2
λ = − 21 (−1 − 2) = − 23
λ = − 12 (6 − 3) = − 32
e quindi P ∈ s; per quanto riguarda, invece, Q:
4
1
−5
−1 = 2 + λ · 2
−2
3
6
⇐⇒
5 = 1 + 4λ
4 = 2 + 2λ
5 = 3 − 2λ
⇐⇒
λ = 1
λ=1
λ = −1
e quindi Q 6∈ s.
Come abbiamo già notato, l’equazione parametrica di una retta riduce la conoscenza di un
punto su di essa alla conoscenza del corrispondente valore del parametro λ. Ciò permette
a volte di riformulare un problema geometrico come un’equazione in λ.
Esempio: dati il punto Q(3, 9, 4) e la retta
x
−1
2
0 + λ · 2
r : y =
z
3
1
−→
determina le coordinate di un punto P ∈ r tale che P Q ⊥ r.
Geometria analitica (V1.0)
27
LiLu1, 3N (Luca Rovelli)
Sia ~v =
2
2
1
il vettore direttore di r; allora la condizione si traduce nella relazione
−→
~v · P Q = 0; dal momento che vale P (−1 + 2λ, 2λ, 3 + λ) otteniamo
3 − (−1 + 2λ)
4 − 2λ
−→
= 9 − 2λ
9 − 2λ
PQ =
4 − (3 + λ)
1−λ
e quindi la condizione conduce a
2
4 − 2λ
2 · 9 − 2λ = 0
⇐⇒
1
1−λ
8 − 4λ + 18 − 4λ + 1 − λ = 0
⇐⇒
9λ = 27
e quindi deve valere λ = 3, da cui si ricava
P (−1 + 2 · 3, 2 · 3, 3 + 3) = P (5, 6, 6) .
3. La posizione reciproca di due rette
Due rette in R3
−→ −−→
r : OP = OP0 + λ · ~v
−→ −−→
e s : OP = OP1 + µ · w
~
possono essere tra loro coincidenti, parallele, incidenti oppure sghembe.
• Se i vettori direttori ~v e w
~ sono collineari, allora r e s sono coincidenti oppure
parallele:
– le due rette coincidono (”sono la stessa retta”) se P0 giace su s oppure P1 giace
su r (ricorda che l’equazione parametrica di una retta non è unica, e quindi
due equazioni parametriche diverse possono anche descrivere la stessa retta!),
– in caso contrario, quindi se P0 6∈ s oppure P1 6∈ r, le rette sono parallele.
Rette parallele
Rette coincidenti
Geometria analitica (V1.0)
28
LiLu1, 3N (Luca Rovelli)
• Se ~v e w
~ non sono collineari, le rette sono incidenti oppure sghembe. Per determinare
la posizione reciproca di r e s possiamo studiare il sistema di tre equazioni
x0 + λ · v1 = x1 + µ · w1
−−→
−−→
OP0 + λ · ~v = OP1 + µ · w
~ cioè, in componenti
y0 + λ · v2 = y1 + µ · w2
z0 + λ · v3 = z1 + µ · w3
v1
=v2
v3
in due incognite λ, µ, con P0 (x0 , y0 , z0 ), P1 (x1 , y1 , z1 ), ~v
w1
=w2 ;
w3
ew
~
– se il sistema possiede una una sola soluzione (λ0 , µ0 ), le rette si intersecano
in un punto I, le cui coordinate possono essere ricavate sostituendo λ = λ0
nell’equazione parametrica di r oppure µ = µ0 nell’equazione parametrica di s:
I(x0 + λ0 · v1 , y0 + λ0 · v2 , z0 + λ0 · v3 ) = I(x1 + µ0 · w1 , y1 + µ0 · w2 , z1 + µ0 · w3 );
– se il sistema non possiede soluzioni, cioè ad esempio se la soluzione (λ0 , µ0 )
ricavata dalle prime due equazioni non soddisfa la terza, le rette non hanno
punti in comune e pertanto sono sghembe.
Rette sghembe
Rette incidenti
Esempi: studia la posizione reciproca delle rette r e s:
x
2
1
x
−3
2
0 + µ · 1
1) r : y = −2 + λ · −1 , s : y =
z
5
1
z
1
1
Dal momento che i vettori direttori non sono collineari, le rette sono incidenti oppure
sghembe. Risolviamo quindi il sistema di equazioni
2
+
λ
=
−3
+
2µ
λ − 2µ = −5
⇐⇒
−λ − µ = 2
−2 − λ = µ
5+λ=1+µ
λ − µ = −4
Sommando le prime 2 equazioni otteniamo −3µ = −3, µ = 1 e dalla seconda
λ = −µ − 2 = −3. Dal momento che la soluzione (−3, 1) soddisfa anche la terza
equazione, il sistema è determinato, con S = {(−3, 1)}. Le rette sono incidenti nel
punto
I(2 + (−3), −2 − (−3), 5 + (−3)) = I(−1, 1, 2) .
Geometria analitica (V1.0)
29
LiLu1, 3N (Luca Rovelli)
x
2
1
x
3
−2
2) r : y = 1 + λ · −3 , s : y = 4 + µ · 6
z
3
−2
z
5
4
I vettori direttori sono collineari; pertanto, le rette sono parallele oppure coincidenti.
Controlliamo se il punto P0 (2, 1, 3) giace su s, risolvendo il sistema
1
2
=
3
−
2µ
µ = 2
⇐⇒
µ = − 12
1 = 4 + 6µ
µ = − 12
3 = 5 + 4µ
Evidentemente, il sistema non ha soluzioni e quindi le rette r e s sono parallele.
x
−4
3
x
2
1
y
5
1
y
0
3) r :
=
+λ·
,s :
=
+ µ · 3
z
1
1
z
3
1
Le due rette sono sghembe (verifica: per esercizio).
4. Angoli, proiezioni e distanze
Angolo tra due rette: l’angolo acuto tra due rette incidenti è definito in maniera
evidente. L’angolo tra due rette sghembe r e s è definito come l’angolo tra r e una
(qualsiasi) retta s0 parallela a s con r e s0 incidenti.
Rette sghembe
Rette incidenti
In entrambi i casi, quindi, l’angolo tra due rette
−→ −−→
r : OP = OP0 + λ · ~v
−→ −−→
e s : OP = OP1 + µ · w
~
:
è l’angolo acuto α tra le direzioni di ~v e w.
~
Grazie alla formula per l’angolo tra due vettori ricaviamo immediatamente
cos α =
|~v · w|
~
k~v k · kwk
~
Il valore assoluto garantisce che si tratti dell’angolo acuto: in effetti, per l’angolo supplementare ad α vale cos(π − α) = − cos α e quindi | cos(π − α)| = cos α.
In particolare, le due rette sono perpendicolari se e soltanto se ~v · w
~ = 0.
Geometria analitica (V1.0)
30
LiLu1, 3N (Luca Rovelli)
−→ −−→
Proiezione ortogonale: data una retta r : OP = OP0 +λ~v e un punto Q(xQ , yQ , zQ ) 6∈ r,
la proiezione ortogonale Q0 di Q su r è il punto Q0 ∈ r avente distanza minima da Q.
−−→
−−→
Dal momento che vale ~v ⊥ Q0 Q, è chiaro che ~v · Q0 Q = 0.
−−→
Dato che Q0 ∈ r, deve valere P0 Q0 = λ · ~v per un certo
λ. Inoltre osserviamo che
−−0→ −−→ −−→0 −−→
Q Q = P0 Q − P0 Q = P0 Q − λ · ~v .
−−→
Dalla condizione ~v · Q0 Q = 0 otteniamo un’equazione per λ:
−−→
−−→
~v · P0 Q − λ · ~v = 0
⇐⇒ ~v · P0 Q − λ ~|{z}
v · ~v = 0
⇐⇒
−−→
λk~v k2 = ~v · P0 Q
k~v k2
−−→
~v · P0 Q
. Infine sostituiamo tale valore di λ nell’equazione parada cui ricaviamo λ =
k~v k2
metrica di r per ricavare le coordinate di Q0 :
−−→
−−→0 −−→ ~v · P0 Q
· ~v
OQ = OP0 +
k~v k2
.
Esempio: determina le coordinate
della
proiezione
ortogonale di Q(3, 2, 3) sulla retta di
x
1
1
equazione parametrica r : y = 2 + λ 1.
z
3
1
Con la formula appena dimostrata otteniamo
3−1
1
1 · 2 − 2
5
−−→
1
1
1
1
3
−−→0 −−→ ~v · P0 Q
1
3−3
2 +
1 = 2 + 2 1 =
OQ = OP0 +
·
~
v
=
·
83
k~v k2
12 + 12 + 12
3
11
3
1
3
1
3
e quindi Q0 35 , 83 , 11
.
3
−→ −−→
Distanza punto-retta: la distanza tra un punto Q ∈ R3 e una retta r : OP = OP0 + λ~v
è la distanza minima tra Q e un punto di r:
dist(Q, r) = min {|QP | | P ∈ r}
.
Vediamo due modi per calcolarla:
Geometria analitica (V1.0)
31
LiLu1, 3N (Luca Rovelli)
Primo modo: la distanza tra Q e r è la distanza tra Q e la sua proiezione ortogonale Q0
su r. Conoscendo Q0 , il calcolo è quindi immediato:
−−→
dist(Q, r) = |QQ | = QQ0 0
.
x
1
1
Esempio: determina la distanza tra la retta r : y = 2 + λ 1 e il punto
z
3
1
Q(3, 2, 3).
(v. sopra).
Abbiamo già ricavato le coordinate della proiezione ortogonale: Q0 35 , 38 , 11
3
Quindi vale
5
−
3
−−→ 2 −2 2 √
38
2√
0
=
4+1+1=
6 .
dist(Q, r) = QQ = 3 − 2 = 1
3
3
11 − 3 3
1
3
−−→
Secondo modo: si tratta dell’altezza del parallelogrammo avente lati ~v e P0 Q rispetto
alla base ~v :
−−→
L’area di tale parallelogrammo misura k~v × P0 Qk.
Quindi
−−→
k~v × P0 Qk
dist(Q, r) =
.
k~v k
x
1
1
Esempio: (v. sopra) r : y = 2 + λ 1 , Q(3, 2, 3).
z
3
1
Calcoliamo
1
0 3
−
1
1 × 2 − 2
2
√
−−→
1
−2 3−3 k~v × P0 Qk
8
2√
dist(Q, r) =
=
= = √ =
6 .
1 1 k~v k
3
3
1
1
1 1 Geometria analitica (V1.0)
32
LiLu1, 3N (Luca Rovelli)
Distanza tra due rette r e s: si tratta della distanza minima tra un punto di r e un
punto di s, cioè
dist(r, s) = min {|P Q| | P ∈ r, Q ∈ s} .
Osservazione: se r k s, dist(r, s) è la distanza tra r e un punto qualsiasi di s (oppure
tra s e un punto qualsiasi di r).
−→
−−→
−→
−−→
Supponiamo ora che r : OP = OP0 + λ~v e s : OP = OP1 + µw
~ non siano parallele.
Allora, dist(r, s) è uguale alla distanza tra il piano parallelo a r e contenente s e il piano
parallelo a s contenente r. Si tratta dell’altezza del parallelepipedo avente spigoli ~v , w
~ e
−−→
P0 P1 rispetto alla faccia avente ~v e w
~ come lati.
La distanza d è pari al quoziente tra il volume e
l’area di base del parallelepipedo:
dist(r, s) =
h−−→
i
~ P0 P1 , ~v , w
k~v × wk
~
.
5. L’equazione parametrica del piano in R3
Un piano α nello spazio tridimensionale è determinato
in
maniera univoca da un punto
v1
w1
v3
w3
P0 (x0 , y0 , z0 ) su di esso e da due vettori ~v =v2 e w
~ =w2 non collineari ad esso paralleli.
P (x, y, z)
~v
⇐⇒
P0 (x0 , y0 , z0 )
w
~
−−→
OP0
α
−
−
→
OP
⇐⇒
⇐⇒
⇐⇒
P (x, y, z) giace sul piano α
−−→
P0 P , ~v e w
~ sono complanari
−−→
∃λ, µ ∈ R : P0 P = λ · ~v + µ · w
~
−→ −−→
∃λ, µ ∈ R : OP − OP0 = λ · ~v + µ · w
~
−→ −−→
∃λ, µ ∈ R : OP = OP0 + λ · ~v + µ · w
~
O(0, 0, 0)
L’equazione
−→ −−→
α : OP = OP0 + λ · ~v + µ · w
~
risp.
x
x0
v1
w1
α : y = y0 + λ · v2 + µ · w2
z
z0
v3
w3
è l’equazione parametrica (vettoriale) del piano α. Al variare dei parametri λ e µ,
−−→
OP0 + λ · ~v + µ · w
~ percorre i vettori luogo di tutti i punti di α. Quindi, variando λ e
µ nell’espressione in componenti si ottengono le coordinate P (x, y, z) di tutti i punti sul
piano α.
Geometria analitica (V1.0)
33
LiLu1, 3N (Luca Rovelli)
Un altro modo per descrivere il piano è il seguente:
x = x0 + λ · v1 + µ · w1
α : y = y0 + λ · v2 + µ · w2
z = z0 + λ · v3 + µ · w3
(le equazioni parametriche del piano α).
Esempio: determina l’equazione parametrica del piano passante per i punti A(3, 0, 6),
B(6, −6, −4) e C(8, 4, 8).
3
5
−→
−→
Possiamo scegliere P0 = A, ~v = AB = −6 e w
~ = AC =4, ottenendo
−10
2
3
3
5
x
α : y = 0 +λ · −6 +µ · 4
6
2
−10
z
| {z }
| {z }
| {z } | {z }
−
−
→
OP
−−→
OP0
~v
x = 3 + 3λ + 5µ
oppure α : y = −6λ + 4µ
z = 6 − 10λ + 2µ
.
w
~
Osservazioni:
(i) Come abbiamo menzionato in precedenza, ogni scelta dei parametri λ e µ fornisce
un punto del piano. Nell’esempio appena svolto, con λ = 1 e µ = −1 ricaviamo il
punto
P (3 + 3 · 1 + 5 · (−1), −6 · 1 + 4 · (−1), 6 − 10 · 1 + 2 · (−1)) = P (1, −10, −6)
del piano α.
(ii) come già per la retta, l’equazione parametrica di un piano non è unica, dal momento
che la sua forma dipende dalla scelta di P0 , ~v e w.
~
6. L’equazione cartesiana del piano in R3
Eliminando i parametri λ e µ dal sistema di equazioni
x = x0 + λ · v1 + µ · w1
α : y = y0 + λ · v2 + µ · w2
z = z0 + λ · v3 + µ · w3
si ottiene una sola equazione in x, y, z che può essere scritta nella forma
α : ax + by + cz + d = 0
con a, b, c, d ∈ R, l’equazione cartesiana del piano.
Geometria analitica (V1.0)
34
LiLu1, 3N (Luca Rovelli)
Esempio: determina l’equazione cartesiana del piano passante per i punti A(3, 0, 6),
B(6, −6, −4) e C(8, 4, 8).
Abbiamo già ricavato le equazioni parametriche di α (v. pag 34):
x = 3 + 3λ + 5µ
α : y = −6λ + 4µ
;
z = 6 − 10λ + 2µ
dalla prima equazione ricaviamo λ = 31 (x−3−5µ). Sostituendo nelle 2 equazioni rimanenti
otteniamo
(
(
1
y = −2x + 6 + 14µ
(2x + y − 6)
µ = 14
⇐⇒
10
56
3
z = 16 − 3 x + 3 µ
µ = 56 10
x + z − 16
3
e uguagliando le due espressioni per µ:
1
3 10
(2x + y − 6) =
x + z − 16
14
56 3
⇐⇒
2x − 4y + 3z − 24 = 0 .
L’equazione cartesiana cercata è quindi α : 2x − 4y + 3z − 24 = 0.
Osservazione: l’equazione cartesiana rappresenta una condizione per l’appartenenza di
un punto P (x, y, z) al piano. Ad esempio, il punto P (1, −10, −6) (prodotto a pag. 34)
giace nel piano α studiato sopra perchè le sue coordinate soddisfano l’equazione cartesiana:
2 · 1 − 4 · (−10) + 3 · (−6) + 24 = 2 + 40 − 18 − 24 = 0 ,
mentre il punto P (1, 2, 3) non giace in α:
2 · 1 − 4 · 2 + 3 · 3 − 24 = 2 − 8 + 9 − 24 = −21 6= 0 .
Un altro modo per ricavare l’equazione cartesiana di
un piano α conoscendo
un punto
v1
w1
v3
w3
P0 (x0 , y0 , z0 ) su di esso e due vettori non collineari ~v =v2 e w
~ =w2 ad esso paralleli
è il seguente: sappiamo che
⇐⇒
⇐⇒
⇐⇒
P (x, y, z) giace sul piano α
−−→
P0 P , ~v e w
~ sono linearmente dipendenti
h−
i
−→
P0 P , ~v , w
~ =0
x − x0 v1 w1 y − y0 v2 w2 = 0 .
z − z0 v3 w3 L’equazione cartesiana del piano α può quindi
nante:
x − x0 v 1
α : y − y0 v2
z − z0 v3
Geometria analitica (V1.0)
35
essere ricavata con l’aiuto di un determiw1
w2
w3
=0
.
LiLu1, 3N (Luca Rovelli)
Esempio (v. sopra): determina l’equazione
cartesiana
del piano passante per il punto
3
5
−10
2
A(3, 0, 6), e parallelo ai vettori ~v = −6 e w
~ =4.
Calcoliamo il determinante:
x − x0 v1 w1 x − 3 3 5 y − y0 v2 w2 = y − 0 −6 4 = . . . = 28x − 56y + 42z − 336 .
z − z0 v3 w3 z − 6 −10 2 L’equazione cartesiana cercata può essere scritta nella forma
α : 28x − 56y + 42z − 336 = 0
oppure, dividendo per 14,
α : 2x − 4y + 3z − 24 = 0 .
Osservazione: dati 3 punti A(xA , yA , zA ), B(xB , yB , zB ), C(xC , yC , zC ) giacenti su un
piano α, l’equazione cartesiana α : ax + by + cz + d = 0 può anche essere ottenuta grazie
a considerazioni puramente algebriche: sapendo che le coordinate dei 3 punti devono soddisfare l’equazione, e che a, b, c, d sono determinati a meno di una costante moltiplicativa1 ,
possiamo porre ad esempio d = −1 e ottenere un sistema di equazioni in a, b, c
xA · a + yA · b + zA · c = 1
xB · a + yB · b + zB · c = 1
xC · a + yC · b + zC · c = 1
Esempio (v. sopra): siano A(3, 0, 6), B(6, −6, −4) e C(8, 4, 8).
Otteniamo il sistema di equazioni
3a + 6c = 1
6a − 6b − 4c = 1
8a + 4b + 8c = 1
1
, − 16 , 18 .
la cui soluzione è (a, b, c) = 12
1
L’equazione cartesiana ottenuta è α : 12
x − 16 y + 81 z − 1 = 0. Moltiplicando per 24
otteniamo di nuovo
α : 2x − 4y + 3z − 24 = 0 .
1
cioè: moltiplicando entrambi i termini dell’equazione per una costante non nulla, essa rimane valida
per i medesimi punti
Geometria analitica (V1.0)
36
LiLu1, 3N (Luca Rovelli)
7. La direzione normale ad un piano
Un piano α in R3 può anche essere determinato in modo univoco da un punto su di esso
e da una direzione perpendicolare (o normale) ad α. Perricavare
l’equazione cartesiana
a
di α si procede come segue: siano P0 (x0 , y0 , z0 ) ∈ α e ~n = b ⊥ α;
c
~
n
P (x, y, z)
P (x, y, z) giace sul piano α
−−→
−−→
~n ⊥ P0 P , cioè ~n · P0 P = 0
a
x − x0
b · y − y0 = 0
c
z − z0
ax + by + cz −(ax0 + by0 + cz0 ) = 0
{z
}
|
⇐⇒
P0 (x0 , y0 , z0 )
⇐⇒
α
⇐⇒
O(0, 0, 0)
d
−−→
Ponendo d := −(ax0 + by0 + cz0 ) = −~n · OP0 , otteniamo un’equazione cartesiana
α : ax + by + cz + d = 0 .
Esempio: determina
un’equazione cartesiana del piano α passante per P (−1, 0, 3) e per
1
pendicolare a ~n =1.
2
Possiamo scrivere immediatamente
1
x+1
α : 1 · y − 0 = 0 cioè α : x + y + 2z − 5 = 0 .
2
z−3
Applicazioni del vettore normale:
a) Ogni vettore collineare a ~n
a
= b
c
è perpendicolare al piano α : ax + by + cz + d = 0.
b) Angolo acuto ∠(α, β) tra due piani α e β:
Il disegno in sezione mostra che l’angolo
acuto φ = ∠(α, β) è uguale all’angolo acuto
tra i rispettivi vettori normali ~nα e ~nβ ; vale
quindi
|~nα · ~nβ |
cos φ =
k~nα k · k~nβ k
Esempio: determina l’angolo
tra ipiani
acuto
α : 2x−y+3 = 0 e β : x+y−6z = 0.
2
1
0
−6
I vettori normali sono ~nα =−1 e ~nβ = 1 . Vale quindi
|~nα · ~nβ |
|2 − 1|
1
cos φ =
=√ √ =√
k~nα k · k~nβ k
5 · 38
190
Geometria analitica (V1.0)
37
,
φ = arccos
1
√
190
∼
= 85, 84◦
.
LiLu1, 3N (Luca Rovelli)
c) Condizione di parallelismo tra due piani
α : ax + by + cz + d = 0 e β : a0 x + b0 y + c0 z + d0 = 0
:
i piani sono paralleli se e soltanto se i rispettivi vettori normali ~nα e ~nβ sono
collineari, cioè se esiste k ∈ R con
a0 = k · a ,
b0 = k · b ,
c0 = k · c .
Nota che, se inoltre vale d0 = k · d, le equazioni di α e β sono equivalenti e quindi i
piani α e β coincidono.
Esempio: i piani
1
1
1
α : x + y − z + 3 = 0 e β : 3x + 2y − z + 5 = 0
2
3
6
sono paralleli, mentre i piani
1
1
1
γ : x − y + z + 3 = 0 e δ : 2x − 2y + z + 12 = 0
2
2
4
sono coincidenti.
d) Angolo acuto ∠(α, r) tra una retta r e un piano α:
Il disegno in sezione mostra che l’angolo
acuto ψ = ∠(α, r) è complementare
all’angolo acuto φ = ∠(~n, r) tra la retta r
e il vettore ~n normale ad α, cioè
∠(α, r) + ∠(~n, r) = 90◦
Esempio: determina l’angolo acuto tra la retta r :
x
y =
z
1
−2
3
.
λ
e il piano α :
2x + 3y − z = 0.
Calcoliamo immediatamente l’angolo tra r e il vettore normale a α:
1
2 −2 · 3
3
−1 |~v · ~n|
1
√
√
∠(~n, r) = arccos
= arccos
= arccos = 60◦
k~v k · k~nk
2
14 · 14
ed otteniamo quindi ∠(α, r) = 90◦ − ∠(~n, r) = 30◦ .
Geometria analitica (V1.0)
38
LiLu1, 3N (Luca Rovelli)
e) Un ulteriore modo per determinare l’equazione cartesiana di unpiano
α conoscendo
v1
w1
v3
w3
~ =w2 ad
un punto P0 (x0 , y0 , z0 ) su di esso e due vettori non collineari ~v =v2 e w
esso paralleli: α è il piano passante per P0 e perpendicolare al vettore ~n = ~v × w.
~
Esempio: (v. pag. 36): determina l’equazione
cartesiana
del piano passante per il
3
5
−10
2
punto A(3, 0, 6), e parallelo ai vettori ~v = −6 e w
~ =4.
Calcoliamo
3
5
28
2
~n = ~v × w
~ = −6 × 4 = −56 = 14 −4
−10
2
42
3
.
Quindi
−→
~n · AP = 0
⇐⇒
2
x−3
−4 · y = 0
3
z−6
⇐⇒
2x − 4y + 3z − 24 = 0 .
L’equazione del piano è α : 2x − 4y + 3z − 24 = 0.
f ) Distanza punto-piano: dati un punto P (xP , yP , zP ) e un piano
−→ −−→
α : OP = OP0 + λ~v + µw
~ ,
possiamo sfruttare il fatto che la distanza dist(P, α) è pari all’altezza di un paral−−→
lelepipedo di spigoli ~v , w
~ e P0 P .
La distanza può pertanto essere ottenuta come quoziente tra volume e
area di base:
h−−→
i
~ P0 P , ~v , w
h = dist(P, α) =
k~v × wk
~
P
h
w
~
P0
~v
α
Dalla definizione di prodotto misto, tenendo conto del fatto che ~n = ~v × w
~ è normale
ad α, ricaviamo
h−−→
i
~ P0 P , ~v , w
k~v × wk
~
=
−−→
~ P0 P · (~v × w)
k~v × wk
~
=
−−→ P0 P · ~n
k~nk
=
−−→ −−→ OP − OP0 · ~n
k~nk
−−→
−−→ OP · ~n − OP0 · ~n
=
k~nk
.
Come abbiamo già notato (pag. 37),
se l’equazione cartesiana del piano è data da
a
−−→
α : ax + by + cz + d = 0 vale ~n = b , OP0 · ~n = −d e
c
xP
a
−→
OP · ~n = yP · b = axP + byP + czP
zP
c
Geometria analitica (V1.0)
39
.
LiLu1, 3N (Luca Rovelli)
Abbiamo quindi dimostrato che la distanza tra il punto P (xP , yP , zP ) e il piano
α : ax + by + cz + d = 0 è data dalla formula
dist(P, α) =
|a · xP + b · yP + c · zP + d|
√
a2 + b 2 + c 2
.
Esempio: determina dist(A, α) con A(5, 1, −1) e α : x − 2y − 2z + 4 = 0.
Ricaviamo immediatamente
|5 − 2 · 1 − 2 · (−1) + 4|
9
dist(A, α) = p
= =3 .
2
2
2
3
1 + (−2) + (−2)
8. Intersezione tra 2 piani
Siano
α : ax + by + cz + d = 0 e β : a0 x + b0 y + c0 z + d0 = 0
due piani in R3 . Nel paragrafo precedente (pag. 38) abbiamo già chiarito a quali condizioni
α e β sono paralleli oppure coincidenti. Supponiamo ora che α e β non siano né paralleli,
né coincidenti. Allora la loro intersezione è una retta r = α∩β; per ricavarne un’equazione
parametrica è sufficiente conoscere due punti dell’intersezione.
Per ricavare un punto dell’intersezione α ∩ β è sufficiente scegliere a caso il valore di una
delle tre variabili x, y, z, ottenendo un sistema di equazioni per le altre due2 .
Esempio: determina la retta d’intersezione dei piani
α : x − 2y + 2z − 1 = 0
e β : 2x − 3y − z + 2 = 0 .
Dapprima scelgo z = 0, vado cioè alla ricerca del punto di quota 0 su r (la prima traccia
di r); ottengo il sistema
(
x − 2y − 1 = 0
2x − 3y + 2 = 0
Sottraendo la II equazione dal doppio della I ottengo −y − 4 = 0, e quindi y = −4,
x = 2y + 1 = −7. Il primo punto è quindi Q(−7, −4, 0).
Analogamente, scegliendo x = 1 ricavo il punto R(1, 1, 1). Un’equazione della retta
−→ −→
−→
r = QR = α ∩ β è r : OP = OQ + λ · QR, cioè
x
1
8
r : y = 1 + λ · 5 .
z
1
1
2
geometricamente, ciò significa intersecare i 2 piani con un terzo piano parallelo a Oxy, Oxz oppure
Oyz
Geometria analitica (V1.0)
40
LiLu1, 3N (Luca Rovelli)
Osservazione: la retta r = α ∩ β è ortogonale ai vettori normali ~nα e ~nβ . Quindi,
~nα × ~nβ è un vettore direttore per r; anche questo fatto può essere sfruttato per ricavare
un’equazione per r.
Esempio. (v. sopra) con
1
~nα = −2
2
e
2
~nβ = −3
−1
otteniamo
1
2
8
~v = ~nα × ~nβ = −2 × −3 = 5
2
−1
1
;
conoscendo inoltre un punto di r (ricavabile come sopra) possiamo scrivere un’equazione
parametrica.
9. Intersezione retta/piano
Siano α un piano e r una retta, dati come segue:
x
x0
v1
α : ax + by + cz + d = 0 risp. r : y = y0 + λ · v2
z0
v3
z
.
Sostituendo le tre equazioni
x = x 0 + λ · v 1
y = y0 + λ · v2
z = z0 + λ · v3
nell’equazione di α si ottiene un’equazione nell’incognita λ; sia S l’insieme delle sue
soluzioni;
• se S = ∅, nessun valore di λ permette di produrre un punto di α con l’equazione
parametrica di r e pertanto r ∩ α = ∅ : la retta r e il piano α sono paralleli (cioè:
r giace su un piano parallelo a α).
• se S = R, cioè r ∩ α = r, l’equazione parametrica di r produce un punto di α per
ogni valore di λ. La retta r giace quindi nel piano α.
• se S = {λ0 } per un certo λ0 ∈ R, vale r ∩ α = {P0 } dove P0 è il punto su r
corrispondente a λ0 (cioè il punto ottenuto sostituendo λ = λ0 nell’equazione di r).
rkα
r⊆α
r ∩ α = {P0 }
Geometria analitica (V1.0)
41
LiLu1, 3N (Luca Rovelli)
Esempio: determina α ∩ r, con
x
7
2
α : 2x − 2y − z + 17 = 0 risp. r : y = 6 + λ · −1
z
3
−2
.
Sostituendo, ottengo l’equazione
2(7 + 2λ) − 2(6 − λ) − (3 − 2λ) + 17 = 0 ⇐⇒ 8λ + 16 = 0 ⇐⇒ λ = −2 ;
quindi S = {−2} e il punto d’intersezione è
P0 (7 + 2 · (−2), 6 + (−1) · (−2), 3 + (−2) · (−2)) = P0 (3, 8, 7) .
10. L’equazione cartesiana della sfera
Una sfera S nello spazio tridimensionale R3 è definita univocamente dal suo centro
C(xC , yC , zC ) e dalla misura r > 0 del suo raggio.
P (x, y, z)
S
r
C(xC , yC , zC )
⇐⇒
⇐⇒
⇐⇒
P (x, y, z) giace sulla sfera S di centro C e raggio r
|CP | = r
|CP |2 = r2
(x − xC )2 + (y − yC )2 + (z − zC )2 = r2
L’equazione
S : (x − xC )2 + (y − yC )2 + (z − zC )2 = R2
(1)
è l’equazione cartesiana della sfera S. Essa può anche essere riscritta nella forma
S : x2 + y 2 + z 2 + ax + by + cz + d = 0
(2)
con a, b, c ∈ R.
Esempio: determina l’equazione cartesiana della sfera S con C(1, −3, 5) e r = 7.
Otteniamo
S : (x − 1)2 + (y + 3)2 + (z − 5)2 = 49 ,
oppure anche
S : x2 + y 2 + z 2 − 2x + 6y − 10z − 14 = 0 .
Se la sfera è descritta da un’equazione del tipo (2), è sempre possibile determinarne centro
e raggio: il completamento dei quadrati permette infatti di risalire ad un’equazione del
tipo (1), in cui C e r sono immediatamente leggibili.
Geometria analitica (V1.0)
42
LiLu1, 3N (Luca Rovelli)
Esempio: determina centro e raggio della sfera di equazione
x2 + y 2 + z 2 − 2x + 8y − 4z − 4 = 0
.
Completando il quadrato otteniamo
⇐⇒
⇐⇒
x2 − 2x + y 2 + 8y + z 2 − 4z − 4 = 0
(x − 1)2 − 1 + (y + 4)2 − 16 + (z − 2)2 − 4 − 4 = 0
(x − 1)2 + (y + 4)2 + (z − 2)2 = 25
Quindi: centro C(1, −4, 2), raggio r = 5.
11. Il piano tangente ad una sfera
Sia S una sfera di centro C, e P0 (x0 , y0 , z0 ) un punto della sfera. Allora, il piano tangente
−−→
alla sfera nel punto P0 è il piano per P0 perpendicolare al vettore CP0 :
⇐⇒
⇐⇒
P (x, y, z) giace sul piano α tangente a S in P0
CP0 ⊥ P0 P
−−→ −−→
CP0 · P0 P = 0
−−→
In altre parole, ~n = CP0 è il vettore normale al piano tangente.
Esempio: determina un’equazione cartesiana del piano tangente alla sfera S di centro
C(1, −2, 3) e raggio r = 3 nel punto P0 (3, 0, z) con z minimo.
Determiniamo innanzitutto l’equazione cartesiana della sfera:
S : (x − 1)2 + (x + 2)2 + (x − 3)2 = 9 ,
e ricaviamo la quota di P0 : con x = 3 e y = 0 otteniamo
(3 − 1)2 + (0 + 2)2 + (z − 3)2 = 9
⇐⇒
(z − 3)2 = 1
⇐⇒
z − 3 = ±1
e quindi z = 4 oppure z = 2; dato che z dev’essere minimo, è quest’ultima la quota
cercata: P0 (3, 0, 2). Ricaviamo l’equazione del piano tangente α:
3−1
x−3
−−→ −−→
0 + 2 · y − 0 = 0
CP0 · P0 P = 0
⇐⇒
⇐⇒
2(x − 3) + 2y − (z − 2) = 0
2−3
z−2
e quindi l’equazione cartesiana cercata è α : 2x + 2y − z − 4 = 0.
Geometria analitica (V1.0)
43
LiLu1, 3N (Luca Rovelli)
12. Intersezioni
Intersezione sfera/retta: siano
x = x0 + λ · v1
2
2
2
S : x + y + z + ax + by + cz + d = 0 e r : y = y0 + λ · v2
z = z0 + λ · v3
una sfera risp. una retta in R3 . Sostituendo le equazioni parametriche della retta
nell’equazione della sfera otteniamo un’equazione quadratica per λ, le cui soluzioni ci
permettono di ricavare i punti d’intersezione.
Esempio: determina i punti d’intersezione tra la retta
x
4
3
r : y = 5 + λ · 2
z
7
5
√
e la sfera S di centro O e raggio 14.
L’equazione della sfera è S : x2 + y 2 + z 2 = 14; sostituendo, ricaviamo l’equazione
(4+3λ)2 +(5+2λ)2 +(7+5λ)2 = 14
λ2 +3λ+2 = 0
⇐⇒
⇐⇒
(λ+2)(λ+1) = 0
le cui soluzioni sono λ = −2 e λ = −1, a cui corrispondono i punti d’intersezione
I1 (−2, 1, −3) e I2 (1, 3, 2).
Osservazione: il discriminante ∆ dell’equazione quadratica permette di stabilire se la
retta interseca la sfera in 2 punti (2 soluzioni, ∆ > 0), è tangente (∆ = 0) oppure non
interseca la sfera (∆ < 0).
Intersezione sfera/piano: siano
S : x2 + y 2 + z 2 + ax + by + cz + d = 0 e α : Ax + By + Cz + D = 0
una sfera (raggio R, centro C) risp. un piano in R3 . Sia inoltre d = dist(C, α) la distanza
tra il punto C e il piano α. Per la posizione reciproca di S e α ci sono tre possibilità:
• se d > R , la sfera S e il piano α non si intersecano;
• se d = R , il piano α è tangente alla sfera nel punto P , che può essere ottenuto
intersecando α con la retta perpendicolare ad α passante per C.
√
• se d < R , l’intersezione S ∩ α è una circonferenza di raggio r = R2 − d2 , il
cui centro C0 può essere ottenuto intersecando α con la retta perpendicolare ad α
passante per C.
Geometria analitica (V1.0)
44
LiLu1, 3N (Luca Rovelli)
Disegno in sezione della situazione:
Esempi: studia la posizione reciproca della sfera
S : x2 + y 2 + z 2 − 4x − 4y − 4z − 88 = 0
e del piano α, con
1) α : 3x + 4y + 36 = 0 ;
2) α : 8x + 5y + 4z − 139 = 0 ;
3) α : x + y + 2z − 26 = 0 .
Determiniamo dapprima centro e raggio della sfera:
⇐⇒
⇐⇒
x2 + y 2 + z 2 − 4x − 4y − 4z − 88 = 0
(x − 2)2 − 4 + (y − 2)2 − 4 + (z − 2)2 − 4 − 88 = 0
(x − 2)2 + (y − 2)2 + (z − 2)2 = 102
quindi: raggio R = 10, centro C(2, 2, 2).
|3 · 2 + 4 · 2 + 36|
50
√
=
= 10 .
5
32 + 42
Quindi: d = R, e il piano è tangente alla sfera. Determiniamo il punto di tangenza
intersecando α con la retta
x
2
3
t : y = 2 + λ 4
z
2
0
1) Determiniamo la distanza tra C e il piano α: d =
passante per C e perpendicolare ad α. Sostituendo nell’equazione di α ricaviamo
3(2 + 3λ) + 4(2 + 4λ) + 36 = 0
⇐⇒
25λ + 50 = 0
⇐⇒
λ = −2 .
Sostituendo λ = −2 nell’equazione parametrica di r, concludiamo che la sfera S e
il piano α sono tangenti nel punto P (−4, −6, 2).
Geometria analitica (V1.0)
45
LiLu1, 3N (Luca Rovelli)
√
|8 · 2 + 5 · 2 + 4 · 2 − 139|
√
= 105 .
82 + 52 + 42
Quindi: d > R, e il piano e la sfera non si intersecano.
2) Determiniamo la distanza tra C e α: d =
√
|2 + 2 + 2 · 2 − 26|
√
= 3 6 . Quindi:
12 + 12 + 22
d < R, e il piano e la sfera
si
intersecano
in
una
circonferenza.
Il raggio di tale
√
√
√
2
2
circonferenza misura r = R − d = 100 − 54 = 46 unità. Determiniamo il
centro C0 intersecando α con la retta
x
2
1
t : y = 2 + λ 1
z
2
2
3) Determiniamo la distanza tra C e α: d =
passante per C e perpendicolare ad α. Sostituendo nell’equazione di α ricaviamo
(2 + λ) + (2 + λ) + 2(2 + 2λ) − 26 = 0
⇐⇒
6λ − 18 = 0
⇐⇒
λ=3 .
Sostituendo λ = 3 nell’equazione parametrica di r concludiamo che la sfera S√e il
piano α si intersecano in una circonferenza di centro C0 (5, 5, 8) e raggio r = 46
unità.
Intersezione sfera/sfera: siano
S1 : x2 + y 2 + z 2 + a1 x + b1 y + c1 z + d1 = 0
S2 : x2 + y 2 + z 2 + a2 x + b2 y + c2 z + d2 = 0
due sfere in R3 di raggio r1 risp. r2 . Sia d = |C1 C2 | la distanza tra i centri C1 di S1 e C2
di S2 . Per la posizione reciproca di S1 e S2 ci sono le seguenti possibilità:
• se d > r1 + r2 , le sfere non si intersecano, e sono esterne una all’altra;
• se d = r1 + r2 , le sfere sono tangenti esternamente; per determinare il punto di
tangenza si può intersecare una delle due sfere con la retta C1 C2 ;
• se |r1 − r2 | < d < r1 + r2 , le sfere si intersecano in una circonferenza; per determinarne centro e raggio possiamo procedere come segue: sottraendo un’equazione
dall’altra si ottiene l’equazione cartesiana
α : (a1 − a2 )x + (b1 − b2 )y + (c1 − c2 )z + (d1 − d2 ) = 0
del piano contenente tale circonferenza; a questo punto si può intersecare α con S1
oppure S2 ;
• se d = |r1 − r2 | , le sfere sono tangenti internamente; per determinare il punto di
tangenza si può (come sopra) intersecare una delle due sfere con la retta C1 C2 ;
• se d < |r1 − r2 | , le sfere sono una interna all’altra.
Geometria analitica (V1.0)
46
LiLu1, 3N (Luca Rovelli)
Disegno in sezione della situazione:
d > r1 + r2
d = r1 + r2
|r1 − r2 | < d < r1 + r2
d = |r1 − r2 |
d < |r1 − r2 |
Esempi: studia la posizione reciproca delle sfere S1 e S2 :
1) S1 : x2 + y 2 + z 2 − 4x + 6y − 23 = 0, S2 : x2 + y 2 + z 2 − 2x + 2z − 2 = 0;
2) S1 : x2 + y 2 + z 2 − 14x − 14y − 24z + 172 = 0, S2 : x2 + y 2 + z 2 − 4x − 4y − 4z − 88 = 0.
Soluzioni:
1) Determiniamo i centri e i raggi: completando i quadrati ricaviamo
S1 : (x − 2)2 + (y + 3)2 + (z − 0)2 = 62
S2 : (x − 1)2 + (y − 0)2 + (z + 1)2 = 22
Quindi: centri C1 (2, −3, 0) e C2 (1, 0, −1), raggi r1 = 6, r2 = 4. La distanza tra i 2
centri è pari a
p
√
d = (1 − 2)2 + (0 + 3)2 + (−1 − 0)2 = 11
√
e quindi vale 11 = d < |r1 − r2 | = 4: la sfera S2 è interna alla sfera S1 .
2) Determiniamo i centri e i raggi: completando i quadrati ricaviamo
S1 : (x − 7)2 + (y − 7)2 + (z − 12)2 = 70
S2 : (x − 2)2 + (y − 2)2 + (z − 2)2 = 102
√
Quindi: centri C1 (7, 7, 12) e C2 (2, 2, 2), raggi r1 = 70, r2 = 10. La distanza tra i
2 centri è pari a
p
√
d = (7 − 2)2 + (7 − 2)2 + (12 − 2)2 = 5 6
e quindi vale |r1 − r2 | < |{z}
d < r1 + r2 : le sfere si intersecano quindi in una circon| {z√ }
| {z√ }
√
10− 70
5 6
10+ 70
ferenza. Calcolando la differenza tra le equazioni delle sfere ricaviamo l’equazione
cartesiana del piano contenente l’intersezione:
(x2 + y 2 + z 2 − 14x − 14y − 24z + 172) − (x2 + y 2 + z 2 − 4x − 4y − 4z − 88) = 0
⇐⇒
−10x − 10y − 20z + 260 = 0
⇐⇒
x + y + 2z − 26 = 0
Quindi il piano cercato è α : x + y + 2z − 26 = 0. Abbiamo già intersecato tale
piano con la sfera S2 in √
precedenza (pag. 46), ottenendo una circonferenza di centro
C0 (5, 5, 8) e raggio r = 46.
Geometria analitica (V1.0)
47
LiLu1, 3N (Luca Rovelli)










