Genetica dei caratteri quantitativi

Genetica dei caratteri quantitativi
Caratteri quantitativi o metrici
Vengono descritti mediante quantità di una unità di
misura appropriata. Devono essere misurati
Caratteri a variabilità continua
In un gruppo di individui, variano tra un valore minimo
ed uno massimo assumendo tanti valori intermedi;
non sono individuabili gruppi nettamente distinti
Caratteri multifattoriali o poligenici
Sono sotto il controllo di una pluralità di geni
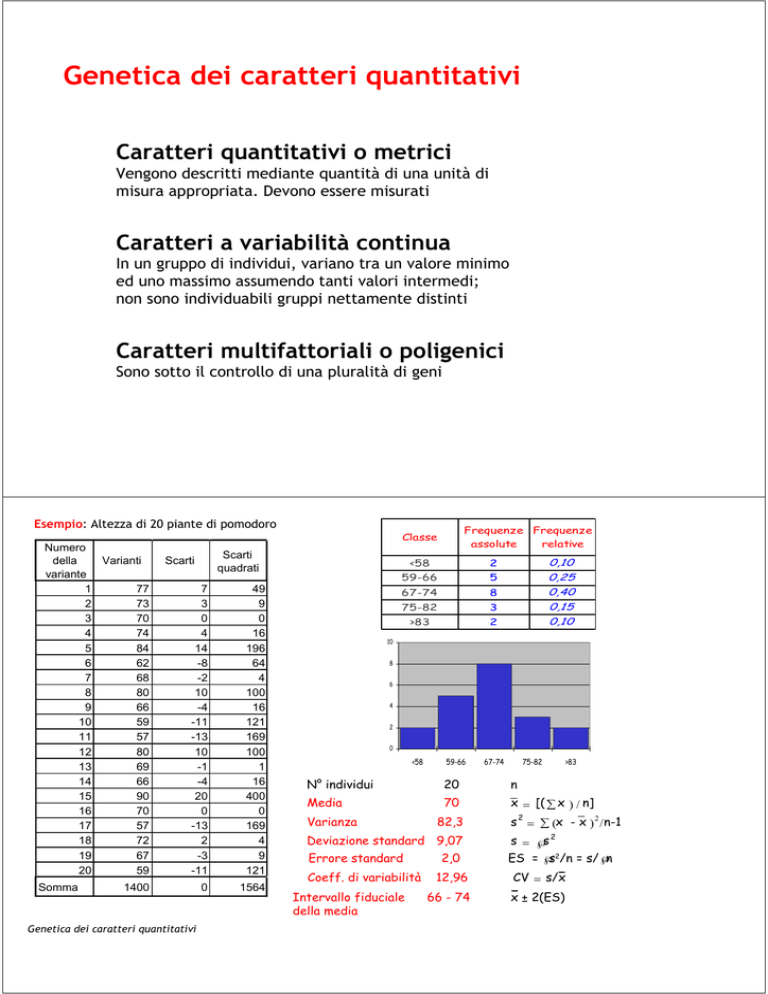
Esempio: Altezza di 20 piante di pomodoro
Frequenze Frequenze
relative
assolute
Classe
Numero
della
Varianti
variante
1
77
2
73
3
70
4
74
5
84
6
62
7
68
8
80
9
66
10
59
11
57
12
80
13
69
14
66
15
90
16
70
17
57
18
72
19
67
20
59
Somma
Scarti
quadrati
Scarti
7
3
0
4
14
-8
-2
10
-4
-11
-13
10
-1
-4
20
0
-13
2
-3
-11
49
9
0
16
196
64
4
100
16
121
169
100
1
16
400
0
169
4
9
121
0
1564
1400
Genetica dei caratteri quantitativi
<58
2
59-66
5
67-74
8
75-82
3
>83
2
0,10
0,25
0,40
0,15
0,10
10
8
6
4
2
0
<58
59-66
67-74
75-82
>83
N° individui
20
n
Media
70
x = [( ∑ x ) / n]
Varianza
82,3
Deviazione standard 9,07
Errore standard
Coeff. di variabilità
Intervallo fiduciale
della media
2,0
s 2 = ∑ (x - x ) 2 / n-1
s = √s2
ES = √s2/n = s/√n
12,96
CV = s/x
66 - 74
x ± 2(ES)
Istogrammi di frequenza
Classi fenotipiche
Frequenze relative
Frequenze relative
Distribuzione discontinua
Distribuzione continua
Classi fenotipiche
Frequenze relative
Genetica dei caratteri quantitativi
Genetica dei caratteri quantitativi
Classi fenotipiche
La curva normale
campionamento
POPOLAZIONE
PARAMETRI
STIME
inferenza
µ
σ
CAMPIONE
x
s
s
σ
µ
x
Genetica dei caratteri quantitativi
Popolazioni con la stessa media
e diverse deviazioni standard
σ
σ
µ
Genetica dei caratteri quantitativi
Esercitazione 1
Variabilità entro popolazioni e tra popolazioni
per un carattere quantitativo
Presso la serra sono presenti piantine di peperone di diverse varietà. Le varietà devono essere
distinguibili per motivi commerciali, e le caratteristiche morfologiche possono permettere di
distinguerle.
Vogliamo determinare la variabilità presente per la lunghezza delle foglie nelle singole varietà.
1. A coppie, misurate la lunghezza in mm della prima foglia di 50 piante prese a caso per
ciascuna popolazione.
2. Calcolate poi i parametri statistici della popolazione utilizzando Excel, senza utilizzare le
funzioni statistiche di excel, ma immettendo manualmente le formule (n, Media, Scarti dalla
media, Quadrati degli scarti, Somma delle varianti, Somma degli scarti, Somma dei quadrati
degli scarti, Varianza, Deviazione standard, Coefficiente di variazione, Errore standard,
Intervallo fiduciale della media.
3. Confrontare la variabilità delle diverse popolazioni.
4. Utilizzando excel, costruite un istogramma di frequenza raggruppando i dati in classi. Definite
voi le classi per una rappresentazione efficace della distribuzione della popolazione
Genetica dei caratteri quantitativi
La natura della variazione quantitativa
Il miglioramento genetico ha bisogno di variabilità genetica
Le leggi di Mendel spiegano la base della variazione genetica
qualitativa
fdzf
Dobbiamo conoscere la base genetica della variazione
quantitativa, quella più interessante sul piano pratico
Autofecondazione e omozigosi
F1
Aa
Generazioni
segreganti
F2
F3
¼ AA ½ Aa ¼ aa
AA
aa
%
omozigoti
%
eterozigoti
1
1/2
1/2
2
1/4
3/4
3
1/8
7/8
1/4
Aa
F4
1/8
Aa
F5
1/16
Aa
4
1/16
15/16
F6
1/32
Aa
5
1/32
31/32
m
1/2m
1-(1/2)m
1/8
1/8
Genetica dei caratteri quantitativi
Omozigosi
Autofecondazione e omozigosi
2m - 1
1-(1/2 ) =
m
Per n geni
(
2m
2m - 1
2m
)
n
1
n.
0,9
di geni
0,8
0,7
1
0,6
2
0,5
5
0,4
10
0,3
100
0,2
0,1
0
1
2
3
4
5
6
7
8
9
10
n. di generazioni segreganti (m)
Genetica dei caratteri quantitativi
11
12
Esperimento di
Johannsen
Fagiolo
Varietà
Princess
19
19
semi
semi
19
19
linee
linee
selezione dei
più leggeri
Autofecondazione
selezione dei
più pesanti
cg 64,3
cg 35,1
selezione dei
più leggeri
selezione dei
più pesanti
cg 35,8
cg 34,8
selezione dei
più leggeri
selezione dei
più pesanti
cg 63,1
cg 64,9
Genetica dei caratteri quantitativi
LINEA PURA
Insieme di individui
derivati per
autofecondazione
da un capostipite
omozigote
Genetica dei caratteri quantitativi
L'esperimento di Johannsen dimostra
per la prima volta che
la variabilità continua di un
carattere quantitativo è dovuta a
Cause genetiche
Cause ambientali
e
Rendono
la selezione
efficace
Possono
ostacolare
la selezione
s2P = s2G + s2E
Genetica dei caratteri quantitativi
Gli esperimenti di Nilsson-Ehle (1908)
Eredità del colore delle cariossidi in frumento
P1
F1
P2
F2
1)
rosso
x bianco
rosso
3 rossi
: 1 bianco
2)
rosso
x bianco
rosso
15 rossi
: 1 bianco
3)
rosso
x bianco
rosso
63 rossi
: 1 bianco
Se 1 coppia allelica controlla il carattere:
P
AA
F1
F2
x
AA
rosso
bianco
AA
rosso chiaro
1/4
AA
1/4 bianco
Genetica dei caratteri quantitativi
1/2
AA
1/4
3/4 rosso
AA
Se 2 coppie alleliche controllano il carattere:
AABB
P
x
bianco
AABB
rosso scuro
AABB
F1
rosso
F2
AABB
1/16
AABB
AABB
ecc.
AABB
AABB
ecc.
AABB
AABB
ecc.
AABB
4/16
6/16
4/16
1/16
0
1
2
1 bianco :
Genetica dei caratteri quantitativi
3
Gradi del colore
4
15 colorati
Se 3 coppie alleliche controllano il carattere:
x
AABBCC
P
AABBCC
rosso molto scuro
bianco
AABBCC
F1
F2
rosso scuro
AABBCC
AABBCC
Ecc..
AABBCC
AABBCC
AABBCC
Ecc..
AABBCC
AABBCC
Ecc..
AABBCC
AABBCC
Ecc..
AABBCC
AABBCC
Ecc..
AABBCC
20
15
15
6
6
1
0
1 bianco
Genetica dei caratteri quantitativi
1
1
2
:
3
4
63 colorati
5
6 Gradi del colore
1)
2)
3)
AABBCC x
AABBCC x
AABBCC x
AABBCC
AABBCC
AABBCC
L'esperimento di Nilsson-Ehle fornisce il primo modello della
eredità poligenica di un carattere “quantitativo”
Il fenotipo di un carattere quantitativo è sotto il
controllo di
Una pluralità di geni
Ambiente
Nilsson-Ehle (1908)
Johannsen (1906)
Genetica dei caratteri quantitativi
L'esperimento
di East (1916)
P2
P1
Carattere
Lunghezza della corolla
in Nicotiana longiflora
Specie strettamente
autogama
F1
n
Media
mm
Coeff. di
variabilità
P1
125
43,5
4,3
P2
88
93,2
2,5
F1
173
63,5
4,6
F2
211
67,5
8,8
Genetica dei caratteri quantitativi
F2
40
50
60
70
80
Lunghezza della corolla, mm
90
Se la lunghezza della corolla fosse controllata da 1 sola
coppia allelica East avrebbe dovuto osservare:
P
a1a1 x A1A1
F1
A1a1
a1a1
A1a1
A1a1
40
65
A = allele plus = 45 mm
a = allele minus = 20 mm
Differenza tra classi contigue
45 – 20 = 25 mm
Genetica dei caratteri quantitativi
Se la lunghezza della corolla fosse controllata da
2 coppie alleliche East avrebbe dovuto osservare:
P
a1a1a2a2 x A1A1A2A2
F1
A1a1A2a2
A = allele plus = 22,5 mm
a = allele minus = 10 mm
Genetica dei caratteri quantitativi
A1A1A2A2 = 90 mm
a1a1a2a2 = 40 mm
A1A1
90 mm
a1a1a2a2
A1a1a2a2
a1A1a2a2
a1a1A2a2
a1a1a2A2
A1A1a2a2
a1a1A2A2
A1a1A2a2
A1a1a2A2
a1A1A2a2
a1A1a2A2
40,0
52,5
65,0
2 coppie alleliche
A1A1A2a2
A1A1a2A2
A1a1A2A2
a1A1A2A2
A1A1A2A2
77,5
90,0
5 classi fenotipiche
Differenza tra classi contigue
22,5 – 10 = 12,5 mm
Genetica dei caratteri quantitativi
3 coppie alleliche
7 classi fenotipiche
4 coppie alleliche
9 classi fenotipiche
5 coppie alleliche
11 classi fenotipiche
A = allele plus = 9 mm; a = allele minus = 4 mm
Con 5 geni, le differenze tra classi contigue (9 - 4 = 5 mm) sono troppo
piccole per poter assegnare con sicurezza un individuo ad una classe
Genetica dei caratteri quantitativi
Risultati attesi nelle generazioni successive
1. Piante F2 con diversa lunghezza della corolla dovrebbero produrre famiglie F3
differenti per il carattere, poiché le differenze tra individui in F2 sono di natura
genetica e quindi ereditabili
F2
F3
2. In F3 la variabilità entro famiglia dovrebbe essere compresa tra quella
delle popolazioni parentali e F1 e quella della F2
3. Poiché l’autofecondazione porta all’omozigosi, la variabilità nelle
generazioni successive alla F2 dovrebbe essere uguale o inferiore a quella
della famiglia da cui è stata estratta la pianta madre.
Genetica dei caratteri quantitativi
Corolla pianta
madre (mm)
n
Media
Deviazione
standard
Coeff. di
variabilità
P1
-
125
43,5
1,8
4,3
P2
-
88
93,2
2,3
2,5
F1
-
173
63,5
2,9
4,6
F2
-
211
67,5
5,9
8,8
F3-1
46
143
53,5
3,7
7,0
F3-2
50
147
50,2
3,2
6,3
F3-3
82
162
80,2
4,8
5,9
F4-1-1
44
184
45,7
2,4
5,2
F4-2-1
43
189
46,3
1,9
4,0
F4-3-1
85
195
82,3
3,3
4,0
F5-2-1-1
41
161
42,0
2,3
5,5
IPOTESI MULTIFATTORIALE
Modello di Fisher, 1918
I caratteri quantitativi sono sotto il controllo di una pluralità di
geni mendeliani che agiscono additivamente (modello additivo)
L’effetto di ciascun gene è molto piccolo e non può essere seguito
individualmente (modello infinitesimale)
I geni che controllano un carattere quantitativo godono delle
stesse proprietà di quelli che controllano i caratteri qualitativi
(additività, dominanza, epistasi)
I caratteri quantitativi sono influenzati dalle condizioni ambientali
Genetica dei caratteri quantitativi
“Geneticists have for many years been aware that this model
is a simplification that does not accurately reflect the true
nature of biological systems. However, because the research
and commercial applications that adhered to this theory have
remained productive despite this, no major efforts have been
made to explore more biologically connected alternatives”
Nelson et al. 2013
A century after Fisher: time for a new paradigm in quantitative genetics Trends in Genetics-1090
E' possibile studiare e selezionare i caratteri quantitativi
come se fossere mendeliani ?
Sax (1923):
il colore del seme in fagiolo come marcatore per il peso
Thoday (1961): modello multi-marcatore per la selezione
Ad esempio:
Il gene G contribuisce al controllo di un carattere
quantitativo. L’allele G è quello utile.
Abbiamo incrociato due individui omozigoti
contrastanti per il carattere e abbiamo ottenuto
una popolazione segregante
G
M
g
m
1 cM
Se vogliamo selezionare l’allele G nella popolazione segregante, disporre di
marcatori molecolari (MM) associati strettamente ad esso ci permetterebbe di
selezionare direttamente il genotipo con grande precisione (in questo esempio,
gli individui che portano M portano anche G, con un errore dell’1%).
Se disponiamo di MM per tutti i geni che controllano il carattere quantitativo,
o per la maggior parte di essi, possiamo selezionarlo con facilità,
selezionando le combinazioni di alleli utili per tutti i MM.
Selezione assistita da marcatori (Marker-Assisted Selection, MAS)
Nuovi metodi per lo studio dei caratteri quantitativi
I loci che controllano caratteri quantitativi (Quantitaive Trait Loci,
QTL*) oggi possono essere individuati mediante l'aiuto di marcatori
molecolari che possono permettere di realizzare:
1. Mappaggio di QTL mediante mappe genetiche “classiche”:
2. Mappaggio “per associazione”, Association mapping o
Linkage disequilibrium (LD) mapping
Individuati nel genoma, con esperimenti di mappaggio, i QTL, per
lo meno quelli con gli effetti maggiori, diventa possibile la MAS.
Questa ha diverse modalità, tra cui la più avanzata è la
Selezione genomica (moduli Termolino e altri)
Mettiamo ora le basi di questi metodi
* Termine QTL introdotto da Geldermann, 1975 (TAG 46:319-330)
1. Mappaggio di QTL (for dummies)
Fase 1. In una popolazione segregante rilevo alcuni caratteri quantitativi (Q1, Q2...).
Costruisco una mappa di associazione di marcatori molecolari
Individui
popolazio
ne segregante
Marcatori (centinaia)
A
B
C
D
Car. quantitativi
...
Q1
Q2
(centinaia)
...
Marcatore A
Allele Media Q1
0
1
1
0
1
0
1
...
121
32
2
1
1
1
0
...
123
34
3
1
0
0
1
...
138
43
4
1
0
0
1
...
111
21
5
0
1
0
0
...
99
23
6
0
0
1
0
...
123
28
7
1
1
1
1
...
141
29
8
0
0
1
0
...
130
30
...
...
...
...
...
Nota: Questi 20 genotipi sono RIL!
Collard et al. 2005
118,25
145,00
Se la differenza tra i
due valori medi è
statisticamente
significativa (T-test, o
ANOVA, o regressione), il marcatore è
associato ad un QTL
che contribuisce a Q1
Mappaggio di QTL
Fase 2. Tra tutti i marcatori significativi, si selezionano marcatori indipendenti
mediante regressione multipla; otteniamo così il numero di regioni cromosomiche
indipendenti coinvolte nel controllo del carattere
Fase 3. Si rifà l’ANOVA con i soli marcatori indipendenti per determinare il loro effetto
singolo e cumulativo sulla varianza del carattere quantitativo e le eventuali interazioni
Si ottiene così una stima del numero minimo di loci, o regioni
cromosomiche, coinvolti e del loro “peso” nel determinare il carattere
Limitazioni
- Ci vogliono molti individui e molti marcatori
- QTL identificati in una determinata popolazione possono non essere
trovati in altre popolazioni
- QTL identificati in un determinato ambiente possono non essere trovati
in altri ambienti, anche nella stessa popolazione:
necessaria replicazione in più ambienti/anni
- E' difficile e costoso arrivare tanto vicino al gene da poterlo identificare
Mappaggio di QTL – Per marcatori singoli o per intervalli (interval mapping)
!
ito
n
i
f
Produzione di granella in mais, reincrocio tra due linee inbred
de di mais (B73 x Mo17) x Mo17
n
No
Esempio
Un QTL è stato individuato
tra i marcatori C256 e C449,
vicino al locus
dell’isoenzima AMP3
In ordinata c'è Il
LOD score
In ascissa le distanze di
mappa (intervalli) in cM
Falconer e Mackay,
Introduction to
quantitative
genetics, 1996
Il LOD (Log of Odds) score misura la probabilità della posizione del QTL
E' infatti il logaritmo del rapporto tra due probabilità (Odds ratio):
L probabiltà dei dati osservati sotto l’ipotesi della presenza di un QTL in una
certa posizione di mappa
L0 probabilità dei dati osservati sotto l’ipotesi di assenza del QTL.
La posizione attribuita al QTL sulla mappa genetica è quella che rende massimo il valore
del LOD.
Il valore soglia di LOD per poter affermare di aver individuato un vero QTL è di solito pari
o superiore a 3, corrispondente a L:L0 > 1000:1
Si utilizzano software di mappaggio appositi (MapMaker-QTL, MapQTL, ecc.)
Il contributo di ciascun QTL alla varianza fenotipica della popolazione si
calcola sulla base dell'effetto medio della sostituzione allelica (v.
modello di Mather)
Infine, la varianza totale spiegata dall'insieme dei QTL si ottiene
sommando gli effetti di tutti i loci
2. Mappaggio “per associazione”, Association mapping o
Linkage disequilibrium (LD) mapping
Nella forma più avanzata si parla di
Genome Wide Association Studies (GWAS) e Selezione genomica
(Genomic selection, GS)
Per capire questi metodi bisogna avere le basi della
genetica delle popolazioni
Nota
Expression QTL (eQTL)
La tecnologia microarray (DNA chip) permette di misurare l'espressione di migliaia
di geni in un numero anche elevato di individui.
Il livello di espressione (trascrizione) dei geni di individui di una popolazione
segregante sono trattati come fenotipi di caratteri quantitativi. Essi possono
quindi essere mappati rispetto a marcatori molecolari.
In questo modo si individuano loci (eQTL) che influenzano il livello di espressione
di ciascun gene, che possono essere in cis e in trans.
Si tratta di esperimenti in tutto simili a quelli che individuano QTL, ma i fenotipi
sono costituiti dai livelli di trascrizione di molti geni, anche migliaia.
Narain P. Mol Breeding (2010) 26:135–143
Sommario
I caratteri più importanti economicamente sono quelli quantitativi
Per studiarli ci vuole la statistica...
I modelli statistici (modello multifattoriale) pur semplificando la realtà sono
di utilità pratica nel miglioramento genetico
Il mappaggio dei marcatori molecolari ci aiuta a dissezionare il controllo
genetico dei caratteri quantitativi e individuare QTL
La genetica delle popolazioni ci permetterà di capire l'effetto della selezione
e ci aiuta a isolare i geni (lezione seguente)