CORSO DI LAUREA IN SCIENZE BIOLOGICHE
Seconda prova in itinere di FISICA, 11 Giugno 2004
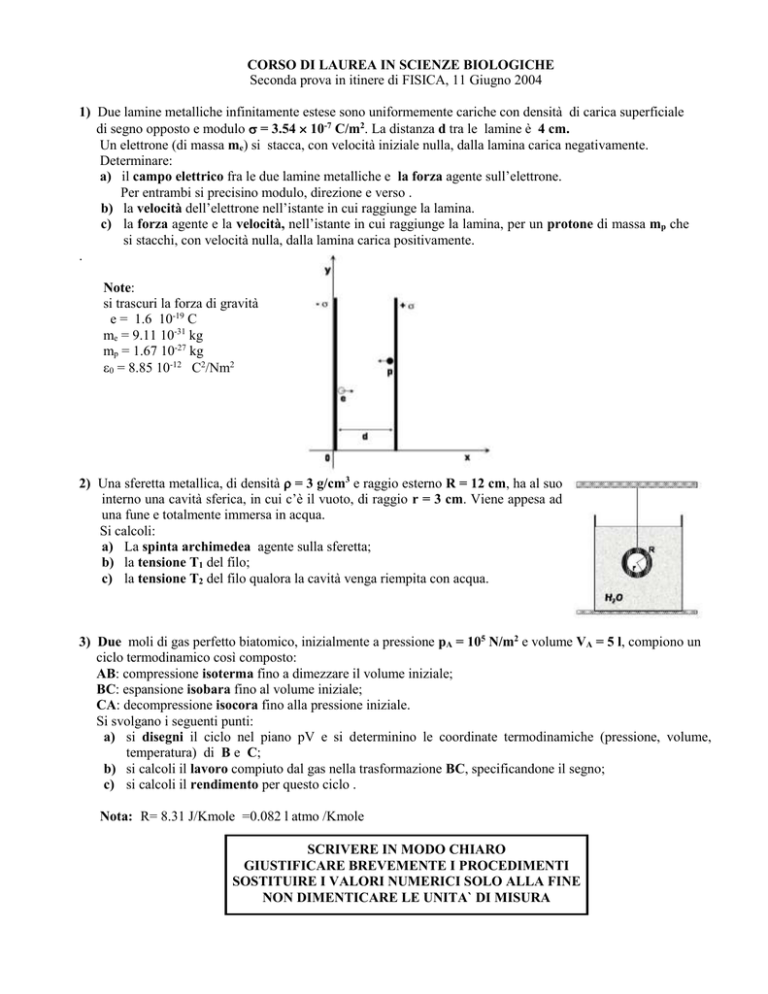
1) Due lamine metalliche infinitamente estese sono uniformemente cariche con densità di carica superficiale
di segno opposto e modulo = 3.54 10-7 C/m2. La distanza d tra le lamine è 4 cm.
Un elettrone (di massa me) si stacca, con velocità iniziale nulla, dalla lamina carica negativamente.
Determinare:
a) il campo elettrico fra le due lamine metalliche e la forza agente sull’elettrone.
Per entrambi si precisino modulo, direzione e verso .
b) la velocità dell’elettrone nell’istante in cui raggiunge la lamina.
c) la forza agente e la velocità, nell’istante in cui raggiunge la lamina, per un protone di massa mp che
si stacchi, con velocità nulla, dalla lamina carica positivamente.
.
Note:
si trascuri la forza di gravità
e = 1.6 10-19 C
me = 9.11 10-31 kg
mp = 1.67 10-27 kg
0 = 8.85 10-12 C2/Nm2
2) Una sferetta metallica, di densità = 3 g/cm3 e raggio esterno R = 12 cm, ha al suo
interno una cavità sferica, in cui c’è il vuoto, di raggio r = 3 cm. Viene appesa ad
una fune e totalmente immersa in acqua.
Si calcoli:
a) La spinta archimedea agente sulla sferetta;
b) la tensione T1 del filo;
c) la tensione T2 del filo qualora la cavità venga riempita con acqua.
3) Due moli di gas perfetto biatomico, inizialmente a pressione pA = 105 N/m2 e volume VA = 5 l, compiono un
ciclo termodinamico così composto:
AB: compressione isoterma fino a dimezzare il volume iniziale;
BC: espansione isobara fino al volume iniziale;
CA: decompressione isocora fino alla pressione iniziale.
Si svolgano i seguenti punti:
a) si disegni il ciclo nel piano pV e si determinino le coordinate termodinamiche (pressione, volume,
temperatura) di B e C;
b) si calcoli il lavoro compiuto dal gas nella trasformazione BC, specificandone il segno;
c) si calcoli il rendimento per questo ciclo .
Nota: R= 8.31 J/Kmole =0.082 l atmo /Kmole
SCRIVERE IN MODO CHIARO
GIUSTIFICARE BREVEMENTE I PROCEDIMENTI
SOSTITUIRE I VALORI NUMERICI SOLO ALLA FINE
NON DIMENTICARE LE UNITA` DI MISURA
SOLUZIONE ESERCIZIO 1
a) Le due piastre piane cariche producono al loro interno un campo
3.54 10 7 C / m 2
3
E i
i
(
40
10
N
/
C
)
i
0
8.85 10 12 C 2 / Nm 2
ossia perpendicolare alle due piastre e con verso dalla piastra positiva a quella negativa.
La forza elettrica subita dall’elettrone è pari a
3.54 10 7 C / m 2
Fe qE eE (e)( )i (1.6 10 19 C )
i (0.64 10 14 N ) i
12
2
2
0
8.85 10 C / Nm
ossia è diretta lungo x con verso concorde all’asse.
b) L’ accelerazione subita dall’elettrone è unicamente dovute alla forza elettrostatica, originata dal
campo elettrico:
Fe me ae eE
ossia:
eE (1.6 10 19 C )( 40 10 3 N / C )
ae
i (7.03 1015 m / s 2 )i
31
me
9.1 10 kg
Essendo l’accelerazione costante, il moto all’interno delle due piastre è rettilineo uniformemente
accelerato, per cui il legame fra velocità e posizione (quando l’elettrone urta l’armatura) è dato da:
v 2e v02e 2ae ( x f xi ) 0 2ae d 2ae d
v e 2ae d 2(7.03 1015 m / s 2 )(0.04m) 2.37 10 7 m / s
c) La forza elettrica che agisce sul protone è pari a
e
3.54 10 7 C / m 2
Fp qE eE
i (1.6 10 19 C )
i (0.64 10 14 N ) i
12
2
2
0
8.85 10 C / Nm
ossia la forza è uguale in modulo e direzione a quella agente sull’elettrone, ma con verso opposto.
Anche nel caso del protone, l’accelerazione subita è unicamente dovute alla forza elettrostatica,
originata dal campo elettrico:
Fp m p a p eE
(1.6 10 19 C )( 40 10 3 N / C )
eE
ap
i (3.83 1012 m / s 2 )i
27
mp
1.67 10 kg
ed il moto del protone è uniformemente accelerato lungo x, con verso opposto all’asse.
La velocità del protone all’istante in cui tocca la lamina è data da:
v 2p v02 p 2a p ( x f xi ) 0 2a p (0 d ) 2a p d
v p 2a p d 2(3.83 1012 m / s 2 )(0.04m) 5.5 10 5 m / s
SOLUZIONE ESERCIZIO 2
a) La spinta archimedea FA è pari al peso di fluido spostato (ossia acqua,di densità H2O = 103kg/m3):
4
4
FA m H 2O g H 2OVg H 2O ( R 3 ) g (10 3 kg / m 3 )( (0.12m) 3 )(9.8m / s 2 ) 70.9 N
3
3
b) All’equilibrio, la forza netta agente sulla sfera è nulla:
Fnet Fg FA T1 0
Proietto tale equazioni sull’asse y:
Fg FA T1 0
da cui si ricava la tensione T1:
T1 Fg FA
Dato che la forza peso Fg vale:
4
4
kg
Fg mg ( R 3 r 3 ) g ((0.12m) 3 (0.04m) 3 )(3 10 3 3 )(9.8m / s 2 ) 204.9 N
3
3
m
T1 Fg FA 204.9 N 70.9 N 134 N
c) Nel caso in cui la cavità venga riempita d’acqua, l’equilibrio delle forze dà:
Fnet Fg ( Fg ) H 2O FA T2 0
ove (Fg)H2O rappresenta la forza peso relativa alla cavità interna piena d’acqua. La spinta
idrostatica FA rimane uguale, dato che il volume di liquido spostato è il medesimo.
Proietto tale equazione lungo y:
Fg ( Fg ) H 2O FA T2 0
da cui ricavo la tensione T2:
T2 Fg ( Fg ) H 2O FA
Il peso della cavità piena d’acqua è pari a:
4
kg 4
( Fg ) H 2O H 2O r 3 g (3 10 3 3 ) (0.04m) 3 (9.8m / s 2 ) 7.9 N
3
m 3
Quindi:
T2 Fg ( Fg ) H 2O FA 204.9 N 7.9 N 70.9 N 141.9 N
SOLUZIONE ESERCIZIO 3
a) Per calcolare (p,V,T) nei punti B e C del ciclo applico
l’equazione di stato dei gas perfetti pV=nRT:
in B:
TB T A
p AV A (10 5 N / m 2 )(5 10 3 m 3 )
30 K
nR
2 moli 8.31 J / moleK
In una trasformazione isoterma pV = costante, quindi
p AV A p BVB p B
VA
2
p B 2 p A 2 10 N / m
5
da cui si ottiene:
2
VB = VA/2 = 2.5 litri = 2.5 10-3 m3
in C:
pB = pC = 2 105 N/m2
VC = VA = 5 litri = 5 10-3 m3
TC
pCVC (2 10 5 N / m 2 )(5 10 3 m 3 )
60 K
nR
2 moli 8.31 J / moleK
b) Il lavoro fatto dal gas in una trasformazione termodinamica è pari all’integrale sotteso dalla curva
nel piano pV. Nella trasformazione BC, a pressione costante, il lavoro è dato da:
C
V
LBC pdV p B (VC VB ) 2 p A (V A A ) p AV A 10 5 N / m 2 5 10 3 m 3 500 J
2
B
Il lavoro ha segno positivo, in quanto è fatto dal gas trattandosi di una espansione.
c) Il rendimento in un ciclo termodinamico è pari al rapporto fra il lavoro svolto ed il calore
assorbito. Nel ciclo in questione, il lavoro totale è dato
L LAB LBC poiché lungo CA (isocora) il lavoro è nullo.
Calcoliamo il lavoro lungo AB (isoterma), utilizzando la legge dei gas perfetti pV=nRTA:
B
L AB
B
V
V /2
dV
dV
pdV nRT A
nRT A
nRT A ln B nRT A ln A
V
V
VA
VA
A
A
A
nRT A ln
B
1
nRT A ln 2 p AV A ln 2 346.6 J
2
Il lavoro totale è quindi
L L AB LBC 346.6 J 500 J 153.4 J
Valuto ora gli scambi di calore lungo le 3 trasformazioni, applicando, il primo principio:
AB : Eint Q AB L AB 0 Q AB L AB 0
V
7
7
7
7
nR(TC TB ) ( pCVC p BVB ) 2 p A (V A A ) p AV A 1750 J 0
2
2
2
2
2
0 Eint Q ACA LCA QCA 0
BC : QBC nc p (TC TB )
CA : T diminuisce , LCA
Il rendimento del ciclo è quindi dato da: = L/QBC = 153.4 J/1750 J = 8.76 %












