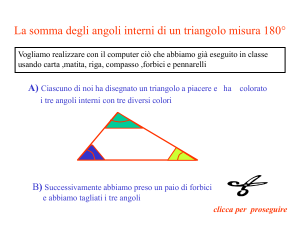
Una dimostrazione diversa dal solito
In matematica occorre "motivare". Non basta convincersi: occorre "convincere un
nemico", anche perché, in alcuni casi, si dimostra un fatto inaspettato, sorprendente.
Cominciamo con un esempio classico:
«In un qualunque triangolo, la somma degli angoli interni è un angolo piatto.»
Per convincerci che questo enunciato è corretto, possiamo misurare i tre angoli, con
un goniometro o con un software geometrico.
Primo problema: qualche volta, misurando con un software, la somma è 179°.
Oppure possiamo ripiegare un triangolo di carta.
Secondo problema: l'enunciato è vero per tutti i triangoli?
Differenza fra dimostrazione e verifica: basta una dimostrazione al posto di infinite
verifiche.
In figura è illustrata la dimostrazione usuale,
in cui si applica l’assioma delle parallele.
Un altro enunciato: «La somma degli angoli esterni
di un qualsiasi poligono P è uguale ad un angolo
giro (2 angoli piatti).»
Seguiamo il contorno del poligono con un
fiammifero: in ogni vertice V il fiammifero ruota di
un angolo uguale all'angolo esterno in V.
Il fiammifero fa un giro completo (2 piatti); la somma degli angoli esterni è ...
Nel caso di un triangolo,
angoli interni + angoli esterni = 3 piatti; quindi la somma degli angoli interni è ...
Consideriamo ora un "pentagono
intrecciato" come la stella in figura.
Qual è la somma degli angoli nelle 5
punte?