Corsi di Laurea in Ingegneria Biomedica, dell’Informazione, Elettronica e Informatica
Canale 3 (Prof. G. Naletto)
Prima Prova in Itinere di Fisica Generale 1 - Padova, 21 Aprile 2012
Cognome .............................................................. Nome ........................................... Matricola .......................
Problema 1
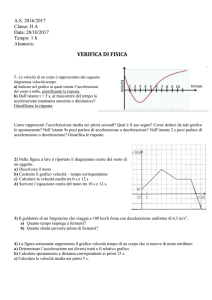
Due corpi puntiformi A e B possono muoversi su una guida circolare orizzontale priva di
attrito di raggio R = 1.2 m. I due corpi sono inizialmente fermi in due punti diametralmente
opposti. Un terzo corpo puntiforme C, non vincolato alla guida, è fermo su un punto della
guida stessa intermedio tra A e B. All’istante iniziale to = 0 A e B si mettono in moto nello
C
R
stesso verso, con B che si sposta verso C secondo la distanza minore sulla guida (verso
θ
antiorario in figura); i due corpi hanno accelerazioni angolari rispettivamente αA = 0.2 rad/s2 e
αB = 0.15 rad/s2; C rimane fermo. Determinare:
B
a) l’angolo θA complessivamente percorso da A dall’istante to a quando incontra B.
Nell’istante in cui, continuando il suo moto, il corpo A passa sopra la posizione occupata da B all’istante to, esso viene
lasciato uscire tangenzialmente dalla guida senza essere più soggetto ad alcuna accelerazione. Nello stesso istante in cui
A esce dalla guida, C viene messo in moto con accelerazione costante di modulo aC tangente alla guida. Determinare:
b) il modulo aA dell’accelerazione di A un istante prima di uscire dalla guida;
c) il modulo aC dell’accelerazione che deve avere il corpo C affinché A e C si incontrino in un punto.
A
Problema 2
Un corpo A di massa mA si trova su un piano scabro (coefficienti di attrito statico e
dinamico uguali e pari a µ = 0.15) inclinato di un angolo θ = 25° rispetto
A
all’orizzontale; esso è collegato verso l’alto ad una fune ideale inestensibile tesa
parallela al piano inclinato. Per mezzo del sistema di due carrucole ideali, una fissa e
θ
una mobile, mostrato in figura, l’altro estremo della fune è fissato verticalmente ad
B
un soffitto, ed un corpo B di massa mB = 3 kg è mantenuto sollevato dal suolo
collegato ad un’altra fune ideale verticale. Determinare:
a) il minimo valore mA,min della massa di A che mantiene il sistema in equilibrio statico.
Nell’ipotesi che la massa di A sia mA = mB/2, determinare:
b) il modulo aA dell’accelerazione di A;
c) il modulo R della reazione vincolare esercitata dal soffitto;
d) la variazione ∆Em dell’energia meccanica del sistema dall’inizio del moto a quando il corpo B si è abbassato di
h = 0.2 m.
Problema 3
Una rampa di massa M = 5 kg è costituita, partendo dal basso, da un
tratto inclinato liscio seguito da un tratto orizzontale scabro BC di
lunghezza l = 0.25 m e coefficiente di attrito dinamico µ = 0.05 e da
B
C
un altro tratto inclinato liscio. Inizialmente la rampa si muove di moto
V
o
m
rettilineo uniforme con velocità di modulo Vo = 0.8 m/s nel verso
M
A
indicato in figura su di un piano orizzontale liscio. Sul tratto inclinato
posto in basso, fermo nella posizione A, si trova un corpo di
dimensioni trascurabili e di massa m = M/5 che mantiene compressa una molla ideale di costante elastica k = 450 N/m
posta parallela al piano inclinato. Ad un certo istante il corpo viene sbloccato e la spinta della molla lo fa salire sulla
rampa. Si osserva che nell’istante in cui il corpo si trova sul punto B del tratto orizzontale la sua velocità, nel sistema di
riferimento fisso, ha modulo vB = 2Vo. Determinare:
a) il modulo VB della velocità della rampa nell’istante in cui il corpo di massa m si trova sul punto B;
b) la compressione iniziale ∆x della molla, sapendo che la differenza di quota verticale tra i punti A e B è hBA = 0.2 m;
c) la velocità vCM del centro di massa del sistema quando il corpo si ferma sul tratto scabro BC.
Soluzioni
Problema 1
1
1
α At 2 = π + α B t 2
2
2
a)
θ A (t ) = θ B (t ) ⇒
b)
2
ω A2 = ωoA
+ 2α A ∆θ = 2α A ⋅ 5π = 10πα A ;
⇒
t=
2π
αA −αB
⇒ θA =
αA
π = 4π rad
αA −αB
a A = aT2 , A + a N2 , A = (α A R)2 + (ω A2 R) 2 = (α A R)2 + (10πα A R) 2 = α A R 1 + 100π 2 = 7.54 m/s2
c)
A e C si incontrano quando entrambi hanno percorso la stessa distanza R.
aC
1
1
R = v A t* = ω A Rt * = Rt * 10πα A ⇒ t* =
; R = a C t *2 =
⇒ a C = 20πRα A = 15.1 m/s 2
2
20πα A
10πα A
Problema 2
a)
Si considera un asse parallelo al piano inclinato orientato verso l’alto.
T A − f as − m A g sin θ = 0
1
⇒ f as = g (mB − 2 m A sin θ ) ≤ f as ,max = µm A g cosθ
2
T
−
m
g
=
0
2
B
A
mB
⇒ mA ≥
= m A,min = 2.69 kg
2(sin θ + µ cosθ )
b)
c)
d)
⇒
T ' A − µm A g cosθ − m A g sin θ = m A a A
1
⇒ (mB − 2µm A cosθ − 2m A sin θ )g = 2m A a A + mB a A
aA
2
m
g
−
2
T
'
=
m
a
=
m
A
B B
B
B
2
(1 − µ cosθ − sin θ )g = 3 a A ⇒ a A = 2 g (1 − µ cosθ − sin θ ) = 2.88 m/s 2
2
3
1
R = T ' A = m A [a A + g (µ cosθ + sin θ )] = mB g (2 + µ cosθ + sin θ ) = 12.54 N
6
Considerando che un abbassamento di h di B corrisponde ad uno spostamento di 2h di A:
∆Em = Wattr = − µmA g ⋅ 2h cosθ = −µmB gh cosθ = −0.8 J
oppure
v2
1
1m
1
∆Em = m A v 2A + mB v B2 + m A g ⋅ 2h sin θ − mB gh = B v 2A + mB A + mB gh(sin θ − 1) =
2
2 2
4
2
1
3
= mB ⋅ (2a A ⋅ 2h ) + mB gh(sin θ − 1) = − µmB gh cosθ
2
4
⇒
Problema 3
La risultante delle forze esterne applicate al sistema è nulla, quindi si conserva la quantità di moto totale.
6
4
M
a)
2Vo + MVB ⇒ VB = Vo = 0.64 m/s
Pin = PB ⇒ ( m + M )Vo = mv B + MVB ⇒
MVo =
5
5
5
1
1
1
1
Em,TOT = costante ⇒
k∆x 2 + ( m + M )Vo2 = mv B2 + MVB2 + mghBA ⇒
b)
2
2
2
2
1
1
6
1
M
1
16
M
M 3
⇒
k∆x 2 = −
MVo2 +
4Vo2 + M Vo2 + ghBA = Vo2 + ghBA ⇒
2
25
2 5
2 25
5
5 5
2M 3 2
Vo + ghBA = 0.10 m
5k 5
Quando il corpo è fermo rispetto alla rampa, il sistema corpo+rampa si muove alla velocità Vo per la
conservazione della quantità di moto:
⇒ ∆x =
c)
v CM = Vo = 0.8 m/s