Liceo Scientifico “F. Lussana”
Programma svolto per la classe 1a E
disciplina: Fisica / docente: prof. Mora Paolo
Unità 1.
a s 2013 – 2014
La misura delle grandezze fisiche (unità 1 del libro di testo, lezioni 1.1 – 1.5)
1.1.
Grandezze fisiche, unità di misura, Sistema Internazionale delle unità di misura
1.2.
Operazioni tra grandezze fisiche. Misure dirette e indirette
1.3.
La notazione scientifica. Ordini di grandezza. Cifre significative
1.4.
La misura delle lunghezze. Multipli e sottomultipli
1.5.
Misure di aree, volumi
1.6.
La misura della massa
1.7.
La densità di una sostanza
Attività sperimentali e di laboratorio:
-
Misure di lunghezze con il righello e con il calibro.
Unità 2.
Le incertezze di misura (unità 1 del libro di testo, lezioni 1.5 – 1.6)
2.1. Errori di misura: errori accidentali ed errori sistematici
2.2. Incertezza associata a una misura diretta. Incertezza relativa e percentuale
2.3. Precisione ed affidabilità di una misura
2.4. Confronto tra due misure
2.5. Incertezza associata ad una misura indiretta
2.6. Cifre significative
2.7. Propagazione degli errori
2.8. Misure singole; misure ripetute
Attività sperimentali e di laboratorio:
-
Misura del tempo di oscillazione di un pendolo.
Misura del volume di un solido: confronto tra diversi metodi di misura.
Misure di densità dei solidi.
Unità 3.
Le relazioni tra le grandezze fisiche (unità 2 del libro di testo)
3.1. La rappresentazione di un fenomeno fisico mediante tabelle, formule, grafici
(interpolazione – estrapolazione)
3.2. La costruzione e l'interpretazione di un grafico cartesiano; incertezze nei grafici
3.3. Analisi di alcuni tipi di relazioni tra grandezze fisiche, dal punto di vista grafico e dal punto
di vista algebrico: la relazione di proporzionalità diretta, di proporzionalità inversa, di
proporzionalità quadratica; la correlazione lineare, la relazione inversa quadratica
3.4. Le proprietà algebriche delle relazioni tra le grandezze fisiche
3.5. Relazioni lineari e relativo studio mediante Excel e Geogebra
__________________________________________________________________________________
Programma svolto / Fisica / classe 1 E / a.s. 2013 – 2014 / pag. 1 di 2
Attività sperimentali e di laboratorio:
-
-
misure di distanze e dei tempi impiegati per percorrere tali distanze: il caso di una bolla d'aria
all'interno di un tubo di vetro contenente acqua e il caso di una biglia metallica in moto lungo un piano
inclinato;
misure di periodo di un pendolo al variare della lunghezza del filo; legge di Boyle (con l’ausilio del
labtech, acquisizione dati attraverso sonde collegate a p.c.)
uso del foglio elettronico e di GeoGebra per l'elaborazione dei dati sperimentali e per la costruzione dei
grafici; individuazione di una linea di tendenza; interpretazione dei grafici cartesiani; riconoscimento
della relazione di proporzionalità diretta e della relazione lineare.
-
Unità 4.
la temperatura, il calore e l'equilibrio termico
(Parte E del libro di testo, unità 11)
4.1. Dalla sensazione del caldo e del freddo alla misura della temperatura
4.2. Termometri e scale termometriche
4.3. La dilatazione termica
4.4. Legge fondamentale della termologia: calore specifico e capacità termica; equilibrio
termico
4.5. Cambiamenti di stato: punti fissi e loro variazione con la pressione; calore latente
4.6. Propagazione del calore per conduzione, convezione, irraggiamento; conducibilità termica
(legge di Fourier)
Attività sperimentali e di laboratorio:
-
dilatazione lineare di alcune aste metalliche; misura del coefficiente di dilatazione
-
Il testo adottato è: “Fisica – Lezioni e problemi – AB + EF”; Giuseppe Ruffo; edizione
Zanichelli;
Bergamo, il 05/06/2014
I rappresentanti degli studenti
__________________________
__________________________
Il docente
__________________________
(prof. Mora Paolo)
__________________________________________________________________________________
Programma svolto / Fisica / classe 1 E / a.s. 2013 – 2014 / pag. 2 di 2
Lavoro estivo di fisica / classe 1 E / a.s. 2013 – 2014
Esercizio 1. La velocità dell’acqua, all’interno di un acquifero sotterraneo, è di circa 1 metro al
giorno. Calcola, in secondi, il tempo impiegato da una goccia d’acqua per percorrere una
distanza di 100 Km . Esprimi il risultato utilizzando la notazione scientifica. Qual è l’ordine di
grandezza della misura trovata?
Esercizio 2. Calcola quante molecole sono contenute in 1 cm 3 di aria, sapendo che 22 litri di
aria, in condizioni standard di pressione e temperatura, contengono 6 10 23 molecole.
Esercizio 3. (*) Un blocco di massa 5 Kg è costituito da un materiale di densità 2 , 4 Kg dm 3 .
Se si aggiungono al blocco 0 , 8 Kg dello stesso materiale, di quanto aumenta il volume del
blocco ?
Esercizio 4. (*) Un battiloro prende 57 , 9 g di oro (densità 19 , 3 g cm 3 ) e lo martella fino ad
ottenere una lamina sottile, di forma quadrata, di lato 1 dm . Calcola lo spessore della lamina in
millimetri, esprimendo la misura in notazione scientifica.
Esercizio 5. Le ali di un insetto vibrano 173 volte in 7 secondi. Quanto dura un battito di ali?
(esprimi la misura in secondi, in notazione scientifica). Quanti battiti di ali vengono compiuti in
5 minuti ?
Esercizio 6. Completa le seguenti equivalenze, esprimendo il risultato in notazione scientifica:
32000 mm 2
0 , 0096 m 3
2 anni
7 , 83 g cm
1550 10 3 g
3
m2
litri
s
Kg m 3
Kg
Esercizio 7. Nella figura qui accanto è riprodotto
l’ingrandimento di un calibro ventesimale. A) Riporta
la misura indicata dallo strumento, spiegando in
dettaglio dove leggi i mm e dove leggi i decimi e i
centesimi di mm ; B) disegna la configurazione di un
calibro (parte fissa + parte mobile) in corrispondenza
della misura 35, 40 mm , utilizzando le seguenti
scale: la distanza tra due tacchette consecutive sulla
parte fissa vale 5 mm ; la distanza tra due tacchette
consecutive sulla parte mobile vale 4, 75 mm .
Esercizio 8. Completa le seguenti equivalenze, esprimendo il risultato in notazione scientifica:
3500 mm 2
0 , 96 m 3
m2
litri
_____________________________________________________________________
Lavoro estivo di fisica / classe 1 E / a.s. 2013 – 2014 / pag. 1 di 8
27 , 3 giorni
13 , 56 g cm
67 , 50 10 5 g
3
s
Kg m 3
Kg
Esercizio 9. In riferimento all’esperienza di misurazione del periodo di oscillazione di un pendolo:
A) esegui un disegno dell’apparecchiatura utilizzata; B) descrivi gli strumenti di misura
impiegati (specifica in particolare la portata e la sensibilità); C) illustra la procedura seguita per
le misurazioni; D) spiega (riportando i valori) come hai organizzato la raccolta dei dati (tabelle,
grafici, altro….) e come hai stimato gli errori delle grandezze fisiche misurate; E) illustra
l’elaborazione dei dati eseguita con foglio di calcolo e le conclusioni finali relative
all’esperienza.
Esercizio 10. (*) In riferimento all’esperienza di misurazione del volume di un solido con diversi
metodi: A) illustra i due metodi utilizzati, evidenziando i criteri scelti per associare l’errore
assoluto a ciascuna delle due misure; B) la sensibilità della bilancia 0 , 1 g è stata determinante
per la valutazione degli errori (motiva la tua risposta) ? C) quale delle due misure è risultata più
precisa ? perché ?
Esercizio 11. Cosa sono le cifre significative di una misura ? Come ci si comporta in riferimento
alle cifre significative quando si moltiplicano due misure ? e quando si sommano ?
Esercizio 12. [ propagazione degli errori ] Spiega come si valutano gli errori quando si sommano, si
sottraggono, si moltiplicano o si dividono tra loro due misure di cui si conoscono le incertezze
assolute.
Esercizio 13. In un esperimento analogo a quello effettuato in laboratorio, si è misurato il volume di
un solido mediante spostamento di liquido, valutando il peso dell’acqua spostata utilizzando una
bilancia di sensibilità 0 , 1 g . Ripetendo 5 volte la misura si sono ottenuti i seguenti valori:
107 , 2 g ; 109 , 3 g ; 108, 4 g ; 106 , 9 g ; 107 , 5 g
A) valuta, in cm 3 , la misura probabile del volume dell’oggetto ;
B) associa alla misura precedente un errore assoluto (spiega il criterio che utilizzi) ;
C) sapendo che l’oggetto è di alluminio (densità 2,75 0, 05 g cm 3 ), calcola la massa
probabile dell’oggetto ;
D) associa alla massa calcolata un errore assoluto (spiega il criterio che utilizzi).
Esercizio 14. [ propagazione degli errori ] Siano a a e b b misure di lunghezze con i
ab
una grandezza fisica derivata dalle due
a b
precedenti. Esprimi, in funzione di a ,b , a , b ,
corrispondenti errori assoluti. Sia G 2
l’errore assoluto G
e l’errore relativo r G
associati alla grandezza G .
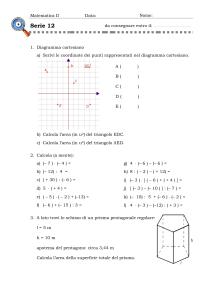
Esercizio 15. Nella figura sono indicate le misure dei lati
di un trapezio con i rispettivi errori; calcola area e
_____________________________________________________________________
Lavoro estivo di fisica / classe 1 E / a.s. 2013 – 2014 / pag. 2 di 8
perimetro del trapezio, con indicazione degli errori assoluti, relativi e percentuali.
Esercizio 16. Per misurare il volume di un corpo lo si pesa su una bilancia con sensibilità 0 , 01 g ,
ottenendo la misura 327 ,67 g . Sapendo che l’oggetto è di alluminio (densità
2,72 0 , 01 g , calcola il volume riportando correttamente l’errore assoluto (arrotondato ad
una cifra significativa), l’errore relativo e l’errore percentuale.
Esercizio 17. Con un calibro decimale, simile a quello utilizzato in laboratorio, si misurano le
dimensioni di una moneta ottenendo i seguenti risultati: spessore 1, 4 mm ;
diametro 25 , 5 mm . Esprimi il volume in cm 3 , riportando correttamente l’errore assoluto
(arrotondato ad una cifra significativa), l’errore relativo e l’errore percentuale.
Esercizio 18. Disponi in ordine, dalla più precisa alla meno precisa, le seguenti misure, riportando
tutti i calcoli necessari:
a)
18 cm3 volume di un bullone, misurato immergendolo in un cilindro graduato con sensibilità 1 ml;
b)
capacità di una bottiglia di plastica da 1,5 litri (incertezza di misura = 10 cm3);
c)
d)
massa di una mela, misurata con una bilancia di precisione = ( 120,0 ± 0,1 ) g;
0,8 mm spessore di un filo metallico, misurato con un calibro ventesimale (sensibilità 50
m).
Esercizio 19. (*) In riferimento all’esperienza relativa al moto di una biglia lungo un piano
inclinato: A) esegui un disegno dell’apparecchiatura utilizzata; B) descrivi gli strumenti di
misura impiegati (specifica in particolare la portata e la sensibilità); C) illustra la procedura
seguita per le misurazioni; D) spiega (riportando i valori !) come hai organizzato la raccolta dei
dati (tabelle, grafici, altro….) e come hai stimato gli errori delle grandezze fisiche misurate; E)
illustra l’elaborazione dei dati eseguita con foglio di calcolo e le conclusioni finali relative
all’esperienza (in particolare discuti il tipo di relazione che lega le grandezze L lunghezza e
T tempo).
Esercizio 20. Fornisci la definizione di pendenza di una linea retta rispetto ad un sistema cartesiano.
Esercizio 21. Illustra brevemente le caratteristiche algebriche e grafiche della proporzionalità
quadratica e della proporzionalità inversa. Per ciascuna di esse riporta un esempio fisico
significativo (spiega bene quali sono le due grandezze in gioco).
Esercizio 22. In un’esperienza analoga a quella effettuata in laboratorio, vengono agganciati dei
pesi ad una molla, provocandone diversi allungamenti. I dati raccolti sono riassunti nella
seguente tabella:
Peso (g) Lunghezza (cm)
32,00
11,00
47,00
15,00
66,00
18,00
89,00
21,00
124,00
29,00
_____________________________________________________________________
Lavoro estivo di fisica / classe 1 E / a.s. 2013 – 2014 / pag. 3 di 8
metri
1. Su un foglio di carta millimetrata riporta i dati in un grafico cartesiano (peso in ascisse,
cioè in orizzontale), utilizzando le seguenti scale: in orizzontale P 10 g 1cm ; in
verticale L 3 cm 1 cm ;
2. traccia, sul riferimento cartesiano precedente, la retta che meglio si avvicina ai 5 punti
del grafico, fino ad intersecare l’asse delle lunghezze in un punto A ;
3. dal grafico deduci la lunghezza della molla a riposo ;
4. dal grafico (interpolazione) deduci quale sarebbe la lunghezza della molla agganciando
ad essa un peso di 100 g ;
5. stima la pendenza della retta disegnata (attenzione alle unità di misura) e spiegane il
significato fisico.
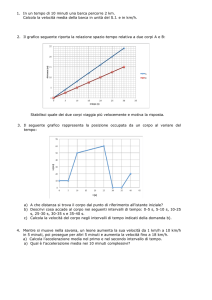
Esercizio 23. Determina per via grafica, con la
maggior precisione possibile, i valori delle
pendenze delle rette qui a fianco riportate, con le
corrette unità di misura. Quale fenomeno, tra
quelli osservati in laboratorio, potrebbe essere
descritto da grafici di questo tipo ? (motiva
accuratamente la tua risposta).
secondi
Esercizio 24. L’elasticità di una molla ideale è
cm
descritta dalla misura 0 , 45
. La molla ha una
g
lunghezza a riposo di 7 , 6 cm . Si indichi con L
la lunghezza che la molla assume quando viene
agganciato ad essa un peso P .
1. calcola quanti grammi è necessario agganciare per ottenere un allungamento di 1cm ;
2. scrivi l’equazione che esprime la variabile L in funzione del peso P ;
3. scrivi l’equazione che esprime la variabile P in funzione della lunghezza L ;
Esercizio 25. (*) In riferimento all’esperienza relativa alla legge di Boyle (relazione tra volume
occupato dall’aria in una siringa e corrispondente pressione): A) esegui un disegno
dell’apparecchiatura utilizzata; B) illustra la procedura seguita per le misurazioni, descrivendo in
modo sufficientemente accurato le operazioni eseguite col p.c.; C) spiega (riportando i valori !)
come hai organizzato la raccolta dei dati (tabelle, grafici, altro….); D) illustra l’elaborazione dei
dati eseguita con foglio di calcolo e le conclusioni finali relative all’esperienza.
Esercizio 26. (*) In un’esperienza analoga a quella effettuata in laboratorio, viene studiata la
relazione tra il volume occupato da una certa quantità di aria e la pressione esercitata. I dati
raccolti sono riassunti nella seguente tabella:
Volume (cc)
32
37
51
72
84
104
Pressione (KPa)
65
53
39
28
24
19
1. Riporta i dati in un grafico cartesiano (Volume in ascisse, cioè in orizzontale),
utilizzando opportune scale che provvederai ad esplicitare;
2. Disegna una linea (curva !) che interpoli i punti assegnati; che tipo di curva si ottiene ? ;
_____________________________________________________________________
Lavoro estivo di fisica / classe 1 E / a.s. 2013 – 2014 / pag. 4 di 8
3. Dal grafico (interpolazione) deduci quale sarebbe la pressione in corrispondenza di un
volume di 60 cc ;
4. Prova ad ipotizzare una possibile equazione che leghi le variabili P e V ; utilizza tale
relazione per determinare il volume corrispondente ad una pressione di 101 KPa (cioè
la pressione atmosferica).
Esercizio 27. Su una bolletta del gas metano sono indicati 60 euro al mese di costi fissi per la
fornitura del gas più un costo di 0,7 euro per ogni metro cubo di metano consumato. Sapendo
che la spesa nel mese di gennaio è stata di 200 euro, calcola quanti metri cubi di metano sono
stati consumati nel mese di gennaio.
Esercizio 28. Quando a una molla è appeso un oggetto di massa 10 g, la lunghezza della molla è 10
cm, mentre quando è appeso un oggetto di massa 30 g, la lunghezza diventa 20 cm.
Riporta in valori della massa appesa alla molla e della lunghezza della molla in un grafico cartesiano (massa
sull’asse X, lunghezza sull’asse Y). Che tipo di relazione c’è tra la massa appesa e la lunghezza della molla? Sei in
grado di ricavare l’equazione che descrive tale relazione ? Se la lunghezza della molla, quando è appeso un anello
d'oro, è 14 cm, qual è la massa dell'anello ? (risolvi sia graficamente che analiticamente, confronta poi i risultati
ottenuti).
Esercizio 29. Un’automobilista vuole percorrere un tratto di autostrada lungo 60 km e vuole
calcolare il tempo impiegato a percorrere questa distanza in funzione della velocità media di
percorrenza.
Determina il tempo di percorrenza, ed esprimilo in minuti, nei seguenti casi:
a. velocità media di percorrenza = 90 km/h;
b. velocità media di percorrenza = 120 km/h;
c. velocità media di percorrenza = 150 km/h.
Riporta in valori della velocità e del tempo di percorrenza in un grafico cartesiano (velocità sull’asse Y, tempo
sull’asse X). Che tipo di relazione c’è tra la velocità e il tempo di percorrenza? Esprimi anche la relazione
analitica tra le variabili V = velocità e T = tempo).
Esercizio 30. (*) Un disco di diametro 10 cm e spessore 2 mm ha una massa di 42,4 g. Calcola la
densità del materiale con cui è stato costruito il disco. Con lo stesso materiale si costruisce un
disco di uguale spessore, ma avente un diametro di 20 cm. Quale sarà, in tal caso, il valore della
massa del disco ? Immagina ora di costruire, sempre col medesimo materiale, tanti dischi di
uguale spessore, con diametri diversi. Quale tipo di relazione sussiste tra M = massa del disco e
D = diametro del disco stesso ?
Esercizio 31. In un laboratorio sono presenti quattro cilindri di diverso materiale (piombo, rame,
ferro e alluminio), aventi tutti una massa di 100 g e un’altezza di 4 cm. Utilizzando i valori di
densità riportati in tabella, calcola il diametro dei quattro cilindretti.
MATERIALE
PIOMBO
RAME
FERRO
ALLUMINIO
DENSITA’ ( kg / m3 )
11400
8900
7800
2700
Riporta i valori del diametro e della densità dei quattro oggetti in un grafico cartesiano (diametro sull’asse X,
densità sull’asse Y). Che tipo di relazione c’è tra il diametro e la densità ?
Esercizio 32. (*) La massa di un metro cubo di aria vale 1,3 kg. Sapendo che l’aria è costituita
essenzialmente da una miscela di azoto e ossigeno, che 1 metro cubo di azoto ha una massa di
1,26 kg mentre 1 metro cubo di ossigeno ha una massa di 1,46 kg, determina le percentuali in
volume di azoto e di ossigeno che compongono l’aria; determina poi le percentuali in massa di
azoto e di ossigeno che compongono l’aria.
_____________________________________________________________________
Lavoro estivo di fisica / classe 1 E / a.s. 2013 – 2014 / pag. 5 di 8
Esercizio 33. (*) La bolletta del telefono prevede 20 euro al mese di costi fissi (linea, abbonamento
ecc.) + 0,03 euro / minuto per ogni telefonata. Sapendo che la spesa media mensile è di 50 euro,
calcola la durata complessiva delle telefonate.
Esercizio 34. Un gioiello, composto in parte d'oro e in parte d'argento, ha una massa di 100 g e
occupa un volume di 8 cm3. Sapendo che la densità dell'oro è 19,3 g/cm3 mentre la densità
dell'argento è 10,5 g/cm3 , calcola la percentuale di oro (sia in volume che in massa) contenuta
nel gioiello.
Esercizio 35. (*) Un recipiente di alluminio di forma cilindrica, avente una capacità di 800 ml, viene
usato come contenitore per vernici. Sapendo che il diametro di base del recipiente vale 5 cm,
determina l’altezza del recipiente e l’area della superficie totale. La ditta che produce i
contenitori sta valutando l’opportunità di modificare le dimensioni del recipiente, mantenendo
costante la capacità di 800 ml e facendo in modo che la forma rimanga sempre cilindrica, in
modo da utilizzare una quantità minore di alluminio per la fabbricazione dei recipienti. Si valuta
pertanto se modificare il diametro e l’altezza del recipiente e si considerano a questo proposito
tre valori possibili per il diametro: 5 cm, 10 cm, 20 cm. In quale di questi tre casi, l’area della
superficie del recipiente risulta minore?
Esercizio 36. Una sfera di diametro d1 = 3 cm ha una massa m1 = 110 g. Calcola la densità del
materiale con cui è stato costruita la sfera. Con lo stesso materiale si costruisce una sfera avente
un diametro d2 = 6 cm. Quale sarà, in tal caso, il valore della massa m2 della sfera? Quale tipo di
relazione sussiste tra la massa della sfera e il diametro?
Esercizio 37. (*) In figura è riportata una parte della strumentazione utilizzata
nell’esperienza relativa alla dilatazione lineare di una bacchetta di
rame/ferro/vetro.
Spiega l’utilizzo di quest’asta metallica in relazione all’obiettivo
dell’esperimento
Illustra il ragionamento di tipo geometrico che lega le variabili L ed s
di figura con lo spostamento x letto sulla punta dell’asta e con
l’allungamento l della bacchetta.
In un esperimento di laboratorio, in relazione alla dilatazione termica
di un bacchetta metallica di lunghezza 50 cm , si ottengono le seguenti
misure: L 12 cm ; s 2 m m ; variazione di temperatura
L
t 80 oC 1 ; x 4, 8cm . Calcola l’allungamento l della
bacchetta e il coefficiente di dilatazione lineare del metallo di cui è
costituita la bacchetta.
Esercizio 38. In una vasca da bagno vuoi miscelare acqua a 49 , 0 oC con acqua a 13 , 0 oC per
portare la massa complessiva dell’acqua ad una temperatura di equilibrio di 36 , 0 oC . La massa
totale dell’acqua è 191 Kg . Trascurando la dispersione di calore tra l’acqua e l’ambiente, quanti
Kg di acqua calda e quanti di acqua fredda devi miscelare? [ calore specifico dell’acqua
J
4186
]
K g o C
Esercizio 39. Fornisci le definizioni di: massa equivalente (in acqua) di un calorimetro; potenza di
un fornello.
_____________________________________________________________________
Lavoro estivo di fisica / classe 1 E / a.s. 2013 – 2014 / pag. 6 di 8
Esercizio 40. Dopo aver fornito la definizione (precisa !) di calore specifico di una data sostanza,
risolvi il problema di seguito proposto.
Per una buona frittura la temperatura dell’olio deve essere almeno di 160 gradi. Una friggitrice
ha una potenza di 1,0 KWatt e contiene 2,5 litri di olio di oliva (densità 0, 92 g cm 3 ), che
inizialmente è alla temperatura di 20 gradi. Trascurando le dispersioni di calore calcola il tempo
che si deve attendere dall’accensione della friggitrice prima di immergere nell’olio le patatine. [
calore specifico dell’olio 1650 J K g o C ].
Esercizio 41. Fornisci la definizione di calore latente di fusione per una sostanza allo stato solido.
Quindi risolvi il problema proposto.
Un orafo vuole fondere un lingotto di 200 grammi di oro che si trova inizialmente ad una
temperatura di 20 gradi; utilizza a tale scopo un forno che ha una potenza di 600 Watt.
La temperatura di fusione dell’oro è di 1064 gradi, il calore latente di fusione dell’oro vale
6, 3 104 J K g , il calore specifico dell’oro solido vale 130 J K g o C .
3.1.
Calcola la quantità di calore necessaria per scaldare e fondere il lingotto;
3.2.
supponendo che la dispersione termica si possa stimare nel 25% dell’energia erogata
dal forno, calcola il tempo impiegato per riscaldare il lingotto da 20 a 1064 gradi e il
tempo necessario per fondere il lingotto;
3.3.
rappresenta il fenomeno studiato in un grafico temperatura – tempo [temperatura in
gradi sull’asse delle ordinate; tempo in secondi sull’asse delle ascisse].
Esercizio 42. (*) Si mette un cubetto di ghiaccio di 0 , 072 Kg , alla temperatura di 0 , 0 oC , in una
tazza di polistirolo espanso (perfettamente isolante) contenente 0 , 35 Kg di acqua alla
temperatura di 15 , 0 oC . Ipotizzando che il sistema cubetto acqua sia perfettamente isolato
dall’ambiente esterno, spiega (svolgendo opportuni calcoli) perché il cubetto non si scioglie
completamente e calcola la massa di ghiaccio residua quando l’acqua raggiunge la temperatura
di 0 , 0 oC . [il calore latente di fusione del ghiaccio vale 33 , 5 10 4 J Kg , il calore specifico
dell’acqua vale (ovviamente !) 1 cal g oC , ricorda che: 1 cal 4 , 186 J ].
Esercizio 43. Il calore specifico di un certo metallo viene determinato misurando la variazione di
temperatura che si produce quando si pone un pezzo riscaldato del metallo in un recipiente
isolato fatto dello stesso materiale e contenente acqua. Il pezzo di metallo ha una massa di
100 g ed è inizialmente a 100 oC ; il recipiente ha una massa di 200 g e contiene 500 g di
acqua alla temperatura iniziale di 17 , 3 oC . La temperatura finale del sistema è 22,7 oC . Qual è
il calore specifico del metallo?
Esercizio 44. (*) Due cubi metallici, uno di piombo (Pb) e l’altro di argento (Ag),
aventi lo spigolo di 2 cm , sono disposti com’è mostrato in figura. Sapendo
che i coefficienti di conducibilità termica del Pb e dell’Ag valgono
_____________________________________________________________________
Lavoro estivo di fisica / classe 1 E / a.s. 2013 – 2014 / pag. 7 di 8
rispettivamente 353
W
m oC
e 429
W
, indicata con T la temperatura all’interfaccia (
m oC
giunzione Pb – Ag):
i.
esprimere, in funzione di T , la quantità di calore che nell’unità di tempo attraversa il Pb
(utilizzando il Watt come unità di misura)
ii.
esprimere, in funzione di T , la quantità di calore che nell’unità di tempo attraversa l’Ag
(utilizzando il Watt come unità di misura)
iii.
calcolare, uguagliando le due grandezze precedentemente trovate, la temperatura T
iv.
determinare le temperature nei centri dei due cubi (giustificare accuratamente le
relazioni utilizzate !)
Esercizio 45. Un’automobile ha il serbatoio d’acciaio di 60 l , riempito fino all’orlo con benzina,
alla temperatura di 10 oC . Il coefficiente di dilatazione volumica della benzina è
0 , 900 10 3 oC 1 ; il coefficiente di dilatazione lineare dell’acciaio vale 11 10 6 oC 1 . Calcola
quanta benzina trabocca se l’automobile è parcheggiata al sole e la sua temperatura aumenta fino
a 25 oC .
Esercizio 46. Per una buona frittura la temperatura dell’olio deve essere almeno di 160 gradi. Una
friggitrice ha una potenza di 1,0 KWatt e contiene 2,5 litri di olio di oliva (densità
0, 92 g cm 3 ), che inizialmente è alla temperatura di 20 gradi. Trascurando le dispersioni di
calore calcola il tempo che si deve attendere dall’accensione della friggitrice prima di immergere
nell’olio le patatine. [ calore specifico dell’olio 1650 J Kg oC ].
Esercizio 47. Mediante un’esperienza di laboratorio si vuole determinare il calore specifico di un
oggetto solido metallico misurando la variazione di temperatura che si produce quando si pone
l’oggetto in un calorimetro contenente acqua. Il pezzo di metallo ha una massa di 300 g ed è
o
o
inizialmente a 100 C ; il recipiente contiene 250g di acqua alla temperatura iniziale di 20, 9 C .
o
La temperatura finale del sistema è 33, 6 C . Qual è il calore specifico del metallo?
Suggerimento per letture estive:
“Più o meno quanto ?” // Weinstein, Adam // Zanichelli Editore // 2009 // € 11,80 (circa)
L’arte di fare stime sul mondo
Istruzioni per l’uso: gli studenti che hanno giudizio sospeso in fisica sono tenuti a
svolgere tutti gli esercizi (tale lavoro sarà controllato a settembre 2014,
contestualmente alla prova orale); gli altri studenti sono tenuti a svolgerne almeno la
metà, includendo nella scelta tutti gli esercizi contrassegnati dal simbolo (*) [ ad es. :
Esercizio 44 (*) ].
auguro a voi e alle vostre famiglie una serena estate,
_____________________________________________________________________
Lavoro estivo di fisica / classe 1 E / a.s. 2013 – 2014 / pag. 8 di 8