1 L`Oscillatore armonico 2 Oscillatore armonico libero

1
L’Oscillatore armonico
L’oscillatore armonico è un interessante modello fisico che permette lo studio di fondamentali grandezze meccaniche sia da un punto di vista teorico
che sperimentale. Le condizioni di validità del modello sono facilmente realizzabili sperimentalmente e le leggi a cui è soggetto si prestano a semplici
verifiche di laboratorio. Innumerevoli sono i sistemi fisici (macroscopici e
microscopici) la cui dinamica segue le leggi dell’oscillatore armonico. Una
massa sospesa ad una molla o ad un filo nel campo di gravità permette lo
studio di due semplici esempi di sistemi oscillanti. Il pendolo semplice in
regime di piccole oscillazioni viene descritto dall’equazione dell’oscillatore
armonico valida per forze di tipo elastico (legge di Hooke). Il pendolo composto poi è un conveniente sistema che permette di passare dalla meccanica
del punto materiale a quella dei corpi rigidi. Si possono utilizzare per lo studio delle piccole oscillazioni del sistema due modelli di pendoli reversibili; il
primo a coltelli variabili e massa fissa ed il secondo a coltelli fissi e masse
mobili (i pendoli di Kater). La descrizione dei due sistemi è la stessa e richiede l’introduzione delle grandezze meccaniche quali il momento di inerzia, il
momento della quantità di moto e il centro di massa. La determinazione
sperimentale di g viene però ricondotta alla misura di solo due grandezze
equivalenti alla lunghezza e al periodo di un pendolo semplice.
2
Oscillatore armonico libero
Consideriamo una forza di tipo elastico che segue la legge di Hooke:
Fx = −kx,
(1)
dove x è la coordinata dell’estremo della molla.
Le molle metalliche elicoidali sollecitate lungo l’asse delle spire producono
forze di richiamo ben descritte dalla precedente espressione per ampi valori
delle deformazioni: anche alcune volte la lunghezza della molla a riposo.
L’oscillatore armonico ideale è costituito da una massa non pesante (non
soggetta a forza di gravità) soggetta ad una forza di tipo elastico Eq. (1).
L’equazione del moto del sistema è:
mẍ = −kx;
ẍ +
k
x = 0;
m
ẍ + ω02 x = 0,
(2)
dove si è introdotta la pulsazione angolare:
s
ω0 =
k
m
costante con le dimensioni dell’inverso di un tempo.
1
(3)
Figura 1: Molla con massa appesa
La soluzione della Eq. (2) è della forma:
x(t) = X sin(ω0 t + φ),
(4)
dove X e φ sono l’ampiezza e la fase costanti. Si può verificare la validità
della Eq. (4) mediante le due derivate:
ẍ = −ω02 X sin(ω0 t + φ),
ẋ = ω0 X cos(ω0 t + φ);
(5)
per cui:
ẍ + ω02 x = 0.
3
(6)
Massa sospesa ad una molla
Un sistema comodo e semplice per lo studio sperimentale dell’oscillatore
armonico è costituito da una massa sospesa ad una molla nel campo di gravità. All’equilibrio l’elongazione della molla bilancerà la forza peso dovuta
sia alla massa esterna m che alla massa stessa della molla mm . Misurando
per alcune masse mi le corrispondenti elongazioni xi si può determinare la
costante k della molla e la massa stessa mm .
Le due costanti k ed mm possono essere determinate ulteriormente in
regime dinamico misurando il periodo di oscillazione in funzione della massa
sospesa. La relazione di facile verifica sperimentale è:
4π 2
m,
(7)
k
valida rigorosamente in assenza di attriti. In effetti il regime di un oscillatore
reale è di tipo smorzato per cui la relazione precedente è solo un’approssimazione che risulta ragionevole nel limite di piccoli smorzamenti. Rimandiamo
al paragrafo (8) lo studio dell’oscillatore smorzato.
T02 =
2
Z 6
O
A
A
A
θA
A
A
A
A
A L
@
A
@
A
@
A
@
A
@
A
@ A
@ A P
@A
@}
@
@
@
@
@
@
@
@
@
@
? mg
@
@
@
X @
R Y
@
Figura 2: Pendolo semplice
4
Il pendolo semplice
Il pendolo semplice è costituito da una massa pesante puntiforme m vincolata, mediante un filo inestensibile privo di massa, a ruotare attorno ad un
punto fisso O in un piano verticale (Fig. 2).
4.1
Equazione del moto dalla prima equazione cardinale
Per ricavare l’equazione del moto e il periodo T proprio di oscillazione del
pendolo il modo più semplice è di scrivere adeguatamente la seconda legge
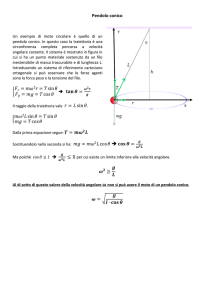
della dinamica per il punto materiale di massa m. Scomponendo la forza
peso m~g nelle due componenti mg cos θ ed mg sin θ rispettivamente parallela
e ortogonale al filo osserviamo che la prima è equilibrata dalla reazione
vincolare mentre la seconda fa muovere la massa lungo la traiettoria circolare
con velocità tangenziale v~τ il cui modulo è
dθ
dt
La seconda legge della dinamica si scrive allora
vτ = L
mg sin θ = m
3
dvτ
dt
(8)
(9)
Tenendo presente che l’incremento dθ produce un decremento nella velocità
ed eliminando la massa otteniamo
L
d2 θ
= −g sin θ
dt2
(10)
da cui risulta che il moto del pendolo dipende solo da L e g mentre è indipendente dalla massa. Il rapporto g/l ha dimensioni [T −2 ] come il quadrato
di una frequenza che viene indicato con ω02 . Mostriamo che ω0 risulta essere la pulsazione propria del pendolo valida per piccole oscillazioni ossia nel
limite in cui sin θ ∼ θ. Con le precedenti posizioni e indicando le derivate rispetto al tempo con il punto sovrapposto l’equazione (10) diventa la classica
equazione dell’oscillatore armonico
θ̈ + ω02 θ = 0
(11)
la cui soluzione è quindi
θ(t) = θ0 sin
2π
t+ϕ
T0
(12)
in cui si è utilizzata la relazione
2π
T0 =
= 2π
ω0
s
L
g
(13)
La verifica che la funzione del tempo (12) è soluzione della (11) risulta più
elegante se, utilizzando il formalismo complesso, poniamo
θ = θ0 ei(ω0 t+ϕ)
(14)
allora estraendo la derivata prima e seconda di θ rispetto al tempo
θ̇ = iω0 θ0 ei(ω0 t+ϕ) = iω0 θ
(15)
θ̈ = iω0 θ̇ = −ω02 θ
(16)
e
si vede che quest’ultima ha la forma della (11).
4.2
Le equazioni cardinali
Notiamo che per ricavare l’equazione del moto è stata sufficiente l’applicazione della prima sola (17) delle due equazioni cardinali valide per la dinamica
del punto materiale
F~ =
X
d~
p
F~i =
dt
~
dJ
~
=N
dt
dove per i simboli valgono le seguenti notazioni
4
(17)
(18)
• p~ ≡ m~v quantità di moto della particella;
• J~ ≡ ~r × p~ momento della quantità di moto;
~ ≡ ~r × F~ momento della forza;
• N
• ~r determina la posizione della particella rispetto ad un punto arbitrario
fisso scelto per il calcolo dei momenti delle forza e della quantità di
moto.
4.3
Il pendolo semplice e la seconda equazione cardinale
Anche se nel caso del pendolo semplice risulta superfluo, è istruttivo ricavare ulteriormente l’equazione del moto (11) dall’applicazione della seconda
equazione cardinale (18); nel caso del pendolo composto ciò risulterà necessario e pertanto lo consideriamo come conveniente introduzione. La seconda
equazione cardinale (18) esprime essenzialmente che la rapidità di variazione
del momento della quantità di moto è determinata dal momento delle forze.
Con riferimento alla Fig. 2 sia X l’asse normale al piano del moto ed O
il punto fisso per il calcolo dei momenti. La reazione vincolare ha momento
nullo mentre il momento della forza di gravità e il momento della quantità
di moto sono paralleli all’asse X con direzione contrarie. Avremo
Nx = (~r × F~ )x = −Lmg sin θ
(19)
Jx = (~r × p~)x = mL2 θ̇
(20)
e
ed ancora
dJx
= mL2 θ̈
dt
da cui applicando la seconda equazione cardinale (18)
mL2 θ̈ = −Lmg sin θ
(21)
(22)
che, dopo le ovvie semplificazioni, risulta uguale all’equazione (10) ottenuta
dalla prima equazione cardinale.
5
La soluzione completa per il periodo
Nella soluzione approssimata per le oscillazioni del pendolo semplice si è
visto come il periodo T0 delle piccole oscillazioni viene determinato da L e
g ma non dipende dall’ampiezza θ0 nel limite in cui sin θ ∼ θ.
Ci proponiamo adesso di illustrare il calcolo del periodo T del pendolo
semplice per una qualunque ampiezza −π ≤ θ ≤ +π. La procedura che
viene seguita, a partire dall’equazione dell’energia del sistema, costituisce un
5
ulteriore approccio al problema dell’equazione del moto. Scriviamo pertanto
la somma E dell’energia cinetica e potenziale del pendolo
1
E = mL2 θ̇2 + mgL(1 − cos θ)
2
(23)
che può essere riscritta come
θ̇2 = 2ω02 cos θ + C
(24)
avendo indicato con
ω02
g
=
l
; C=
2E
2g
−
mL2
L
(25)
Osserviamo che la costante C è legata alla massima ampiezza θ0 dalla
relazione
C
cos θ0 = −
(26)
2ω0
come può ottenersi dalla condizione θ̇ = 0.
Per il calcolo del periodo T osserviamo che esso è quattro volte il tempo
richiesto per passare da θ = 0 a θ = θ0 per cui riutilizzando la equazione (24)
che equivale a
q
dθ
= θ̇ = 2ω02 cos θ + C
(27)
dt
abbiamo che
Z θ0
T =4
0
dθ
4
=√
2
(2ω0 cos θ + C)
2ω0
Z θ0
0
dθ
(cos θ − cos θ0 )1/2
(28)
L’integrale (28) viene ricondotto ad un tipo ellittico introducendo una nuova
variabile definita da
sin(θ/2)
(29)
sin ψ =
sin(θ0 /2)
che permette di riscriverlo come
4
T =
ω0
Z π/2
0
dψ
(1 − sin (θ0 /2 sin2 ψ)1/2
(30)
2
L’integrale
Z π/2
0
dψ
(1 −
(31)
K 2 sin2 ψ)1/2
è chiamato integrale ellittico completo del primo tipo la cui soluzione in serie
di potenze è data da
Z π/2
0
dψ
π
=
2
1/2
2
2
(1 − K sin ψ)
(
1+
∞ X
1 · 3 · 5 · . . . · (2n − 1)
n=1
2 · 4 · 6 · . . . · (2n)
)
2
K
2n
(32)
6
Se scriviamo i primi termini della soluzione (32) otteniamo per il periodo
1
θ0
1 + sin2
4
2
T = T0
9
θ0
+
sin4
64
2
da cui si può facilmente calcolare che per θ0 ∼ 5◦ si ha
6
+ ...
(T −T0 )
T0
(33)
< 0.001.
Verifica delle leggi del pendolo semplice
Nella prima parte dell’esperienza si verificheranno le leggi del pendolo semplice e cioè che
1. il periodo T non dipende dalla massa;
2. le piccole oscillazioni sono isocrone;
3. T ∼ T0 è dato dalla equazione (13).
6.1
Materiale a disposizione
• Filo e sostegno
• Carta millimetrata
• Due cilindretti metallici di pari volume e diversa densità
• Cronometro di sensibilità σ = 0.01sec
• metro con sensibilità σ = 1mm
6.2
Procedura sperimentale
Per verificare che il periodo di oscillazione del pendolo è indipendente dalla
massa basterà confrontare i risultati delle misure ottenute per T1 e T2 relativi
a due pendoli aventi stessa lunghezza L e rispettivamente i due cilindretti
di peso differente come massa. Ci si aspetta ovviamente che T1 = T2 ± 2∆T.
Per rendere minimo l’errore ∆T si misurerà il tempo T = nT necessario per
compiere n oscillazzioni fissando n in modo tale da avere
∆T =
∆T
= 0.01sec
n
(34)
ossia ridurre l’errore sul periodo alla sensibilità del cronometro.
Per la verifica dell’isocronismo si confronteranno due periodi con ampiezza di oscillazione piccole ma differenti.
Quindi si procederà alla misura di alcune coppie (L, T ). Per la verifica
della relazione (13) osserviamo che essa può essere convenientemente riscritta
come
4π 2
T2 =
L
(35)
g
7
O
u
@
θ@
L
@
@
@
@xG
? mg
Figura 3: Pendolo composto
per cui riportando in grafico L versus T 2 ci si aspetta una retta passante
per l’origine di coefficiente angolare k dove valgono le seguenti relazioni
y = kx ; y ≡ T 2
4π 2
x≡L ; k=
g
(36)
(37)
Nel riportare in grafico i valori di x ≡ L si tenga presente che per la propagazione degli errori si ha che ∆y = 2T ∆T . Si calcoli graficamente la pendenza
della retta migliore e il relativo errore ∆k valutandolo dalle pendenze delle
due rette limite ancora compatibili con i dati sperimentali. Il valore di g e
il rispettivo errore ∆g saranno quindi determinati dalle relazioni
g = 4π 2 /k ; ∆g = ±g
7
∆k
k
(38)
Il pendolo composto
Per pendolo composto si definisce un qualsiasi corpo rigido pesante in grado
di ruotare senza attrito attorno ad un asse orizzontale non passante per il
baricentro (Fig. 3). Per lo studio del moto del sistema occorre scrivere la
seconda equazione cardinale (18) in cui i momenti vengono riferiti all’asse di
rotazione con la forza peso applicata al baricentro G del corpo. Osservando
che il momento della reazione vincolare è nullo e trascurando il momento
delle forze di attrito l’equazione del moto diventa
I
d2 θ
= −mgL sin θ
dt2
(39)
dove con I si è indicato il momento d’inerzia del pendolo rispetto all’asse di
rotazione.
8
L’equazione (39) è del tutto identica a quella ottenuta per il pendolo
semplice (13) con il periodo dato dall’espressione
s
T0 = 2π
I
= 2π
mgL
s
l
g
(40)
in cui la lunghezza
I
(41)
mL
prende il nome di lunghezza equivalente del pendolo composto.
Come si vede la misura indiretta di l attraverso la relazione (41) richiede
la conoscenza delle tre grandezze I, L, m delle quali solo l’ultima è di immediata misura mediante una bilancia. Nei paragrafi successivi illustreremo un
metodo che permette invece una misura diretta della lunghezza equivalente
del pendolo composto.
l=
7.1
Il pendolo di Kater a coltelli variabili
Nell’equazione (41) compare il momento I di inerzia del pendolo rispetto
all’asse di rotazione. Tale momento può essere calcolato facilmente se si
conosce il momento del sistema rispetto all’asse che passa per il baricentro.
Teorema 1 (Steiner-Huygens) Il momento d’inerzia I di un corpo rigido
rispetto ad un asse qualsiasi è uguale al momento d’inerzia IG del corpo
rispetto ad un asse parallelo al dato e passante per il baricentro G, aumentato
del prodotto della massa del corpo per il quadrato della distanza tra l’asse e
il baricentro.
Pertanto si ha I = IG + mL2 , da cui si ottiene per la lunghezza equivalente
del pendolo composto
l=
I
IG + mL2
IG
=
=L+
mL
mL
mL
(42)
Introduciamo adesso un particolare tipo di pendolo composto, costituito
essenzialmente da un’asta metallica omogenea, a cui sono stati praticati
una serie di fori O1 , O2 , . . . , On che servono a permettere all’asta di oscillare
attorno ad assi diversi (Fig. 4) (il pendolo reversibile).
Se consideriamo in particolare una coppia di tali assi, O ed O0 , le piccole
oscillazioni attorno ad essi saranno in genere caratterizzate da periodi di
diversa durata dati da
s
T = 2π
l
g
s
0
e T = 2π
l0
g
(43)
La condizione T 6= T 0 non è comunque vera in generale nel senso che è possibile trovare coppie di assi caratterizzati dallo stesso periodo delle oscillazioni
9
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
O1
O2
O
6
L
?
u
6
G
L0
?
On
Figura 4: Pendolo reversibile di Kater
assi coniugati; ma il costruttore del pendolo ha evitato di praticare i fori in
corrispondenza di tali assi coniugati.
Precisiamo che sono banalmente coniugati due assi posizionati simmetricamente rispetto al baricentro dell’asta ma che essi non risultano interessanti
ai fini dell’esperienza.
Se scriviamo infatti la condizione sotto cui T = T 0 ; dovendo dalla (43)
anche essere l = l0 otteniamo
IG
IG
L+
= L0 +
(44)
mL
mL0
da cui moltiplicando entrambi i membri per mLL0
mL0 L2 − (IG + mL02 )L + IG L0 = 0
(45)
otteniamo una equazione di secondo grado in L che ammette le due soluzioni
IG
(46)
mL0
La prima soluzione è quella banale priva di interesse per ulteriori sviluppi;
la seconda soluzione, che implica anche
L0 =
IG
mL
L = L0
e L=
−→
l =L+
10
IG
= L + L0
mL
(47)
O0
permette di associare la lunghezza equivalente del pendolo composto alla
distanza tra i due assi di oscillazione.
Quest’ultima relazione è di notevole interesse sperimentale fornendo un
metodo per la misura dell’accelerazione di gravità mediante il pendolo composto.
Avremo
l
g = 4π 2 2
(48)
T
dove l è la distanza tra due assi coniugati non banali ai quali corrisponde lo
stesso periodo di oscillazione T .
7.2
Misura di g con il pendolo reversibile
La relazione trovata per la lunghezza equivalente del pendolo reversibile,
per essere applicata alla misura di g, richiede una procedura sperimentale
che permetta la determinazione dei periodi e delle lunghezze equivalenti ad
esse associate a partire dalla misura del limitato numero di periodi delle
oscillazioni che è possibile realizzare con l’asta forata.
Si scelga un sistema di riferimento X solidale con l’asta ed orientato secondo la lunghezza dell’asta. Si determinino quindi le posizioni x1 , x2 , . . . , xn
dei fori O1 , O2 , . . . , On in tale sistema e si misurino i periodi T1 , T2 , . . . , Tn
corrispondenti.
Le coppie di dati (xi , Ti ) raccolte in tabella siano riportate in un grafico
T versus X. Si otterranno due archi di curva del tipo illustrato in Fig. 5
dove l’origine del sistema di riferimento è stata fissata coincidente con il
baricentro dell’asta la cui lunghezza totale è L = 100 cm.
I due rami di curva, ovviamente simmetrici rispetto al baricentro del
sistema, sono stati ottenuti dalla relazione
2π
T =√
g
s
2 x + L 12x (49)
che si riferisce al caso ideale di un pendolo lineare di lunghezza L.
Per un pendolo che si estende solo in lunghezza è facile calcolare il
momento di inerzia rispetto al baricentro e quindi il momento di inerzia
totale.
Indicando con λ = m/L la densità lineare dell’asta si ottiene
Z L/2
IG = 2
x2 dm = 2
0
Z L/2
0
λx2 dx =
mL2
12
(50)
e quindi per la lunghezza equivalente possiamo scrivere
l =x+
da cui è immediata la relazione (49).
11
L2
12x
(51)
2.00
T[sec]
`
`
`
`
`
`
`
`
`
`
`
1.75
```
T0
```
```
```
```
```
````
````
`````
````````````````````
```
``
`
``
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
`
``
`
-` ` `
l0
```
````
````````````````````
````
``
```
````
```
``
``
```
```
`
1.50
−50
−25
0.0
25
X[cm] 50
Figura 5: Periodo di un pendolo composto a coltello variabile
Se l’asse di oscillazione si avvicina al baricentro del sistema, che coincide
con il centro dell’asta, i periodi tendono all’infinito ossia il pendolo smette
di oscillare trovandosi in una condizione di equilibrio.
Per il pendolo a disposizione nella zona centrale non sono stati praticati
fori perchè per lente oscillazioni del sistema l’attrito del coltello all’interno
del foro non è più trascurabile; anche perchè il coltello è stato realizzato con
un semplice chiodo.
Nella Fig. 5 viene indicato graficamente una tipica lunghezza indicata
con l0 e il corrispondente valore di T0 .
Ovviamente i due rami di curva saranno definiti da un numero limitato
di punti sperimentali e ciascuno punto sarà affetto da errore di misura. Pertanto per la determinazione dei due parametri si richiede un procedimento
di interpolazione.
Per la valutazione dell’errore ∆T si tenga presente che l’intersezione di
due curve sperimentali avviene all’interno di un poligono determinato dalle
incertezze con cui sono note le grandezze graficate.
L’accelerazione di gravità sarà calcolata dalla relazione
g=
2π
T0
12
2
l0
(52)
mentre l’errore di g sarà
∆l0
∆T0
∆g = ±g
+2
l0
T0
(53)
Tra le infinite coppie (T0 , l0 ) ottenibili per interpolazione delle curve
sperimentali si determini quella che permette di ricavare la costante g con il
più piccolo errore ∆g.
I dati raccolti siano utilizzati per un confronto tra il periodo di oscillazzione previsto per il modello lineare di pendolo ideale e quello reale.
Valutare in particolare l’errore che si commetterebbe nella determinazione di g applicando la relazione (49) valida nel caso ideale.
A tale scopo si valuti il valore dell’accelerazione di gravità utilizzando
per il calcolo
2 L2 2π gi =
(54)
xi +
Ti
12xi Si ripeta il calcolo per tutte le coppie (xi , Ti ) disponibili in modo da poter
trattare statisticamente il valore di g e l’errore ∆g.
7.3
Il pendolo reversibile di Kater
Introduciamo adesso un particolare tipo di pendolo composto costruito in
modo da poter oscillare attorno a due fissati assi O ed O0 (Fig. 6) (il pendolo reversibile a coltelli fissi).
Diciamo subito che le grandezze fisiche
in gioco e le relazioni utili sono le stesse ricavate per il pendolo a coltelli
variabili. Con riferimento alla nuova geometria illustrata in Fig. 6 si ripercorra tutta la procedura che resta valida identicamente fino alla relazione
che lega la lunghezza equivalente del pendolo composto alla distanza tra due
assi di oscillazione. Quindi basta aggiungere quanto riportato nel paragrafo
seguente.
7.4
Misura di g con il pendolo reversibile
Nel pendolo reversibile di Kater le due masse M1 ed M2 scorrevoli permettono di variare la posizione del baricentro del sistema.
La relazione trovata per la lunghezza equivalente del pendolo reversibile
permette di determinare il valore dell’accelerazione di gravità g confrontando
i periodi di oscillazione attorno ai due assi per varie posizioni delle due
masse mobili. Il valore di T da utilizzare è quello corrispondente ad una
configurazione per cui si abbia T = T 0 ma diversa da quella banale L = L0 ;
la lunghezza equivalente l è sempre fissa ed uguale alla distanza tra i coltelli
ai quali il pendolo è incardinato per le oscillazioni. Mentre quest’ultima è
facilmente misurabile vediamo la procedura per determinare il periodo.
Le due masse mobili di cui è dotato il pendolo reversibile possono essere
posizionate l’una tra i due coltelli e l’altra all’esterno. Mantenendo fissa
13
M1
u
O
6
L
?
u
6
G
L0
M2
u
?
Figura 6: Pendolo reversibile di Kater
quella esterna, per ogni posizione relativa di quella interna si procede alla
misura dei due periodi relativi agli assi O ed O0 . Riportando in grafico i
periodi in funzione della distanza relativa delle due masse si ottengono due
curve la cui intersezione permette di determinare il valore di T0 cercato.
Ripetendo poi l’esperienza per altre posizioni della massa esterna ai coltelli
si può determinare la migliore intersezione delle due curve.
Per la valutazione dell’errore ∆T si tenga presente che l’intersezione
di due curve sperimentali avviene all’interno di un poligono determinato
dalle incertezze con cui sono note le grandezze graficate. Inoltre una volta
individuata la zona in cui T ∼ T 0 ulteriori punti sperimentali possono essere
acquisiti al fine di rendere minimo l’errore sul periodo. In quest’ultima fase
di raffinamento della procedura di misura si può far uso per le misure di
tempo del contatore al millesimo di secondo.
L’accelerazione di gravità e il relativo errore saranno calcolati utilizzando
le (52) e (53) rispettivamente.
14
O0
8
Oscillatore armonico smorzato
Un oscillatore armonico reale è soggetto, oltre alla forza elastica Fx = −kx,
a forze dissipative di varia origine che determinano lo smorzamento delle
oscillazioni. Un interessante esempio di smorzamento è quello dovuto ad
una forza di attrito di tipo Fa = −γ ẋ. L’equazione del moto diventa:
mẍ + γ ẋ + ω02 x = 0.
(55)
Si può verificare che una soluzione particolare è:
x(t) = X exp(−t/τ ) sin ωt,
(56)
dove valgono le seguenti relazioni:
m
τ =2 ;
γ
"
ω = ω0 1 −
1
ω0 τ
2 #1/2
.
(57)
L’ampiezza di oscillazione è soggetta ad un decremento esponenziale e la
pulsazione angolare diminuisce. Per lievi smorzamenti e quindi per valori di
τ T0 la pulsazione dell’oscillatore smorzato diviene ω ≈ ω0 .
La determinazione sperimentale della costante di decadimento esponenziale τ , della costante elastica k e dell’equivalente in massa della molla
permettono una verifica coerente della validità della Eq. (56).
9
Conclusioni
L’esperienza nel suo complesso presenta lo studio di un modello in fisica: l’oscillatore armonico. Il modello del pendolo semplice è intrinsecamente ideale
per il tipo di approssimazioni fatte sia sulla natura del filo (inestensibile e
privo di massa) che sulla massa propria considerata puntiforme.
Il modello del pendolo composto non richiede astrazioni anche se risultano sempre comode delle semplificazioni di natura geometrica come quella
di considerare un particolare modello esteso solo in lunghezza. Trattasi però
solo della scelta di un sistema comodo da trattare matematicamente e non
di una scelta inerente al modello di pendolo composto. In altre parole il
pendolo composto descrive in modo più completo i pendoli reali tenendo
conto dell’estensione e della distribuzione delle masse.
In entrambi i casi il modello di oscillatore armonico vale in regime di
piccole oscillazioni ed attriti trascurabili.
Per la massa sospesa ad una molla il regime di piccole oscillazioni non
viene richiesto esplicitamente, valendo il modello dell’oscillatore armonico
fin tanto che la forza elastica risulta lineare con le deformazioni. L’introduzione di un particolare tipo di forza dissipativa (Fa = −γ ẋ) nell’equazione
dell’oscillatore armonico allarga notevolmente le potenzialità descrittive del
modello.
15