Equilibrio di autoionizzazione dell`acqua Come già osservato l

Equilibrio di autoionizzazione dell’acqua
Come già osservato l’acqua presenta caratteristiche anfotere, potendosi comportare tanto da acido (con una
sostanza meno acida che si comporta da base) quanto da base (con una sostanza più acida).
Sappiamo inoltre che l'acqua distillata non è un buon elettrolita, cioè non conduce corrente elettrica, in quanto la
concentrazione di ioni presenti è estremamente bassa. Reagendo con sè stessa l’acqua presenta infatti il seguente
equilibrio di autoioniazzazione (detto anche semplicemente di dissociazione), molto poco spostato a destra:
dove sono contemporaneamente presenti le due coppie acido/base coniugata che abbiamo già incontrato.
L’equilibrio può essere considerato eterogeneo dal momento che la concentrazione dell’acqua reagente resta
praticamente invariata a seguito della dissociazione. Si può facilmente dimostrare che la concentrazione molare
dell’acqua pura è pari a 55,5 mol/L; tale valore resta praticamente invariato nella quasi totalità delle reazioni in
soluzione acquosa.
+
inizio
55,5 mol/L
0
0
Δ
-2x
+x
+x
equilibrio
55,5+2x
x
x
La costante di equilibrio si riduce al cosiddetto prodotto ionico dell’acqua
(dove w sta per water), costante a
temperatura costante come qualsiasi altra costante di equilibrio, pari a:
a 25°C
da cui si ricava che:
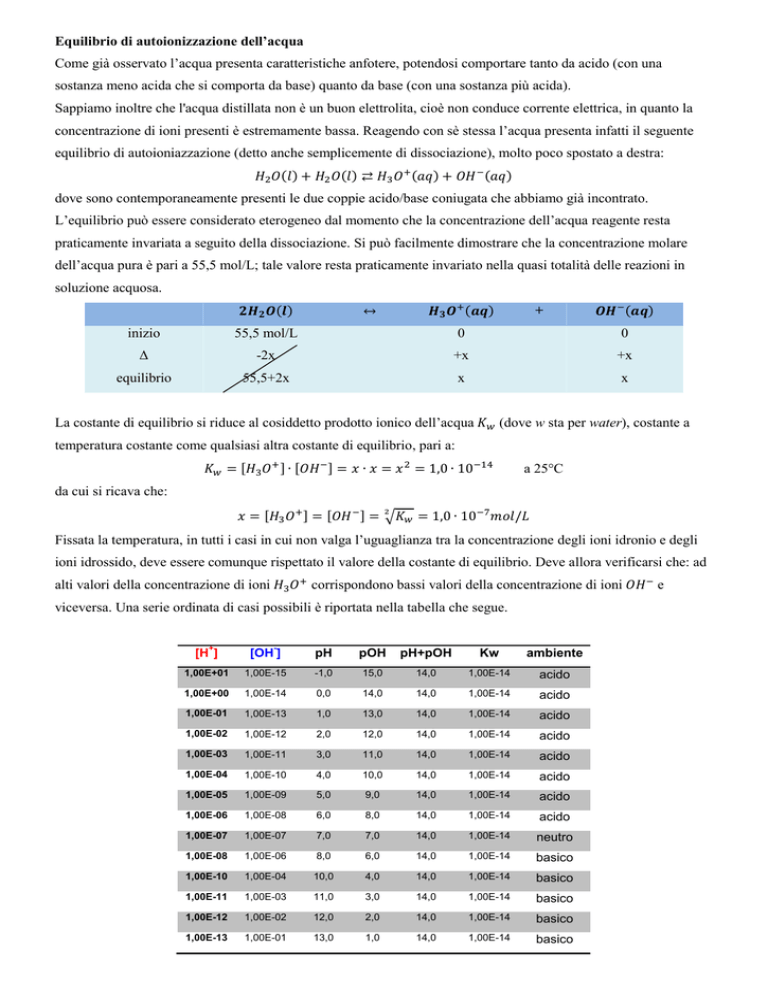
Fissata la temperatura, in tutti i casi in cui non valga l’uguaglianza tra la concentrazione degli ioni idronio e degli
ioni idrossido, deve essere comunque rispettato il valore della costante di equilibrio. Deve allora verificarsi che: ad
alti valori della concentrazione di ioni
corrispondono bassi valori della concentrazione di ioni
viceversa. Una serie ordinata di casi possibili è riportata nella tabella che segue.
+
-
[H ]
[OH ]
pH
pOH
pH+pOH
Kw
ambiente
1,00E+01
1,00E-15
-1,0
15,0
14,0
1,00E-14
acido
1,00E+00
1,00E-14
0,0
14,0
14,0
1,00E-14
acido
1,00E-01
1,00E-13
1,0
13,0
14,0
1,00E-14
acido
1,00E-02
1,00E-12
2,0
12,0
14,0
1,00E-14
acido
1,00E-03
1,00E-11
3,0
11,0
14,0
1,00E-14
acido
1,00E-04
1,00E-10
4,0
10,0
14,0
1,00E-14
acido
1,00E-05
1,00E-09
5,0
9,0
14,0
1,00E-14
acido
1,00E-06
1,00E-08
6,0
8,0
14,0
1,00E-14
acido
1,00E-07
1,00E-07
7,0
7,0
14,0
1,00E-14
neutro
1,00E-08
1,00E-06
8,0
6,0
14,0
1,00E-14
basico
1,00E-10
1,00E-04
10,0
4,0
14,0
1,00E-14
basico
1,00E-11
1,00E-03
11,0
3,0
14,0
1,00E-14
basico
1,00E-12
1,00E-02
12,0
2,0
14,0
1,00E-14
basico
1,00E-13
1,00E-01
13,0
1,0
14,0
1,00E-14
basico
e
1,00E-14
1,00E+00
14,0
0,0
14,0
1,00E-14
basico
1,00E-15
1,00E+01
15,0
-1,0
14,0
1,00E-14
basico
Il grafico relativo alla stessa tabella mostra un’iperbole equilatera molto schiacciata sugli assi, dal momento che il
valore della costante
è molto piccolo.
1,2E+01
[H3O+]
1,0E+01
[H3O ]∙[OH8,0E+00
]=1,0∙10-14
+
6,0E+00
4,0E+00
2,0E+00
0,0E+00
0,0E+00
5,0E+00
1,0E+01
[OH-]
Proprio per ovviare a valori così piccoli delle concentrazioni è molto usato il pH, definito come logaritmo negativo
della concentrazione molare degli ioni idronio:
I valori di pH ottenuti sono riportati nella terza colonna della stessa tabella riportata sopra: mentre i valori delle
variano da un minimo di 10-15 ad un massimo di 10, i corrispondenti valori di pH variano
concentrazioni di
da 15 a -1. Si può osservare come il pH coincida con l’esponente cambiato di segno della concentrazione di
espressa come potenza in base 10.
Analogamente in quarta colonna sono stati riportati i corrispondenti valori di pOH definito come segue:
Si possono presentare due casi opposti:
1) una soluzione acida per cui la concentrazione degli ioni idronio supera quella degli ioni idrossido e il pH è
minore di 7:
2) una soluzione basica per cui la concentrazione degli ioni idrossido supera quella degli ioni idronio e il pH è
maggiore di 7:
Dato che la maggior parte delle soluzioni impiegate in chimica sono acquose, l’acqua viene assunta come sistema
di riferimento in base al quale stabilire il grado di acidità di una soluzione.
se
acida
L’
è il
acqua
sistema di
riferimento
in base al
quale una
se
soluzione
si definisce
neutra
se
basica
per cui
[H3O+]>[OH-]
[H3O+]=[OH-]
pH<7
per cui
[H3O+]<[OH-]
pH=7
per cui
pH>7
La soluzione acida o basica può essere trattata come una perturbazione di una soluzione neutra per aggiunta di una
ben definita quantità di ioni
o di ioni
. Supponiamo ad esempio di aggiungere un certo numero di moli
a quelle già presenti in 1 L di acqua neutra (e quindi pari a 1,0∙10-7 mol). Applicando il principio
di ioni
dell’equilibrio mobile si avrà che:
+
inizio
1,0∙10-7 mol
perturbazione
+x
1,0∙10-7 mol
Δ
-y
-y
equilibrio
1,0∙10 mol+x-y
1,0∙10-7 mol -y
-7
A seguito della perturbazione l’equilibrio si sposta a sinistra, riducendo in ugual misura (-y) le quantità di ioni
e di ioni
. La perturbazione può essere facilmente osservata anche dal seguente grafico dove l’aggiunta
di ioni idronio allontana il sistema da un generico stato iniziale di equilibrio a fino al punto b. Il sistema torna alla
curva lungo un percorso che si muove su una retta di pendenza -1 e che lo porta al nuovo punto di equilibrio c.
12
b
10
ripristino
equilibrio
6
perturbazione
[H3O+]
8
4
2
c
a
0
0
2
4
6
8
10
12
[OH-]
Esercizi:
1) Dimostra che la concentrazione molare dell’acqua pura è legata alla sua densità e che risulta pari a 55,5 mol/L.
La densità dell’acqua a 25°C è pari a 1 g/mL.
………………………………………………………………………………………………………………………..
2) L’equilibrio di auto ionizzazione è endotermico. Come variano le concentrazioni degli ioni idronio e idrossido
all’aumentare della temperatura?
………………………………………………………………………………………………………………………..
3a) Qual è il pH di una soluzione in cui
a) 1,0∙10-11 M, b) 6,0∙10-4 M, c) 5,47∙10-8 M?
…………………………………………………………………………………………………………………………
3b) Qual è il pH di una soluzione in cui
d) 3,9∙10-12 M, e) 1,3∙10-3 M, f) 3,72∙10-6 M?
…………………………………………………………………………………………………………………………
La funzione logaritmo
Si dice logaritmo in base
di un numero
logaritmo). In altre parole, se:
l'esponente da dare ad a per ottenere
( viene chiamato argomento del
segue che:
Dove
e
sono numeri reali positivi, con
diverso da 1. Per esempio,
perché
.
Il logaritmo è utile soprattutto perché trasforma i prodotti in somme, i rapporti in differenze, gli elevamenti a
potenza in moltiplicazioni e i radicali in divisioni. Nel nostro caso particolare la funzione logaritmo è utile perché
trasforma numeri molto piccoli o molto grandi in un intervallo di valori molto più ristretto.
Esercizi: risolvi correttamente:
1)
2)
3)
4)
5)
6)
7)
8)
Calcolo del pH per soluzioni di acidi e basi forti
Vogliamo ora calcolare il pH di una soluzione che contiene una concentrazione data di un acido forte.
Consideriamo ad esempio una soluzione 0,1 M di acido cloridrico che ionizza completamente secondo la nota
reazione:
inizio
0,1 mol/L
55,5 mol/L
durante
-0,1 mol/L
(55,5-0,1) mol/L
fine
0
10-7 mol/L
+0,1 mol/L
(10-7+0,1) mol/L
+0,1 mol/L
+0,1 mol/L
Ancora una volta possiamo trascurare la presenza dell’acqua: se la concentrazione dell’acido Ca è maggiore di 10-4,
l’alta concentrazione di ioni idronio che si forma a seguito della ionizzazione acida reprime ulteriormente
l’autoionizzazione. Possiamo anche trascurare la presenza iniziale di una concentrazione idrogenioni pari a 10-7
mol/L, quantità trascurabile rispetto a quella che si forma per ionizzazione dell’acido. Si ottiene infine che:
0,1 mol/L e pH = 1.
Proviamo a calcolare il pH di una soluzione acquosa di una base frte come NaOH. La reazione di dissociazione
risulta:
inizio
0,1 mol/L
55,5 mol/L
durante
-0,1 mol/L
(55,5-0,1) mol/L
10-7 mol/L
0
fine
+0,1 mol/L
(10-7+0,1) mol/L
+0,1 mol/L
+0,1 mol/L
Trascuriamo allo stesso modo la presenza dell’acqua (Cb>10-4 mol/L) e la piccola concentrazione iniziale di ioni
idrossido. La concentrazione finale è allora
mentre
ed il pH sarà pertanto pari a 13.
Nel caso di un acido forte diprotico come l’acido solforico il calcolo del pH parte dalla seguente reazione di
ionizzazione (non abbiamo considerato la presenza dell’acqua e posto nulla la concentrazione iniziale di ioni
inizio
0,1 mol/L
0
0
durante
-0,1 mol/L
+0,1 mol/L
+0,2 mol/L
0
+0,1 mol/L
+0,2 mol/L
fine
La concentrazione finale di ioni idronio è allora doppia rispetto a quella iniziale di acido, pertanto:
Il pH risulta correttamente inferiore a 1.
Nella tabella che segue sono ordinati i principali acidi e basi forti di uso comune.
Nome
Acido perclorico
Acido nitrico
Acido solforico
Acido cloridrico
Acido bromidrico
Acido iodidrico
idrossido di sodio
Idrossido di potassio
Idrossido di calcio (poco solubile)
Idrossido di magnesio (poco solubile)
formula
:
Esercizi:
1) Calcola il pH di una soluzione 0,5 M di HCl
…………………………………………………………………………………………………………………
2) Calcola il pH di una soluzione ottenuta aggiungendo a 5 L di acqua 100 g di NaOH solido.
…………………………………………………………………………………………………………………
3) Calcola il pH di una soluzione di idrossido di alluminio Al(OH)3, base forte (attenzione perché libera tre ioni
idrossido!)
…………………………………………………………………………………………………………………
4) Calcola il pH di una soluzione ottenuta a partire da 20 mL di una soluzione 0,2 M di acido nitrico diluita con 200
mL di acqua (considera i volumi additivi).
…………………………………………………………………………………………………………………
5) Qual è il pH di una soluzione che si ottiene sciogliendo 0,0025 mol di NaOH in acqua fino a ottenere un volume
complessivo pari a 250 mL?
………………………………………………………………………………………………………………………….
6) In laboratorio è stato assegnato il compito di diluire 10 mL di una soluzione acquosa di
al fine di
preparare una soluzione con pH=3. Come intendi procedere?
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
7) Completa la seguente tabella con tutte le informazioni e i concetti appresi
HCl
HCl
HCl
HCl
(0,1M)
(0,01)
(0,001)
(0,0001)
acqua
NaOH
NaOH
NaOH
NaOH
(0,0001)
(0,001)
(0,01)
(0,1)
7
pH
blu
Tornasole
Metilarancio
Incolore
Fenolftaleinina
Calcolo del pH per soluzioni di acidi deboli e basi deboli
Nell’ipotesi in cui l’acido o la base siano deboli, il calcolo del pH richiede la risoluzione di un problema di
equilibrio. Supponiamo di voler calcolare il pH di una soluzione di acido acetico 0,1 M, che ionizza parzialmente
secondo la seguente reazione (trascuriamo, al solito, l’autoprotolisi dell’acqua):
inizio
0,1 mol/L
55,5 mol/L
durante
-x mol/L
(55,5-x) mol/L
10-7 mol/L
0
equilibrio
+x mol/L
(10-7+x) mol/L
+x mol/L
+x mol/L
inizio
0,1 mol/L
0
0
durante
-x mol/L
+x mol/L
+x mol/L
0,1-x
+x mol/L
+x mol/L
fine
L’espressione della
dell’acido acetico risulta allora:
Sostituendo i valori delle concentrazioni all’equilibrio si ha che:
Se la
e la concentrazione iniziale dell’acido soddisfano le seguenti condizioni:
<
possiamo
trascurare anche la piccola ionizzazione acida rispetto alla concentrazione iniziale di 0,1 mol/L e il calcolo si riduce
a:
che risolto rispetto a x da:
da cui il pH:
Il pH ottenuto è più alto di quello ottenuto da una soluzione di un acido forte 0,1M.
La formula semplificata per il calcolo del pH di una soluzione contenente un acido debole è:
dove
è la concentrazione iniziale dell’acido e
la sua costante di ionizzazione acida.
Il calcolo del pH di una soluzione ottenuta a partire da una base debole è analogo. Consideriamo come base debole
l’ammoniaca e scriviamo innanzitutto la sua reazione di ionizzazione:
la cui costante vale:
All’equilibrio si avrà che:
inizio
0,1 mol/L
0
0
durante
-x mol/L
+x mol/L
+x mol/L
0,1-x
+x mol/L
+x mol/L
fine
Proprio come per la ionizzazione acida dell’acido acetico, la concentrazione di ioni idrossido è facilmente
ricavabile come segue:
Il calcolo del pH porta al seguente risultato:
Il pH ottenuto è nettamente più basso di quello di una soluzione 0,1 M di una base forte (pari a 13).
Riportiamo nella tabella che segue alcuni acidi e basi deboli con i rispettivi valori delle costanti acide e basiche di
ionizzazione.
Nome
formula
Ka/Kb
Acido solforoso
1,5∙10-2
Acido fosforico
7,5∙10-3
Acido fluoridrico
7,1∙10-4
Acido nitroso
4,5∙10-4
Acido acetico
1,8∙10-5
Acido solfidrico (prima ionizzazione)
1,0∙10-7
Acido cianidrico
4,0∙10-10
metilammina
6,5∙10-5
ammoniaca
1,8∙10-5
idrazina
1,7∙10-6
urea
1,3∙10-14
Le formule da usare nei 4 diversi casi esaminati per il calcolo della concentrazione idrogenionica e del pH sono
riproposte nella tabella che segue:
soluzione di
Dati a disposizione
Acido forte
Base forte
Acido debole
Base debole
Esercizi
1)
Calcola il pH di una soluzione 0,3 M di acido acetico.
.........................................................................................................................................................................
2)
Calcola la concentrazione iniziale di acido acetico se la soluzione che lo contiene presenta pH=5
……………………………………………………………………………………………………………….
3)
Calcola il pH di una soluzione di urea 0,4 M.
…………………………………………………………………………………………………………………
4)
Calcola la concentrazione iniziale di idrazina sapendo che il pH è 8
…………………………………………………………………………………………………………………
5)
Considera le seguenti soluzioni acquose elencate e ordinale in base al pH crescente.
a)
0,1 M
b)
0,1 M
c)
0,1 M
d)
0,001 M
e)
1M
…………………………………………………………………………………………………………………………
6)
Quale è il pH di una soluzione di HF con concentrazione 0,50 M? (la
) [1,88]
………………………………………………………………………………………………………………………….
7)
Su una bottiglia che contiene una soluzione è riportata la seguente indicazione
. Uno
studente preleva 100 mL di questa soluzione e ne calcola il pH. Qual è il suo valore?
………………………………………………………………………………………………………………………….
8)
Il pH di 200 mL di un acido debole 0,5 M vale 2,8. Il pH di 100 mL di un acido debole 0,5 M vale 3,1.
Quale acido è il meno debole? Calcola le costanti di ionizzazione acida per i due acidi e confrontale.
………………………………………………………………………………………………………………………….