Mobilit`a apparente e coefficiente di riflessione in nano

UNIVERSITÀ DEGLI STUDI DI UDINE
Facoltà di Ingegneria
Corso di Laurea Specialistica/Magistrale in
Ingegneria Elettronica
Dipartimento di Ingegneria Elettrica,
Gestionale e Meccanica
Tesi di Laurea
Mobilità apparente e coefficiente di
riflessione in nano-transistori MOS
quasi-balistici
Relatore:
Laureando:
Prof. Ing. David Esseni
Massimiliano Zilli
Correlatori:
Chiar.mo Prof. Ing. Luca Selmi
Prof. Ing. Pierpaolo Palestri
Anno Accademico 2005-06
Indice
1 Introduzione
1.1 Uno sguardo all’evoluzione della microelettronica . . . . . . .
1.2 La legge di Moore e lo scaling . . . . . . . . . . . . . . . . . .
1.3 Scopo della tesi . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1
2
4
2 Il transistore MOS
2.1 Il transistore MOS tradizionale . . . . . . . . . . . .
2.2 Mobilità di canale lungo . . . . . . . . . . . . . . . .
2.3 Il transistore MOS in regime balistico . . . . . . . .
2.4 Mobilità balistica . . . . . . . . . . . . . . . . . . . .
2.5 Corrente in dispositivi decananometrici . . . . . . .
2.6 Mobilità nei dispositivi decananometrici . . . . . . .
2.7 Estrazione sperimentale del coefficiente di riflessione
2.7.1 Generalizzazione del metodo di estrazione . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7
7
9
10
12
13
15
23
24
3 Simulatore Monte Carlo
3.1 L’equazione del trasporto di Boltzman . . . .
3.2 Simulazioni Monte Carlo . . . . . . . . . . . .
3.2.1 Simulazione del moto di una particella
3.3 Quantizzazione verticale in strutture MOS . .
3.4 Simulatore CoSMOS2D . . . . . . . . . . . .
3.4.1 Meccanismi di scattering in CoSMOS
3.4.2 Modello per i contatti . . . . . . . . .
3.4.3 Descrizione dell’input file . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
29
29
32
33
37
38
41
46
48
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Simulazione della mobilità apparente in transistori decananometrici
51
4.1 Estrazione della mobilità dalle simulazioni . . . . . . . . . . . 51
4.1.1 Mobilità apparente . . . . . . . . . . . . . . . . . . . . 51
4.1.2 Mobilità di canale lungo . . . . . . . . . . . . . . . . . 52
4.2 Mobilità di singola sottobanda . . . . . . . . . . . . . . . . . 53
4.3 Mobilità per dispositivi strain . . . . . . . . . . . . . . . . . . 60
4.4 Mobilità al variare della temperatura . . . . . . . . . . . . . . 64
I
5 Simulazione della metodologia di estrazione sperimentale
del coefficiente di riflessione
5.1 Profilo di potenziale lineare . . . . . . . . . . . . . . . . . . .
5.2 Profilo di potenziale lineare con virtual source . . . . . . . . .
5.3 Simulazione di un dispositivo completo . . . . . . . . . . . . .
67
67
74
82
6 Conclusioni
89
II
Capitolo 1
Introduzione
1.1
Uno sguardo all’evoluzione della microelettronica
The future of integrated electronics
is the future of electronics itself ...
Gordon E. Moore, 1965
Con questa frase iniziava l’articolo di Gordon E. Moore [2], uno dei fondatori
di Intel, scritto nel 1965, uno dei documenti storicamente più importanti e
lungimiranti nell’evoluzione dell’elettronica. In esso, oltre all’enunciazione
della celebre legge di Moore, ci sono molte intuizioni che nell’arco del tempo
sono state confermate. L’elettronica integrata ha infatti proceduto migliorando le figure di merito dei circuiti per mezzo di una continua contrazione
delle dimensioni geometriche dei transistori. Oggigiorno i computer portatili sono cosa comune, ma vent’anni fa praticamente non esistevano; gli
stessi personal computer da scrivania erano ingombranti e computazionalmente poco potenti. Oltre a questo, il documento di Moore affronta gli
aspetti economici legati alla miniaturizzazione facendo notare come l’elettronica integrata consenta un deciso abbattimento dei costi di produzione.
Dal grafico di figura 1.1 si vede infatti che l’andamento del costo per componente al variare del numero di componenti per circuito integrato ha un
minimo. Si vede inoltre che tale minimo decresce col passare del tempo e
che in tale minimo il numero di componenti per circuiti integrati aumenta
in modo impressionante con l’evoluzione della tecnologia di fabbricazione.
Con il continuo aumento delle prestazioni e quindi della capacità di elaborazione si arriverà presto a realizzare applicazioni fino a pochi anni fa dal
sapore futuristico ed esotico come le traduzioni linguistiche in tempo reale,
il riconoscimento facciale istantaneo e la guida automatizzata di automobili.
1
Figura 1.1: Curve del costo per componente al variare del numero di componenti per circuito integrato per gli anni 1962 e 1965, con la proiezione per
il 1970. [2]
1.2
La legge di Moore e lo scaling
La sorprendente capacità visionaria di Moore è sintetizzata dalla cosiddetta
“Legge di Moore”. Infatti, oltre ad intuire la modalità di sviluppo dell’elettronica nei vari ambiti (cosa certamente non banale), Moore teorizzò che il
numero di transistori su un chip sarebbe raddoppiato ogni due anni. Tale
previsione si è avverata nei quaranta anni che hanno seguito la sua formulazione e la tendenza all’aumento del numero di transistori è tuttora in
corso.
L’aumento costante della integrazione è stato possibile grazie allo scaling,
ovvero alla riduzione delle dimensioni dei dispositivi. Allo scaling, infatti,
ha corrisposto un costante miglioramento delle prestazioni dinamiche dei
circuiti digitali, mentre l’aumento delle frequenze di lavoro ha progressivamente reso il contenimento della potenza dissipata uno dei più vincolanti
problemi di progetto. Infatti, oggigiorno la maggior parte delle persone ha
nelle proprie tasche, forse inconsapevolmente, dei veri e propri computers
che sono alimentati a batteria e possono funzionare per alcuni giorni senza
bisogno di essere caricati. Per queste applicazioni, quindi, un uso efficiente
della potenza assorbita dal circuito risulta cruciale.
Il concetto di scaling è schematicamente indicato in figura 1.3. Oltre
a problemi tecnologici nella fabbricazione di dispositivi sempre più piccoli,
si sono presentati molti problemi che ne possono limitare lo scaling. Fra i
principali di essi si citano:
2
Figura 1.2: Andamento della legge di Moore nel mercato dei microprocessori.
[1]
• l’aumento della potenza dissipata ed in particolare della densità di
potenza (cioè della potenza per unità di area);
• il degrado delle prestazioni dei transistori dovuto alle dimensioni sempre minori; problema noto col termine di effetti di canale corto;
• l’insorgenza di una corrente statica al gate dei transistori MOSFET
provocata dal progressivo ridursi dello spessore dell’ossido di gate;
• problemi affidabilistici che degradano le caratteristiche dei transistori nel tempo di utilizzo, principalmente legati all’aumento dei campi
elettrici all’interno dei dispositivi stessi.
Un metodo sinergico rispetto allo scaling geometrico per ottenere un
miglioramento delle prestazioni dei dispositivi è l’introduzione di nuovi materiali rispetto al silicio ed al relativo ossido (SiO 2 ) che sono tradizionalmente
usati per i transistori MOSFET. I nuovi materiali riguardano l’isolante di
gate dei transistori MOS attraverso l’introduzione di materiali high-k ad alta
costante dielettrica. Un vasto campo di studio riguarda inoltre il materiale
del canale del transistore. Basti pensare all’uso della tensione o compressione meccanica del silicio per migliorarne la mobilità o anche all’uso di
semiconduttori alternativi come il germanio o l’arsenurio di gallio.
3
Figura 1.3: Regole dello scaling
1.3
Scopo della tesi
Spingendo sempre di più lo scaling geometrico si sono raggiunte lunghezze
paragonabili al libero cammino medio percorso dai portatori tra due eventi di scattering. In questo modo il dispositivo si avvicina ad un regime di
trasporto semi-balistico, dove per regime completamente balistico intendiamo un trasporto completamente privo di scattering tra source e drain, in
questo contesto consideriamo eventi di scattering tutte le interazioni che un
portatore subisce durante il suo moto a causa della deviazione del potenziale
in cui viaggia rispetto al potenziale di un cristallo di semiconduttore ideale.
I modelli di trasporto più diffusi (universalmente utilizzati, ad esempio, in
simulatori per l’ambito industriale) sono basati su un modello di trasporto
di tipo ohmico-diffusivo (noto come drift-diffusion). Anche la maggior parte
delle tecniche di caratterizzazione sperimentale sono state concepite in base
ad una descrizione del dispositivo fondata sul modello ohmico-diffusivo. Per
i dispositivi di odierna concezione, quindi, sorge la necessità di valutare l’effetto del trasporto semi-balistico sulle grandezze estratte dalle tecniche di
caratterizzazione tradizionali, come la mobilità apparente di canale. Inoltre,
nel modello di trasporto semibalistico la corrente nel dispositivo è governata dalla carica al punto di iniezione nel canale (detto virtual source) e dal
coefficiente di riflessione del canale del transistore. Data l’importanza del
coefficiente di riflessione, sono state proposte tecniche di caratterizzazione
per la sua determinazione sperimentale.
In questa tesi, mediante l’uso di un simulatore numerico di tipo Monte
Carlo che permette di risolvere l’equazione del trasporto di Boltzmann senza ipotesi semplificative, analizzeremo innanzitutto l’estrazione della mo4
bilità in transistori decananometrici. Discuteremo il significato stesso della
grandezza estratta rimarcando che si tratta di una mobilità apparente che
dipende dalla lunghezza del dispositivo in cui è misurata, diversamente dalla mobilità legata al trasporto uniforme che può essere determinata solo in
transistori abbastanza lunghi. Inoltre sarà derivato e discusso un modello
analitico approssimato che giustifica la dipendenza della mobilità apparente dalla lunghezza e dalla temperatura. Nella seconda parte di questo
lavoro useremo il simulatore Monte Carlo per emulare la determinazione del
coefficiente di riflessione in base ad un metodo di caratterizzazione proposto in letteratura. I valori del coefficiente di riflessione estratti secondo la
metodologia proposta verranno confrontati con quelli forniti dal simulatore
stesso in base ad un’analisi microscopica basata sui flussi di portatori interni al dispositivo. Questo confronto consentirà di valutare l’attendibilità
dei risultati della tecnica di caratterizzazione e la criticità di alcune ipotesi
su cui essa è basata. In questo contesto si sottolinea l’aspetto di innovatività
nell’uso del simulatore Monte Carlo per analizzare le tecniche di caratterizzazione; un uso divenuto indispensabile per dispositivi decananometrici,
dove il regime di trasporto è semibalistico e l’uso dei simulatori commerciali
basati sul modello ohmico-diffusivo perde quindi di attendibilità.
5
6
Capitolo 2
Il transistore MOS
In questo capitolo si parte esponendo il comportamento del MOS nel modello tradizionale, per poi introdurre una descrizione del MOSFET completamente balistico. Si va quindi ad esporre un modello per un moderno MOSFET decananometrico mediante il coefficiente di riflessione. Nell’ambito di
queste trattazioni si affronterà anche il tema della mobilità.
2.1
Il transistore MOS tradizionale
Il trasporto all’interno di un MOSFET tradizionale può essere descritto bene
mediante le equazioni drift-diffusion. Esso è la soluzione dell’equazione di
Boltzmann mediante il metodo dei momenti facendo l’approssimazione che
l’elettrone e il reticolo abbiano la stessa temperatura ovvero fermandosi al
momento di ordine uno delle equazioni di Boltzmann. Tale modello può
essere applicato in situazioni in cui il campo elettrico lungo il canale è moderatamente alto. In tal modo, vedi figura 2.1, gli eventi di scattering sono
troppo frequenti per permettere all’elettrone di acquisire oltre una certa velocità, ovvero di uscire dalla condizione di equilibrio tra la forza esercitata
dal campo elettrico e la forza resistente prodotta dagli eventi di scattering. Questo permette di asserire che la velocità degli elettroni è univocamente legata al campo elettrico longitudinale in direzione del trasporto.
L’equazione che esprime la densità di corrente è
Jn = −qµn n∇φ + qDn ∇n
(2.1)
dove µn è la mobilità elettronica, q la carica, n la concentrazione degli elettroni, Dn il coefficiente di diffusione elettronica legato alla mobilità µ n mediante la relazione di Einstein Dn = µn VT H e φ il potenziale. Avendo
l’equazione (2.1) due incognite è necessario introdurre anche l’equazione di
Poisson che definisce il potenziale
+
∇ · (∇φ) = −ρ = −q p − n + ND
− NA−
7
(2.2)
Scattering events
Source
E C (x)
F
x
Drain
x
Figura 2.1: Raffigurazione del funzionamento di un MOSFET tradizionale.
Lungo il canale il campo elettrico non è abbastanza forte da permettere
all’elettrone di acquisire l’energia per uscire dall’equilibrio.
+
dove ρ è la densità di carica, p è la concentrazione delle lacune, N D
è la
−
concentrazione di atomi donori ionizzati e N A è la concentrazione di atomi
accettori ionizzati. É possibile scrivere un’equazione simile alla (2.1) anche
per le lacune. Nel caso di un MOSFET con canale lungo (vedi figura 2.2),
integrando lungo la direzione della profondità di canale, y, e lungo la sua
larghezza, z, è possibile pervenire alla formula della corrente per il MOS di
canale lungo
ID =
1 2
W
µ0 COX (VGS − VT ) VDS − VDS
L
2
(2.3)
dove µo è la mobilità media degli elettroni nello strato invertito (ovvero la
mobilità pesata con la concentrazione degli elettroni lungo y), C OX è la
capacità per unità di superficie dell’ossido di gate, W è la larghezza del
dispositivo, L la lunghezza del canale, V GS la tensione tra gate e source e
VDS la tensione tra drain e source. Da questa espressione si può ricavare
l’espressione della corrente in regime lineare ovvero quella per basse V DS
ID =
W
µ0 COX [(VGS − VT ) VDS ]
L
8
(2.4)
L
z
x
y
Gate
W
Oxide
Source
Drain
Substrate
Figura 2.2: Schema rappresentativo della struttura di un MOSFET con il
sistema di riferimento utilizzato.
Analogamente per tensioni tra source e drain elevate, ovvero per le normali
condizioni di lavoro di un dispositivo, si ha la corrente di saturazione
ID,sat =
2.2
W
µ0 COX (VGS − VT )2
2L
(2.5)
Mobilità di canale lungo
La mobilità elettronica di canale lungo è un parametro molto importante per
la determinazione delle prestazioni dei transistori MOS. Il significato fisico
della mobilità si comprende osservando che, applicando un debole campo
elettrico fra drain e source del MOSFET, gli elettroni si muovono con moto
di deriva la cui velocità è appunto proporzionale al campo elettrico attraverso
la mobilità. Possiamo quindi affermare che la mobilità media nello strato di
inversione è definita come [29]
µ=
L gd (VG )
W qNs (VG )
(2.6)
dove gd (VG ) è la conduttanza di drain (la quale dipende dalla tensione di
gate VG ), q è la carica dell’elettrone, ed N s indica la densità di inversione
definita come:
Z
qNs (VG ) =
VG
−∞
CG C(VG0 )dVG0
(2.7)
Da un punto di vista fisico la mobilità dipende dal tempo di rilassamento
della quantità di moto ovvero dalla media tra gli intervalli tra uno scattering
e l’altro all’interno del dispositivo. I principali meccanismi di scattering nel
transistore MOSFET sono:
9
• Scattering fononico (acustici e ottici);
• Scattering con l’interfaccia fra semiconduttore ed ossido;
• Scattering con impurità ionizzate;
2.3
Il transistore MOS in regime balistico
Una descrizione molto diversa rispetto a quella usata per il MOSFET tradizionale
è necessaria per il transistore balistico. In questo caso infatti il gas elettronico responsabile della corrente è in forte non equilibrio con il reticolo
cristallino perchè non abbiamo eventi di scattering durante il passaggio della particella all’interno del canale. Col ridursi della lunghezza dei dispositivi,
come si vedrà nelle sezioni successive, ci si avvicina a questo limite teorico grazie al fatto che la lunghezza di canale è sempre più piccola rispetto
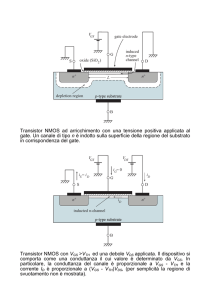
al libero cammino medio dell’elettrone. A questo proposito, figura 2.3, il-
Figura 2.3: Andamento qualitativo della banda di conduzione all’interno del
MOSFET al variare di VG per alte tensioni VD applicate
lustra il profilo qualitativo della più bassa sottobanda, la first unprimed,
lungo il canale per un MOSFET. Nella figura sono mostrate diverse curve al
variare di VG . Si può notare come il massimo di potenziale lungo il canale
diminuisca all’aumentare di VG . Anche a VG alte, comunque, dopo il source è
presente un massimo della sottobanda che viene denominato source virtuale.
Questo punto è molto importante per il funzionamento del MOS in regime
10
balistico. Infatti la densità di carica di inversione Q IN V (0) al virtual source
è approssimativamente determinata elettrostaticamente dalla tensione V G
come
QIN V (0) ≈ Cef f (VGS − VT )
(2.8)
La carica presente al virtual source proviene dai contatti di drain e source
che possono essere considerati con buona approssimazione come delle riserve
di carica all’equilibrio. Al virtual source, come schematizzato da figura 2.4,
E(k x )
EF
E F−qV DS
−k x
+k x
E C (x)
Figura 2.4: Distribuzione della popolazione di carica al virtual source. Si
sottolinea come la differenza di riempimento della parabola nella parte delle
velocità negative dipenda dalla tensione V DS [13].
saranno quindi presenti due tipi di popolazioni elettroniche, una con k x
negativi provenienti dal drain che ha livello di Fermi e una con k x positivi
provenienti dal source. In generale quindi possiamo esprimere la corrente
(i)
per la i-esima sottobanda ID come [7]
(i)

ID
q
= 2
W
h̄
s
(i)
mC
2
KT
π
3
2

 = 1 (η (i) ) − = 1 (η (i) )
S
D
2
2
(2.9)
analogamente possiamo esprimere la densità di inversione come
(i)
N2D
(i)
mD KT (i)
(i)
=
=0 (ηS ) + =0 (ηD )
2 2
πh̄
"
#
(i)
(2.10)
Nelle due equazioni sopra riportate m C è la massa effettiva di conduzione
(i)
mentre mD è la massa effettiva della densità degli stati. Nel caso della first
11
q
(i)
unprimed si ha mD = 2mt e
(i)
q
(i)
q
(i)
(i)
mC = 2 mD /mx = 2 mD /mt =
√
4mt
ovvero mD = 2mt . Il simbolo =j (η) indica l’integrale di Fermi-Dirac di
ordine j ed è definito da:
=j (η) =
1
Γ(1 + j)
Z
uj
du
1 + eu−η
+∞
0
(2.11)
dove Γ è la funzione gamma dipendente da j. Per lo scopo di questa tesi
√
√
è sufficiente ricordare i valori Γ(1/2) = π, Γ(3/2) = π/2 e Γ(1) = 1.
(i)
(i)
Gli argomenti delle suddette funzioni sono η S = (EF − E (i) )/KT e ηD =
(i)
(EF −E −qVD )/KT , dove EF è il livello di Fermi al source oppure al drain
(i)
(i)
(per ηS ed ηD rispettivamente) e E (i) è l’energia dell’autovalore i-esimo.
Nel caso di tensioni VD applicate sufficientemente elevate è possibile
considerare nullo il contributo di carica proveniente dal drain, essendo molto
improbabile trovare all’equilibrio cariche con energia tale da superare la
barriera del canale. Si possono scrivere quindi (2.9) e (2.10) come
(i)

ID ∼  q
=
W
h̄2
(i)
N2D
s
(i)
mC
2
"
KT
π
(i)
3
2

 = 1 (η (i) )
2
S
#
mD KT
(i)
=0 (ηS )
=
πh̄2 2
(2.12)
(2.13)
Siccome la corrente può anche essere espressa come
(i)
ID
(i) (i)
= qN2D vinj
W
(2.14)
sostituendo le (2.12) e (2.13) in (2.14) si può ottenere la velocità di iniezione
vinj al virtual source:
(i)
vinj
(i)
v
u
= 1 (ηS )
u 2KT = 12 (ηS )
= vth 2
=t
(i)
πmL =0 (ηS )
=0 (ηS )
(2.15)
dove mL è la massa in direzione longitudinale al canale della i-esima sottobanda. Questa non è altro che la velocità termica del caso non degenere
moltiplicata per il coefficiente che tiene conto della degenerazione.
2.4
Mobilità balistica
Vediamo adesso l’espressione assunta dalla grandezza:
L gd (VG )
W qNs (VG )
12
(2.16)
che, secondo l’equazione (2.6) definisce la mobilità nei transistori con canale
lungo. Prendendo nuovamente la (2.9) valida anche in caso di bassi campi
si ottiene
s
q2
gd
= 2
W
h̄
(i)
mC KT
= 1 (ηS )
2 π −2
(2.17)
Sostituendo (2.17) e (2.10) (valutata per tensione V DS = 0), nella (2.6) otteniamo una mobilità apparente nei transistori corti, che chiamiamo mobilità
balistica ed indichiamo col simbolo µ B
s
(i)
=− 1 (ηS )
qL =− 21 (ηS )
mL π =− 21 (ηS )
2
=
=
µ
L
BAL,L
(i)
(i)
2KT
=
(η
)
=
(η
)
=
0 S
0 (ηS )
πmL
πmL vth 0 S
(2.18)
Come si può notare questa mobilità è ben diversa dalla classica mobilità di
canale lungo. Inoltre da notare che è tanto più elevata tanto più lungo è il
dispositivo e risulta proporzionale alla lunghezza di canale L del dispositivo.
µB =
2.5
qL
Corrente in dispositivi decananometrici
Nei dispositivi di nuova generazione la trattazione delle equazioni DriftDiffusion non è più attendibile. In questi dispositivi, infatti, la distribuzione
in energia delle cariche non è più una funzione locale del campo elettrico
come si vedrà nel capitolo 3. La figura 2.5 raffigura in modo schematico
Gate
Source
Drain
Figura 2.5: Schematizzazione del funzionamento di un MOSFET mediante
flussi. Da sinistra si vede arrivare il flusso proveniente dal source, da destra
quello proveniente dal drain.
una visione del trasporto basata sulla teoria dei flussi di portatori (o flux
theory). Il drain e il source vengono visti come delle riserve che iniettano
13
flussi di portatori nel canale attraverso una barriera di potenziale che viene
modulata dalla tensione di gate. Il massimo di questa barriera è il virtual
source. In condizioni di alte VDS si può ritenere il flusso uscente dal drain
nullo senza commettere un errore rilevante. La situazione in esame viene
[SS]
aS
[SC]
aC
aD
bC
Figura 2.6: Modello del MOSFET utilizzato valido in condizioni di saturazione. La prima sezione descrive la trasmissione di cariche dal source al
canale, la seconda la trasmissione attraverso il canale. Questo modello fa
l’approssimazione, valida in condizione di saturazione, che il flusso in arrivo
dal drain non riesce a trasmettersi al source. [9]
ben rappresentata da figura 2.6. Possiamo scrivere quindi il flusso entrante
al drain come [9]
aD = a S ts tc
(2.19)
dove ts è il coefficiente di trasmissione tra il source e il virtual source, t c
il coefficiente di trasmissione nel canale, a S il flusso uscente dal source. Al
virtual source possiamo scrivere la densità di carica come [9]
n(0, y) =
ts aS + r c ts aS
ts aS (1 + rc )
a+ + a −
=
=
vth
vth
vth
(2.20)
dove si può distinguere un flusso di carica positivo che riesce a passare e
ad arrivare al drain e un flusso di carica negativo che subisce scattering e
torna indietro. Ricavando ts da (2.20) e inserendolo in (2.19), tenendo poi
presente che tc = 1 − rc , si ricava
aD = n (0, y) vth
1 − rc
1 + rc
(2.21)
dove n (0, y) è la densità di carica presente in corrispondenza del virtual
source. Ipotizzando di essere sopra soglia si ha
N2D =
Z
ymax
n (0, y) dy =
0
14
Cef f
(VGS − VT )
q
(2.22)
Integrando rispetto ad y la (2.21) utilizzando la (2.22) si ottiene
ID = W Cef f vth
1 − rc
(VGS − VT )
1 + rc
(2.23)
dove si può definire una velocità media della carica
< v(0) >= vth
1 − rc
1 + rc
(2.24)
Si può facilmente verificare che per un dispositivo balistico, cioè per r c che
tende a zero, la velocità media tende alla velocità termica v th
Il coefficiente di riflessione per alti campi r c = rhf = r è diverso da quello
per bassi campi ed è definito come
rhf =
1
lKT
=
λ
lKT + λ
1 + lKT
(2.25)
dove lKT è denominato KT-layer e vale:
lKT =
KT
qF (0+ )
(2.26)
mentre λ è il libero cammino medio tra due eventi di scattering a bassi campi
ed è definito come (2.27)
2µ0 Vth
(2.27)
λ=
vth
Dall’equazione (2.26) si può vedere che r dipende dal campo elettrico presente subito dopo il virtual source. Il parametro l KT si può anche definire
infatti come la distanza in cui la banda di conduzione decresce della quantità
KT . Ne deriva che tanto maggiore è il campo, ovvero tanto maggiore è la
pendenza con cui cambia la banda di conduzione, tanto più piccolo sarà il
KT-layer. Al ridursi di lKT il coefficiente di riflessione rhf tende a zero ed
il transistore tende al limite balistico.
Come illustrato in figura 2.7, lKT può essere intesa come la lunghezza
oltre la quale anche se la carica subisce un evento di scattering non è più
in grado di tornare al source. Altresı̀ è vero che se l’evento di scattering
avviene entro tale distanza è in grado di tornare al source.
2.6
Mobilità nei dispositivi decananometrici
Analogamente a quanto accade nella determinazione della corrente di saturazione per i dispositivi decananometrici vista nella sezione 2.5 anche per la
mobilità di questi dispositivi ci si aspetta un comportamento opportunatamente mediato tra la mobilità di canale lungo e quella balistica. Analogamente a quanto visto in [7, 14] utilizziamo per questo studio un approccio
15
l kT
Source
Drain
Figura 2.7: Rappresentazione del significato di l KT . In un MOSFET decananometrico lKT è definito come la distanza dal virtual source in cui il
massimo della banda di conduzione decresce di KT . Se le cariche subiscono
scattering oltre lKT dal virtual source non riescono a tornare al source. [10]
basato sulla flux theory. Analizzando la situazione in prossimità del virtual
source, come si può vedere da figura 2.8 saremo di fronte a due flussi, uno
positivo, dal source verso il drain e l’altro negativo, dal drain verso il source.
F (0)+ = N2D vth = 1 (S)
2
F (0)−
bal = N2D vth = 1 (D)
2
F (0)− = F (0)+ r(S) + F (0)−
bal (1 − r(D)) = N2D vth = 1 (S)r(S)
2
+N2D vth = 1 (D)(1 − r(D))
2
(2.28)
In queste espressioni è possibile usare la velocità termica v th essendo il punto
del source virtuale all’equilibrio termico. Con F (0) + si indica appunto il
flusso positivo, con F (0)−
bal si indica il flusso che inciderebbe al source se non
ci fossero eventi di scattering tra drain e source. Con F (0) − si indica il totale
flusso negativo, ovvero la composizione di ciò che torna indietro del flusso
positivo dovuto allo scattering nel canale e ciò che arriva del flusso balistico
proveniente dal drain, al netto dello scattering nel canale. N 2D è la densità di
inversione definita in equazione (2.10). Nelle (2.28) inoltre si sono abbreviati
nella scrittura gli integrali di Fermi-Dirac con = 1 (S) = = 1 ((EF − EC )/KT )
2
2
e = 1 (D) = = 1 ((EF −EC −qVDS )/KT ). Infine r(S) e r(D) sono i coefficienti
2
2
16
−
F(0)bal r(D)
low field conditions:
−
F(0) bal
+
Fx = 1 kV/cm
F(0) r(S)
+
EC
F(0)
Source
Drain
Figura 2.8: Rappresentazione dell’andamento dei flussi di eq. 2.28 in
prossimità del virtual source. Si può distinguere F (0) + ovvero il flusso che
parte dal virtual source, la porzione di esso che torna indietro a causa del coefficiente di riflessione al source r(S), F (0) −
bal ovvero il flusso che inciderebbe
al source proveniente dal drain in assenza di scattering e la parte di esso che
invece torna indietro a causa del coefficiente di riflessione al drain r(D).
di riflessione generalizzati rispettivamente dal source e dal drain verso il
canale. Dalla somma dei flussi si può quindi ottenere la corrente come
ID
W
= qF + (0) − qF − (0)
= qN2D vth = 1 (S)(1 − r(S)) − qN2D vth = 1 (D)(1 − r(D)) (2.29)
2
2
Analogamente si può ottenere l’espressione della carica come la somma dei
due contributi di flusso
n(0)+ =
n(0)− =
F (0)+
= N2D =0 (S)
+
vth
= 1 (S)=0 (D)
F (0)−
2
=
N
r(S) + N2D =0 (D)[1 − r(D)]
2D
−
= 1 (D)
vth
2
n(0) = n(0)+ + n(0)− = N2D =0 (S) + N2D
+N2D =0 (D)[1 − r(D)]

= N2D =0 (S) +
= 1 (S)=0 (D)
2
= 1 (D)
2
= 1 (S)=0 (D)
2
= 1 (D)
r(S)
2

r(S) + N2D =0 (D)[1 − r(D)]
(2.30)
17
A questo punto è necessario specificare il coefficiente di riflessione. Lo studio
in mobilità si fa per definizione a campi bassi, per cui il coefficiente di
riflessione in questo caso può essere definito come:
r(S) =
L
L+
L
r(D) =
2µ0 VT H =1 (S)
vth
= 1 (S)
L+
2
2µ0 VT H =1 (D)
vth
= 1 (D)
(2.31)
2
dove VT H = KT /q è la tensione termica, L la lunghezza di canale e 2µ 0 VT H /vth =
λ il libero cammino medio tra un evento di scattering e il successivo. Sostituendo questa nell’ultima delle (2.30) si ottiene

n(0) = N2D =0 (S) +

= 1 (S)=0 (D)
= 1 (D)
+N2D =0 (D) 1 −

= N2D
2
L
L+
2µ0 VT H =1 (D)
vth
= 1 (D)
2
h





i
Lvth = 1 (S) =0 (S)= 1 (D) + =0 (D)= 1 (S) + 2µ0 VT H =0 (S)=1 (S)= 1 (D)
2
2
2
h
= 1 (D) Lvth = 1 (S) + 2µ0 VT H =1 (S)
2
+
2µ0 VT H =1 (S)
vth
= 1 (S)
L+
2

"
L
2

2µ0 VT H =1 (D)=0 (D)
Lvth = 1 (D) + 2µ0 VT H =1 (D)
2
#
2
2
i
(2.32)
La mobilità apparente di un dispositivo è definita come
µapp
gDS L =
qnW V
(2.33)
DS →0
dove gDS /W = (1/W )∂ID /∂VDS . Derivando quindi (2.29) si trova
∂= 1 (D)
∂r(D)
1 ∂ID
2
= −qN2D vth [1 − r(D)]
+ qN2D vth = 1
2 ∂VDS
W ∂VDS
∂VDS
(2.34)
Sfruttando la proprietà delle funzioni di Fermi [35]
=j−1 (D)
∂=j (D)
=−
∂VDS
VT H
(2.35)
si trova innanzitutto la derivata del coefficiente di riflessione
∂r(D)
∂VDS
=
=

∂ 

∂VDS L +
−L
L+
L
2µ0 VT H =1 (D)
vth
= 1 (D)
2



2µ0 VT H −=1 (D) ∂= 21 (D)
2
vth
= 1 (D)2 ∂VDS
=1 (D)
2µ0 VT H
vth
= 1 (D)
2
18
"
2
1 ∂=1 (D)
+
= 1 (D) ∂VDS
2
=
#
2µ0 Lvth =1 (D)=− 1 (D) − =0 (D)= 1 (D)
2
2
Lvth = 1 (D) + 2µ0 VT H =1 (D)
2
2
(2.36)
Sostituendo ora (2.36) nella (2.34) si ottiene
1 ∂ID
W ∂VDS
2qN2D vth =− 1 (D)µ0 VT H =1 (D)
2
=
VT H vth L= 1 (D) + 2µ0 VT H =1 (D)
2
h
2qN2D vth = 1 (D)VT H vth Lµ0 =0 (D)= 1 (D) − =1 (D)=− 1 (D)
2
+
2
2
VT H vth L= 1 (D) + 2µ0 VT H =1 (D)
= 2qN2D µ0 vth
"
2
Lvth = 1 (D)=− 1 (D)=1 (D) + 2µ0 VT H =− 1 (D)=1 (D)2
2
2
2
2
vth L= 1 (D) + 2µ0 VT H =1 (D)
2
vth L= 1 (D)2 =1 (D)=− 1 (D)
+
2
i
2
vth L= 1 (D) + 2µ0 VT H =1 (D)
2
2
#
2
(2.37)
Sostituendo ora (2.37) e (2.32) nella (2.33) si trova
µapp =
gDS L
qn
2qLN2D µ0 vth
=
qN2D


Lvth = 1 (D)= 1 (D)=1 (D)+2µ0 VT H = 1 (D)=1 (D)2 +vth L= 1 (D)2 =0 (D)−vth L= 1 (D)=0 (D)= 1 (D)
−
−
−
2
2
2
2
2
2
2
vth L= 1 (D)+2µ0 VT H =1 (D)
2
h
i
Lvth = 1 (S) =0 (S)= 1 (D)+=0 (D)= 1 (S) +2µ0 VT H =0 (S)=1 (S)= 1 (D)
2
2
2
2
+
h
= 1 (D) Lvth = 1 (S)+2µ0 VT H =1 (S)
2
2
i
2µ0 VT H =1 (D)=0 (D)
Lvth = 1 (D)+2µ0 VT H =1 (D)
2
NUM
N umN U M
=
NUM
DEN
N umN U M
DenN U M
= 2Lµ0 vth Lvth = 1 (D)=− 1 (D)=1 (D) + 2µ0 VT H =− 1 (D)=1 (D)2 +
2
2
2
+vth L= 1 (D)2 =0 (D) − vth L= 1 (D)=0 (D)=− 1 (D)
!
2
2
19

(2.38)
che può essere riscritta nella forma:
µapp =

2
DenN U M
DEN
N umDEN
=
=
=
vth L=− 1 (D) + 2µ0 VT H =0 (D)
2
N umDEN
DenDEN
"
2
Lvth = 1 (S) =0 (S)= 1 (D) + =0 (D)= 1 (S)
2
2
2
+2µ0 VT H =0 (S)=1 (S)= 1 (D)
2
#
Lvth = 1 (D) + 2µ0 VT H =1 (D)
2
+2µ0 VT H =1 (D)=0 (D)= 1 (D) Lvth = 1 (S) + 2µ0 VT H =1 (S)
2
DenDEN
NUM
= = 1 (D) Lvth = 1 (S) + 2µ0 VT H =1 (S)
2
2
2
Lvth = 1 (D) + 2µ0 VT H =1 (D)
2
= 2µ0 vth = 1 (D) Lvth = 1 (S) + 2µ0 VT H =1 (S)
2
2
Lvth = 1 (D)=− 1 (D)=1 (D) + 2µ0 VT H =− 1 (D)=1 (D)2
2
2
2
2
+vth L= 1 (D) =0 (D) − vth L= 1 (D)=0 (D)=− 1 (D)
2
DEN
=
2
2
vth L=− 1 (D) + 2µ0 VT H =0 (D)
2
!
"
Lvth = 1 (S) =0 (S)= 1 (D)
2
2
+=0 (D)= 1 (S) + 2µ0 VT H =0 (S)=1 (S)= 1 (D)
2
!
2
!
Lvth = 1 (D) + 2µ0 VT H =1 (D) + 2µ0 VT H =1 (D)=0 (D)= 1 (D)
2
Lvth = 1 (S) + 2µ0 VT H =1 (S)
2
2
#
(2.39)
L’espressione (2.39) è di validità generale fin quando vale (2.31), ovvero fino
a quando siamo a bassi campi longitudinali. Per completare la (2.33) è ora
necessario valutare il limite per V DS → 0. In questo caso gli integrali di
Fermi-Dirac del source e del drain sono uguali:
=− 1 (D) = =− 1 (S) = =− 1
2
2
2
= 1 (D) = = 1 (S) = = 1
2
2
2
=0 (D) = =0 (S) = =0
=1 (D) = =1 (S) = =1
(2.40)
e quindi
lim µapp =
VDS →0
µ0 vth L
=0
2µ0 VT H =− 1 =21
2
+ vth
L=2 =
Lvth = 1 + 2µ0 VT H =1
2
20
1
2
2
0
(2.41)
L’equazione 2.41 esprime la mobilità apparente di un dispositivo decananometrico di qualsiasi lunghezza. Il modello è robusto in quanto è possibile riottenere la mobilità di canale lungo facendo tendere il dispositivo a lunghezze
infinite
=0
L→∞ µ0 vth L
lim
VDS →0
Lvth = 1 + 2µ0 VT H =1
2
2
2µ0 VT H =− 1 =21 + vth L=21 =0
2
=
2
=0 (Lvth )
2
µ0 =0 (Lvth )
=2
1
2
2
=
=2
1
2
1
µ0
(2.42)
nonchè la mobilità balistica per unità di lunghezza per un dispositivo infinitamente corto
L
lim
VDS →0 L→0 µapp
=0
=
lim
VDS →0 L→0 µ0 vth
=
=0 4µ20 VT2H =1
Lvth = 1 + 2µ0 VT H =1
2
2
2µ0 VT H =− 1 =21 + vth L=21 =0
µ0 vth 2µ0 VT H =− 1 =21
2
2
=
2
=0 2VT H
=0
=
vth =− 1
µBAL,L =− 1
2
2
(2.43)
dove
vth
(2.44)
2VT H
è la mobilità balistica per unità di lunghezza. Vediamo ora cosa accade nel
caso di gas elettronico non degenere per dispositivi di generica lunghezza
L. Nel caso non degere il rapporti tra gli integrali di Fermi-Dirac, per ogni
grado vale
=α
(2.45)
→ 1
=β
∀α,β
µBAL,L =
ed è quindi possibile semplificare la (2.41) come
1
µapp
=0 =21
=
(Lvth + 2µ0 VT H )2
Lvth + 2µ0 VT H
=
3
µ0 vth L
µ0 vth L= 1 Lvth + 2µ0 VT H
=
2VT H
1
1
1
+
+
=
µ0
vth L
µ0 µBAL,L L
2
2
(2.46)
Dall’equazione (2.46) si evince che la mobilità apparente di un dispositivo
decananometrico si comporta come il parallelo di due resistenze dove le
due resistenze sono la mobilità di canale lungo µ 0 e la mobilità balistica
µBAL,L L. Il modello viene riassunto in figura 2.9 tramite analogia circuitale.
21
µapp
µBAL,L. L
µ0
Figura 2.9: Analogia circuitale per la mobilità apparente.
Nel caso degenere le cose dal punto di vista analitico si complicano e a rigore
il modello parallelo non è più valido. Infatti la (2.40) non è semplificabile.
Facendo degli opportuni raccoglimenti è però possibile mettere in evidenza
la dipendenza da L riscrivendo:
1
µapp
=
=0
µBAL,L L=− 1
2

 1
= 
µ0
+
1
L
µBAL,L L = 21
1+
µ0
=1
1
µBAL,L
=− 1
2
=0


!





 coef fnon
1+
1+
µBAL,L L = 21
µ0
=1
=21 =0
µBAL,L
2
µ0 L =21 =
1
−2






(2.47)
lin
dove
coef fnon
lin



=


1+
1+
µBAL,L L = 21
µ0
=1
=21 =0
µBAL,L
2
µ0 L =21 = 1
−
2
!
1+

2




µBAL,L L =− 12 
µ0
(2.48)
=0
Si esamina quindi questo coefficiente per vedere la deviazione che esso
produce rispetto al modello parallelo. In figura 2.10 si può notare come tale
coefficiente abbia piccole deviazioni rispetto all’unità. Esso infatti è tanto
più forte tanto più degenerazione è presente.
Anche in casi estremi, con ηF = 10, valori non riscontrabili in dispositivi reali, il discostamento dalla linearità dell’inverso della mobilità apparente, non supera il 2%. Pertanto è possibile dedurne che nel caso degenere
possiamo introdurre la il modello parallelo a patto di tenere conto della
degenerazione con il termine =− 1 (ηF )/=0 (ηF ).
2
22
Non Linearity Coefficient
1
coeffnon lin [ ]
0.995
0.99
0.985
0.98
0
0.02
0.04
−1
−1
L [nm ]
0.06
ηF=−6
ηF=−2
ηF=2
ηF=2
ηF=6
ηF=10
0.08
0.1
Figura 2.10: Andamento del coefficiente di eq. (2.48) al variare dell’inverso
della lunghezza di canale per diversi valori di η F (dall’alto al basso -6 -2 2 6
10)
2.7
Estrazione sperimentale del coefficiente di riflessione
Il rapporto tra la il libero cammino medio λ e la lunghezza l KT , detta KTlayer, è un parametro fondamentale nello studio dei dispositivi decananometrici in quanto da esso si può ricavare il coefficiente di riflessione
r=
1
λ
1 + lKT
(2.49)
Con il metodo descritto in questa sezione, tramite delle misure della corrente
di saturazione di un dispositivo a diverse temperature, è possibile ricavare
il suo rapporto λ/lKT e quindi il coefficiente di riflessione r. Si riporta,
analogamente a quanto ricavato nella sezione 2.5, l’espressione della corrente
espressa in funzione del rapporto λ/l KT .
ID = W QIN V vth
= W QIN V vth
23
1−r
1+r
λ
lKT
2+
λ
lKT
(2.50)
dove QIN V = qN2D è la densità di carica di inversione presente al virtual
source e vth la velocità di iniezione in tale punto, che corrisponde alla velocità
termica. Definendo α come il rapporto incrementale della corrente rispetto
alla temperatura, normalizzato alla corrente a T 0 = 300K,
α=
∆ID
ID0 ∆T
(2.51)
e ipotizzando le seguenti dipendenze dalla temperatura delle varie componenti che formano la corrente
µ0 ∝ T −1.5
vth ∝ T 0.5
l ∝ T1
(2.52)
si può arrivare ad esprimere il rapporto incrementale normalizzato α come
[25]


1
4
η
1

−
α= −
λ
0
2 2+ l
T0 VGS − VT0
KT
(2.53)
0
dove λ0 /lKT0 è il rapporto λ/lKT a T0 = 300K e η è il coefficiente di temperatura della tensione di soglia vicino all’equilibrio. La semplice espressione
della densità di carica di inversione Q IN V = qN2D = Cef f (VGS − VT ) è stata usata per ricavare l’equazione (2.53). Da qui, secondo il metodo proposto
in [26], si può esprimere il rapporto λ 0 /lKT0 come
λ0
lKT0
=
4
0.5 − α +
η
VG −VT0
T0
−2
(2.54)
Siamo quindi in grado di determinare il rapporto λ 0 /lKT0 conoscendo α e
η/(VGS − VT ). Ricavare poi il coefficiente di riflessione è immediato tramite
l’equazione 2.49. L’intero metodo di estrazione è illustroato graficamente in
figura 2.11.
2.7.1
Generalizzazione del metodo di estrazione
L’espressione (2.54) ha il limite di essere valida solo se sono rispettate le
2.52. Quando esse non sono più valide si possono avere degli errori consistenti nel calcolo del rapporto λ/lKT . La dipendenza dalla temperatura della
mobilità di canale lungo ad esempio può avere delle variazioni quando l’effetto dello scattering con l’interfaccia ossido-silicio diventa preponderante, cosa
comune nei MOS di ultima generazione. É stato dimostrato inoltre, che la
dipendenza del KT-layer dalla temperatura non è semplicemente lineare ma
ha una dipendenza [14]
lKT = L β
KT
q
VDS
24
!γlKT
(2.55)
α=∆ I D / (∆T I D )
λ0
l KT 0
η/(VGS−VT )=−∆ Q INV /(∆ T Q INV )
=
4
0.5−( α − η/( VGS−VT) )
r=
−2
1
1 + λ 0/ l KT 0
Figura 2.11: Riassunto grafico del metodo utilizzato per l’estrazione del
rapporto λ0 /lKT0 .
dove γlKT ≈ 0.7. É interessante perciò ricavare il metodo generalizzando le
dipendenze dalla temperatura.
µ 0 ∝ T γµ 0
vth ∝ T γvth
lKT
∝ T γlKT
(2.56)
Dalle (2.56) si può ricavare la dipendenza dalla temperatura del libero
cammino medio λ come
VT H µ0
λ∝
∝ T (1+γµ0 −γvth ) = T γλ
(2.57)
vth
Per trovare l’espressione del rapporto incrementale di eq. (2.51) si va a
valutare la derivata rispetto alla temperatura dell’espressione della corrente
di eq. (2.50) ovvero
1 ∂ID
W ∂T
h
∂vth
T
= −Cef f vth ∂V
∂T + Cef f (VGS − VT ) ∂T
+Cef f (VGS −
∂
VT ) vth ∂T
λ
lKT
2+ l λ
KT
i
λ
lkT
2+ l λ
KT
+
(2.58)
Tenendo presente le (2.56) è possibile trovare le derivate rispetto alla temperatura presenti nell’equazione (2.58). Infatti partendo dalle derivate
T γλ
∂λ
λ
λ =
λ0 =⇒
= γλ
T
∂T
T
0 γl
KT
∂lKT
lKT
T
lKT0 =⇒
= γlKT
lKT =
T
∂T
T
0 γv
th
T
∂vth
vth
vth0 =⇒
= γvth
vth =
T0
∂T
T
25
(2.59)
si può ricavare il valore della derivata
∂
∂T
λ
lKT
1 ∂λ
λ ∂lKT
− 2
lKT ∂T
lKT ∂T
γlKT λ lKT
γλ λ
− 2
lKT T
lKT T
λ
(γλ − γlKT )
lKT · T
=
=
=
(2.60)
con la quale è possibile esprimere il termine presente alla fine dell’equazione
2.58)
∂
∂T
λ
lKT
2+
λ
lKT
!
=
=
=
=
∂
1
λ ∂T
2 + lKT
λ
lKT
lKT
2+
λ
lKT
2
T
λ
lKT
−
2+
2+
λ
lKT
λ
lKT
λ
∂
2
∂T
lKT
2
2+
λ
lKT
1
2+
λ
lKT
2
γλ − γlKT
T
(γλ − γlKT )
λ
lKT
2 (γλ − γlKT )
1
(γλ − γlKT ) −
λ
2 + lKT
λ
2 lKT
λ
2+
T
λ
lKT
!
(2.61)
Riprendendo quindi la (2.58) è possibile arrivare all’espressione della derivata della corrente rispetto alla temperatura
1 ∂ID
= Cef f (VGS − VT ) vth
W ∂T
λ
lKT
2+
λ
lKT
!"
−η
γv
2 (γλ − γlKT )
+ th + VGS − VT
T
2+ λ T
lKT
#
(2.62)
Come si può vedere il fattore fuori dalle parentesi quadre della (2.58) altro
non è che l’espressione della corrente vista in equazione (2.50). Questo rende
immediato scrivere il rapporto incrementale α calcolato in T 0 come
∆ID
α=
∆T · ID0
=


2 (γλ − γlKT ) 
1 
η
γvth +
−
λ
0
T0
VGS − VT0
2 + lKT
0
=


2 (1 + γµ0 − γvth − γlKT ) 
1 
η
γvth +
−
λ
0
T0
VGS − VT0
2+ l
KT0
(2.63)
Essendo il rapporto λ0 /lKT0 l’incognita del problema, possiamo esplicitarne
l’espressione
λ0
−2 (1 + γµ0 − γvth − γlKT )
=
−2
(2.64)
η
lKT0
γv − α +
T0
VGS −VT0
th
26
Si può facilmente verificare che sostituendo le dipendenze delle (2.52) in
(2.64) ovvero ponendo γµ0 = −1.5, γvth = 0.5 e γlKT = 1 si può riottenere
l’equazione (2.54). Se esprimiamo Q IN V come:
QIN V = Cef f (VGS − VT )
(2.65)
allora, data la definizione di η:
η=
∆VT
∂VT
=
∂T
∆T
(2.66)
si ha
∆QIN V
∆T
∆QIN V
∆T · QIN V
∆VT
η
∆VT
1
Cef f ; −
=−
∆T
VGS − VT
∆T VGS − VT
1
1
∆QIN V
∆VT
=−
(2.67)
∆T Cef f (VGS − VT )
∆T VGS − VT
= −
=
e quindi:
∆QIN V
η
=−
VGS − VT
∆T · QIN V
(2.68)
Tramite la (2.68) è possibile riscrivere la (2.64) come
λ0
lKT0
=
−2 (1 + γµ0 − γvth − γlKT )
γvth −
∆ID
∆T ·ID0
27
−
∆QIN V
∆T ·QIN V0
T0
−2
(2.69)
28
Capitolo 3
Simulatore Monte Carlo
In questo capitolo, partendo da una breve trattazione dell’equazione del
trasporto di Boltzmann, viene introdotto il metodo Monte Carlo. Si passa
in seguito ad una breve descrizione del simulatore utilizzato.
3.1
L’equazione del trasporto di Boltzman
La risoluzione completa del funzionamento di un dispositivo corrisponde a
sapere, per ogni particella presente, la posizione e la sua quantità di moto.
Se la particella si comporta secondo la fisica classica, essa deve sottostare
alle equazioni di Newton che sono
dpi
= (−q)F + R(r, p, t)
dt
dri
= vi (t)
dt
(3.1)
(3.2)
dove pi (t) è la quantità di moto, r la posizione e R(r, p, t) è la forza casuale
dovuta a impurità o vibrazioni reticolari.
La soluzione del problema per ogni portatore è tanto impraticabile quanto poco utile, risulta infatti più conveniente descrivere la probabilità con cui
possiamo trovare una particella in un determinato punto, con una certa
quantità di moto ad un certo istante. Questa probabilità prende il nome di
funzione di distribuzione f (r, p, t). La funzione di distribuzione altro non
è che la soluzione dell’equazione di Boltzmann e può essere utilizzata per
ottenere varie grandezze macroscopiche come la distribuzione di carica e la
corrente. All’equilibrio, situazione in cui il gas elettronico ha un moto browniano a velocità media nulla, ovvero in cui lo scambio di energia tra reticolo
e gas elettronico si equipara in entrambi i versi, la distribuzione è la funzione
di Fermi-Dirac
1
f0 (p) =
(3.3)
[E
(
r
,
1 + e C p)−EF ]/KTL
29
dove EF è il livello di Fermi, TL è la temperatura del reticolo e
EC (r, p) = EC0 (r) + E(p)
(3.4)
dove EC0 (r) è la somma delle energie potenziali delle cariche, e E(p) è la
somma delle energie cinetiche. Se assumiamo le bande di energia sferiche e
paraboliche, ovvero nel caso in cui valga E(p) = p 2 /2m∗ , per un semiconduttore non degenere la (3.3) può essere ben approssimata con una funzione
Maxwelliana
2
∗
f0 (p) = e[EF −EC (r,p)] × e−p /2m KTL
(3.5)
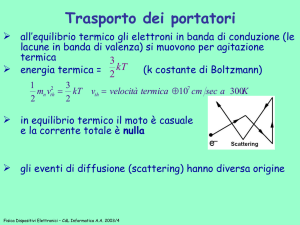
Da figura 3.1 si può vedere come la velocità media della distribuzione sia
nulla; condizione tipica, appunto, di un moto browniano.
f(p)
p
Figura 3.1: Andamento della distribuzione Maxwelliana f 0
Nel caso di non equilibrio la funzione di distribuzione non è più esprimibile tramite l’equazione (3.5). Per molti casi è possibile approssimare la
distribuzione come una maxwelliana traslata, ovvero come una maxwelliana
che abbia velocità media non più nulla. Comunque queste approssimazioni
possono valere per piccoli discostamenti dall’equilibrio. Quando siamo molto
fuori dall’equilibrio, ovvero in casi in cui la temperatura del reticolo cristallino è molto minore della temperatura delle cariche a causa di alti campi, la
forma delle distribuzioni non è più approssimabile tramite delle maxwelliane
e si rende necessaria la soluzione completa dell’equazione del trasporto di
Boltzmann.
Come detto la funzione di distribuzione ci dà la probabilità di trovare
in un determinato istante una particella in un determinato punto r con
30
una determinata quantità di moto p. L’equazione di Boltzmann descrive il
modo in cui la funzione di distribuzione cambia nel tempo e nello spazio.
L’equazione di Boltzmann è di fatto un’equazione di continuità nello spazio
delle fasi che ha sei dimensioni: tre per la posizione e tre per la quantità
di moto (vedi figura 3.2). Considerando la posizione e la quantità di moto
Figura 3.2: Raffigurazione della cella infinitesima nello spazio (r, p). [4]
monodimensionale, per semplicità, si prende in esame un infinitesimo di
spazio δS = δpδr. In un infinitesimo temporale δt si va a vedere cosa succede.
Come si può vedere anche in figura 3.2 abbiamo un flusso entrante ed uno
uscente in entrambe le dimensioni. Inoltre c’è un termine di generazione
dovuto allo scattering. La conservazione della carica richiede dunque
δf δrδp = [f (r) − f (r + δr)] vδtδp + [f (p) − f (p + δp)] F orce δtδr
∂f (3.6)
+ δtδrδp
∂t coll
dove Force = ∂p/∂t è la forza applicata e v = ∂r/∂t è la velocità. La (3.6)
può essere riscritta raccogliendo il termine δrδpδt e facendo tendere a zero
i tre infinitesimi come
∂f
∂f
∂f
∂f .
+v
+ Force
=
∂t
∂r
∂p
∂t coll
31
(3.7)
Questa altro non è che l’equazione di Boltzmann monodimensionale, che in
sei dimensioni diventa
∂f ∂f
+ v · ∇r f + Force · ∇p f =
∂t
∂t coll
(3.8)
dove v è la velocità delle particelle che in generale vale v = ∇ p E(p) (che si
semplifica in v = p/m∗ solo per una struttura a bande parabolica ovvero per
E(p) = p2 /(2m∗ )). Nella (3.8) si può distinguere il termini di generazionericombinazione dovuta agli eventi di scattering. A rigore esso è espresso
tramite la
X
X
∂f =
f (p’) [1 − f (p)] S(p’, p) −
f (p) [1 − f (p’)] S(p, p’) (3.9)
∂t coll
p’
p’
dove il termine [1 − f (p)] indica la probabilità che lo stato p sia occupato.
Per semiconduttori non degeneri tale probabilità è prossima all’unità essendo
f (p) molto piccola rispetto ad uno. Pertanto la (3.9) può essere riscritta
come
X
X
∂f f (p)S(p, p’)
(3.10)
f (p’)S(p’, p) −
=
∂t coll
p’
p’
Si può dimostrare [4] che per bassi campi applicati il termine di generazionericombinazione può essere approssimato mediante il metodo del tempo si
rilassamento come
(f − f0 )
∂f =
(3.11)
∂t coll
τf
dove τf è il tempo caratteristico che descrive in che modo la funzione di
distribuzione tende a tornare alla Maxwelliana di equilibrio f 0 .
3.2
Simulazioni Monte Carlo
Nella sezione 3.1 è stata introdotta l’equazione del trasporto di Boltzmann
ovvero la BTE. La sua soluzione però è molto difficile dal punto di vista
matematico. Una soluzione numerica può essere ottenuta simulando il comportamento delle particelle responsabili del flusso di carica, cioè studiando
le traiettorie di ognuna di esse all’interno del dispositivo in esame. Queste
traiettorie sono il risultato del campo elettrico applicato e degli eventi di
scattering. Questo metodo di simulazione numerica prende il nome di tecnica Monte Carlo. Se il numero di traiettorie simulate e quindi di particelle è
abbastanza elevato si riesce a rappresentare il comportamento delle cariche
all’interno di un dispositivo reale. Grazie a questo tipo di simulazioni si
sono costruite la maggior parte delle conoscenze riguardo il trasporto ad alti
campi elettrici.
32
3.2.1
Simulazione del moto di una particella
Il comportamento di una particella si può riassumere in due distinte fasi,
quella dello scattering e quella del volo libero tra due eventi di scattering
successivi. In figura 3.3(a) è rappresentato il tipico percorso di una particella. Come si può vedere il volo libero è interrotto dagli eventi di scattering,
che vengono considerati istantanei.
Figura 3.3: (a)Rappresentazione della traiettoria nel piano (x, z) con campo
elettrico presente in direzione −x. (b)Andamento della quantità di moto
lungo x. [4]
Ogni evento di scattering cambia istantaneamente la quantità di moto
della particella ma non la sua posizione, vedi figura 3.3(b). Infatti, se il
cambiamento di posizione durante una collisione è ∆r = v∆t e ipotizziamo
la collisione istantanea (∆t = 0), va da sè che il cambiamento di posizione
è nullo. La frequenza di questi eventi è data dallo scattering rate, che altro
non è che una frequenza dipendente dall’energia ovvero dalla quantità di
moto. Esso dipende dai vari meccanismi di scattering di cui si tiene conto e
33
si può scrivere come
Γ(p) =
nsc
X
i=1
1
τi (p)
(3.12)
dove τi (p)−1 è lo scattering rate dei nsc meccanismi di scattering, che dipendono a loro volta dall’energia ovvero dalla quantità di moto p. In figura
3.4(a) viene riportato un esempio dell’andamento dello scattering rate al
variare dell’energia E; in figura 3.4(b), i contributi dei vari meccanismi di
scattering. In questo caso ne vengono considerati quattro. Durante la fase
Figura 3.4: (a) Andamento dello scattering rate al variare dell’energia. (b)
Andamento dei vari contributi allo scattering rate al variare dell’energia:
1 = fononi acustici, 2 = assorbimento fononi ottici, 3 = emissione fononi
ottici, 4 = impurità ionizzate [4]
di volo libero il momento della particella cambia secondo l’equazione
Force =
∂p
= (−q) F
∂t
(3.13)
e la sua posizione secondo
r(t) = r(0) +
Z
t
v(u)du
(3.14)
0
Supponendo ad esempio che la particella si muova in presenza del solo campo Fx in direzione x. Le (3.13) e (3.14) possono essere riscritte per ogni
componente come
px (t) = px (0) + (−q)Fx t
py (t) = py (0)
pz (t) = pz (0)
px (0)
(−q)Fx 2
E(t) − E(0)
t+
t = x(0) +
m∗
2m∗
(−q)Fx
py (0)
y(t) = y(0) +
t
m∗
pz (0)
z(t) = z(0) +
t
m∗
(3.15)
x(t) = x(0) +
(3.16)
dove si sono ipotizzate delle bande paraboliche di energia con E(t) = p(t) 2 /(2m∗ ),
E(t) = p(0)2 /(2m∗ ) ed un campo elettrico costante lungo il volo libero.
34
Per simulare un volo libero ed un successivo evento di scattering si genera
una successione di quattro numeri casuali. Il primo di essi determina la
durata del volo, il secondo determina il meccanismo di scattering tra quelli
considerati e gli ultimi due servono per la determinazione della direzione del
volo dopo lo scattering. L’algoritmo viene schematizzato in figura 3.5.
Figura 3.5: Algoritmo Monte Carlo.
Per quanto riguarda lo scattering rate Γ(p) dalla (3.12) non si deduce
nessuna dipendenza dal tempo. Si vede una dipendenza dalla sola energia, ma la (3.13) descrive l’incremento di quantità di moto nel tempo. Ne
deriva che anche lo scattering rate è dipendente dal tempo. Questa dipendenza viene tenuta in considerazione mediante un artificio, ovvero mediante
il cosiddetto self scattering. In breve, si massimizza lo scattering rate e lo si
rende costante in energia ponendo
Γ(p) = Γ0 =
nsc
X
i=1
1
τi (p)
(3.17)
Ad ogni evento di scattering, che ora avverrà mediamente più frequentemente
rispetto a quanto previsto dagli scattering rate di equazione (3.12), viene
estratto un numero casuale. Se tale numero corrisponde al self-scattering
non avremo alcun evento di scattering, cioè si è trattato di uno scattering
fittizio che non cambierà la quantità di moto della nostra particella. In
figura 3.6 viene schematizzato tale meccanismo.
Si può vedere che la probabilità di avere un self-scattering decresce nel
tempo ovvero nell’energia in quanto vale
1
τnsc +1
3.3
= Γself (p) = Γ0 − Γ(p)
(3.18)
Quantizzazione verticale in strutture MOS
Denominiamo con direzione verticale la direzione ortogonale allo strato di ossido di silicio. Nei dispositivi nMOS, per ottenere lo strato invertito di carica
necessario al normale funzionamento è indispensabile applicare al terminale
di gate una tensione superiore alla tensione si soglia. In tale circostanza,
nei dispositivi odierni in cui lo scaling è molto spinto, si forma una buca di
potenziale molto stretta che produce fenomeni quantistici. Quando la buca
di potenziale diventa sufficientemente stretta, il gas diventa 2DEG in quanto i portatori sono liberi di muoversi nel piano del trasporto ma confinati in
direzione verticale. In questo caso quindi è necessario risolvere l’equazione
35
Figura 3.6: Rappresentazione del self-scattering. Ad ogni evento di scattering si estrae un numero casuale e se tale numero corrisponde al self-scattering
lo scattering non avviene, ma sarà solo fittizio, senza cambiare lo stato della
particella. [4]
di Schrödinger
h̄2
−
2
1 ∂ξ(r)
1 ∂ξ(r)
1 ∂ξ(r)
+ ∗
+ ∗
∗
2
2
mx ∂x
my ∂y
mz ∂z 2
!
+ U (y)ξ(r) = (E − EC ) ξ(r)
(3.19)
dove ξ(r) = ξ(x, y, z) è la funzione di inviluppo e nel caso in questione si
può scrivere come
ξ(x, y, z) = ψ(y)ei(kx x+kz z)
(3.20)
L’equazione (3.20) riassume la natura 2DEG del gas elettronico in quanto si può distinguere una parte libera nel piano (x,z) con un comportamento di onda piana e una parte che segue l’equazione di Schrödinger
monodimensionale
−
h̄2 ∂ 2 ψ(y)
+ U (y)ψ(y) = E⊥ ψ(y)
2m∗y ∂y 2
(3.21)
Come si può vedere, per ottenere l’equazione (3.21), l’energia è stata divisa
in due contributi: la E// parallela al piano (x,z) e l’autovalore E ⊥ prodotto
dal confinamento verticale:
E = E⊥ + E//
h̄2
= E⊥ +
2
kz2
kx2
+
m∗x m∗z
!
(3.22)
Il contributo E// è continuo essendo l’energia di un gas libero. Il contributo
E⊥ invece è discretizzato analogamente da come accadrebbe per una buca di
36
potenziale rettangolare di larghezza L con potenziale infinito, i cui autovalori
sono noti in modo analitico e valgono:
E⊥,rect,n =
h2 n2
h̄2 2
k
=
y,n
2m∗y
8m∗y L2
(3.23)
Andando a vedere la struttura della banda di conduzione del silicio h100i possiamo vedere che si possono distinguere due tipi di sottobande. Ci sono quelle
relative alle due valli longitudinali alla direzione di quantizzazione, indicate
con ∆2 e le quattro trasversali, indicate con ∆4. Avendo m ∗y,∆2 = 0.916m0
e m∗y,∆4 = 0.19m0 , dove m0 è la massa dell’elettrone nel vuoto, guardando
la (3.23) ci si aspetta che le sottobande corrispondenti a ∆2 abbiano energie
più basse, mentre quelle corrispondenti a ∆4 energie superiori. Le prime
bande vengono anche denominate unprimed, mentre le seconde primed.
−0.1
V [eV]
CB(y)
−0.3
Unprimed (1 subband)
Primed (2 subbands)
−0.5
−0.7
−1.0
0.0
1.0
y [nm]
2.0
3.0
4.0
Figura 3.7: Rappresentazione delle sottobande nella buca di potenziale a
forma triangolare tipica di un MOS. Si possono distinguere cinque sottobande unprimed con linea continua e cinque bande primed doppie con linea
tratteggiata.
In figura 3.7, relativa alla struttura della banda di conduzione di un
MOS nello strato di inversione, si vede infatti che la prima sottobanda è
unprimed, le seconda, a notevole distanza energetica, è primed, e la terza,
quasi attaccata alla seconda, è nuovamente unprimed.
3.4
Simulatore CoSMOS2D
Il simulatore Monte Carlo utilizzato è quello realizzato dal gruppo di microelettronica dell’Università degli studi di Udine. Si basa sullo studio del
37
comportamento delle particelle di un gas 2D. Trattare gli elettroni come un
gas 2D è necessario nei dispositivi decananometrici odierni in quanto lo strato invertito di particelle, che si viene a formare in seguito all’applicazione di
una tensione di bias al gate superiore alla tensione di soglia, è confinato in
una buca di potenziale come già trattato nella sezione 3.3. Per un dispositivo
SOI DG, ad esempio, possiamo ottenere un profilo di banda di conduzione
come quello di figura 3.8. Guardando la banda di conduzione discretizzata
Figura 3.8: Tipica struttura a bande per un dispositivo SOI DG. [33]
si nota che gli elettroni non risiedono nel fondo della banda di conduzione
ma in una delle sottobande discretizzate. Nel caso di orientazione h100i ci si
trova di fronte a due tipi di sottobande, quelle corrispondenti alle due ellissi
in direzione ŷ e quelle corrispondenti alle quattro ellissi in direzione x̂ e ẑ.
A seconda di quale sottobanda venga occupata da una particella, la massa
di quest’ultima cambierà. Il funzionamento del simulatore è schematizzato
in figura (3.9). L’idea alla base del simulatore è quella di simulare un dispositivo bidimensionale operando delle sezioni nella direzione da source a
drain. Per ognuna di queste sezioni s viene innanzitutto risolta l’equazione
di Schrödingher (3.24), per trovare localmente la struttura a bande,
!
h̄2 ∂ 2
− qφs (y) ψs,v,i = Es,v,i ψs,v,i
2m∗y ∂y 2
(3.24)
La banda discretizzata di conduzione sarà rappresentata da un set di autovalori Es,v,i e da un set di autofunzioni ψs,v,i dove v è l’indice delle valli.
Nella computazione si fa l’ipotesi semplificativa che il potenziale non sia
dipendente dal potenziale delle fette vicine in direzione x̂ e che il potenziale
sia indipendente da z (ovvero nella direzione della larghezza del dispositivo).
Con questa ipotesi prendiamo ogni fetta come se appartenesse ad un dispositivo di lunghezza infinita. Con le autofunzioni ψ s,v,i (y) e gli autovalori Es,v,i
38
Equazione di Poisson
Concentrazione
di carica n(y)
Potenziale
V(y)
Monte Carlo
Equazione di Shrodinger
Autofunzioni,
Autovalori
Φ v,i(y), E v,i
Scattering
Rates
Teoria scattering
in gas 2D
Figura 3.9:
simulatore
Schema riassuntivo dell’algoritmo di funzionamento del
vengono computati gli scattering rate per ogni sezione. Con gli scattering
rate e la soluzione dell’equazione di Schrödinger è possibile far partire la
routine Monte Carlo simulando il trasporto di un certo numero di elettroni
nel dispositivo. Essi si muovono soggetti al campo elettrico efficace
Fs,v,i = −
Es+1,v,i − Es,v,i
d
Es,v,i = −
dx
xs+1 − xs
(3.25)
dove xs è la coordinata x della sezione s. Gli scattering avvengono tra valli
e sottobande in accordo con gli scattering rate. Seguendo questo comportamento e il potenziale φ(y) la routine riesce a popolare le varie sottobande.
Dopo un transitorio iniziale, il Monte Carlo inizia a computare, ad intervalli
di tempo prefissati, la media delle popolazioni elettroniche per ogni sottobanda, per ogni valle, in ogni sezione. Queste statistiche vengono chiamate
statistiche cumulative. Con esse è possibile computare la densità elettronica
nel dispositivo come
ns (y) =
X X Ns,v,i
v
Ns
i
|ψs,v,i (y)|2
(3.26)
dove
Ns =
XX
v
Ns,v,i
(3.27)
i
è la totale carica per ogni sezione. Avendo ottenuto la distribuzione della carica n(xs , y) dove n(xs , y) = ns (y) è possibile risolvere l’equazione di
Poisson
q
∇2 φ = − [p − n + NA − ND ]
(3.28)
39
dove NA e ND sono la concentrazione dei droganti. Al fine di calcolare in
modo auto-consistente n e φ dobbiamo iterare n (k+1) che è soluzione della
routine Monte Carlo su base di φ(k) , e φ(k+1) che è la soluzione dell’equazione
di Poisson su base di n(k) ovvero
∇2 φ(k+1)
q
=−
φ(k+1) − φ(k)
−n(k) exp q
KT
!
+ NA − ND
!
(3.29)
La struttura dell’algoritmo del simulatore, come si può vedere da figura
3.9, è ciclica, funziona quindi ad iterazioni successive. Se ne deduce che
ogni simulazione avrà bisogno di un certo tempo di assestamento prima di
poter essere considerata terminata. Inoltre si dovrà partire da una soluzione
iniziale. Questo simulatore infatti è stato scritto in modo tale da riuscire
a prendere come soluzione iniziale la soluzione data dal simulatore ISEDessis. Esso è un simulatore Drift-Diffusion con implementate correzioni
quantistiche. Da esso quindi abbiamo la soluzione iniziale del potenziale,
della concentrazione di carica, dei profili di doping e della geometria del
dispositivo.
3.4.1
Meccanismi di scattering in CoSMOS
Come visto già in questo capitolo, vedi sezione 3.2.1, nell’approssimazione
di trasporto semiclassico, il movimento delle particelle consiste in voli liberi
interrotti da eventi di scattering istantantanei. All’evento di scattering corrisponde un cambiamento di vettore d’onda, di sottobanda o di valle per un
elettrone, causata dall’iterazione di questo con un potenziale di scattering.
I vari tipi di scattering implementati sono con impurezze, vibrazioni reticolari, interfaccia ossido/silicio, difetti del cristallo, altre cariche, e per ognuna
di esse c’è un potenziale di scattering. I meccanismi di scattering possono
essere classificati secondo diverse tipologie:
• Elastici o Inelastici: nel primo l’energia iniziale e finale della particella
è la stessa, nel secondo la particella perde o guadagna energia.
• Isotropo o Anisotropo: nel primo il meccanismo di scattering agisce in
modo uguale per ogni direzione del vettore d’onda, nel secondo invece
ne dipende.
• Intervalle o Intravalle: nel primo il potenziale di scattering può alterare il vettore d’onda della particella in modo tale da produrre il
cambio della valle di appartenenza. Nel secondo caso non produce un
cambio di valle.
• Itravalle Intersottobanda o Intravalle Itrasottobanda: in questo caso è
la sottobanda che può o non può essere cambiata rispettivamente.
Lo stato di una particella è caratterizzata da
40
• il suo vetore k nel piano kx − ky
• l’indice della valle in cui risiede, v
• l’indice della sottobanda, i
Quindi possiamo indicare tale stato come s(k, v, i). Una volta che abbiamo
identificato il meccanismo di scattering m e il suo potenziale di scattering
Um (r) è possibile ricavare il transition rate T R m (s, s’), che è la probabilità
per unità di tempo che l’elettrone passi istantaneamente dallo stato s allo stato s’. Per motivi computazionali, il simulatore MC non può lavorare
con i transition rate. In primo luogo procede alla determinazione dello scattering rate integrando il trasition rate per ogni stato successivo e per ogni
meccanismo di scattering.
SRm (s) =
X
T Rm (s, s’)
(3.30)
s’,m
Lo scattering rate, come si può intuire, è quindi la probabilità per unità di
tempo che un elettrone nello stato s passi in uno stato qualsiasi a causa di
un meccanismo di scattering qualsiasi. É questa la probabilità per unità di
tempo con cui si devono interrompere i voli liberi delle particelle. Quando
l’evento di scattering avviene è poi necessario individuare quale meccanismo
ha avuto luogo, anche per poi determinare lo stato finale dell’elettrone. Per
fare questo ci si serve di
SRm (s)
(3.31)
pm (s) =
SR(s)
P
P
dove SR(s) = m SRm (s) e per ovvi motivi m pm (s) = 1. Si può quindi
determinare il meccanismo di scattering dall’estrazione di un numero casuale
tra 0 e 1. Analogamente è possibile determinare la valle finale, qualora lo
scattering sia intervalle, e la sottobanda finale. Per il vettore d’onda finale la
questione è un po’ più complessa in quanto si deve imporre la conservazione
dell’energia e della quantità di moto. Il calcolo della quantità di moto finale
dipende dal tipo di meccanismo di scattering, ovvero dal fatto che esso sia
isotropo o anisotropo. Nel caso di meccanismo isotropo i vincoli sono posti
solo sul modulo del vettore d’onda, mentre la direzione finale è incorrelata
alla direzione iniziale. Contrariamente per il caso anisotropo c’è correlazione
tra le due direzioni. Tornando alla determinazione del transition rate sopra
menzionata, per la sua computazione CoSMOS procede innanzitutto alla
determinazione della matrice di scattering, ovvero ai suoi elementi. Per
ognuno di essi si può scrivere
0
0
Hs0 ,s = s |Um (r)| s =
Z
eik·r
e−ik ·r
ψv∗0 ,i0 (y) √ Um (r)ψv,i (y) √ dydr
A
A
(3.32)
dove A è l’area di normalizzazione dell’autofunzione ψ v,i (y) che è riferita
alla valle v e alla sottobanda i. Con l’ipotesi di scattering debole, ovvero
41
infrequente, è possibile applicare la Fermi’s Golden Rule per calcolare gli
scattering rates.
T Rm (s’, s) =
2
2π Hs’,s δ(Ev0 ,i0 (k’) − Ev,i (k) − ∆E)
h̄
(3.33)
dove la funzione δ proviene dall’ ipotesi di scattering debole [4]. In questo
modo T Rm è dipendente dal quadrato dell’elemento della matrice di scattering e la conservazione dell’energia è imposta all’evento di scattering.
Successivamente si va a determinare lo scattering rate dallo stato iniziale
SRm (s) =
XXZ
v0
T Rm (s, s’)dk’
(3.34)
i0
A rigore in questo passaggio, nel integrale di (3.34), si dovrebbe tenere conto
degli finali già occupati. L’integrale invece è fatto su tutti i possibili stati non
badando alla loro occupazione. La degenerazione si implementa mediante il
meccanismo di reiezione, dove lo scattering viene accettato o scartato sulla
base del confronto di un numero casuale con la probabilità di occupazione
dello stato finale. Il passo successivo alla determinazione di SR(s), e quindi
dell’evento di scattering, è la determinazione dello stato finale. I meccanismi
di scattering implementati in CoSMOS sono
• Scattering fononico
• Scattering con le asperità dell’interfaccia
• Scattering con impurezze ionizzate
• Scattering da irregolarità nello spessore t Si del silicio
Di questi sono stati utilizzati solo i primi due, di cui di seguito si dà una
breve descrizione.
Scattering fononico
Buona parte dello scattering in un semiconduttore avviene a causa delle vibrazioni del reticolo. Quando un atomo è spostato dalla sua posizione di
equilibrio nel reticolo, le forze di legame tendono a riportarlo all’origine, cosicché esso tende ad oscillare attorno a tale posizione di equilibrio. Siccome
queste onde si propagano attraverso un mezzo periodico quale è il reticolo,
hanno proprietà molto simili alle onde di Bloch. In figura 3.10 si riporta la
relazione di dispersione ω, la pulsazione, in funzione di β, il vettore d’onda,
per le onde elastiche in un semiconduttore. In relazione alle valli si possono
distinguere tre modi per le onde acustiche e tre modi per le onde ottiche; in
entrambi i casi due modi sono trasversali e uno è longitudinale. Nella figura a fianco c’è l’approssimazione che viene effettuata. Infatti per i fononi
42
ω
ω
Longitudinali
Trasversali
ω = ω0
Ottici
ω = vs β
β
Acustici
β
Figura 3.10: Relazione di dispersione per fononi. A destra è riportata
l’approssimazione utilizzata. [4]
acustici, per bassi valori di β, si effettua l’approssimazione ω(β) = v s β con
vs la velocità del suono. Tale approssimazione è buona in quanto scattering
di questo tipo comportano fononi con vettori d’onda vicini al centro della
zona di Brillouin. Per i fononi ottici invece si effettua l’approssimazione
ω(β) = ω0 .
Fononi elastici
Un elettrone che urta un fonone elastico può muoversi da una sottobanda
ad un’altra se possiede sufficiente energia da per poter superare la distanza
energetica tra le due sottobande, ma non può cambiare valle. Gli elementi
della matrice di scattering si possono esprimere come
2
D 2 KT (v,v0 )
A
2
Fi,i0
Hs’,s C = |hs’ |Uac | si| = AC
2
ul ρA
(3.35)
dove DAC è il parametro conosciuto come potenziale di deformazione acustico, K è la costante di Boltzmann, T è la temperatura del reticolo, u l è la
velocità longitudinale del suono, ρ è la densità del silicio e A è l’area di normalizzazione. Inoltre l’espressione non dipende dallo stato iniziale e finale,
eccetto per il fattore di overlap
(v,v 0 )
Fi,i0
=
Z
y1
y0
|ψi (y)|2 |ψi0 (y)|2 dy
(3.36)
dove ψi (y) è l’autofunzione della i-esima sottobanda, y 1 e y2 sono gli estremi
del nostro dispositivo in direzione verticale.
Fononi intervalle
L’interazione con un fonone intervalle non è elastica. L’elettrone infatti
43
guadagna o perde una quantità di energia pari a h̄ω ph = KTP H , dove TP H
è detta temperature del fonone e ωph frequenza angolare del fonone, a seconda che il fonone sia assorbito o emesso. Questo tipo di scattering è intervalle, ovvero l’elettrone cambia valle a seguito dell’evento di scattering. Gli
elementi della matrice di scattering sono
2 h̄
1 1
DOP
(v,v 0 )
OP 2
gv,v0 NOP (h̄ωph ) + ∓
Fi,i0
Hs0 ,s =
2ρωph A
2
(3.37)
2
dove DOP è il potenziale di deformazione ottica, N OP (h̄ωph ) è il numero di
fononi dato dalla statistica Bose-Einstein
NOP (h̄ωph) =
1
exp
h̄ωph
KT
(3.38)
−1
e gv,v0 è il numero di valli disponibili. Andando a guardare la configurazione
y
y
g−type
x
z
f−type
x
z
Figura 3.11: Rappresentazione dei due tipi di scattering intervalle. A sinistra
è raffigurato il g-type e destra l’ f-type.
delle valli, vedi figura 3.11 si possono distinguere due tipi di scattering intervalle. Infatti il salto può avvenire verso la valle speculare con la stessa
orientazione o verso una delle quattro valli con differente orientazione. Nel
primo caso si dice che siamo di fronte ad uno scattering di tipo g-type mentre
nel secondo ad un f-type.
Scattering con l’interfaccia
Consiste nello scattering dell’elettrone con l’interfaccia tra silicio ed ossido
di silicio. Questo è il principale fattore che degrada la mobilità dei dispositivi MOSFET rispetto alla mobilità del materiale bulk. Questo fenomeno è
44
tanto più forte tanto più è marcato il confinamento della carica. Il processo
di crescita dell’ossido di silicio lascia inevitabilmente una superficie irregolare e ruvida e lascia quindi uno spessore di ossido t ox irregolare. Essendo il
gate d’altro canto equipotenziale, questo fenomeno lascia delle irregolarità
nel potenziale di confinamento lungo il canale. Il risultato è che il minimo della sottobanda è irregolare e queste irregolarità producono eventi di
scattering. Il fenomeno cresce all’aumentare delle tensioni di gate, perchè
si acuisce il confinamento dei portatori. Per dispositivi di tipo SOI questo
fenomeno deve essere considerato in entrambe le interfacce. Il primo passo
per la computazione dello scattering rate è di descrivere statisticamente la
qualità dell’interfaccia. L’irregolarità è descritta da uno spettro di densità
di potenza che è la trasformata di Fourier della funzione di auto-correlazione
monodimensionale che descrive la ruvidezza dell’interfaccia nella direzione
del trasporto. I parametri che regolano questo spettro sono ∆, ovvero la media r.m.s dell’ampiezza della irregolarità di interfaccia, e Λ, ovvero la media
della sua variazione spaziale in direzione parallela all’interfaccia. Questo
spettro può essere approssimato con una funzione gaussiana:
"
−Λ2 t2
SSR (t) = πΛ ∆ exp
4
2
2
o esponenziale
SSR (t) = πΛ2 ∆2 #
(3.39)
1
1+
Λ 2 t2
2
(3.40)
3/2
dove t = kx0 − kx . Questo meccanismo è elastico, quindi ha solo l’effetto di
cambiare la direzione della particella. Inoltre esso è anisotropo, in quanto
dipende da t ovvero dalla differenza tra la componente lungo il trasporto
del vettore d’onda. Infatti lo scattering rate è computato dall’elemento di
matrice:
2
S
Hs,s0 R(q) =
h̄4

dψ  v,i (v) (v)
dy y
4my my A
int
dψv0 ,i0 dy y
2
int

SSR (q)
(t)2
(3.41)
dove (q) è la funzione dielettrica usata per lo screening, y int è il valore di y
(v)
all’interfaccia e my è la massa di quantizzazione della valle v-esima. Come
si può notare l’elemento di matrice è fortemente dipendente dalla ripidità del
potenziale all’interfaccia e dal prodotto ∆Λ e dalla derivata dell’autofunzione
all’interfaccia.
3.4.2
Modello per i contatti
Nel simulatore è possibile impostare quattro tipi di contatti, quindi quattro
diverse condizioni al contorno. Le sezioni in cui sono specificate le condizioni
al contorno sono x0 e xNx −1 , ovvero, rispettivamente, quella all’estrema
sinistra del dispositivo e quella all’estrema destra del dispositivo.
45
• Bouncin.Questo è tipo di contatto più semplice. Esso si comporta
come una parete perfettamente riflettente. Una particella che collide con tale contatto avrà un cambiamento nel segno della velocità
perpendicolare (vedi figura 3.12).
Device
Sx contact
Dx contact
Figura 3.12: Contatto bouncing.
• Looping.Con questo tipo di contatto una particella che raggiunge il
contatto di sinistra viene reimmessa nel contatto di destra e viceversa
(vedi figura 3.13). Ci sono due possibili modalità per la reimmissione
della particella. Essa può essere reimmessa preservando il suo stato
(ponendo FALSE il bit equilibriumContact) o può essere reimmessa in
modo casuale in accordo con una distribuzione Maxwelliana ponendo
il bit TRUE
Device
Sx contact
Dx contact
Figura 3.13: Contatto looping.
• Equilibrium.Con questo tipo di contatti le due sezioni estreme si
comportano come delle riserve di particelle in equilibrio isolate dal
resto del dispositivo. Una particella che entra nel contatto viene distrutta (si veda figura 3.14(A)). Una particella che esce dal contatto
ed entra nel dispositivo viene immediatamente duplicata e reimmessa dal contorno con lo stesso momento (si veda figura 3.14(B)). Una
particella che raggiunge il contatto viene reimmessa dall’altro lato del
contatto con lo stesso momento (si veda figura 3.14(C)). Con tali ac46
A
B
C
1
2
Figura 3.14: Contatto equilibrium.
corgimenti il numero di particelle che stanno nei contatti resta sempre
costante. Queste due sezioni producono un numero stabile di particelle iniettate. La corrente dipenderà dalla differenza tra il flusso che
entra e quello che esce dal contatto. In questo tipo di contatto se il
bit equilibriumContact viene posto FALSE si impone che all’interno
del contatto il campo elettrico sia nullo, in modo tale da non cambiare
l’energia delle particelle.
• Asymmetrical.È una variante del caso Equilibrium. In questo caso
il contatto di sinistra resta come nel caso Equilibrium mentre quello di
destra diventa un contatto assorbente ideale. Ovvero tutte le particelle
che raggiungono il contorno destro del dispositivo vengono distrutti e
non vengono reimmessi (si veda figura 3.15).
Device
Sx contact
Dx contact
Figura 3.15: Contatto asymmetrical.
3.4.3
Descrizione dell’input file
Il file di input del simulatore è formato da una sequenza di cards ovvero
di parole chiave predefinite. Le cards sono sequenziali, quindi non possono
essere annidate le une con le altre; il loro ordine non è importante. Alcune
di esse inoltre possono essere ripetute. Ad ogni card segue una sequenza
di parametri che descrivono le caratteristiche della simulazione. Ogni card
deve terminare con un punto e virgola. Un esempio della card mesh è:
47
mesh
meshfile = ‘‘SCHR1D/mesh.grid’’
solfile = ‘‘SCHR1D/sol.dat’’;
in cui mesh è la card, meshfile e solfile sono i parametri della card e
SCHR1D/mesh.grid e SCHR1D/sol.dat sono i valori assegnati a tali parametri.
Di seguito si elencano le card presenti
• mesh(unica).Specifica i files con la griglia e la soluzione proveniente
da una simulazione effettuata con ISE-Dessis. Da questi files vengono
letti i profili di doping, la composizione dei materiali, la struttura
del dispositivo e una prima soluzione del profilo di potenziale. Viene
utilizzata assieme alle card xmesh e ymesh.
• xmesh e ymesh(ripetibili).Tramite esse è possibile specificare la griglia
utilizzata dal simulatore. É possibile definire il numero di sezioni lungo
le rispettive coordinate e le loro ampiezze. Le dimensioni e il sistema
di riferimento da prendere sono gli stessi del simulatore ISE-Dessis
• load1D(unica).É un alternativa all’uso delle prime tre. Con essa la
soluzione degli autovalori e delle autofunzioni è letta direttamente dal
simulatore SCHR1D. Il profilo di potenziale viene letto da un file di
input in cui si specificano le sezioni e il loro potenziale.
• valley(ripetibile).Specifica il modello da utilizzare per la struttura a
bande del materiale. Si possono specificare il numero di valli, il loro
relativo spostamento e la massa effettiva nelle direzioni x, y e z.
• parameters(unico).Con essa si possono specificare i parametri unici per tutto il programma come la temperatura, il numero seed di
generazione di numeri casuali, il fattore di non parabolicità etc.
• schr(unico).Si specificano i parametri per il risolutore dell’equazione
di Schrödinger.
• contact(ripetibile).Specifica la posizione dei contatti per il solutore
dell’equazione di Poisson. Viene utilizzato in concomitanza con la
card mesh.
• montecarlo(unico).Specifica i parametri della simulazione Monte Carlo. Si possono specificare il time-step, il numero di iterazioni, il numero
di particelle da simulare, il tipo di contatti, se trovare o meno soluzioni
auto-consistenti etc.
• kcontrol(unico).Specifica i parametri per la discretizzazione angolare
utilizzata per la computazione degli scattering nei meccanismi non
isotropici.
48
• phonon(unico).Specifica i parametri dello scattering fononico.
• roughness(unico).Specifica i parametri dello scattering con l’interfaccia.
• impurities(unico).Specifica i parametri dello scattering con impurità
ionizzate.
• tsufluctations(unico).Specifica i parametri per lo scattering da fluttuazione dello spessore di silicio t Si
• noscattering(ripetibile).Permette di attivare i meccanismi di scattering solo su determinate sezioni. Si rende utile nelle simulazioni in
regime balistico e in casi in cui si voglia velocizzare le simulazioni,
annullando lo scattering dove si reputa che esso non sia influente.
• inspect(ripetibile).Salva in un file il diagramma a bande e il profilo
di carica in direzione y delle sezioni specificate.
• plot(unico).Specifica quali grandezze vadano scritte in formato PlotMTV
o testo. Scrive direttamente le grandezze di ogni nodo della griglia
specificata in xmesh e ymesh.
49
50
Capitolo 4
Simulazione della mobilità
apparente in transistori
decananometrici
Questo capitolo inizia con la descrizione del metodo utilizzato per la misura
della mobilità. Si passa in seguito allo studio del comportamento dei dispositivi considerando un’unica sottobanda. Si considera poi il caso strain
e quello unstrain. Per finire si affronterà il comportamento della mobilità
al variare della temperatura, argomento che crea peraltro un legame col
capitolo successivo.
4.1
Estrazione della mobilità dalle simulazioni
Come visto nella sezione 2.2 la mobilità viene determinata tramite la relazione sperimentale
L gd (VG ) µ=
(4.1)
W qNs (VG ) lowf ield
in condizione di bassissimi campi longitudinali. Con il simulatore Monte
Carlo presentato nel capitolo 3 è possibile effettuare simulazioni per discutere il significato della mobilità apparente estratto in dispositivi di diverse
lunghezza.
4.1.1
Mobilità apparente
Nelle nostre simulazioni per mobilità apparente µ app intendiamo la mobilità
misurata in dispositivi di diverse lunghezze usando per il source e drain dei
contatti di tipo Equilibrium. In figura 4.1 è riportato lo schema esplicativo
di queste simulazioni.
51
Fx
E C(x)
Source
(equilibriumContact)
Drain
(equililbriumContact)
Figura 4.1: Rappresentazione schematica della modalità di simulazioni della
mobilità apparente
4.1.2
Mobilità di canale lungo
Per mobilità di canale lungo µ0 intendiamo la mobilità caratteristica di un
dispositivo lungo. Per simularla utilizziamo la modalità Looping ponendo
questa volta i contatti non in equilibrio. In questo modo è possibile simulare
dispositivi di lunghezza infinita. In figura 4.2 è riportato la schematizzazione
di tale simulazione. La mobilità che se ne ricava è influenzata solo dai mecFx
E C(x)
Source
(~equilibriumContact)
Drain
(~equililbriumContact)
Looping ( L=
)
Figura 4.2: Rappresentazione schematica della modalità di simulazione della
mobilità di canale lungo
canismi di scattering presenti e in quanto la mobilità balistica è ininfluente
per lunghezze infinite.
52
4.2
Mobilità di singola sottobanda
Questo tipo di studio ha valenza principalmente teorica in quanto esso è
utile per verificare quanto affermato nella sezione 2.6. In quest’ultima si
arriva all’espressione finale per la mobilità apparente
−1
−1
µ−1
= (µ0 rLF )−1
app = µO + (µBAL,L L)
(4.2)
dove µ0 è la mobilità di canale lungo, µBAL,L è la mobilità balistica per unità
di lunghezza, L la lunghezza di canale e r LF il coefficiente di riflessione di
basso campo pari a
L
(4.3)
rLF =
L+λ
dove λ è la lunghezza del libero cammino medio. Nel caso degenere l’espressione si complica in quanto entrano in gioco gli integrali di Fermi-Dirac. In
tal caso diventa
µ−1
app
=
µ−1
O +
µBAL,L
=− 1 (ηF )
2
=0 (ηF )
L
!−1
−1
= µ−1
= (µ0 rLF,deg )−1
O +(µBAL,L,DEG L)
(4.4)
con il coefficiente di riflessione che questa volta vale
rLF,deg =
L
L + λ ==01(η(ηFF) )
(4.5)
−2
Passiamo ora a fare una stima quantitativa della µ BAL,L nel caso non degenere. Come visto essa ha l’espressione
µBAL,L =
vth
2VT H
(4.6)
dove vth è la velocità termica. Nel caso in esame in cui consideriamo solo la
prima sottobanda (first unprimed), abbiamo una massa efficace per l’elettrone m∗ = 0.19m0 . Quindi la velocità termica alla temperatura T = 300K
sarà
s
m
2KT
vT =
≈ 1.23 105
(4.7)
∗
πm
s
Sostituendo il valore della velocità termica nell’equazione (4.6) troviamo
il valore della mobilità balistica per unità di lunghezza, ovvero µ BAL,L =
23.9 cm2 /(V s nm).
Le simulazioni di estrazione della mobilità apparente sono state fatte al
variare della lunghezza e per diverse tensioni di gate applicate, per verificare
che la mobilità balistica per unità di lunghezza del caso non degenere non
dipenda dalla tensione applicata e per vedere come quella del caso degenere
risulti invece influenzata dalla degenerazione. Per queste simulazioni sono
53
stati utilizzati dei dispositivi MOS BULK con drogaggio di canale 2 × 10 16
e con contatti ideali, senza regioni di source e drain, per non dover tenere
conto delle resistenze serie. Lo spessore di ossido t ox è di 3nm e si è utilizzato
un ossido con r = 7.0. In figura 4.3 è presente lo schema del dispositivo utilizzato. Di seguito si riporta una tabella riassuntiva delle tensioni applicate
gate
oxide
source
tox = 3 nm
drain
substrato
doping = 2e16
Figura 4.3:
simulazioni.
Schema del dispositivo BULK template utilizzato nelle
con la relativa densità di inversione. In figura 4.4 si riportano le curve di
VG [V ]
0.3
0.5
0.7
1.4
2.2
3.4
h
i
#
N2D cm
2
1.13 × 1012
2.21 × 1012
3.37 × 1012
7.63 × 1012
12.67 × 1012
20.38 × 1012
Tabella 4.1: N2D alle varie tensioni VG utilizzate
mobilità apparente ottenute. Si sono simulati i casi degeneri e non degeneri
per le quattro tensioni indicate in tabella 4.1. Nelle simulazioni si è tenuto
conto dello scattering fononico essendo esso il principale meccanismo. Si
può notare come mano a mano che la tensione di gate V G si alza, la mobilità degenere differisce sempre di più dalla mobilità non degenere. Si nota
inoltre che le curve hanno progressivamente una forma diversa. Questo fatto è dovuto dalla variazione della mobilità balistica per unità di lunghezza
µBAL,L e sarà più chiaro osservando il grafico ottenuto con l’inverso delle
mobilità apparenti.
Dalla (4.2) e (4.4) si vede immediatamente che è possibile ricavare il
valore della mobilità balistica per unità di lunghezza estraendo la pendenza
dell’inverso della mobilità apparente al variare dell’inverso della lunghezza di
54
1190
VG=0.3 V, NON DEG
VG=0.3 V, DEG
VG=0.5 V, NON DEG
VG=0.5 V, DEG
VG=0.7 V, NON DEG
VG=0.7 V, DEG
VG=1.4 V, NON DEG
VG=1.4 V, DEG
VG=2.2 V, NON DEG
VG=2.2 V, DEG
VG=3.4 V, NON DEG
VG=3.4 V, DEG
790
2
µapp [cm /(Vs)]
990
590
390
190
30
80
L [nm]
130
180
Figura 4.4: Mobilità apparenti in funzione della lunghezza di canale al variare delle tensioni di gate applicate (simboli). In continuo le curve relative
ai casi non degeneri, in tratteggiato le curve in cui si è tenuto conto della degenerazione. Le mobilità di canale lungo µ 0 per i casi trattati sono:
(VG = 0.3 V , NON DEG.): µ0 = 1562 cm2 /(V s), (VG = 0.3 V , DEG.):
µ0 = 1548 cm2 /(V s); (VG = 0.5V , NON DEG.): µ0 = 1373 cm2 /(V s),
(VG = 0.5 V , DEG.): µ0 = 1351 cm2 /(V s); (VG = 0.7 V , NON DEG.):
µ0 = 1251 cm2 /(V s), (VG = 0.7 V , DEG.): µ0 = 1224 cm2 /(V s);
(VG = 1.4 V , NON DEG.): µ0 = 1034 cm2 /(V s), (VG = 1.4 V , DEG.):
µ0 = 981 cm2 /(V s); (VG = 2.2 V , NON DEG.): µ0 = 913 cm2 /(V s),
(VG = 2.2 V , DEG.): µ0 = 840 cm2 /(V s); (VG = 3.4 V , NON DEG.):
µ0 = 785 cm2 /(V s), (VG = 3.4 V , DEG.): µ0 = 715 cm2 /(V s).
canale. Invece l’intercetta con l’asse delle ordinate fornisce il valore dell’inverso della mobilità di canale lungo µ 0 , come schematicamente indicato in
figura 4.5. La figura 4.6 mostra appunto l’inverso della mobilità in funzione
dell’inverso della lunghezza: la linearità dei dati è ottima. Si può notare
che le rette dei casi non degeneri hanno la stessa pendenza. Ciò è corretto
in quanto la mobilità balistica per unità di lunghezza non deve dipendere
in questo caso dalla tensione applicata. Le rette invece che sono relative
al caso degenere hanno pendenze diverse come si può notare nel grafico di
figura 4.7. In questo caso, come da equazione 4.4, si può scrivere
µBAL,L,DEG =
vth =− 21 (ηF )
2VT H =0 (ηF )
(4.8)
dove il rapporto =− 1 (ηF )/=0 (ηF ) tra gli integrali di Fermi-Dirac esprime
2
la dipendenza dalla degenerazione. I valori estratti per le mobilità balistiche per unità di lunghezza sono riportati in tabella 4.2. Si può notare nel
55
−1
µ app
−1
µ BAL,L
µ 0 −1
L −1
Figura 4.5: Metodo di estrazione della mobilità balistica. Essa è la pendenza dell’inverso della mobilità apparente µ ef f al variare dell’inverso della
lunghezza di canale. L’intercetta della retta con l’asse delle ordinate da il
valore dell’inverso della mobilità di canale lungo.
caso non degenere un andamento pressoché costante (a meno di modeste
deviazioni). I valori del caso degenere, invece, sono fortemente variabili.
Per la precisione sono decrescenti in quanto il rapporto = − 1 (ηF )/=0 (ηF ) è
2
decrescente all’aumentare di ηF ovvero all’aumentare della degenerazione.
Essendo
EF − E C
ηF =
(4.9)
KT
è possibile andare ad estrarre dalle simulazioni tale valore per poi trovare
il rapporto =− 1 (ηF )/=0 (ηF ) mediante interpolazione. Tale rapporto può
2
essere confrontato con il rapporto µ BAL,L,DEG /µBAL,L per verificare quanto
i risultati ottenuti siano consistenti al modello utilizzato. In tabella 4.3 si
riassumono i risultati ottenuti. In figura 4.8 viene graficato questo confronto
e si può vedere che il rapporto tra le due mobilità segue molto bene il
rapporto teorico espresso tramite gli integrali di Fermi-Dirac.
56
VG=0.3 V, NON DEG
VG=0.3 V, DEG
VG=0.5 V, NON DEG
VG=0.5 V, DEG
VG=0.7 V, NON DEG
VG=0.7 V, DEG
VG=1.4 V, NON DEG
VG=1.4 V, DEG
VG=2.2 V, NON DEG
VG=2.2 V, DEG
VG=3.4 V, NON DEG
VG=3.4 V, DEG
0.0025
−1
2
µapp [Vs/cm ]
0.0035
0.0015
0.0005
0.005
0.01
−1
0.015
0.02
−1
L [nm ]
Figura 4.6: Andamento dell’inverso della mobilità apparenti al variare dell’inverso della lunghezza di canale per diverse tensioni di gate V G (diversi
simboli). Per ogni tensione è raffigurato il caso degenere (linea tratteggiata)
e il caso non degenere (linea continua).
VG=0.3 V, DEG
VG=0.5 V, DEG
VG=0.7 V, DEG
VG=1.4 V, DEG
VG=2.2 V, DEG
VG=3.4 V, DEG
µ
−1
app
2
[Vs/cm ]
0.0035
0.0025
0.0015
0.0005
0.005
0.01
−1
0.015
0.02
−1
L [nm ]
Figura 4.7: Andamento dell’inverso della mobilità apparente al variare dell’inverso della lunghezza di canale per diverse tensioni di gate V G (diversi
simboli). Sono riportati solo i casi degeneri per evidenziare le differenti
pendenze.
57
VG [V ]
0.3
0.5
0.7
1.4
2.2
3.4
µBAL,L [cm2 /(V s nm)]
21.7
21.1
21.0
23.3
21.9
21.1
µBAL,L,
DEG
[cm2 /(V s nm)]
21.6
20.6
19.6
16.6
14.2
10.8
Tabella 4.2: Valore delle mobilità balistiche estratte dei casi non degeneri e
degeneri per varie tensioni da gate applicate
VG [V ]
0.3
0.5
0.7
1.4
2.2
3.4
ηF
-1.14
-0.34
0.24
1.69
3.04
4.95
=− 1 (ηF )/=0 (ηF )
2
0.94
0.89
0.85
0.71
0.60
0.50
µBAL,L,DEG /µBAL,L
0.99
0.98
0.93
0.71
0.65
0.51
Tabella 4.3: Risultati ottenuti estraendo η F dalle simulazioni, interpolandolo per trovare il valore =− 1 (ηF )/=0 (ηF ). Si confronta il risultato con il
2
rapporto µBAL,L,DEG /µBAL,L
58
12
1
N2D=1.13x10
12
N2D=2.21x10
12
N2D=3.36x10
0.8
µBAL,L, DEG/µBAL,L
12
N2D=7.63x10
12
N2D=12.67x10
0.6
N2D=20.38x10
0.4
0.2
−10
12
µBAL,L,DEG/µBAL,L
F−1/2(ηF)/F0(ηF)
0
ηF
10
20
Figura 4.8: Confronto dei valori del rapporto tra le mobilità (simboli),
con il rapporto teorico dato dal rapporto tra gli integrali di Fermi-Dirac
=− 1 (ηF )/=0 (ηF ) (linea tratteggiata). I valori sono riportati in tabella 4.3.
2
59
4.3
Mobilità per dispositivi strain
Dopo aver confermato il funzionamento della teoria della mobilità balistica
per la singola sottobanda si è proceduto a studiare il comportamento della
stessa nel caso di silicio strained ed unstrained. L’effetto dello strain è stato
x
x
Primed
Primed
Unprimed
Unprimed
y
y
z
z
Strain
Unstrain
Figura 4.9: Schema delle valli energetiche nel caso unstrain e in quello strain.
Si nota un abbassamento energetico delle valli unprimed.
incluso nel simulatore per mezzo di un abbassamento energetico delle sottobande unprimed, che hanno una massa equivalente nel piano del trasporto
inferiore (m∗ = 0.19m0 ), come si può vedere da figura 4.9. In questo modo vengono occupate prima le sottobande unprimed, con il risultato di una
massa equivalente complessiva inferiore e quindi una mobilità maggiore. In
figura 4.10 vengono riportati i diagrammi a bande dei due casi. Come si
può notare le sottobande unprimed nel caso strain si sono notevolmente
abbassate in energia.
Per le simulazioni si è usato un dispositivo SOI DG, vedi figura 4.11 con
tSi = 10.0 nm e una tox = 0.7 nm con dielettrico caratterizzato da r = 7.0
e doping di canale 1 × 1015 . La tensione applicata al gate è VG = 1.0 V . La
procedura utilizzata per l’estrazione dei risultati è del tutto analoga a quella
utilizzata nel caso della sezione 4.2. In figura 4.12 si riporta l’andamento
della mobilità al variare della lunghezza di canale. Si noti come in generale
la mobilità nel caso strain sia migliore; tuttavia al ridursi della lunghezza
del dispositivo le due mobilità convergono. In figura 4.13 viene riportato
l’andamento dell’inverso della mobilità apparente al variare dell’inverso della
lunghezza di canale. In tabella 4.4 vengono riportati i risultati ottenuti
estraendo le mobilità balistiche per unità di lunghezza. Dai valori estratti
si noti come nel caso unstrain si abbia una riduzione del valore di µ BAL,L
rispetto al limite teorico di singola sottobanda ricavato nella sezione 4.2.
Tale riduzione è dovuta all’effetto della media su bande superiori aventi
masse efficaci per il trasporto superiori. Il caso strain non degenere è più
60
Figura 4.10: Grafico delle sottobande per il caso unstrain e quello unstrain
per il dispositivo SOI DG simulato.
Top Gate
Oxide
Source
t ox =0.7nm
Channel
Drain
tSi =6.3nm
Oxide
Down Gate
Figura 4.11: Rappresentazione del dispositivo SOI DG template utilizzato
nelle simulazioni.
vicino al limite teorico di singola sottobanda in quanto le sottobande di tipo
primed sono spostate ad una energia più alta.
61
600
2
µapp [cm /(Vs)]
500
400
UNSTRAIN, NON DEG
UNSTRAIN, DEG
STRAIN, NON DEG
STRAIN, DEG
300
200
7.5
57.5
L [nm]
107.5
157.5
Figura 4.12: Mobilità apparenti per dispositivo SOI DG in funzione della
lunghezza di canale per una tensione applicata di V G = 1.0 V . In continuo le curve relative ai casi non degeneri, in tratteggiato le curve in cui si è
tenuto conto della degenerazione. Le mobilità di canale lungo per i casi trattati sono: (UNSTRAIN, NON DEG.): µ0 = 602 cm2 /(V s), (UNSTRAIN,
DEG.): µ0 = 513 cm2 /(V s), (STRAIN, NON DEG.): µ0 = 726 cm2 /(V s),
(STRAIN, DEG.): µ0 = 636 cm2 /(V s).
MODE
U N ST RAIN N ON DEG
U N ST RAIN
DEG
ST RAIN
N ON DEG
ST RAIN
DEG
µBAL,L [cm2 /(V s nm)]
17.1
17.3
22.8
17.7
Tabella 4.4: Tabella riassuntiva delle mobilità balistiche per unità di
lunghezza estratte.
62
0.0044
2
µapp [Vs/cm ]
0.0034
−1
0.0024
UNSTRAIN, NON DEG
UNSTRAIN, DEG
STRAIN, NON DEG
STRAIN, DEG
0.0014
0.0004
0
0.01
−1
0.02
−1
L [nm ]
0.03
0.04
Figura 4.13: Inverso delle mobilità apparenti per dispositivo SOI DG in
funzione della lunghezza di canale per una tensione applicata di V G = 1.0 V .
In continuo le curve relative ai casi non degeneri, in tratteggiato le curve in
cui si è tenuto conto della degenerazione. Si noti come la curva relativa al
caso non degenere strain abbia una pendenza leggermente inferiore ovvero
una mobilità balistica per unità di lunghezza maggiore.
63
4.4
Mobilità al variare della temperatura
Nella presente sezione si analizza il comportamento della mobilità apparente
al variare della temperatura. Essendo, come visto,
−1
−1
µ−1
app = µO + (µBAL,L L)
(4.10)
l’andamento in temperatura della mobilità apparente sarà il risultato della
combinazione degli andamenti in temperatura delle due componenti, ovvero
della mobilità di canale lungo e della mobilità balistica. Ovviamente quanto
più il dispositivo è lungo tanto più il suo comportamento è vicino a quello
della mobilità di canale lungo, quanto più è corto, tanto più mostrerà un
comportamento dettato dalla mobilità balistica. Essendo infatti
vth =
T
T0
γv
th
vth,T0
(4.11)
si hanno le dipendenze
vth
→ µBAL,L ∝ T (γvth −1)
2VT H
γµ
0
T
µ0 =
µ0,T0 → µ0 ∝ T γµ0
300K
µBAL,L =
(4.12)
In figura 4.14 si graficano gli andamenti teorici della mobilità apparente
normalizzata al variare della temperatura, per varie lunghezze di canale, ed
in scale logaritmiche per far notare come abbiano pendenze sempre minori
al decrescere della lunghezza. Si sono ipotizzati µ 0,T0 = 900 cm2 /(V s),
γµ0 = −1.6, vth = 1.2 105 m/s e γvt h = 0.4. Per verificare il comportamento
previsto analiticamente sono state effettuate delle simulazioni Monte Carlo
per diverse lunghezze al variare della temperatura. Il dispositivo utilizzato
è lo stesso SOI DG utilizzato nella sezione 4.3 con tensione di gate applicata
di VG = 1.1 V . In figura 4.15 sono riportati gli andamenti in funzione della
temperatura per dispositivi di lunghezza L G = 45, 90 e 180 nm. É stato
simulato anche il dispositivo in modalità looping per avere la mobilità di
canale lungo. Si può apprezzare una leggera diminuzione di pendenza al
tendere del dispositivo al caso balistico. In tabella 4.5 vengono riportate le
pendenze delle rette in scala logaritmica. Tale pendenza corrisponde a γ µapp
dove
γµapp
T
(4.13)
µapp =
µapp,T0
300K
I valori trovati sono congruenti con γ vth = 0.4 che è stato estratto dalle
simulazioni. Con tale valore è immediato trovare γ µBAL,L = −0.6 che è la
minima pendenza che si riscontrerebbe per lunghezze di canale infinitamente
piccole. I valori trovati per i dispositivi di lunghezza finita infatti sono
compresi tra -1.6 e -0.6.
64
0.28
L=INF
L=1 µm
L=180 nm
L=90 nm
L=45 nm
L=4 nm
L=0 (ballistic)
0
log10(µapp/µapp,T )
0.18
0.08
−0.02
−0.12
−0.22
2.27
2.37
2.47
log10(T) [K]
2.57
Figura 4.14: Andamento analitico della mobilità apparente al variare della
temperatura. La mobilità apparente è normalizzata al suo valore a T 0 =
300K. Le scale sono logaritmiche.
LG [nm]
27
45
90
180
∞
γµapp
-0.90
-1.07
-1.23
-1.36
-1.6
Tabella 4.5: Valori estratti dall’andamento delle mobilità apparenti al
variare della temperatura.
65
3.4
INF (µ0)
LG=180nm
LG=90nm
LG=45nm
LG=27nm
3
2
log10(µapp) [cm /(Vs)]
3.2
2.8
2.6
2.4
2.27
2.37
log10(T) [K]
2.47
2.57
Figura 4.15: Andamento della mobilità apparente al variare della temperatura per dispositivi di lunghezza 27nm 45nm, 90nm e 180nm. In continuo
simulazione di canale lungo µ0 . Le scale sono logaritmiche. Si nota che le
pendenze diminuiscono leggermente al diminuire della lunghezza di canale.
(si veda tabella 4.5)
66
Capitolo 5
Simulazione della
metodologia di estrazione
sperimentale del coefficiente
di riflessione
Nel presente capitolo si verifica il metodo per l’estrazione del coefficiente di
riflessione presentato nella sezione 2.7. Si parte da un modello semplice per
le verifiche di base per poi passare ad un modello con un effettivo virtual
source. Infine si simula un dispositivo reale. Il metodo viene applicato alle
caratteristiche corrente-tensione ottenute tramite simulazioni Monte Carlo
ed i coefficienti cosı̀ estratti sono confrontati con quelli forniti dal simulatore
sulla base del trasporto di carica interno al dispositivo.
5.1
Profilo di potenziale lineare
Prima di passare alla verifica della validità del metodo ricavato per dei profili di potenziale realistici, si è applicato il metodo al caso di un semplice
profilo lineare di potenziale, di seguito denominato scivolo di potenziale. La
situazione in questione è rappresentata in figura 5.1. In essa si nota come
non sia presente una zona fuori dai contatti con campo elettrico nullo ovvero
non esista il virtual source. Per una situazione di questo tipo, l’equazione
(2.50) non è più valida in quanto non c’è più carica che torna indietro verso
il source. Il flusso che dal source arriva al drain è diminuito del coefficiente
di trasmissione del canale t. Questa situazione semplificata è resa possibile
dalla proprietà dei contatti in modalità Equilibrium (si veda sez. 3.4.2).
Analogamente a quanto visto nella sezione 2.5 si usa la flux theory ma in
questo caso si ha
aD = a S ts t
(5.1)
67
Sections
aS
channel
Source
Drain
EC(x)
aD
0
x
Figura 5.1: Schematizzazione del dispositivo utilizzato e dei flussi in esso
presenti. In grossetto il profilo di energia potenziale a scivolo utilizzato. In
tratteggiato le fette in cui è stato diviso il dispositivo.
e
n(0, y) =
ts aS
a+
=
vth
vth
(5.2)
Ricavando tS da (5.2) e sostituendolo in (5.1), valendo che t = 1 − r, si può
ricavare
aD = n(0, y)vth (1 − r)
(5.3)
Integrando l’eq. (5.3) in y ed ipotizzando di essere sopra soglia si ricava
ID = W Cef f (VGS − VT ) vth (1 − r)
λ
lKT
= W Cef f (VGS − VT ) vth
1+
λ
lKT
!
(5.4)
Si passa ora a fare la derivata rispetto alla temperatura della (5.4) ottenendo
1 ∂ID
W ∂T
=
−Cef f vth
λ
∂VT
∂vth
lKT
+
+ Cef f (VGS − VT )
∂T
∂T 1 + l λ
KT
+Cef f (VGS
∂
− VT ) vth
∂T
λ
lKT
1+
λ
lKT
!
(5.5)
Questo caso semplificato permette di considerare unitario l’andamento in
temperatura del KT-layer in quanto il campo elettrico è fissato, quindi le
68
dipendenze in temperatura sono
µ 0 ∝ T γµ 0
vth ∝ T γvth
∝ T1
VT µ0
λ ∝
∝ T (1+γµ0 −γvth ) = T γλ
vth
lKT
(5.6)
Dalle relazioni in (5.6) possiamo esprimere le derivate in temperatura come
T γλ
∂λ
λ
λ =
λ0 =⇒
= γλ
T
∂T
T
0
∂lKT
lKT
T
lKT0 =⇒
=
lKT =
T
∂T
T
0 γv
th
vth
∂vth
T
vth =
vth0 =⇒
= γvth
T0
∂T
T
(5.7)
Con le (5.7) si può ricavare la derivata rispetto alla temperatura del rapporto
λ/lKT
λ
∂
λ
=
(γλ − 1)
(5.8)
∂T lKT
lKT · T
e quindi ottenere la derivata rispetto alla temperatura del rapporto λ/l KT / (1 + λ/lKT )
come
∂
∂T
λ
lKT
1+
λ
lKT
!
=
=
1
∂
λ ∂T
1 + lKT
λ
lKT
1+
λ
lKT
2
λ
lKT
−
1+
λ
1
λ
lKT
(1 − γλ )
T
2
lKT
∂
∂T
λ
lKT
(5.9)
Sostituendo la (5.9) nella (5.5) si ottiene
λ
lKT
1 ∂ID
= Cef f (VGS − VT ) vth
W ∂T
!
−

η
γv
γλ − 1 
+ th + λ
λ
VGS − VT
T
1 + lKT
T 1 + lKT
(5.10)
Normalizzando la 5.10 con l’espressione della corrente si ottiene
∆ID
α=
∆T · ID
"
#
=
1
γλ − 1
γvth +
λ
T
1 + lKT
=
γµ − γ v
1
η
γvth + 0 λ th −
T
VGS − VT
1 + lKT
"
−
#
69
η
VGS − VT
(5.11)
Esplicitando il rapporto λ0 /lKT0 rispetto alla temperatura T0 si ottiene
λ0
lKT0
=
=
γ
vth
− γ µ0
γvth − α +
γvth −
η
VGS −VT0
γvth
∆ID
∆T ·ID0
− γ µ0
−
T0
−1
∆QIN V
∆T ·QIN V0
T0
−1
(5.12)
dove si è potuto scrivere la seconda equazione utilizzando
∆QIN V
η
=−
VGS − VT0
∆T · QIN V0
(5.13)
Per verificare quanto esposto si è utilizzato lo stesso dispositivo SOI DG
utilizzato per le simulazioni della sezione 4.3, che è illustrato in figura 5.2.
Esso ha un drogaggio di canale di 1 × 10 15 , uno spessore di dielettrico tox =
Top Gate
Oxide
Source
t ox =1.0nm
Drain
Channel
tSi =6.3nm
Oxide
Down Gate
Figura 5.2: Schematizzazione del dispositivo utilizzato.
1.0 nm con un dielettrico con r = 3.9, uno spessore di canale tSi = 6.3 nm e
la lunghezza di canale LG = 90 nm. Ad esso si applica una tensione di gate
VGS = 1.1 V . Per questa prima prova si tiene conto solo dello scattering
fononico. Il primo passo per l’applicazione dell’espressione (5.12) è quello
di fare uno studio analogo a quelli condotti nella sezione 4.4 per trovare la
dipendenza dalla temperatura della mobilità di canale lungo. In figura 5.3
si riporta tale andamento in scale logaritmiche da cui è possibile estrarre
γµ0 = −1.6.
Per studiare le altre grandezze è necessario simulare il dispositivo applicadogli una tensione di drain VDS = 0.8 V . Dai dati delle simulazioni
si possono ricavare l’andamento in temperatura della velocità termica γ vth
(si veda figura 5.4), il valore del rapporto incrementale normalizzato della
corrente ∆ID /(∆T ID0 ) (si veda figura 5.5), e il valore del rapporto incrementale normalizzato della carica di inversione ∆Q IN V /(∆T QIN V0 ) (si veda
figura 5.6).
70
3.3
Simulazione MC
Retta interpolante
3.1
2
log10(µ0) [cm /(Vs)]
3.2
3
2.9
2.8
2.3
2.4
2.5
log10(T) [K]
2.6
Figura 5.3: Andamento della mobilità di canale lungo µ 0 al variare della
temperatura in scale logaritmiche, V GS = 1.1 V con densità di carica di
inversione a T0 = 300K, N2D0 = 14.7 × 1012 [#/cm2 ]. Dalla regressione dei
punti si ricava γµ0 = −1.6.
γ µ0
-1.6
γvth
0.4
∆ID /(∆T ID0 ) = α
−1.38 × 10−3
∆QIN V /(∆T QIN V0 )
2.3 × 10−4
Tabella 5.1: Dati estratti dal dispositivo SOI DG, L G = 90 nm
In tabella 5.1 si riassumono i dati ricavati. Ora è possibile applicare
la (5.12) per ottenere il rapporto λ 0 /lKT0 alla temperatura T0 = 300K e
successivamente il coefficiente di rilfessione come
r0 =
1
1 + λ0 /lKT0
(5.14)
In tabella 5.2 si riportano tali risultati e li si confronta con il valore del
coefficiente di riflessione ottenuto direttamente dalla simulazione. Infatti
il coefficiente di riflessione per alti campi è definito come il rapporto tra
la corrente che torna indietro dal drain verso il virtual source, I − (0), e la
corrente che dal virtual source va verso il drain, I + (0), entrambe misurate
in corrispondenza del virtual source, ovvero
rM C =
I − (0)
I + (0)
(5.15)
Tale rapporto viene calcolato numericamente dal simulatore sulla base dei
flussi di portatori. Come si può vedere il risultato ottenuto è molto vicino a quello calcolato numericamente dal simulatore. Dai risultati ottenuti
71
4.1
log10(vth) [m/s]
4.08
4.06
Da simulazione MC
retta interpolante
4.04
4.02
4
2.34
2.39
2.44
2.49
log10(T) [K]
2.54
2.59
2.64
Figura 5.4: Andamento della velocità termica al variare della temperatura
in scale logaritmiche. In tratteggiato la regressione dalla cui pendenza si
ricava γth = 0.4. La densità di carica di inversione a T 0 = 300K è N2D0 =
14.7 × 1012 [#/cm2 ].
λ0 /lKT0
1.27
r0 = 1/(1 + λ0 /lKT0 )
0.44
r M C0
0.45
Tabella 5.2: Risultati ottenuti per il dispositivo SOI DG, L G = 90 nm
si è accertata la validità del metodo. Si può ora passare allo studio del
comportamento in presenza di virtual source.
72
0.1
Da simulazione MC
retta interpolante
∆ID/ID
0
0.05
0
−0.05
−0.1
230
280
T [K]
330
380
Figura 5.5: Andamento della derivata normalizzata della corrente in temperatura. In tratteggiato la regressione da cui si ricava ∆I D /(∆T ID0 ) =
−1.38 10−3 . La densità di carica di inversione a T 0 = 300K è N2D0 =
14.7 × 1012 [#/cm2 ].
0.02
∆QINV/QINV
0
0.01
0
Da simulazione MC
retta interpolante
−0.01
−0.02
230
280
T [K]
330
380
Figura 5.6: Andamento della derivata normalizzata della carica di inversione in temperatura. In tratteggiato la regressione da cui si ricava
∆QIN V /(∆T QIN V0 ) = 2.3 10−4 . La densità di carica di inversione a
T0 = 300K è N2D0 = 14.7 × 1012 [#/cm2 ].
73
5.2
Profilo di potenziale lineare con virtual source
Per verificare la solidità del metodo con virtual source ovvero della
λ0
lKT0
=
−2 (1 + γµ0 − γvth − γlKT )
γvth −
∆ID
∆T ·ID0
−
∆QIN V
∆T ·QIN V0
T0
−2
(5.16)
si è iniziato impostando il potenziale in modo tale da creare un virtual source
fissato. In figura 5.7 si riporta la schematizzazione del profilo di potenziale
e campo elettrico.
Fx
Source
E C(x)
Drain
Virtual Source (VS)
Fx
0
x
Figura 5.7: Rappresentazione del profilo di energia potenziale imposto. In
basso il modulo del campo elettrico che ne consegue. Il campo elettrico è in
direzione −x.
Tale profilo permette di avere un campo elettrico nullo in prossimità della
prima sezione fuori dal contatto di source. Anche in questo caso, imponendo
un potenziale fisso, il KT-layer varia con la temperatura come T 1 , ovvero si
ha γlKT = 1. Analogamente a quanto fatto per il caso precedente abbiamo
studiato le altre quantità presenti nella (5.16). É anche possibile confrontare
74
i risultati ottenuti con quelli che si ottengono dalla
λ0
lKT0
=
4
0.5 −
∆ID
∆T ·ID0
−
∆QIN V
∆T ·QIN V0
T0
−2
(5.17)
che è l’uguaglianza ricavata dal lavoro di Chen et al. [25]. Per studiarne
il comportamento e le differenze in maniera completa si effettuano prove
su dispositivi di lunghezze diverse. Inizialmente si tiene in considerazione
soltanto lo scattering fononico senza attivare la degenerazione. É necessario,
prima di procedere oltre, aprire una breve parentesi sulla modalità dell’estrazione dei dati. Più precisamente, quando si va ad estrarre il parametro
∆ID /(∆T ID0 ) si nota che l’andamento di ∆ID /ID0 non è funzione lineare
della temperatura come si può vedere da figura 5.8 relativa ad un dispositivo con LG = 50nm. La dipendenza non lineare dalla temperatura è
evidenziabile dall’equazione
∆T
∆ID
=
I D0
T0
γvth
2 (γµ0 − γvth )
+
λ
2 + lKT
!
+
∆QIN V
.
QIN V0
(5.18)
∆T ha dipendenza ovviamente lineare da T , λ/l KT è proporzionale a T (γµ0 −γvth )
e ∆QIN V /QIN V0 ha dipendenza lineare da T . Inoltre la combinazione dei
due addendi di (5.18) avviene in maniera diversa a seconda della lunghezza
del dispositivo che influisce su lKT . L’estrazione della pendenza di ∆I D /ID0
ha, quindi, un valore non corretto se fatta con tutti i punti a disposizione. In
questo caso e in casi analoghi si preferisce estrarre la pendenza in un intorno
della temperatura T0 più stretto prendendo le prime due temperature vicine
a T0 e trovare la pendenza con tre punti. Nel seguito ci si riferisce a tale
metodologia con “best fit”. In tabella 5.3 e 5.4 si riassumono i vari parametri
estratti, i valori del rapporto λ0 /lKT0 e il coefficiente di riflessione ricavato
con le due espressioni. In tabella 5.3 si nota che il parametro α estratto ha
LG [nm]
9
18
27
45
90
180
γ µ0
-1.6
-1.6
-1.6
-1.6
-1.6
-1.6
γvth
0.4
0.4
0.4
0.4
0.4
0.4
∆ID /(∆T ID0 ) = α
6.3 × 10−4
3.4 × 10−4
1.3 × 10−6
−4.9 × 10−4
−1.3 × 10−3
−2.5 × 10−3
∆QIN V /(∆T QIN V0 )
9.2 × 10−4
1.1 × 10−3
1.2 × 10−3
1.3 × 10−3
1.3 × 10−3
1.3 × 10−3
Tabella 5.3: Dati ottenuti per il dispositivo SOI DG per varie lunghezze
di canale LG , solo scattering fononico. VDS = 0.8 V , VGS = 1.1 V con
densità di carica di inversione al virtual source, a T 0 = 300K, N2D0 =
14.7 × 1012 [#/cm2 ]. Non si considera la degenerazione.
75
0.02
0.01
T0
∆ID/ID
0
0
−0.01
−0.02
retta interpolante (6 punti)
retta interpolante (3 punti)
−0.03
−0.04
180
230
280
T [K]
330
Figura 5.8: Andamento di ∆ID /ID0 per un dispositivo con LG = 50nm.
In casi come questo per determinare la pendenza si preferisce restringere
l’intorno della temperatura T0 ai primi due punti, per un totale di tre punti,
per avere un valore corretto di ∆ID /(∆T ID0 ).
un adamento variabile al variare della lunghezza di canale. Il fatto si può
spiegare andando a vedere la sua epressione analitica già ricavata in sezione
2.7.1


2 (γµ0 − γvth ) 
∆QIN V
1 
γvth +
+
(5.19)
α=
λ
0
T0
∆T QIN V0
2 + lKT
0
In tale equazione l’unico parametro che varia significativamente, al variare
della lunghezza del dispositivo, è il rapporto λ 0 /lKT0 . Precisamente λ0 /lKT0
è tanto più grande quanto più il dispositivo è piccolo in quanto il termine
lKT0 decresce con LG . Al diminuire di λ0 /lKT0 diminuisce il denominatore
di cui è parte, facendo crecere il contributo negativo della frazione.
In figura 5.9 viene riportato l’andamento del coefficiente di riflessione
al variare della lunghezza di canale L G . Si può notare come tra i risultati
ottenuti con l’equazione proposta da Chen et al. (5.17) e quella proposta in questo lavoro (5.16) non ci sia molta differenza. É percettibile un
leggero miglioramento per lunghezze inferiori. Il motivo della congruenza
è imputabile al fatto che la somma del modulo delle dipendenze in temperatura della mobilità di canale lungo γ µ0 e della velocità termica γvth , in
entrambi i casi, assume lo stesso valore pari a 2.
Per verificare la robustezza dei due metodi si fa il medesimo studio,
questa volta tenendo conto anche dello scattering con l’interfaccia ossidosilicio ma continuando a non considerare la degenerazione. Ci si aspetta in
76
LG [nm]
9
18
27
45
90
180
λ0 /lKT0 eq.(5.16)
6.21
4.37
3.26
2.27
1.39
0.60
r0
0.14
0.19
0.24
0.31
0.42
0.63
λ0 /lKT0 eq.(5.17)
4.81
3.50
2.65
1.86
1.13
0.44
rChen0
0.17
0.22
0.27
0.35
0.47
0.69
rM C0
0.14
0.20
0.26
0.35
0.49
0.64
Tabella 5.4: Risultati ottenuti per il dispositivo SOI DG per varie lunghezze
di canale LG , solo scattering fononico. VDS = 0.8 V , VGS = 1.1 V con
densità di carica di inversione al virtual source, a T 0 = 300K, N2D0 =
14.7 × 1012 [#/cm2 ]. Non si considera la degenerazione.
questo caso che la dipendenza dalla temperatura della mobilità di canale
lungo, γµ0 , cambi perchè lo scattering con l’interfaccia è meno sensibile alla
temperatura rispetto allo scattering fononico. Infatti il valore ottenuto per
γµ0 risulta −1.14. Con tale dipendenza ci si aspetta che la formulazione
di Chen et al., che assume semplicemente γ µ0 = −1.5, dia risultati meno
precisi. In tabella 5.5 e 5.6 si riassumono i dati e i risultati ottenuti per
varie lunghezze di canale.
LG [nm]
9
18
27
45
90
180
450
γ µ0
-1.14
-1.14
-1.14
-1.14
-1.14
-1.14
-1.14
γvth
0.4
0.4
0.4
0.4
0.4
0.4
0.4
∆ID /(∆T ID0 ) = α
3.9 × 10−4
0.2 × 10−4
−1.0 × 10−4
−6.1 × 10−4
−1.2 × 10−3
−1.9 × 10−3
−2.8 × 10−3
∆QIN V /(∆T QIN V0 )
9.4 × 10−4
1.0 × 10−3
1.1 × 10−3
1.0 × 10−3
9.6 × 10−4
8.2 × 10−4
7.0 × 10−4
Tabella 5.5: Dati ottenuti per il dispositivo SOI DG per varie lunghezze di
canale LG , VDS = 0.8 V , VGS = 1.1 V con densità di carica di inversione
al virtual source, a T0 = 300K, N2D0 = 14.7 × 1012 [#/cm2 ]. Scattering
fononico e con l’interfaccia. Non si considera la degenerazione.
In figura 5.10 si grafica l’andamento del coefficiente di riflessione. Si
nota che il coefficiente ricavato tenendo conto delle reali dipendenze ha un
andamento più vicino al valore reale ricavato direttamente dalle simulazioni
MC, soprattutto per lunghezze di canale maggiori. Per le lunghezze minori
i valori convergono, ma sono leggermente migliori i risultati ottenuti con
l’espressione ricavata in questo lavoro (5.16). Andando a confrontare i valori dei coefficienti di riflessione nei due casi visti (solo scattering fononico
77
0.8
r
0.6
0.4
0.2
0.0
Da simulazione MC
Da λ/lKT con dipendenze reali [best fit]
Da λ/lKT di Chen et al. [best fit]
0
50
100
LG [nm]
150
200
Figura 5.9: Andamento del coefficiente di riflessione al variare della lunghezza di canale LG . La linea tratteggiata indica il valore reale ricavato dalle
simulazioni MC, triangoli: valori ricavati con le reali dipendenze (eq. 5.16),
cerchi: valori ricavati dall’equazione (5.17). Dispositivo usato SOI DG, doping 1 × 1015 , tox = 0.7 nm, tSi = 12 nm, VDS = 0.8 V , VGS = 1.1 V
con densità di carica di inversione al virtual source, a T 0 = 300K, N2D0 =
14.7 × 1012 [#/cm2 ]. Simulazioni con scattering fononico. Non si considera
la degenerazione
e scattering fononico combinato con scattering all’interfaccia ossido-silicio)
si nota che nel secondo caso r aumenta. La cosa è giustificabile in quanto aggiungendo un meccanismo di scattering si aumenta la probabilità di
collisione e quindi il libero cammino medio λ diminuisce.
Fino ad ora nelle simulazioni effettuate non si è tenuto conto della degenerazione; per completezza si analizza il caso di scattering fononico e con
l’interfaccia tenendo conto della degenerazione. Innanzitutto, verificando
l’andamento al variare della temperatura della mobilità di canale lungo si
trova γµ0 = −1.05. Inoltre si trova che la velocità termica ha una dipendenza dalla temperatura γvth = 0.25 che influenza in modo più significativo
i risultati. In figura 5.11 sono riportati gli andamenti del logaritmo della
velocità termica nel caso degenere e non degenere al variare del logaritmo
della temperatura. Si nota la differenza di pendenza delle due rette interpolanti. Si prevede che a causa della variazione di γ vth l’equazione con le
reali dipendenze (5.16) darà risultati ancora più vicini, rispetto all’equazione
di Chen (5.17), al valore reale. In tabella 5.7 si riportano i dati estratti e in
tabella 5.8 i risultati ottenuti.
In figura 5.12 si riporta l’andamento del coefficiente di riflessione reale ed
78
LG [nm]
9
18
27
45
90
180
450
λ0 /lKT0 eq.(5.16)
3.45
2.43
2.05
1.49
0.94
0.53
0.12
r0
0.23
0.29
0.33
0.40
0.52
0.65
0.89
λ0 /lKT0 eq.(5.17)
4.02
3.04
2.65
2.06
1.48
1.04
0.58
rChen0
0.20
0.25
0.27
0.33
0.40
0.49
0.63
rM C0
0.21
0.32
0.38
0.49
0.63
0.76
0.88
Tabella 5.6: Risultati ottenuti per il dispositivo SOI DG per varie lunghezze
di canale LG , VDS = 0.8 V , VGS = 1.1 V con densità di carica di inversione
al virtual source, a T0 = 300K, N2D0 = 14.7 × 1012 [#/cm2 ]. Scattering
fononico e con l’interfaccia. Non si considera la degenerazione.
LG [nm]
9
18
45
90
180
γ µ0
-1.05
-1.05
-1.05
-1.05
-1.05
γvth
0.25
0.25
0.25
0.25
0.25
∆ID /(∆T ID0 ) = α
1.3 × 10−4
−3.4 × 10−4
−1.0 × 10−3
−1.5 × 10−3
−2.4 × 10−3
∆QIN V /(∆T QIN V0 )
9.4 × 10−4
1.0 × 10−3
1.0 × 10−3
8.8 × 10−4
7.4 × 10−4
Tabella 5.7: Dati ottenuti per il dispositivo SOI DG per varie lunghezze di
canale LG , VDS = 0.8 V , VGS = 1.1 V con densità di carica di inversione
al virtual source, a T0 = 300K, N2D0 = 14.7 × 1012 [#/cm2 ]. Scattering fononico e con l’interfaccia. Effetto della degenerazione incluso nelle
simulazioni.
estratto nei due casi. Si può notare che l’errore commesso con l’espressione
che tiene conto di tutte le dipendenze (5.16) rispetto all’espressione di Chen
(5.17) è minore in questo caso. Il motivo è riconducibile alle dipendenze
sensibilmente diverse rispetto a quelle ipotizzate in [25].
79
0.96
r[]
0.76
0.56
Da simulazione MC
Da λ/lKT con dipendenze reali [best fit]
Da λ/lKT di Chen et al. [best fit]
0.36
0.16
0
100
200
LG [nm]
300
400
500
Figura 5.10: Andamento del coefficiente di riflessione al variare della
lunghezza di canale LG . La linea tratteggiata indica il valore reale ricavato dalle simulazioni MC, triangoli: valori ricavati con le reali dipendenze
(eq. 5.16), cerchi: valori ricavati dall’equazione (5.17). Dispositivo usato
SOI DG, doping 1 × 1015 , tox = 0.7 nm, tSi = 12 nm, VDS = 0.8 V ,
VGS = 1.1 V con densità di carica di inversione al virtual source, a
T0 = 300K, N2D0 = 14.7 × 1012 [#/cm2 ]. Simulazioni con scattering
fononico e scattering all’interfaccia. Non si considera la degenerazione.
log10(vth) [m/s]
5.1
5.05
NON DEG
retta interpolante NON DEG
DEG
retta interpolante DEG
5
2.3
2.4
log10(T) [K]
2.5
2.6
Figura 5.11: Andamento del logaritmo della velocità termica al variare del
logaritmo della temperatura. Nel caso degenere si trova γ vth = 0.25 mentre
nel caso non degenere si era trovato γ vth = 0.4
80
LG [nm]
9
18
45
90
180
λ0 /lKT0 eq.(5.16)
3.27
1.99
1.09
0.70
0.18
r0
0.23
0.34
0.48
0.59
0.85
λ0 /lKT0 eq.(5.17)
3.38
2.44
1.67
1.30
0.77
rChen0
0.23
0.29
0.38
0.44
0.56
rM C0
0.22
0.33
0.51
0.66
0.78
Tabella 5.8: Risultati ottenuti per il dispositivo SOI DG per varie lunghezze
di canale LG , VDS = 0.8 V , VGS = 1.1 V con densità di carica di inversione
al virtual source, a T0 = 300K, N2D0 = 14.7 × 1012 [#/cm2 ]. Scattering fononico e con l’interfaccia. Effetto della degenerazione incluso nelle
simulazioni.
1
Da simulazione MC
Da λ/lKT con dipendenze reali [best fit]
Da λ/lKT di Chen et al. [best fit]
r
0.8
0.6
0.4
0.2
0
50
100
LG [nm]
150
200
Figura 5.12: Andamento del coefficiente di riflessione al variare della
lunghezza di canale LG . La linea tratteggiata indica il valore reale ricavato dalle simulazioni MC, triangoli: valori ricavati con le reali dipendenze
(eq. 5.16), cerchi: valori ricavati dall’equazione (5.17). Dispositivo usato
SOI DG, doping 1 × 1015 , tox = 0.7 nm, tSi = 12 nm, VDS = 0.8 V ,
VGS = 1.1 V con densità di carica di inversione al virtual source, a
T0 = 300K, N2D0 = 14.7 × 1012 [#/cm2 ]. Simulazioni con scattering
fononico e scattering all’interfaccia. Si considera la degenerazione
81
5.3
Simulazione di un dispositivo completo
Il simulatore CoSMOS permette la simulazione di dispositivi reali la cui
soluzione iniziale è stata trovata con un simulatore Drift-Diffusion. I dispositivi utilizzati sono degli SOI DG. In figura 5.13 viene raffigurata la struttura
del dispositivo disegnata mediante il tool grafico ISE-Mdraw. Si possono
axis origin (0,0)
dielectric: tox =0.7nm, ε r =7.0
LG
Source
contact
x
Source
Drain
channel
15
20
p:1x10
n:1x10
20
t Si =6.3nm
n:1x10
Drain contact
Gate contacts
y
Figura 5.13: Raffigurazione schematica del dispositivo simulato. Si possono
distinguere la zona di source e di drain di tipo n con drogaggio 1 × 10 20 e
la zona centrale di tipo p con drogaggio 1 × 10 15 . Lo spessore di silicio del
dispositivo, tSi , è di 12 nm e lo spessore del dielettrico, t ox , è di 1.6 nm,
mentre la sua costante dielettrica relativa è r = 7.0.
distinguere le zone di source e drain con al centro la zona di canale. Le
zone di drain e source hanno un drogaggio di tipo n di 1 × 10 20 mentre la
zona di canale ha un drogaggio di tipo p di 1 × 10 15 . Il simulatore CoSMOS è in grado di leggere le griglie del dispositivo e i profili di doping e
di inizializzare la propria simulazione con una soluzione iniziale fornita dal
simulatore commerciale ISE-Dessis. Per fare questo è necessario descrivere
la mesh nell’input file del simulatore CoSMOS, come visto nel capitolo
3. Un accorgimento per la discretizzazione nell’asse delle x, necessario per
ridurre i tempi di simulazione, è l’infittimento della griglia in prossimità della zona di virtual source. Infatti, essendo questa una zona critica, se venisse
meno una corretta discretizzazione il risultato della simulazione non sarebbe
attendibile. Inoltre infittendo questa zona si ottiene con più precisione la
posizione del virtual source, cosa necessaria in quanto si andranno a valutare
le grandezze necessarie alla determinazione del coefficiente di riflessione proprio in tale punto. In figura 5.14 si raffigura la distribuzione della mesh in
x in relazione all’andamento della prima sottobanda. Il dispositivo dell’esempio è un SOI DG con LG = 20 nm. Si può notare come la griglia venga
notevolmente infittita in prossimità del virtual source, mentre viene lasciata
più lasca in corrispondenza dei contatti di source e drain. In figura 5.15 vengono riportate le prime tre sottobande unprimed e le prime tre sottobande
primed. Si nota che i virtual source di ciascuna sottobanda sono leggermente
82
Eigenvalue [eV]
−0.1
EC(x)
−0.3
−0.5
−0.7
−0.9
−30
−20
−10
0
x [nm]
10
20
30
Figura 5.14: Esempio di mesh in x per un dispositivo con L G = 20 nm. Si
può notare come in prossimità della zona del virtual source la griglia sia più
fitta, mentre in zone meno “critiche” come i contatti sia più lasca.
disallineati tra di loro in x. Tale problema rende di difficile individuazione
il source virtuale in quanto lo si dovrebbe trovare mediando i diversi virtual
source pesati con la popolazione elettronica delle rispettive sottobande. Essendo la variazione di posizione dei virtual source dell’ordine di pochi decimi
di nanometro, si approssima tale posizione con il virtual source della prima
sottobanda, la first unprimed.
Andiamo ora ad estrarre i parametri necessari alla determinazione del coefficiente di riflessione per il dispositivo sopra menzionato con L G = 20 nm.
Le simulazioni sono state eseguite per un intervallo di temperature tra 200K
e 400K. In figura 5.16 riportiamo l’andamento di ∆I D /ID0 . L’andamento
è approssimativamente lineare e l’estrazione della pendenza non è problematica. La pendenza estratta, ∆ID /(∆T ID0 ), è −7.2 × 10−4 . In figura 5.17
riportiamo l’andamento di ∆QIN V /QIN V0 . Si nota che, nonostante una certa dispersione dei valori derivanti dalle simulazioni, si riesce comunque ad
individuare una retta interpolante da cui estrarre la pendenza. La pendenza estratta, ∆QIN V /(∆T QIN V0 ), è −5.1 × 10−4 . In figura 5.18 riportiamo
l’andamento del logaritmo in base dieci della velocità di iniezione al virtual source in funzione del logaritmo in base dieci della temperatura. Dalla
regressione estraiamo γvth = 0.23 Nel caso di dispositivi reali dobbiamo estrarre anche la dipendenza dalla temperatura del KT-layer. Dai dati presenti
in letteratura ci si aspetta un valore γ lKT ≈ 0.7 [14]. In figura 5.19 si riporta
l’andamento del logaritmo decimale del KT-layer al variare del logaritmo
decimale della temperatura. Estraendo la dipendenza di temperatura trovi83
0.4
0.3
Unprimed
Primed (2 subbands)
Eigenvalue [eV]
0.2
0.1
0
−0.1
−0.2
−0.3
−0.4
−20
−15
−10
−5
x [nm]
0
5
10
Figura 5.15: Andamento delle prime tre sottobande unprimed (in continuo)
e le prime tre sottobande (degeneri) primed (in tratteggiato) in prossimità
del virtual source. Si può notare il leggero disallineamento tra i virtual source
delle varie sottobande.
amo γlKT = 0.75. Sono stati simulati, oltre al dispositivo con L G = 20 nm,
anche dispositivi con LG = 30 e 50 nm. In tabella 5.9 si riportano i dati
estratti dalle simulazioni. In tabella 5.10 si riportano i risultati ottenuti
LG [nm]
20
30
50
γ µ0
-1.3
-1.3
-1.3
γvth
0.23
0.15
0.16
γlKT
0.75
0.84
0.86
∆ID /(∆T ID0 ) = α
−7.2 × 10−4
−8.6 × 10−4
−1.0 × 10−3
∆QIN V /(∆T QIN V0 )
−5.1 × 10−4
1.9 × 10−4
4.0 × 10−4
Tabella 5.9: Dati ottenuti per il dispositivo SOI DG con contatti non ideali
per varie lunghezze di canale LG .
applicando l’equazione (5.16) e (5.17). Notiamo sostanzialmente un buon
comportamento di entrambe le equazioni. In figura 5.20 riportiamo l’andamento del coefficiente di riflessione direttamente estratto dalle simulazioni
con quello ottenuto mediante le espressioni (5.16) e (5.17). Si nota che i
coefficienti di riflessione ottenuti mediante l’equazione (5.16) hanno un andamento più congruente con i valori ottenuti direttamente dalle simulazioni.
84
0.1
Da simulazione MC
retta interpolante
∆ID/ID
0
0.05
0
−0.05
−0.1
180
230
280
T [K]
330
380
Figura 5.16: Andamento di ∆ID /ID0 estratto dalle simulazioni (simboli) e
la sua regressione (linea puntinata). La pendenza estratta, ∆I D /(∆T ID0 ),
è −7.2 × 10−4 .
LG [nm]
20
30
50
λ0 /lKT0 eq.(5.16)
6.74
3.54
2.50
r0
0.13
0.22
0.29
λ0 /lKT0 eq.(5.17)
5.14
3.04
2.32
rChen0
0.16
0.25
0.30
rM C0
0.15
0.23
0.33
Tabella 5.10: Risultati ottenuti per il dispositivo SOI DG con contatti non
ideali, per varie lunghezze di canale L G .
85
0.1
Da simulazione MC
retta interpolante
0
∆QINV/QINV [ ]
0.05
0
−0.05
180
230
280
T [K]
330
380
Figura 5.17: Andamento di ∆QIN V /QIN V0 estratto dalle simulazioni
(simboli) e la sua regressione (linea puntinata). La pendenza estratta,
∆QIN V /(∆T QIN V0 ), è −5.1 × 10−4 .
5.2
log10(vth) [m/s]
5.18
5.16
5.14
Da simulazione MC
retta interpolante
5.12
5.1
2.28
2.38
2.48
log10(T) [K]
2.58
2.68
Figura 5.18: Andamento del logaritmo decimale della velocità di iniezione al
variare del logaritmo decimale della temperatura estratto dalle simulazioni
(simboli). Mediante regressione ricaviamo γ vth = 0.23.
86
0.50
log10(lKT) [nm]
0.40
0.30
Da simulazione MC
retta interpolante
0.20
2.28
2.38
2.48
2.58
log10(T) [K]
2.68
Figura 5.19: Andamento del logaritmo decimale del KT-layer al variare del
logaritmo decimale della temperatura estratto dalle simulazioni (simboli).
Mediante regressione ricaviamo γvth = 0.75.
0.4
Da simulazione MC
Da λ/lKT con dipendenze reali [best fit]
Da λ/lKT di Chen et al. [best fit]
0.35
r
0.3
0.25
0.2
0.15
0.1
18
28
LG [nm]
38
48
Figura 5.20: Andamento del coefficiente di riflessione al variare della
lunghezza di canale LG . In puntinato il valore reale ricavato dalle simulazioni MC, triangoli: valori ricavati con le reali dipendenze (eq. 5.16),
cerchi: valori ricavati dall’equazione (5.17). Dispositivo usato SOI DG con
contatti non ideali.
87
88
Capitolo 6
Conclusioni
Con la sempre più spinta riduzione delle dimensioni dei transistori MOS, la
lunghezza di canale dei transistori assume valori comparabili con il libero
cammino medio dei portatori, ed il trasporto nel canale diventa semi-balistico.
Nel capitolo 2 si è studiato l’impatto che il trasporto semi-balistico ha sulla caratterizzazione dei transistori decananometrici. In particolare, abbiamo
osservato che la caratterizzazione della mobilità secondo i metodi tradizionali
produce in realtà una mobilità apparente µ app , diversa dalla mobilità µ0 corrispondente al trasporto uniforme. Più precisamente, la mobilità apparente
dipende dalla lunghezza L del dispositivo e può essere approssimativamente
espressa come:
!−1
=− 1
−1
−1
2
L
(6.1)
µapp = µ0 + µBAL,L
=0
dove µBAL,L è la mobilità balistica per unità di lunghezza ed = α è l’integrale
di Fermi Dirac di ordine α. Mediante il simulatore Monte Carlo descritto
nel capitolo 3 si è potuto simulare il comportamento a bassi campi elettrici
longitudinali dei dispositivi e quindi effettuare una verifica sperimentale di
quanto enunciato nel capitolo 2 riguardo la mobilità apparente. Tali verifiche
sono contenute nel capitolo 4 e confermano il comportamento atteso. Nel
capitolo 4 si è anche effettuato uno studio della mobilità apparente al variare
della temperatura.
Nel capitolo 2 viene anche presentato un metodo per la determinazione
sperimentale del coefficiente di riflessione r, una delle grandezze caratterizzati per il funzionamento del transitore MOS in regime quasi-balistico. Nel
capitolo 5 abbiamo usato il simulatore Monte Carlo per emulare la determinazione del coefficiente di riflessione. Grazie allo studio sulle grandezze
caratterizzanti della corrente del dispositivo è stato possibile fare un’analisi
sulla criticità delle ipotesi su cui il metodo di estrazione si basa. I valori del
coefficiente di riflessione estratti sono stati confrontati con quelli calcolati
dal simulatore in base all’analisi microscopica dei flussi di portatori. Abbiamo potuto cosı̀ verificare l’attendibilità e la robustezza del metodo di es89
trazione. In questo modo si mette in luce un ulteriore utilizzo del simulatore
Monte Carlo, ovvero l’analisi di tecniche di caratterizzazione di dispositivi
decananometrici, ambito in cui i simulatori commerciali basati sul modello
ohmico-diffusio non sono utilizzabili.
90
Bibliografia
[1] Intel Corporation, “Moore’s Law Documents”,
disponibili presso http://www.intel.com/technology/mooreslaw/, ultimo
accesso 19 febbraio, 2007.
[2] G.E. Moore, “Cramming more components onto integrated circuits”,
Electronics, vol. 38, no. 8, April 19, 1965.
[3] G. Ghione, “Dispositivi per la Microelettronica”, MacGraw-Hill, 1998.
[4] M. Lundstrom, “Fundamentals of carrier transport – Second edition”,
Cambridge University Press, 2000.
[5] K. Natori, “Ballistic metal-oxide-semiconductor field effect transistor”,
Journal of Applied Physics, vol. 76, no. 8, October 15, 1994, pp. 48794890.
[6] F. Assad, Z. Ren, S. Datta, and M. Lundstrom, “Performance limits of
silicon MOSFET’s”, IEDM technical Digest, 1999, pp. 21.7.1-21.7.4.
[7] F. Assad, Z. Ren, D. Vasileska, S. Datta, and M. Lundstrom, “On
the performance limits for Si MOSFET’s: a theoretical study”, IEEE
Transactions on electron devices, vol. 47, no. 1, January, 2000, pp. 232240.
[8] M. Lundstrom, “Scattering theory of the short channel MOSFET”,
IEDM technical Digest, 1996, pp. 15.4.1-15.4.4.
[9] M. Lundstrom, “Elementary scattering theory of the Si MOSFET”,
IEEE Electron Device Letters, vol. 18, no. 7, July, 1997, pp. 361-363.
[10] M. Lundstrom, and Z. Ren, “Essential physiscs of carrier transport in
nanoscale MOSFETs”, IEEE Transactions on electron devices, vol. 49,
no. 1, January, 2002, pp. 133-141.
[11] M. Lundstrom, “Device physiscs at the scaling limit: what matters?”,
IEDM technical Digest, 2003, pp. 33.1.1-33.1.4.
91
[12] M. Lundstrom, “On the mobility versus drain current relation for a
nanoscale MOSFET”, IEEE Transactions on electron devices, vol. 22,
no. 6, June, 2001, pp. 293-295.
[13] A. Rahman, J. Guo, S. Datta, and M. Lundstrom, “Theory of ballistic
nanotransistors”, IEEE Transaction on Electron Devices, vol. 50, no. 9,
September, 2003, pp. 1853-1864.
[14] A. Rahman, M. Lundstrom, “A compact scattering model for the
nanoscale Double-Gate MOSFET”, IEEE Transaction on Electron
Devices, vol. 49, no. 3, March, 2002, pp. 481-489.
[15] J. Wang, and M. Lundstrom, “Ballistic Transport in high electron mobility transistor”, IEEE Transactions on Electron Devices, vol. 50, no. 7,
July, 2003, pp. 1604-1609.
[16] J. Wang, and M. Lundstrom, “Corrections to “Ballistic Transport in
high electron mobility transistor” ”, IEEE Transactions on Electron
Devices, vol. 50, no. 10, October, 2003, p. 2185.
[17] M.S. Shur “Low ballistic mobility in submicron HEMTs”, IEEE
Transactions on Electron Devices, vol. 23, no. 9, September, 2002,
pp. 511-513.
[18] A. Lochtefeld, and D.A. Antoniadis “On experimental determination
of carrier velocity in deeply scaled NMOS: how close to the thermal limit?”, IEEE Transactions on Electron Devices, vol. 22, no. 2,
February, 2001, pp. 95-97.
[19] G. Baccarani, and S. Reggiani “A compact double-gate MOSFET
model comprising quantum-mechanical and nonstatic effects ”, IEEE
Transactions on Electron Devices, vol. 46, no. 8, August, 1999,
pp. 1656-1666.
[20] R. Clerc, P. Palestri, and L. Selmi “On the physical understanding of the
kT/layer concept in quasi-ballistic regime of transport in nanoscale devices”, IEEE Transaction on Electron Devices, vol. 53, no. 7, July, 2006,
pp. 1634-1640.
[21] F. Andrieu, T. Ernst, O. Rozeau, Y. Bogumilowicz, J.-M. Hartmann,
L. Brèvard, A. Toffoli, D. Lafond, H. Danas, B. Ghyselen, F. Fournel, G. Ghibaudo, and S. Deleonibus “In-depth study of strained
SGOI nMOSFETs down to 30nm gate length”, IEEE Proceeding of
ESSDERC, Grenoble, France, 2005, pp. 297-299.
[22] F. Lime, F. Andrieu, J. Derix, G. Ghibaudo, F. Bofeou, and T. Skotnicki “Low temperature characterization of effective mobility in uniax92
ial and biaxial strained N-MOSFET”, IEEE Proceeding of ESSDERC,
Grenoble, France, 2005, pp. 525-528.
[23] W. Chaisantikulwat, M. Mous, G. Ghibaudo, C. Gallon, C. FenouilletBeranger, D.K. Maude, T. Skotnicki and S. Cristoloveanu “Magnetoresistance technique for mobility extraction in short channel FDSOI
transistors”, IEEE Proceeding of ESSDERC, Grenoble, France, 2005,
pp. 569-572.
[24] J. Lusakowskj, W. Knap, Y. Meziani, J.-P. Cesso, A. El Fatimy,
R. Tauk, N. Dyakonova, G. Ghibaudo, F. Boeuf and T. Skotnicki
“Influence of ballistic and pocket effects on electron mobility in Si
MOSFETs”, IEEE Proceeding of ESSDERC, Grenoble, France, 2005,
pp. 561-564.
[25] M.-J. Chen, H.-T. Huang, K.-C. Huang, P.-N. Chen, C.-S. Chang, and
C.H. Diaz “Temperature dependent channel backscattering coefficients
in nanoscale MOSFETs”, IEDM technical Digest, December, 2002,
pp. 39-42.
[26] K.-W. Ang, H.-C. Chin, K.-J. Chui, M.-F. Li, G. Samadura, and Y.C. Yeo “Carrier backscattering characteristics of strained N-MOSFET
featuring silicon-carbon source/drain regions”, IEEE Transaction on
Electron Devices, vol. 53, no. 7, July, 2006, pp. 89-92.
[27] M.-J. Chen, S.-G. Yan, R.-T. Chen, C.-Y. Hsieh, P.W. Huang, and H.P. Chen “Temperature-oriented experiment and simulation as corroborating evidence of MOSFET backscattering theory”, IEEE Transaction
on Electron Devices, vol. 28, no. 2, February, 2007, pp. 177-179.
[28] F. Stern, and W.E. Howard “Properties of semiconductor surface inversion layer in the electric quantum limit”, Physical Review, vol. 163,
no. 3, 1967, pp. 816-835.
[29] S. Takagi, A. Toriumi, M. Iwase, and H. Tango, “On the universality of inversion layer mobility in Si MOSFET’s: Part I – Effects
of substrate impurity concentration”, IEEE Transactions on Electron
Devices, vol. 41, no. 12, December, 1994, pp. 2357-2362.
[30] S. Takagi, A. Toriumi, M. Iwase, and H. Tango, “On the universality of
inversion layer mobility in Si MOSFET’s: Part II – Effects of surface
orientation”, IEEE Transactions on Electron Devices, vol. 41, no. 12,
December, 1994, pp. 2363-2368.
[31] P.R. Chidambaram, C. Bowen, S. Chakravarthi, C. Machala and
R. Wise “Foundamentals of silicon material properties for successful
exploitation of strain engineering in modern CMOS manufacturing”,
93
IEEE Transactions on Electron Devices, vol. 53, no. 5, May, 2006,
pp. 944-964.
[32] S.E. Thompson, G. Sun, Y. Sung, and T. Nishida “Uniaxalprocess-induced strained-Si: extending the CMOS roadmap”, IEEE
Transactions on Electron Devices, vol. 53, no. 5, May, 2006,
pp. 1010-1020.
[33] L. Lucci, “CoSMOS user manual”, ottenibile dalla rete picolit.diegm.uniud.it nella directory /home/cop/COSMOS/doc, solo per
utenti autorizzati, April 2006.
[34] L. Lucci, P. Palestri, D. Esseni, and L. Selmi, “Multi-subband Monte
Carlo modeling of nano-MOSFETs with strong vertical quantization
and electron gas degeneration”, IEDM Technical Digest, December 57, 2005, pp. 617-620.
[35] J.S. Blakemore, “Approximations for Fermi-Dirac integrals especially the function = 1 (η) used to describe electron density in a
2
semiconductor”, Solid-State Electronics, vol. 25, no. 11,
1982,
pp. 1067-1076.
[36] P. Van Halen, and D.L. Pulfrey “Accurate, short series approximations
to Fermi-Dirac integrals of order -1/2, 1/2, 1, 3/2, 2, 5/2, 3, and 7/2”,
J. Appl. Phys, vol. 57, no. 11, June 15, 1982, pp. 5271-5274.
94
Ringraziamenti
Finalmente è arrivato il capitolo dei ringraziamenti.
Un grazie sentito va innanzitutto al prof. David Esseni per avermi seguito
scrupolosamente e con pazienza durante tutta la durata del periodo di tesi.
Un grazie al prof. Pierpaolo Palestri, sempre disponibile a dare spiegazioni
e consigli. Un grazie anche al prof. Luca Selmi che nonostante gli impegni
è sempre stato presente. Grazie anche ai dottorandi di microelettronica per
i molti consigli ricevuti.
Ringrazio la mia famiglia: i miei genitori, per non avermi mai fatto mancare
nulla, in tutti i sensi, e i nonni, per l’incoraggiamento continuo. “Last but
not least”, grazie a Monica, per essermi stata sempre vicino.
95