La teoria del consumo
Il surplus del consumatore
e
la domanda di mercato.
Mario Sportelli
Dipartimento di Matematica
Università degli Studi di Bari
Via E. Orabona, 4
I-70125 Bari (Italy)
(Tel.: +39 (0)99 7720 626; fax: +39 (0)99 7763 295)
E-mail: [email protected]
URL: http://www.dm.uniba.it/~msportelli
Il surplus del consumatore.
Definizione: Il surplus del consumatore è una misura
monetaria del benessere associato alla quantità
consumata di un bene.
Per misurare il benessere relativo al consumo di un bene x, si
utilizza una funzione di utilità che include il bene x e un bene
composito y:
u = u ( x, y )
Definizione: Per bene composito si intende l’ammontare di
moneta destinato all’acquisto di tutti i beni inclusi nel paniere
di consumo diversi da x.
2
Il surplus del consumatore.
Osservazione: Se y è un ammontare di moneta il suo prezzo
sarà uguale a 1, perché un’unità di moneta si scambia sempre
con una unità di moneta.
Il problema di massimizzazione dell’utilità da risolvere è,
pertanto, il seguente:
max u( x, y )
sub. =
m px x + y
da cui deduciamo,
ux
=
−
=
− px
MRS
uy
=
m px x + y
3
Il surplus del consumatore.
Risolvendo il sistema di scelta
ottima, otteniamo la funzione di
domanda
x( px , m)
Osservazione: Fino a quando non
diviene noto il prezzo px , la
funzione di domanda denota le
quantità che il consumatore è
disposto ad acquistare ai diversi
prezzi.
Nel momento in cui l’informazione sul
prezzo è acquisita (px = px ), la funzione di
domanda determina x* .
4
Il surplus del consumatore.
A partire dalla scelta x* (che, per ipotesi,
include n unità di bene), supponiamo di
sottrarre al consumatore una unità di
bene ∆x. Ciò provocherà una riduzione
del suo benessere. Tuttavia, se
compensiamo il consumatore con una
quantità addizionale dell’altro bene, il
suo benessere resterà invariato.
Per stabilire in che misura dobbiamo
compensarlo, utilizziamo il MRS:
∆y
u
MRS = =
− x =
− px
uy
∆x
da cui deduciamo che
∆y =− p x ∆x > 0
perché ∆x < 0.
5
Il surplus del consumatore.
Quando ∆x = –1, al consumatore
rimborseremo esattamente il prezzo di
mercato p per la prima unità sottratta di
bene.
Se, a partire da (x –1) sottraiamo un’altra
unità, il prezzo che dovremo rimborsare non
è più il prezzo di mercato, ma un prezzo di
riserva.
Definizione: Il prezzo di riserva economicamente denota la disponibilità marginale a
pagare, ossia quanto il consumatore è
disposto a pagare per una unità di bene.
(NB – Il prezzo di riserva non ha alcun legame con il prezzo di
mercato, ma dipende dall’importanza relativa che l’individuo
attribuisce al bene).
Con lo stesso procedimento, ossia
compensando sempre il consumatore con
quantità addizionali di y, possiamo sottrarre
altre unità di x fino ad azzerarne il consumo.
6
Il surplus del consumatore.
Se il consumatore è stato sempre compensato con successive quantità addizionali di
moneta, il suo benessere non ha subito variazioni. Pertanto, possiamo interpretare
l’ammontare complessivo di moneta che gli abbiamo fornito come il valore
(soggettivo) che egli attribuisce alle n unità x* di bene che aveva acquistato. Tale
valore, dal punto di vista economico, misura la disponibilità totale a pagare per
ottenere la quantità x*.
La disponibilità totale a pagare è interpretata dagli economisti come una misura
monetaria dell’utilità totale associata alla quantità x* del bene.
Per misurare la disponibilità totale a pagare, ossia l’utilità totale in termini monetari,
dobbiamo semplicemente sommare i prezzi di riserva di ciascuna unità, cioè le somme
che abbiamo rimborsato al consumatore per compensarlo della perdita delle diverse
unità di bene:
utilità totale
=
di x*
n
∑ p ( x )∆x
i =0
r
i
i
dove ∆xi = 1 (per ipotesi).
7
Il surplus del consumatore.
Osservazione: Con riferimento al grafico
della domanda di x, la somma che
abbiamo determinato altro non è che la
somma delle n ordinate.
Se ∆x → 0, ossia se la variazione ∆x
diviene molto piccola (infinitesima), allora,
l’insieme delle ordinate si infittisce e
ricopre interamente l’area sotto la curva di
domanda.
Vale, pertanto, la seguente:
x
n
lim
∆x → 0
(τ )dτ
x ) ∆x ∫ p =
∑ p (=
i =0
r
i
i
r
area A
0
8
Il surplus del consumatore.
Definizione 1: Per surplus lordo del consumatore
si intende l’utilità totale in termini monetari
associata alla quantità acquistata di un bene.
Il surplus lordo è un modo alternativo per
indicare la “disponibilità totale a pagare”.
La “disponibilità marginale a pagare” è un
modo alternativo per indicare il “prezzo di
riserva”.
Gli economisti interpretano il “prezzo di
riserva” come una misura monetaria
dell’utilità marginale.
Definizione 2: Per surplus netto del consumatore
si intende la differenza tra ciò che il
consumatore sarebbe disposto a spendere per
x* e ciò che effettivamente spende:
x
Surplus netto consumatore
= CS
=
∫ p (τ )dτ − px *
r
0
9
Il surplus del consumatore
Osservazione 1: Per una generica funzione di utilità non c’è una
perfetta corrispondenza tra prezzo di riserva e utilità marginale.
Tuttavia convenzionalmente, gli economisti assumono che il
prezzo di riserva sia una buona approssimazione dell’utilità
marginale.
Osservazione 2: Una univoca corrispondenza tra utilità marginale
e prezzo di riserva è verificata solo per la funzione di utilità quasi
lineare.
Sia=
u v ( x ) + y una generica funzione di utilità quasi lineare.
La scelta ottima segue dalla soluzione del seguente sistema:
−u x =
−v′( x ) =
− px
MRS =
m px x + y
=
10
I coefficienti di elasticità della domanda individuale.
Sia xi(p, m) una funzione di domanda individuale del bene i.
La sensibilità di xi al variare dei prezzi e del reddito è misurata
convenzionalmente con i coefficienti di elasticità.
Definizione: Per coefficiente di elasticità di una funzione s’intende il
rapporto tra la variazione relativa o percentuale della variabile
dipendente e la variazione relativa o percentuale di una variabile
indipendente.
Con riferimento alla funzione di domanda possiamo calcolare tre
coefficienti di elasticità:
a) l’elasticità al prezzo pi ;
b) l’elasticità al prezzo di un qualunque altro bene pj (elasticità incrociata).
c) L’elasticità al reddito.
11
L’elasticità al prezzo pi
∆xi % ∆xi ∆pi ∆xi pi
:
ε pi =
=
=
0
xi
pi
∆pi %
∆pi xi
Questo coefficiente di elasticità è sempre negativo per i beni normali o
inferiori ordinari e positivo per i beni inferiori di Giffen.
Convenzionalmente, per i beni normali l’interpretazione è fatta con
riferimento al valore assoluto. Pertanto:
ε p 1
i
Elasticità maggiore di 1: la domanda si dice elastica (data una variazione
del prezzo, la quantità varia in misura più che proporzionale).
Elasticità minore di 1: la domanda si dice anelastica o rigida (data una
variazione del prezzo, la quantità varia in misura meno che
proporzionale).
Elasticità uguale a 1: prezzo e quantità variano proporzionalmente.
12
L’elasticità al prezzo pj
∆xi % ∆xi ∆p j ∆xi p j
=
=
0
ε pi =
:
∆p j %
xi
pj
∆p j xi
Questo coefficiente di elasticità è positivo se i beni sono succedanei e
negativo per i beni complementari. Trattandosi comunque di un
rapporto, il suo valore con segno o assoluto è sempre tale che
ε p 1
j
e misura il grado di succedaneità o complementarietà.
Elasticità maggiore di 1: data una variazione del prezzo, la quantità varia
in misura più che proporzionale.
Elasticità minore di 1: data una variazione del prezzo, la quantità varia in
misura meno che proporzionale.
Elasticità uguale a 1: prezzo e quantità variano proporzionalmente.
13
L’elasticità al reddito m.
∆xi % ∆xi ∆m ∆xi m
:
εm =
=
=
0
xi m
∆m %
∆m xi
Questo coefficiente di elasticità è positivo se il bene è normale, negativo
se il bene è inferiore. Trattandosi comunque di un rapporto, il suo valore
è sempre tale che
εm 1
e misura il grado di normalità o inferiorità del bene.
Elasticità maggiore di 1: data una variazione del reddito, la quantità
varia in misura più che proporzionale.
Elasticità minore di 1: data una variazione del reddito, la quantità varia
in misura meno che proporzionale.
Elasticità uguale a 1: reddito e quantità variano proporzionalmente.
14
Dalla domanda individuale alla domanda di mercato.
Supponiamo che nel mercato ci siano m consumatori che acquistano il
bene xi . Fissati i redditi e i prezzi di tutti gli altri beni diversi da xi ,
possiamo sommare tutte le quantità acquistate in corrispondenza dei
diversi possibili prezzi pi . Questa operazione consente di determinare la
domanda di mercato del bene xi . Possiamo indicare con Q(p) oppure
Y(p) la domanda di mercato:
m
Q( p ) = ∑ xij ( pi )
j =1
La domanda di mercato è generalmente inclinata negativamente.
Osservazione: Poiché i prezzi degli altri beni diversi da xi ed i redditi
contribuiscono a definire i parametri della funzione Q(p), le loro
possibili variazioni trasporranno nel piano la funzione a parità di prezzo.
15
Elasticità della domanda di mercato.
Il coefficiente di elasticità della domanda
di mercato va interpretato come quello
relativo alla domanda individuale:
domanda elastica
∆Q % ∆Q ∆p ∆Q p
:
ε
=
=
=
1 domanda proporzionale
Q
p
∆p %
∆p Q
domanda anelastica
Osservazione 1: Su una domanda lineare
l’elasticità cambia da punto a punto. Ciò
accade perché, sebbene sia costante il
coefficiente angolare (la pendenza),
cambia il rapporto p/q. Pertanto:
ε ∈ [∞, 0]
Osservazione 2: Se vogliamo far
dipendere l’elasticità dalla pendenza,
dobbiamo fissare un rapporto p/q.
16
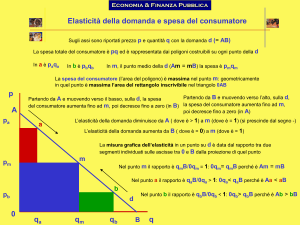
Elasticità della domanda di mercato.
17
Funzione di domanda con elasticità costante.
Il parametro b denota l’elasticità:
Q = ap
−b
18
Elasticità e spesa dei consumatori.
La spesa dei consumatori è determinata dal prodotto tra prezzo di
mercato e quantità acquistata:
=
S pQ
= pQ ( p )
o Osservazione 1: Analiticamente la spesa è un prodotto di funzioni:
la funzione p e la funzione Q(p).
o Osservazione 2: La spesa dei consumatori coincide con i ricavi
delle imprese (R).
Le variazioni della spesa (come quelle dei ricavi) sono
determinate dal seguente tasso di variazione:
dQ p
dS
dQ
=
=
Q( p) + p
Q 1 +
Q(1 − ε ) 0
=
dp
dp
dp Q
19