LA LEZIONE
Potenziale ed energia potenziale
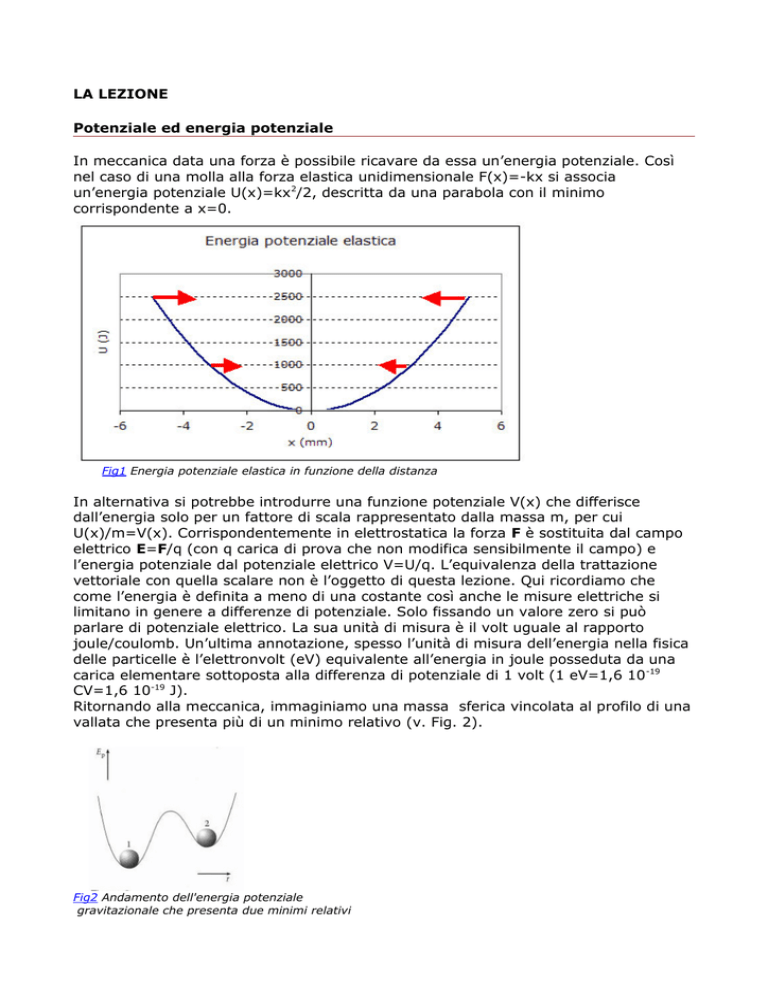
In meccanica data una forza è possibile ricavare da essa un’energia potenziale. Così
nel caso di una molla alla forza elastica unidimensionale F(x)=-kx si associa
un’energia potenziale U(x)=kx2/2, descritta da una parabola con il minimo
corrispondente a x=0.
Fig1 Energia potenziale elastica in funzione della distanza
In alternativa si potrebbe introdurre una funzione potenziale V(x) che differisce
dall’energia solo per un fattore di scala rappresentato dalla massa m, per cui
U(x)/m=V(x). Corrispondentemente in elettrostatica la forza F è sostituita dal campo
elettrico E=F/q (con q carica di prova che non modifica sensibilmente il campo) e
l’energia potenziale dal potenziale elettrico V=U/q. L’equivalenza della trattazione
vettoriale con quella scalare non è l’oggetto di questa lezione. Qui ricordiamo che
come l’energia è definita a meno di una costante così anche le misure elettriche si
limitano in genere a differenze di potenziale. Solo fissando un valore zero si può
parlare di potenziale elettrico. La sua unità di misura è il volt uguale al rapporto
joule/coulomb. Un’ultima annotazione, spesso l’unità di misura dell’energia nella fisica
delle particelle è l’elettronvolt (eV) equivalente all’energia in joule posseduta da una
carica elementare sottoposta alla differenza di potenziale di 1 volt (1 eV=1,6 10 -19
CV=1,6 10-19 J).
Ritornando alla meccanica, immaginiamo una massa sferica vincolata al profilo di una
vallata che presenta più di un minimo relativo (v. Fig. 2).
Fig2 Andamento dell'energia potenziale
gravitazionale che presenta due minimi relativi
Senza attrito la sferetta oscilla tra due posizioni estreme aventi pari energia potenziale
gravitazionale. Considerando invece l’attrito, le buche di potenziale (i minimi relativi)
rappresentano le due possibili soluzioni raggiungibili dal sistema dopo un tempo
sufficientemente lungo. Prendiamo ora in considerazione quale sia la condizione per
una pallina, situata in prossimità del minimo nella parte sinistra della guida, di riuscire
a superare la barriera di potenziale costituita dalla collinetta (il massimo relativo) del
profilo. La risposta è assai semplice: l’energia cinetica della pallina deve compensare
la differenza dell’energia potenziale gravitazionale tra il massimo e la posizione
iniziale. L’equivalente elettrodinamico della situazione precedente può essere
rappresentato da due metalli separati da un sottilissimo strato di un diverso materiale.
Fig3 Giunzione formata da due conduttori separati da un
sottilissimo strato di un diverso materiale
Un singolo elettrone di conduzione del metallo avente un’energia E trova una barriera
di potenziale nello strato interposto tra i due metalli. Dal punto di vista classico,
l’elettrone è confinato in una delle due parti metalliche se la sua energia E non è
superiore all’energia potenziale della barriera. Dal punto di vista della meccanica
quantistica, la particella è sostituita da un’onda che oltre a essere riflessa dalla
barriera è trasmessa attraverso di essa. Prendiamo come riferimento la simulazione di
Fig4, se lo spessore è pari a 64 nanometri e le due energie differiscono di -1,7 eV la
particella non ha alcuna possibilità di oltrepassare l’ostacolo. Viceversa, mantenendo
le stesse energie e dimezzando lo spessore della barriera, il pacchetto d’onda ha una
probabilità non nulla di attraversarla.
Fig4 A sinistra, l’energia del pacchetto d’onda e lo spessore elevato della barriera non permettono
l’attraversamento della barriera; a destra, con uno spessore inferiore, si realizza l’effetto tunnel
Fig5 Microscopio STM
La capacità di una particella quantistica di andare oltre barriere di energia potenziale
in apparente violazione del principio di conservazione dell’energia è chiamata effetto
tunnel (quantum tunneling) per evidenziare il passaggio che avviene a un livello più
basso di energia seguendo un percorso non ammissibile nella meccanica classica per
le singole particelle.1
Il principio di Heisenberg che stabilisce (per le variabili coniugate energia e tempo)
un’indeterminazione nel valore dell’energia è il fondamento del fenomeno quantistico.
In ambito semiclassico l’effetto tunnel è stato anche interpretato in termini di scambi
energetici tra il sistema quantistico e l’apparato di misura.
L’effetto tunnel oltre a spiegare importanti fenomeni fisici (decadimento alfa) è alla
base di applicazioni come il microscopio a scansione per effetto tunnel (STM) che
ricostruisce la superficie di un campione con dimensioni prossime a quelle delle
dimensioni atomiche. Gerd Binnig e Heinrich Rohrer dell’IBM di Zurigo ricevettero per
l’invenzione del microscopio STM il premio Nobel per la fisica nel 1986.
Superconduttività nei metalli
I portatori di carica nei metalli sono particolari elettroni, detti di conduzione, che non
sono legati ai singoli atomi del reticolo. Gli elettroni liberi si muovono ordinatamente
sotto l’azione di un campo elettrico (una differenza di potenziale applicata agli estremi
del conduttore) e trova nelle vibrazioni degli atomi un ostacolo che è misurabile
macroscopicamente come resistività del conduttore al passaggio della corrente.
Fig6 Elettroni di conduzione
All’abbassarsi della temperatura la resistività del metallo diminuisce quasi linearmente
fino a crollare a valori trascurabili per temperature minori di un valore critico T C
dell’ordine dei kelvin (con un salto anche di 1012 nel valore della resistività).
Fig7 Andamento della resistività elettrica in funzione della temperatura nel caso di conduttori normali
(curva a) e di superconduttori (curva b)
Fig8 Coppie di Cooper: a temperature estremamente basse un elettrone può modificare il reticolo
cristallino creando una zona con una densità di carica positiva maggiore che attrae una seconda carica
negativa
La scoperta nel 1911 della superconduzione dei metalli, che valse a Heike Kamerlingh
Onnes il premio Nobel della fisica nel 1913, fu per molti decenni un enigma. Solo nel
1957 Leon N. Cooper, John Bardeen e John R. Schrieffer proposero una teoria
1
Una simulazione di dinamica molecolare classica a molte particelle in una buca di potenziale (tutte con
energia più bassa rispetto a quella della barriera) può portare a una probabilità non nulla di superamento
della barriera da parte di alcune particelle che, attraverso urti, acquistano energia sufficiente dalle altre.
microscopica del fenomeno. In essa, il comportamento collettivo degli elettroni
(inspiegabile per particelle che non possono avere lo stesso stato) era ricondotto a un
accoppiamento degli stessi (coppie di Cooper). Nei metalli, al di sotto della
temperatura critica, l’interazione tra un elettrone e un gruppi di ioni comporta una
distorsione del reticolo che esercita su un secondo elettrone un debole accoppiamento.
Gli elettroni a coppie si comportano come singole particelle (bosoni) che possono
coesistere tutte nello stesso stato e possono muoversi nel materiale senza risentire
degli effetti delle perdite di energia tipiche dei conduttori normali.
Nel 1972, ai tre autori citati per la teoria della superconduttività, oggi denominata con
le iniziali BCS, fu assegnato il premio Nobel per la fisica. L’anno successivo seguì il
premio Nobel per l’effetto tunnel tra superconduttori previsto da Brian D. Josephson e
verificato da Ivar Giaever e Leo Esaki. L’intuizione del giovane fisico gallese fu quella
di immaginare (molto prima di una realizzazione pratica) una sottilissima barriera di
dielettrico (1 nm) che non impediva a due superconduttori di trasmettere attraverso la
barriera di potenziale dell’isolante le coppie di elettroni. L’ordine a grande distanza
delle coppie di elettroni (quasi particelle) mantiene una supecorrente senza caduta di
tensione ai capi della giunzione costituendo l’effetto Josephson in corrente continua.
Fig9 Giunzione Josephson e coppie di Cooper
La differenza di potenziale standard
Il sistema di due superconduttori separati da un sottilissimo strato di ossido
(giunzione Josephson) che consente il passaggio alle coppie di Cooper (comportandosi
come un unico superconduttore), mostra un secondo effetto quando vi è una tensione
diversa da zero alle estremità dei due superconduttori.
Fig10 Effetto Josephson
Fig11 Curva caratteristica di una giunzione Josephson alla temperatura di 6,5 K
In tal caso si produce una corrente alternata di frequenza f che soddisfa la relazione
tra energie: hf=2eV. Il rapporto tra frequenza e tensione è allora uguale al doppio
della carica elementare divisa la costante di Planck: f/V=2e/h. La verifica dell’effetto
Josephson in corrente alternata si può realizzare indirettamente sottoponendo la
giunzione a una radiazione di frequenza f e osservando i salti della corrente nella
curva caratteristica (tensione-corrente) corrispondenti ai valori di tensione V n=nhf/2e.
L’effetto Josephson permette quindi di misurare la costante omonima K J=2e/h;
oppure, rovesciando il ragionamento, fissando il valore di K J, è possibile ricondurre lo
standard di tensione alla misura di una frequenza. Il Comitato Internazionale dei pesi
e delle misure, durante la XVII Conferenza Generale, ha approvato per la costante di
Josephson il valore di 483597,9 GHz/V, ovvero ha definito il rapporto tra la frequenza
e la differenza di potenziale elettrico corrispondente al valore n=1 per una giunzione
Josephson irradiata da una radiazione elettromagnetica di frequenza f. Ha stabilito
così che l’effetto Josephson, insieme al valore della costante, possa essere utilizzato
per stabilire un riferimento standard per la forza elettromotrice avente una incertezza
(deviazione standard) per il volt pari a 4 parti su 107. Il valore 483597,9 GHz/V è da
allora contrassegnato dal simbolo KJ-90 per indicare la data del primo gennaio 1990
come inizio della nuova definizione del campione pratico: V=f/KJ-90. Ancora oggi una
differenza di potenziale x volte l’unità pratica standard equivale a quella misurabile ai
capi di una giunzione Josephson irradiata da un’onda elettromagnetica monocromatica
di frequenza x/483597,9 109.