1 ELEMENTI DI PSICROMETRIA

Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
1 ELEMENTI DI PSICROMETRIA
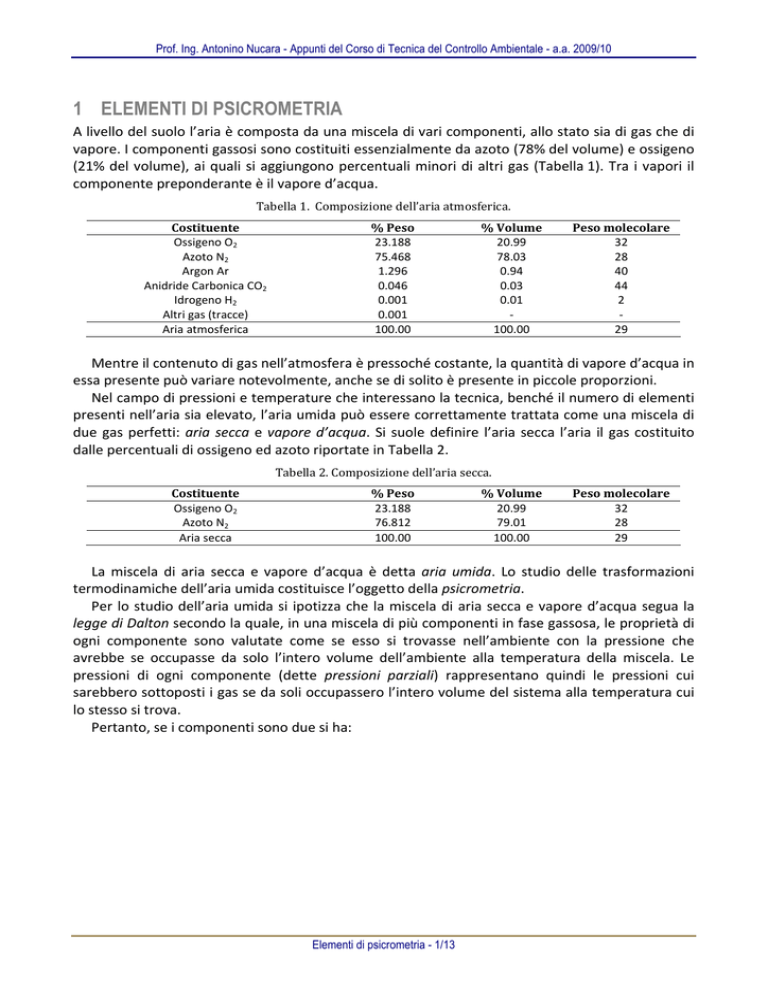
A livello del suolo l’aria è composta da una miscela di vari componenti, allo stato sia di gas che di vapore. I componenti gassosi sono costituiti essenzialmente da azoto (78% del volume) e ossigeno (21% del volume), ai quali si aggiungono percentuali minori di altri gas (Tabella 1). Tra i vapori il componente preponderante è il vapore d’acqua. Tabella 1. Composizione dell’aria atmosferica. Costituente Ossigeno O2 Azoto N2 Argon Ar Anidride Carbonica CO2 Idrogeno H2 Altri gas (tracce) Aria atmosferica % Peso 23.188 75.468 1.296 0.046 0.001 0.001 100.00 % Volume 20.99 78.03 0.94 0.03 0.01 ‐ 100.00 Peso molecolare 32 28 40 44 2 ‐ 29 Mentre il contenuto di gas nell’atmosfera è pressoché costante, la quantità di vapore d’acqua in essa presente può variare notevolmente, anche se di solito è presente in piccole proporzioni. Nel campo di pressioni e temperature che interessano la tecnica, benché il numero di elementi presenti nell’aria sia elevato, l’aria umida può essere correttamente trattata come una miscela di due gas perfetti: aria secca e vapore d’acqua. Si suole definire l’aria secca l’aria il gas costituito dalle percentuali di ossigeno ed azoto riportate in Tabella 2. Tabella 2. Composizione dell’aria secca. Costituente Ossigeno O2 Azoto N2 Aria secca % Peso 23.188 76.812 100.00 % Volume 20.99 79.01 100.00 Peso molecolare 32 28 29 La miscela di aria secca e vapore d’acqua è detta aria umida. Lo studio delle trasformazioni termodinamiche dell’aria umida costituisce l’oggetto della psicrometria. Per lo studio dell’aria umida si ipotizza che la miscela di aria secca e vapore d’acqua segua la legge di Dalton secondo la quale, in una miscela di più componenti in fase gassosa, le proprietà di ogni componente sono valutate come se esso si trovasse nell’ambiente con la pressione che avrebbe se occupasse da solo l’intero volume dell’ambiente alla temperatura della miscela. Le pressioni di ogni componente (dette pressioni parziali) rappresentano quindi le pressioni cui sarebbero sottoposti i gas se da soli occupassero l’intero volume del sistema alla temperatura cui lo stesso si trova. Pertanto, se i componenti sono due si ha: Elementi di psicrometria - 1/13
Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
Gas A
Pressione, pA
Volume, V
Temperatura, T
Miscela (Gas A + Gas B)
Pressione, p
Volume, V
Temperatura, T
Gas B
Pressione, pB
Volume, V
Temperatura, T
Dall’equazione di stato per la miscela e per i singoli gas è possibile scrivere: pV = nRT
p AV = n A RT p B V = nB RT
Essendo n = n A + n B , ricavando dalle tre equazioni il numero di moli si ha: pV p AV p B V
=
+
RT RT
RT
e quindi: p = p A + pB (1) La pressione totale della miscela è quindi pari alla somma delle pressioni parziali dei singoli componenti. La somma delle pressioni parziali dell’aria secca e del vapore d’acqua, ossia la pressione totale, è la pressione atmosferica. La pressione parziale del vapore è variabile a seconda delle condizioni; essa può assumere tutti i valori compresi tra 0 ed il valore della pressione di saturazione alla temperatura della miscela: in quest’ultimo caso l’aria è detta satura. A partire da tali condizioni di saturazione, se si tenta di mettere altro vapore d’acqua nella miscela esso condenserà, raccogliendosi in gocce e separandosi dalla fase aeriforme. Se per lo studio delle miscele si utilizza il modello di Dalton, è possibile dimostrare, per mezzo di una semplice esperienza, che l’energia interna, l’entalpia e l’entropia godono della proprietà additiva. Pertanto si ha: U = ∑U i = ∑ ni ui = ∑ M i ui
i
i
i
H = ∑ H i = ∑ ni hi = ∑ M i hi i
i
(2) i
S = ∑ S i = ∑ ni s i = ∑ M i s i
i
i
i
essendo ni ed Mi rispettivamente il numero di moli e la massa dell’i‐esimo componente. 1.1 Composizione della miscela
Dalla regola delle fasi, lo stato fisico di un sistema costituito da due componenti ed una fase è descritto da tre coordinate termodinamiche. Usualmente si utilizzano la temperatura e la Elementi di psicrometria - 2/13
Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
pressione della miscela ed uno tra i diversi parametri che ne definiscono la composizione. Per la particolare proprietà dell’aria secca di mantenere la sua massa costante è opportuno riferire tutte le proprietà fisiche della miscela alla massa d’aria secca contenuta. Per individuare il contenuto di umidità nella miscela vengono allora introdotte alcune grandezze e precisamente il titolo, l’umidità relativa ed il grado di saturazione. 1.1.1 Titolo
Il titolo o umidità specifica o rapporto di miscela è il rapporto fra la massa di vapore d’acqua e quella di aria secca presenti in un determinato volume V di una miscela che si trova alla temperatura T. ⎛M
x = ⎜⎜ v
⎝ Ma
⎞
⎟⎟ ⎠ V ,T
(3) Il titolo è facilmente riconducibile ad un rapporto di pressioni parziali pv e pa. Utilizzando l’equazione di stato ed ipotizzando l’aria secca come un gas biatomico di peso molecolare 29, si ottiene infatti: Mv
pV
pV
RT ⇒ M v = (PM )v v = 18 v
(PM )v
RT
RT
Ma
paV
p aV
aria secca paV = na RT ⇒ p aV =
RT ⇒ M a = (PM )a
= 29
(PM )a
RT
RT
vapore
pv V = nv RT ⇒ pv V =
da cui si ha: x=
M v 18p v
p
=
= 0 ,622 v M a 29 p a
pa
(4) Il titolo viene espresso in kg oppure in g di vapore per kg di aria secca. Il suo valore può variare tra 0 ed un valore massimo dipendente dalla temperatura, corrispondente alle condizioni di saturazione. 1.1.2 Umidità relativa
L’umidità relativa o grado igrometrico, è definita come il rapporto fra la massa di vapore contenuta nel volume V alla temperatura T e la massa di vapore che si avrebbe in condizioni di saturazione alla stessa temperatura: ⎛M
ϕ = ⎜⎜ v
⎝ M vs
⎞
⎟⎟ ⎠ V ,T
(5) Dall’equazione di stato si deduce anche: pv V
RT p V
= 18 vs
RT
M v = 18
M v ,s
da cui si ottiene ϕ=
pv
p vs
Elementi di psicrometria - 3/13
(6) Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
L’umidità relativa viene normalmente espressa in percentuale; il suo campo di variabilità è compreso fra 0 e 100%. Inoltre il titolo può essere messo in relazione con l’umidità relativa. Dalla definizione dell’umidità relativa si ricava infatti: pv = ϕ pvs mentre dalla definizione del titolo, si ha: x = 0 ,622
pv
pa
Sostituendo si ottiene allora: x = 0 ,622
ϕ p vs
pa
Esprimendo infine la pressione parziale dell’aria dalla relazione: pa = p − pv = p − ϕ pvs si ha: x = 0 ,622
ϕ pvs
p − ϕ p vs
(7) 1.1.3 Grado di saturazione
Il grado di saturazione è definito come il rapporto fra il titolo della miscela di volume V alla temperatura T ed il titolo in condizioni di saturazione alla stessa temperatura: ⎛ x
ψ = ⎜⎜
⎝ xS
⎞
⎟⎟ ⎠ V ,T
(8) Il grado di saturazione viene espresso in percentuale; il suo campo di variabilità è compreso fra 0 e 100%. E’ possibile mettere in relazione il grado di saturazione con l’umidità relativa. Infatti si ha: x = 0 ,622
pv
p − pv
x S = 0 ,622
p vs
p − p vs
e quindi ψ=
pv
p − pvs
x
=
⋅
x S p − pv
pvs
Ma poiché: ϕ=
pv
pvs
si ottiene: ψ = ϕ⋅
p − pvs
p − ϕ pvs
Elementi di psicrometria - 4/13
(9) Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
1.1.4 Temperatura di rugiada
Oltre alle grandezze in precedenza definite, per lo studio dell’aria umida vengono utilizzate alcune particolari temperature la cui conoscenza consente di determinare il contenuto di vapore d’acqua della miscela. Si definisce allora temperatura di rugiada la temperatura che, a parità di titolo e di pressione, dovrebbe avere l’aria per trovarsi in condizioni di saturazione. Partendo dalla relazione che definisce il titolo in condizioni di saturazione: x S = 0 ,622
p vs
p − p vs
ed essendo la trasformazione a titolo costante e quindi con xS = x, è possibile ricavare la pressione di saturazione: p vs =
px
0 ,622 + x
(10) e da essa la temperatura di saturazione, data la corrispondenza biunivoca che esiste tra pressione di saturazione e temperatura. 1.1.5 Temperatura di saturazione adiabatica
La temperatura di saturazione adiabatica è definita come la temperatura raggiunta da una miscela di aria umida quando, con un processo adiabatico, essa viene portata in condizioni di saturazione. La temperatura di saturazione adiabatica può essere valutata misurando la temperatura di bulbo umido; quest’ultima è pari alla temperatura misurata da un termometro il cui bulbo, avvolto in una garza imbevuta d’acqua, viene esposto ad un flusso d’aria. 1.2 Grandezze specifiche
In termodinamica le grandezze specifiche vengono riferite alla massa complessiva della miscela. In psicrometria invece esse vengono riferite alla sola massa di aria secca, che ha la proprietà di mantenersi invariata; si tratta pertanto di grandezze specifiche anomale, essendo riferite all’unità di massa di uno dei due componenti anziché a quella della miscela. La relazione generale che esprime la grandezza G in funzione dei valori assunti per l’aria secca e per il vapore d’acqua si ottiene utilizzando le regole valide per le miscele di gas perfetti: G = M a ga + M v gv (11) Riferendo il tutto all’unità di massa di aria secca, si ottiene allora: g=
M
M
G
= a ga + v gv Ma Ma
Ma
e quindi: g = ga + x gv (12) Consideriamo l’entalpia: per l’ipotesi che l’aria umida sia costituita da una miscela di gas ideali, è possibile esprimere l’entalpia della miscela come somma delle entalpie parziali dei componenti per cui, indicando con ha l’entalpia dell’aria secca e con hv quella del vapore d’acqua si ha: h = ha + x hv Elementi di psicrometria - 5/13
(13) Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
Sia l’entalpia dell’aria secca che quella del vapore d’acqua sono esprimibili in funzione della temperatura: ha = c pa Δt + ha 0
hv = c pv Δt + hv 0
(14) in cui cpa e cpv sono rispettivamente il calore specifico a pressione costante dell’aria secca e del vapore d’acqua ed ha0 e hv0 rappresentano i valori dell’entalpia per uno stato di riferimento. Per convenzione si assegna il valore 0 all’entalpia dell’aria secca a 0°C (la pressione non interessa essendo un gas perfetto) ed all’entalpia del vapore per liquido saturo a 0°C. Risulta allora: ha = c pa t
hv = c pv t + r
(15) in cui r il calore latente di vaporizzazione dell’acqua alla temperatura di 0°C, quest’ultimo necessario a vaporizzare a 0°C l’unita di massa di acqua. Sostituendo nella relazione (13) si ha: h = c pa t + x (c pv t + r ) (16) Da tale espressione si può ricavare il calore specifico a pressione costante della miscela: ⎛ ∂h ⎞
cp = ⎜
⎟ = c pa + x c pv ⎝ ∂T ⎠ p
(17) Poiché nelle normali condizioni di temperatura e pressione dell’aria si può assumere: c pa = 1,006
kJ
kJ
kJ
kJ
; c pv = 1,83
; r = 2501 . ≅1
kgK
kgK
kgK
kg
si ottiene infine: h = t + x (1,83t + 2501)
kJ
kg a
(18) 1.3 Diagrammi di Mollier e Psicrometrico
Lo stato fisico della miscela è definito, come visto, da tre parametri. Poiché, fra essi, la pressione è quasi sempre quella atmosferica, è sufficiente una rappresentazione bidimensionale per descrivere lo stato della miscela. A tal fine i più comuni diagrammi utilizzati sono quello di Mollier e quello psicrometrico. Il primo, tracciato in coordinate oblique, porta in ascissa il titolo ed in ordinata l’entalpia della miscela. Il secondo riporta in ascissa i valori della temperatura, ed in ordinata quelli del titolo; le entalpie si leggono su di una retta trasversale situata al di sopra della curva di saturazione. Una rappresentazione del diagramma psicrometrico è riportata in Figura 1. Elementi di psicrometria - 6/13
Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
Figura 1. Diagramma psicrometrico a pressione atmosferica. Dato quindi un certo stato termodinamico dell’aria, definito mediante due delle variabili di stato, i diagrammi consentono in modo agevole di determinare le altre. In essi sono infatti chiaramente individuabili le isoterme, le isoentalpiche, le isocore, le isotitolo e le curve a grado igrometrico costante; in particolare la curva ϕ = 100% è detta curva di saturazione. 1.4 Trasformazioni termodinamiche
Si consideri di sottoporre una certa portata d’aria umida G& a che si trova nelle condizioni iniziali h1, x1, T1 ad una trasformazione che la porti nelle condizioni finali h2, x2, T2. Durante questa trasformazione, dal primo principio della termodinamica è possibile ricavare la quantità di calore scambiata nell’unità di tempo: Q& = G& a (h2 − h1 ) . Sostituendo l’espressione dell’entalpia si ha: Q& = G& a [c pa t 2 + x 2 (c pv t 2 + r ) − c pa t 1 + x 1 (c pv t 1 + r )] Q& = G& a (c pa + c pv x 2 ) t 2 − (c pa + c pv x 1 ) t 1 + r x 2 − r x 1 Q& = G& a [c p (t 2 − t 1 ) + r (x 2 − x 1 )] [
]
(19) avendo supposto per il calore specifico dell’aria umida un valore costante tra le due temperature t1 e t2. Si ha allora che lo scambio complessivo può essere espresso come somma di due aliquote, una dovuta alla variazione di temperatura ed una dovuta al cambiamento di fase dell’acqua. Il primo di questi scambi, Q& S , è detto scambio sensibile: Q& S = G& a c p (t 2 − t 1 ) (20) mentre il secondo, Q& L , è detto scambio latente: Q& L = G& a r (x 2 − x 1 ) Elementi di psicrometria - 7/13
(21) Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
Sul diagramma psicrometrico la trasformazione viene individuata da un segmento, avente una certa pendenza, che congiunge i punti iniziale e finale della trasformazione stessa. È possibile valutare la pendenza della trasformazione nel piano t‐x mediante il rapporto: R=
Q& S
Q&
(22) fra il scambio sensibile e quello complessivo. Il termine R, detto fattore termico, è determinabile sul diagramma psicrometrico per mezzo di un’apposita scala. 1.4.1 Miscelazione di due portate
Nel momento in cui due portate d’aria che si trovino in differenti condizioni vengono tra loro miscelate, lo stato termodinamico a cui si porterà la miscela può essere ricavato applicando l’equazione di continuità ed il primo principio della termodinamica. Siano G&1 , h1 , x 1 ,t 1 e G& 2 , h2 , x 2 , t 2 le condizioni iniziali delle due portate d’aria e G& 3 , h3 , x 3 , t 3 quelle risultanti dalla loro miscelazione. G& 1 , h1 , x 1 ,t 1
G& 3 , h3 , x 3 , t 3
G& 2 , h2 , x 2 , t 2
Figura 2. Miscelazione di due portate. Applicando l’equazione di continuità alla portata d’aria si ha: G& a1 + G& a 2 = G& a3 (23) e per la portata di vapore: G& v1 + G& v 2 = G& v 3 G& a1 x1 + G& a 2 x 2 = G& a3 x 3 (24) Dal primo principio della termodinamica si ha N
Q& = ∑ G& i hi (25) i =1
e, supponendo che la miscelazione avvenga adiabaticamente: G& a1 h1 + G& a 2 h2 = G& a3 h3 Sostituendo la (23) nella (26) Elementi di psicrometria - 8/13
(26) Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
(
)
G& a1 h1 + G& a 2 h2 = G& a1 + G& a 2 h3 da cui si ricava: h3 =
G& a1h1 + G& a 2 h2
G& a3
Si ha inoltre che: G& a1 (h1 − h3 ) = G& a 2 (h3 − h2 ) e quindi: G& a1 h3 − h2
=
G& a 2 h1 − h3
h2
(27) h
h3
x
ϕ = 100%
h1
3
2
1
t
Figura 3. Rappresentazione sul diagramma psicrometrico della miscelazione tra due portate. Riportando le grandezze sul diagramma psicrometricco si ha: G& a1 h3 − h2 32
=
= G& a 2 h1 − h3 13
che consente di determinare geometricamente le coordinate del punto 3. 1.4.2 Riscaldamento o raffreddamento sensibile
Una trasformazione di riscaldamento o di raffreddamento sensibile avviene facendo variare la temperatura mantenendo costante il titolo. Sul diagramma psicrometrico tale trasformazione è descritta da una retta avente pendenza R=±1. Elementi di psicrometria - 9/13
Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
h
ϕ = 100%
x
2
3
1
4
t
Figura 4. Rappresentazione sul diagramma psicrometrico di trasformazioni di riscaldamento e di raffreddamento sensibile. Il riscaldamento sensibile della miscela può essere illimitato, mentre il raffreddamento può procedere fino alla temperatura di rugiada: al di sotto di tale temperatura avviene infatti la condensazione del vapore ed il titolo diminuisce. La potenza termica che viene scambiata nel raffreddamento o nel riscaldamento sensibile di una massa d’aria Ga è data dalla relazione: Q& S = G& a c p (t 2 − t 1 ) 1.4.3 Raffreddamento e deumidificazione
Se si abbassa la temperatura al di sotto della temperatura di rugiada si ha la condensazione del vapore ed una diminuzione del titolo che si mantiene pari al titolo in condizioni di saturazione alla temperatura della miscela. La potenza termica che viene scambiata nel raffreddamento e deumidificazione di una massa d’aria Ga è data dalla relazione: Q& = G& a [c p (t 2 − t1 ) + r (x 2 − x1 )] Elementi di psicrometria - 10/13
Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
h
ϕ = 100%
x
1
2
t
Figura 5. Rappresentazione sul diagramma psicrometrico di una trasformazione di raffreddamento e deumidificazione. Spesso per ottenere questa trasformazione l’aria viene messa in contatto in scambiatori di calore con serpentine che si trovano a temperatura superficiale inferiore a quella di rugiada della miscela di partenza. Attorno ai tubi si crea uno strato d’aria satura che miscelandosi con l’aria in condizioni iniziali forma una miscela che, in un tempo infinito, tende ad assumere le condizioni che si hanno sulla superficie dei tubi. La trasformazione viene comunque arrestata in un punto prossimo alle condizioni di saturazione; in questo caso il rapporto 1F/12 è detto fattore di bypass. h
ϕ = 100%
x
1
2
F
t
Figura 6. Rappresentazione sul diagramma psicrometrico di una trasformazione di raffreddamento e deumidificazione mediante l’uso di scambiatori di calore. 1.4.4 Umidificazione
L’umidificazione avviene fornendo all’aria una quantità d’acqua che può essere allo stato di vapore o di liquido. Il contenuto d’acqua da aggiungere sarà pari a: Elementi di psicrometria - 11/13
Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
G& L = G& v 2 − G& v1 = G& a (x 2 − x1 ) (28) L’entalpia alla fine dalla trasformazione sarà: h2 = h1 + (x 2 − x 1 )hv (29) Se l’acqua viene aggiunta allo stato di vapore l’entalpia del vapore sarà pari a quella del vapore surriscaldato alla temperatura e pressione corrispondenti. Se viene aggiunta sotto forma di liquido si avrà: hv = c pv t + r (30) G& a1 = G& a 2 = G& a
G& a1 x1 + G& L = G& a 2 x 2 = G& a x 2 G& a1h1 + G& L hv = G& a 2 h2 = G& a h2
(31) In questo caso si avrà: Poiché G& L<< +G& a si ha: G& a1h1 + G& L hv ≅ G& a1h1 e quindi: G& a1h1 = G& a h2 ⇒ h1 = h2 Il processo è quindi isentalpico e la trasformazione è detta di saturazione adiabatica. Essa avviene in organi detti saturatori adiabatici in cui l’acqua finemente polverizzata viene investita da un flusso d’aria e passa quindi nella miscela; l’acqua in eccesso viene recuperata in una vaschetta. Figura 7. Rappresentazione schematica di un saturatore adiabatico. Elementi di psicrometria - 12/13
Prof. Ing. Antonino Nucara - Appunti del Corso di Tecnica del Controllo Ambientale - a.a. 2009/10
h
ϕ = 100%
x
2
1
t
Figura 8. Rappresentazione sul diagramma psicrometrico di una trasformazione di saturazione adiabatica. Elementi di psicrometria - 13/13