Relazione di laboratorio di telecomunicazioni.
23/01/2014
Titolo: Carica di un condensatore.
Obiettivi:
Calcolare Tau con la formula R x C.
Calcolare la Vc per ogni istante t (da t = 0 ms a t = 1 ms).
Realizzare la tabella e il grafico.
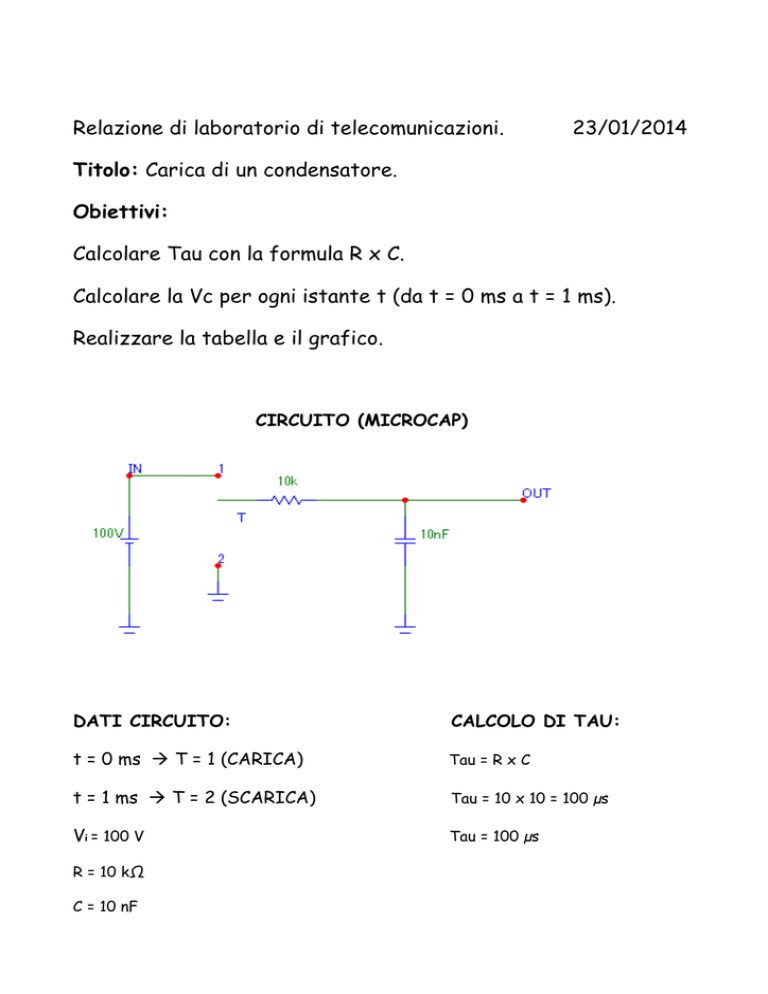
CIRCUITO (MICROCAP)
DATI CIRCUITO:
CALCOLO DI TAU:
t = 0 ms T = 1 (CARICA)
Tau = R x C
t = 1 ms T = 2 (SCARICA)
Tau = 10 x 10 = 100 µs
Vi = 100 V
Tau = 100 µs
R = 10 kΩ
C = 10 nF
Condizioni iniziali: l’interruttore T è aperto, il condensatore è
inizialmente scarico e la differenza di potenziale sul condensatore è 0 V.
Chiudendo l’interruttore T 1 all’istante t = 0 ms le cariche si
accumulano sulle due armature in seguito all'applicazione di
una differenza di potenziale. Il condensatore comincia a caricarsi ed è
carico dopo circa 5 Tau, come dimostrano tabella e grafico.
Mettendo T 2 il condensatore, completamente carico, comincia a
scaricarsi.
TABELLA
Tau
0τ
1τ
2τ
3τ
4τ
5τ
6τ
7τ
8τ
9τ
10τ
t(ms)
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
Vc(V)
0
63,21
86,47
95,02
98,17
99,33
99,75
99,91
99,97
99,99
100
Nota: all’istante t = 0 la tensione sul condensatore è uguale a 0 V.
Tensione all’istante t:
Vc(t) = E * [1 – (e ^ -t/Tau)]
2
GRAFICO
Asse verticale: Tensioni [V]
Asse orizzontale: Tempi [ms]
Grafico del potenziale (V) in funzione del tempo (t).
Nota: all’istante t = 0 la tensione sul condensatore è uguale a 0 V.
Nota: l’andamento è esponenziale crescente.
3
Giacomo Colantonio Giorgio Grosso
Classe 4T 23/01/2014
Misura 3: Scarica di un condensatore
Circuito (micro-cap)
Elenco componenti
Dati
Vi = 100V
t = 1m T2(Scarica)
R = 10KΩ
TAU=R*C = 10*10 =1OOuS
C = 10nF
Vco = 0
Tabella Dati
0
1τ
2τ
3τ
4τ
5τ
6τ
7τ
8τ
9τ
10τ
t(ms)
=
0
= 0,1
= 0,2
= 0,3
= 0,4
= 0,5
= 0,6
= 0,7
= 0,8
= 0,9
= 1
Vc(V)
100,00
36,79
13,53
4,98
1,83
0,67
0,25
0,09
0,03
0,01
0,00
4
Grafico
Il generatore parte da 100 V e con il passare del tempo si scarica.
Il grafico mostra come la corrente aumenti con il diminuire della tensione.
5
RELAZIONE DI TELECOMUNICAZIONE
CIRCUITO 2A
Circuito RC, carica e scarica di un condensatore.
Circuito alimentato da un generatore d’onda quadra con :
(frequenza) f = 1KHz e
(Ampiezza) A = 10V -> Viniziale = 0v ; Vfinale = 10v.
R1=10kΩ
C1=10 nF
V1= generatore onda quadra
Simulazione Onda:
6
Quindi l’equazione alla maglia sarà : V1 = Vc1(t) +Vr1
La corrente I(t) nel circuito risulta essere variabile nel tempo a causa del cambio di tensione a capo dei
terminali del condensatore.
I(t) = E/R * e-t/RC
ANALISI DEL COMPORTAMENTO AL VARIARE DELL’ALIMENTAZIONE
Tau= R1 * C1 = 10k * 10nf = 100 microsecondi (è un valore costante detta costante di tempo del circuito.
Ovvero un valore che serve a considerare il condensatore carico dal punto di vista operativo.)
Per tanto possiamo affermare che il periodo in cui si carica è di 500 micro secondi ovvero 0.5 milli secondi
che è lo stesso tempo che ci mette a scaricarsi, ovvero 5 Tau
La carica e la scarica del condensatore avvengono in maniera esponenziale.
7
Enrico Sella Nora , Michele Spinelli
4°Ttlc
6/01/14
Misura 3: Carica e Scarica di un condensatore (2B)
Dati:
R1 = 10kΩ
C = 10nF
V1 =10Volt
τ=?
VR = ?
Schema elettrico:
8
Calcoli teorici:
τ = R1 * C = 10kΩ * 10nF = 100μs
VR = Vin-Vc
Spiegazione:
Al tempo t=0 la capacità è scarica e nel circuito il valore della corrente è limitato dalla sola resistenza R ed è
pari a I = Vin / R = 1mA. Quindi il valore della tensione ai capi della resistenza è inizialmente uguale al valore
massimo dell’onda quadra in ingresso (VR = Vin = 10V).
Negli istanti di tempo successivi la tensione ai capi del condensatore aumenta mentre quella ai capi della
resistenza diminuisce; questo causa un decremento della corrente nel circuito.
La corrente assume un valore pari a I = (Vin –VC) /R perciò diventa nulla (I = 0mA) dopo un tempo pari a τ,
cioè quando la tensione ai capi del condensatore raggiunge il valore massimo dell’onda quadra (VC = Vin =
10V).
Ora il condensatore è carico con una tensione pari a quella della batteria (Vin); la corrente però circola nel
verso opposto, quindi la tensione ai capi della resistenza invertirà la polarità diventando uguale a -VR = -Vin
= -10V.
La capacità ora si scaricherà seguendo la stessa legge della carica per un tempo τ, dopo di che si
ripresenterà la situazione iniziale e così via.
9
Grafico:
Scarica Vc iniziale = 10V
Carica Vc iniziale = -10V
Vc finale = 0V
I valori sull’asse delle ascisse rappresentano il tempo in ms.
I valori sull’asse delle ordinate rappresentano la tensione VR in Volt.
10
RELAZIONE DI TLC
CIURCUITO 3A
Elenco componenti:
• Resistenza da 10 kΩ
• Condensatore da 1 nF
• Generatore di onde quadre
Formule teoriche:
Vc(iniziale)= 0V
Vc(finale)= 10V
= R * C = 10k * 1n = 10 µS
Carica completa in 5 (circa)
Considerazioni: La carica e la scarica del condensatore avviengono in maniera esponenziale. A
differanza del circuito 2A, in quanto il condesatore è più piccolo, la carica e la scarica avvengono in
un tempo minore.
11
3b)
Schema Elettrico
Elenco Componenti:
-R1 = 10KΩ
-C1 = 100nF
-V1 = Generatore ad onde quadre
Forma d'onda:
Della forma d'onda in questione sono stati presi gli ultimi due periodi di dieci, poiché i valori
minimi e massimi di carica e scarica hanno bisogno di tempo per stabilizzarsi.
Formule Teoriche:
- = R * C = 10KΩ * 100nF = 1000µs = 1ms
12
Carica
Scarica
VC Iniziale
3,7V
6,2V
VC Finale
6,2V
3,7V
I valori sono uno l'opposto dell'altro dato che dove finisce la carica inizia la scarica.
In questo circuito il condensatore non raggiunge mai la carica completa.
Considerazioni:
Come dimostrato in figura con questo circuito il Condensatore non raggiunge la carica massima a
differenza degli altri circuiti, ciò è dovuto alle sue dimensioni (100nF) troppo elevate per poterlo
caricare completamente in un lasso di tempo così piccolo, quindi il condensatore si troverà a
caricarsi e a scaricarsi intorno ad un valore che oscilla dai 3.5V minimi e i 6,5V massimi.
13
Cafaro Marco
IV T Tlc
22/01/14
Misura 3: carica e scarica condensatore (4a)
Schema elettrico:
Dati:
Vin= 10V
R1=10kΩ
R2=10kΩ
C=10nF
Calcoli teorici:
carica: Req=R1*R2/(R1+R2)=5KΩ
14
ĩ = Req * C = 5 * 10 = 50µS
scarica: Req=R1*R2/(R1+R2)=5KΩ
ĩ = Req * C = 5 * 10 = 50µS
CARICA:
VC iniziale
0V
- VC finale
5V
-
Tau
50 µS
SCARICA:
VC iniziale
5V
- VC finale
0V
-
Tau
50 µS
Grafico:
15
Osservazioni:
Utilizzando il teorema di Thevenin e cortocircuitando gli altri dispositivi oltre alle resistenze,
possiamo ricavare la resistenza equivalente (Req) che corrisponde al parallelo tra le due resistenze
R1 ed R2 le quali avendo lo stesso valore forniranno una resistenza equivalente che vale la metà.
Conoscendo la resistenza equivalente possiamo successivamente calcolare il valore di TAU con la
formula:
ĩ = Req * C
La resistenza equivalente (Req) di carica sarà uguale a quella di scarica e di conseguenza anche i
valori della TAU di carica e della scarica saranno uguali.
Possiamo notare dal grafico che la tensione assorbita dal condensatore è la metà di quella che
fornisce il generatore perché il condensatore essendo collegato in parallelo alla resistenza R2
potrà caricarsi al massimo fino al raggiungimento della tensione presente ai capi di R2.
Essendo R1 in serie con R2 ed avendo lo stesso valore di resistenza, la tensione verrà suddivisa a
metà tra ciascuna resistenza Vc = VR2 = Vin / (R1 + R2) * R2
16
Cardo Davide
IV T Tlc
22/01/14
Misura 3: carica e scarica condensatore (4b)
Schema elettrico:
Dati:
Vin = 10V
R1=10kΩ
R2=10kΩ
C=10nF
Calcoli teorici:
carica: Req=R1*R2/(R1+R2)=5KΩ
ĩ = Req * C = 5 * 10 = 50µS
scarica: Req=R2=10kΩ
ĩ = R2 * C = 10 * 10 = 100µS
CARICA:
VC iniziale
0V
- VC finale
5V
-
Tau
50 µS
SCARICA:
VC iniziale
5V
- VC finale
0V
-
Tau
100 µS
17
Grafico:
Osservazioni:
Nella fase di carica il diodo sarà polarizzato direttamente quindi possiamo calcolare la resistenza
equivalente (Req) facendo il parallelo tra le resistenze R1 e R2.
Calcoliamo il TAU moltiplicando la resistenza equivalente (Req) per la capacità del condensatore.
Nella fase di scarica invece, il diodo viene polarizzato inversamente quindi la resistenza
equivalente (Req) sarà soltanto la R2 perchè il diodo si comporta come un circuito aperto e quindi
la corrente non passerà sulla resistenza R1.
Calcoliamo quindi la TAU di scarica moltiplicando quindi la resistenza equivalente (Req) che sarà
R2 per la capacità del condensatore.
18
Noteremo che la TAU di scarica sarà il doppio di quella di carica questo perché cambiano i valori
delle resistenze equivalenti dove nella carica avremo il parallelo tra la R1 e la R2 mentre nella
scarica avremo solamente la R2.
Possiamo notare dal grafico che la tensione assorbita dal condensatore è la metà di quella che
fornisce il generatore perché il condensatore essendo collegato in parallelo alla resistenza R2
potrà caricarsi al massimo fino al raggiungimento della tensione presente ai capi di R2.
Essendo R1 in serie con R2 ed avendo lo stesso valore di resistenza, la tensione verrà suddivisa a
metà tra ciascuna resistenza Vc = VR2 = Vin / (R1 + R2) * R2
.
19












