Strumenti

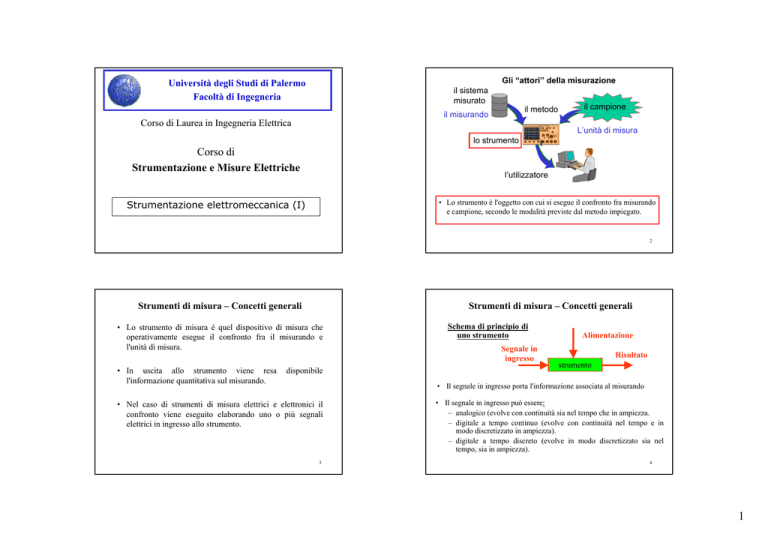
Gli “attori” della misurazione
Università degli Studi di Palermo
Facoltà di Ingegneria
il sistema
misurato
il metodo
il misurando
Corso di Laurea in Ingegneria Elettrica
il campione
L’unità di misura
lo strumento
Corso di
Strumentazione e Misure Elettriche
l’utilizzatore
• Lo strumento è l'oggetto con cui si esegue il confronto fra misurando
e campione, secondo le modalità previste dal metodo impiegato.
Strumentazione elettromeccanica (I)
2
Strumenti di misura – Concetti generali
Strumenti di misura – Concetti generali
• Lo strumento di misura è quel dispositivo di misura che
operativamente esegue il confronto fra il misurando e
l'unità di misura.
• In uscita allo strumento viene resa
l'informazione quantitativa sul misurando.
disponibile
Schema di principio di
uno strumento
Segnale in
ingresso
Alimentazione
Risultato
strumento
• Il segnale in ingresso porta l'informazione associata al misurando
• Nel caso di strumenti di misura elettrici e elettronici il
confronto viene eseguito elaborando uno o più segnali
elettrici in ingresso allo strumento.
3
• Il segnale in ingresso può essere:
– analogico (evolve con continuità sia nel tempo che in ampiezza.
– digitale a tempo continuo (evolve con continuità nel tempo e in
modo discretizzato in ampiezza).
– digitale a tempo discreto (evolve in modo discretizzato sia nel
tempo, sia in ampiezza).
4
1
Strumenti di misura – Concetti generali
Schema di principio di
uno strumento
Segnale in
ingresso
Strumenti di misura – Concetti generali
Schema di principio di
uno strumento
Alimentazione
Segnale in
ingresso
Risultato
strumento
Alimentazione
Risultato
strumento
• Il risultato della misura fornisce l'informazione quantitativa sul
misurando
• Lo strumento elabora il segnale in ingresso e fornisce il risultato
• L’alimentazione preleva l’energia necessaria al funzionamento dello
strumento da una sorgente esterna; essa può essere:
– indipendente dal circuito di misura (strumenti elettronici)
– lo stesso segnale in ingresso (strumenti elettromeccanici)
• Il risultato della misura può essere espresso in forma:
– analogica (deviazione di un indice su una scala graduata).
– numerica (visualizzazione su un display numerico)
5
6
7
8
2
Caratteristiche di uno strumento di misura
Caratteristiche di uno strumento di misura
•
•
•
•
•
•
• Portata: indica il campo di valori ammessi per il misurando, per i
quali lo strumento è adatto. Il valore massimo ammissibile per il
misurando (limite superiore della portata) viene anche indicato
come valore di fondo scala (o fondo scala) dello strumento.
• Generalmente i numeri letti sulla scala dello strumento non
indicano direttamente il valore della grandezza misurata. La lettura
è spesso effettuata in numero di divisioni.
• Per ottenere il valore della grandezza misurata, occorre
moltiplicare la lettura (numero di divisioni) per la costante
strumentale (rapporto tra la portata e la corrispondente
indicazione sulla scala).
• Esistono strumenti a più portate, a ciascuna delle quali
corrisponde una diversa costante strumentale
Portata
Limiti di impiego
Precisione, Accuratezza
Sensibilità
Risoluzione
Consumo
9
10
Caratteristiche di uno strumento di misura
Caratteristiche di uno strumento di misura
• Limiti di impiego: il campo di valori delle grandezze di influenza
entro cui lo strumento conserva le sue caratteristiche. Tra essi vi sono:
– Forma d’onda del segnale in ingresso,
– Larghezza di banda del segnale in ingresso (il campo di frequenza
entro il quale possono cadere le componenti spettrali del segnale in
ingresso senza che le prestazioni metrologiche dello strumento
siano compromesse),
– Temperatura (sia ambientale che dovuta al riscaldamento proprio
dello strumento)
– Campi elettrici e magnetici prodotti da fattori esterni
– Posizione di impiego dello strumento (orizzontale, verticale
inclinata)
– Valore delle tensioni ausiliarie di alimentazione, (per gli strumenti
elettronici)
– Valori massimi di tensione e corrente
11
• Accuratezza: Grado di concordanza tra il risultato di una misurazione
ed un valore vero del misurando. Viene espressa in modo diverso a
seconda se si considerano strumenti elettromeccanici o digitali.
• Precisione: capacità di uno strumento di fornire risultati di misura poco
discosti fra di loro.
• Classe: in genere viene fornito il valore massimo di accuratezza per
uno strumento (massimo scostamento tra valore misurato e valore
atteso). Sulla base di questo valore viene definita la classe dello
strumento. La classe rappresenta l’ampiezza della fascia di incertezza,
espressa in percento del fondo scala, valida per ogni punto della scala
stessa, in condizioni prefissate
– Es: uno strumento in classe 0,5 è uno strumento la cui accuratezza
definisce un intervallo del ±0,5% attorno al valore atteso
12
3
Strumenti elettromeccanici
Classe di precisione
L’indice di classe coincide con l’ampiezza in valore relativo
della fascia di valori del misurando quando la grandezza
misurata è pari alla portata. Per valori più piccoli tale
ampiezza (in valore relativo) aumenta
• Si definisce come:
Cl = 100
Emax
Indicando con a la semiampiezza dei possibili valori del misurando
P
• dove Emax errore assoluto massimo (in tutto il campo di
misura) e P portata quindi rappresenta l’errore assoluto in
% del fondo scala. Coincide con l’errore relativo quando la
grandezza misurata è pari alla portata. Per valori più piccoli
l’errore relativo aumenta.
• Valori tipici:
– 0,05 ÷ 0,1 strumenti campione da laboratorio
– 0,2 ÷ 0,5 strumenti da laboratorio
– 1; 1,5; 2,5; 5 strumenti industriali e da quadro
Emax
ClP
Emax =
P
100
E
ClP
a% = 100 max =
M
M
Se M = P a% = Cl
Cl = 100
Se M =
P
a% = 2Cl
2
13
14
Consumo di uno strumento di misura
Caratteristiche di uno strumento di misura
• Sensibilità: capacità di uno strumento di indicare variazioni del
misurando; è definita come rapporto fra una variazione Δx della
grandezza misurata e la corrispondente variazione Δδ della
deviazione dello strumento (Strumentazione elettromeccanica).
Spesso coincide con la risoluzione che si ha in corrispondenza
del fondo scala minimo (Strumentazione digitale).
• Risoluzione: Per uno strumento analogico rappresenta la più
piccola variazione della grandezza da misurare che lo strumento
può indicare con sicurezza in una determinata portata. Per uno
strumento digitale è data dal valore della cifra minima
visualizzabile nella portata selezionata.
15
• Ogni strumento di misura modifica il sistema in cui è inserito, creando
una perturbazione nella stessa grandezza da misurare. Gli strumenti
elettrici presentano una o più coppie di morsetti per il collegamento
con i circuiti esterni, dai quali assorbono potenza attiva e reattiva (in
corrente alternata).
• La potenza assorbita può alterare le condizioni del circuito in cui lo
strumento è inserito, dando luogo ad un errore di consumo (o, a volte,
a delle limitazioni di impiego degli strumenti stessi).
• Questo effetto è esprimibile attraverso l’impedenza che lo strumento
presenta ai suoi morsetti di ingresso, che deve essere tale da ridurre al
minimo il consumo dello strumento stesso.
• Nel caso in cui, invece, lo strumento disponga di circuiti ausiliari,
alimentati da sorgenti esterne, l’assorbimento di potenza non altera il
misurando; la potenza dissipata nello strumento determina comunque
un riscaldamento interno, che può richiedere un certo tempo per
raggiungere la condizione di regime, rispetto alla quale sono definite
le caratteristiche metrologiche dello strumento stesso.
16
4
Classificazione degli strumenti in base al
misurando
Classificazione degli strumenti in base al
misurando
• Strumenti a un ingresso:
– Misuratori di tensione: voltmetri
• analogici, digitali, per tensioni continue, per tensioni alternate
(di picco, a valor medio, a vero valore efficace)
• Analizzatori di forma d'onda: Oscilloscopi (nel dominio del
tempo), Analizzatori spettrali (nel dominio della frequenza)
– Misuratori di corrente: amperometri
• Analogici, digitali, per correnti continue, per correnti alternate
(Amperometri di picco, a valor medio, a vero valore efficace
• Galvanometri (indicatori di zero)
– Misuratori di tempo e frequenza (frequenzimetri, counter)
– Strumenti integratori
• Misuratori di carica
• Strumenti a due ingressi:
– Moltiplicatori
– Misuratori di potenza: wattmetri
• Wattmetri analogici, digitali, per regimi stazionari (cc), per
regimi alternati (ca)
– Misuratori di potenza reattiva (varmetri)
– Misuratori di energia (strumenti integratori - contatori)
– Logometri (strumenti che eseguono un rapporto)
• Ohmetri (misuratori di resistenza)
– Impedenzimetri (misuratori di impedenza)
• Esistono sia strumenti analogici, sia strumenti digitali
17
Voltmetri - generalità
Voltmetri - generalità
• Il voltmetro è uno strumento a due morsetti che misura la
tensione in una sezione di un circuito elettrico.
• I morsetti devono essere collegati ai terminali della sezione di
circuito su cui si vuole misurare la tensione.
• Il voltmetro deve essere inserito in parallelo all'elemento
circuitale ai cui morsetti si vuole misurare la tensione.
I
V
V
18
• Il voltmetro ideale non deve perturbare
il circuito su cui vengono eseguite le
misure di tensione. Questo significa
che non deve assorbire corrente dal
circuito cui è collegato (I = 0).
• L'impedenza interna del voltmetro
deve essere: Zv = ∞.
19
• Un voltmetro reale ha impedenza interna elevata, ma non infinita.
L'ordine di grandezza va dai 104 Ω (voltmetri elettromeccanici,
impedenza induttiva) ai 106 Ω (voltmetri elettronici, impedenza
capacitiva).
• Per questo motivo i voltmetri reali sono percorsi da una corrente. La
presenza di questa corrente costituisce un contributo sistematico
all'incertezza di misura.
• E' necessario tenerne conto, apportando le necessarie correzioni al
risultato della misura. (La natura delle correzioni da apportare
dipende dal tipo di misura effettuata).
20
5
Amperometri - generalità
Amperometri - generalità
• L'amperometro è uno strumento a due morsetti che misura la
corrente circolante in un lato di un circuito elettrico.
• I morsetti devono essere collegati in modo tale che
l'amperometro sia percorso dalla corrente che si intende
misurare.
• L'amperometro deve quindi essere inserito in serie al lato del
circuito di cui si vuole misurare la corrente.
• L'amperometro ideale non deve perturbare il circuito su cui viene
eseguita le misure di corrente. Ciò significa che non deve causare
cadute di tensione sul lato a cui è collegato (ΔV = 0).
• Gli amperometri reali hanno impedenza interna piccola, ma non
nulla. L'ordine di grandezza è di qualche ohm. Per questo
motivo sugli amperometri reali si localizza una caduta di
tensione.
• La presenza di questa caduta di tensione costituisce un
contributo sistematico all'incertezza di misura.
• E' necessario tenerne conto, apportando le necessarie correzioni
al risultato della misura. (La natura delle correzioni da apportare
dipende dal tipo di misura effettuata).
I
• L'impedenza interna
dell’amperometro deve
essere: Za = 0.
A
ΔV
21
22
Wattmetri - generalità
Wattmetri - generalità
• I wattmetri sono strumenti a quattro morsetti che misurano la
potenza elettrica in una sezione di un circuito.
• Poiché la potenza elettrica dipende dalla corrente che transita
nella sezione e dalla tensione sulla sezione, i wattmetri
dovranno avere un ingresso in corrente e un ingresso in
tensione.
• I due morsetti di corrente si collegano in serie al circuito, e i due
morsetti di tensione si collegano in parallelo
• Il wattmetro ideale non deve perturbare il circuito su cui
vengono eseguite le misure di potenza. Questo significa che i
circuiti amperometrici non devono causare cadute di tensione
sul lato a cui sono collegati e i circuiti voltmetrici non devono
prelevare corrente dai morsetti a cui sono collegati.
• L'impedenza dei circuiti amperometrici deve essere Za = 0 e
l'impedenza dei circuiti voltmetrici deve essere Zv = ∞.
• Nei wattmetri reali l'impedenza dei circuiti amperometrici è
piccola, ma non nulla, e l'impedenza dei circuiti voltmetrici è
grande, ma non infinita. Per questo motivo i wattmetri
provocano sia cadute di tensione, sia assorbimenti di corrente.
Vengono così generati dei contributi sistematici all'incertezza di
misura
• E' necessario tenerne conto, apportando le necessarie correzioni
al risultato della misura.
W
P
23
24
6
Strumenti elettromeccanici
Strumenti elettromeccanici
• Sono basati sulla conversione della grandezza elettrica da
misurare in una forza, o, più spesso, in una coppia
• La grandezza da misurare viene trasformata in una coppia
applicata a un equipaggio di misura elettromeccanico a
indice, mediante un opportuno circuito. La potenza per il
funzionamento dello strumento viene prelevata dal circuito
di misura. L'indice si muove su una scala graduata
seguendo in modo analogo l'andamento della grandezza da
misurare, da cui si dicono anche analogici.
• I diversi tipi di strumenti elettromeccanici possono
distinguersi in base alla relazione che lega la coppia
motrice con la grandezza elettrica in ingresso (relazione di
tipo proporzionale, quadratico o più complessa)
Schema di uno strumento elettromeccanico:
• C (X) = azione motrice (funzione del misurando X)
• C (δ)= azione resistente (funzione della deviazione angolare)
• A regime, all’equilibrio
C (X) = C (δ)
• Quando si hanno due grandezze di ingresso, la coppia può
essere funzione del loro prodotto o del loro quoziente.
• Quando la grandezza di ingresso è variabile nel tempo
risulta variabile anche la coppia; la deviazione dell’indice
sulla scala dipende allora anche dalle caratteristiche
meccaniche dello strumento, ovvero dalla relazione tra
coppia motrice e posizione dell’equipaggio. Tale relazione
è legata alla funzione di trasferimento propria
dell’equipaggio mobile.
25
Strumento
elettromeccanico
27
26
Strumento elettromeccanico indicatore
28
7
Strumenti
elettromeccanici
Strumenti elettromeccanici
Cmotrice = Cresistente
Lo strumento ha una parte fissa ed un
equipaggio mobile. La grandezza da
misurare produce un’azione motrice
sull’ equipaggio mobile a cui si
oppone un azione resistente, funzione
della
deviazione,
normalmente
fornita da una molla. All’equilibrio le
due azioni sono uguali ed è quindi
possibile associare alla deviazione
dell’indice la grandezza da misurare.
29
Cmotrice = Cresistente ± Cattrito.
• Il valore della coppia d’attrito dipende in massima parte
del tipo di sospensioni dello strumento, oltre che dal peso
dell’equipaggio mobile, che deve essere il più leggero
possibile.
• Un indice di qualità dello strumento è il rapporto tra la
coppia motrice e la coppia d’attrito; poiché quest’ultima
dipende dal peso dell’equipaggio mobile, si può utilizzare
come indice di qualità il seguente rapporto:
Cm
con p = peso equipaggio mobile
30
p
Sospensioni
Caratteristiche generali degli strumenti
elettromeccanici
•
•
•
•
•
•
• In realtà esiste anche una coppia dovuta all’attrito, che
introduce nella condizione di equilibrio un termine
aggiuntivo che può essere positivo o negativo, ma sempre
di segno tale da opporsi al moto.
Le sospensioni hanno il compito di sostenere l’equipaggio mobile, riducendo
quanto più possibile le coppie di attrito, che si esplicano in corrispondenza
all’appoggio dell’equipaggio mobile sulla parte fissa dello strumento..
Negli strumenti più comuni, l’equipaggio mobile è montato su perni
cilindrici in alluminio, con punte in acciaio indurito levigate a sfera nella
parte terminale. I perni appoggiano su supporti in pietra dura, di forma
emisferica al fondo (R = 2÷3 r). Il raggio a della superficie d’appoggio è
dell’ordine di qualche micron.
Sospensioni
Molle
Scala graduata
Indici
Sistemi di smorzamento
Contrassegni
Sospensioni
a perni
31
r
R
Il dimensionamento risulta dal
compromesso fra l’esigenza di una
piccola coppia d’attrito (proporzionale ad
a) e quella di limitare le sollecitazioni dei
materiali costituenti il perno e il supporto
(proporzionali ad a2)
32
8
Sospensioni
Il buono stato delle sospensioni si controlla battendo leggermente sullo
strumento, per verificare che esso non modifichi la sua posizione di
equilibrio.
Oltre all’aumento della coppia d’attrito, il consumo del supporto provoca
una non corretta posizione dell’asse del perno, che da luogo ad un errore di
lettura (detto errore di traboccamento)
Sospensioni
a molle
Il pericolo di danneggiamenti dovuti ad
urti o a vibrazioni può essere ridotto
adottando supporti ammortizzati
mediante molle.
33
Per avere coppie di attrito ancora più
basse, si utilizzano le sospensioni a filo.
Esse si realizzano mediante un sottile
filo (quarzo o metallo) che sostiene la
parte mobile, fornendole la coppia
antagonista.
Questa sospensione consente coppie
ancora più piccole di quella a nastro ma
risulta più delicata ed ingombrante.
In genere questi strumenti hanno un
indice luminoso, per ridurre il peso
dell’equipaggio mobile.
Per assicurare la corretta posizione
della parte mobile, occorre che lo
strumento sia messo in una ben precisa
posizione, mediante bolla di livello.
L’equipaggio è molto sensibile agli urti
e deve essere meccanicamente bloccato
durante i trasporti (a volte si utilizza
una molla di richiamo che evita le
oscillazioni causate dagli urti).
Con le sospensioni a perni si realizzano
strumenti di classe fino a 0,5 (talvolta 0,2); non
si può andare oltre a causa dell’attrito.
Per strumenti di precisione si utilizzano le
sospensioni a nastri. Esse sono realizzate con
due nastri metallici (in platino-nichel o rameberillio, lunghi circa 10 mm), sottoposti tramite
molle ad uno sforzo di trazione che assicura la
posizione dell’organo mobile.
I nastri hanno anche il compito di fornire la
coppia antagonista e spesso anche di addurre
corrente alla parte mobile.
Non vi sono parti in moto relativo, sicché la
coppia d’attrito è molto piccola, essendo dovuta
solo agli attriti molecolari dei nastri e delle loro
giunzioni. Pertanto si possono impiegare coppie
motrici notevolmente minori di quelle di uno
strumento a perni (100-1000 volte più piccole).
L’equipaggio mobile risulta elastico e capace di
sopportare urti e vibrazioni, purché le sue
escursioni traversali siano limitate da appositi
arresti
Sospensioni a nastro
34
Sospensioni
Strumenti particolari, come ad esempio i contatori, con equipaggio
mobile più pesante, utilizzano delle sospensioni speciali, a perni
cilindrici orizzontali o verticali, in parte scaricati da sospensioni
magnetiche.
Nel caso dei contatori, l’equipaggio mobile deve ruotare in modo
continuo; pertanto, nella parte terminale dell’equipaggio mobile, al
posto della punta del perno vi è una sfera di rotolamento (estremità
dell’equipaggio mobile e parte fissa sono concave e in mezzo vi è la
sfera di rotolamento.
Le azioni magnetiche delle sospensioni stabilizzano l’equipaggio
mobile.
Sospensioni
a filo teso
35
36
9
Scale
Molle
• Generalmente le molle hanno il compito di fornire la coppia
resistente; spesso hanno anche il compito di portare la corrente
all’organo mobile. Al termine della sollecitazione, la molla deve
riportare l’indice a zero, senza apprezzabili effetti di isteresi elastica
o variazione termica.
• Negli strumenti con sospensione a perno le molle sono a spirale
piatta (di bronzo fosforoso), con un estremo collegato al telaio dello
strumento e l’altro estremo fissato al perno dell’equipaggio mobile
• La coppia resistente fornita dalle molle diminuisce al crescere della
loro temperatura; ciò comporta un limite nella corrente che le può
percorrere (alcune decine, al massimo un centinaio di milliampere).
• La corrente che percorre le molle deve essere limitata anche per
evitare un riscaldamento eccessivo, con conseguente deviazione
dell’indice dovuta alla dilatazione termica delle molle; in genere
questo effetto si compensa dall’esterno, mediante la rotazione
dell’estremo collegato al telaio, oppure utilizzando due molle,
avvolte in senso contrario, in modo da compensare gli effetti termici
37
e facilitare l’adduzione di corrente.
Scale
La scala è composta da un
insieme di tratti numerati, sul
quale può essere letta la posizione
di un indice di riferimento.
I requisiti di una scala (forma,
numerazione) dipendono dall’uso
dello strumento.
Ad es. negli apparecchi
industriali, da quadro, la lettura
deve poter essere eseguita
rapidamente, da una certa
distanza; inoltre, per ragioni di
costo, le scale devono avere
lunghezza limitata. Pertanto, sono
tollerabili incertezze di lettura
dell’ordine dell’1%.
38
Scale
Negli strumenti di precisione e di
controllo si tende invece a ridurre
l’incertezza di lettura a valori
dell’ordine di un decimo
dell’indice di classe; ciò comporta
maggiori dimensioni degli
strumenti e maggiore attenzione
richiesta all’operatore.
L’andamento della scala può
essere lineare, quadratico,
contratto (verso l’inizio, verso il
fondo scala, verso entrambi), a
zero centrale, ecc.
La lunghezza della scala è
proporzionale alla massima
distanza di lettura e inversamente
proporzionale all’incertezza di
lettura ammissibile
39
La lunghezza della scala è correlata alla classe dello strumento.
Si dimostra, infatti, che un operatore “medio” può apprezzare la lettura su
una scala con un’incertezza minima dell’ordine di 1/5 dell’intervallo tra due
divisioni. Tale frazione rappresenta quindi l’ultima cifra significativa
leggibile.
Pertanto, per avere un’incertezza di lettura dell’1% è sufficiente dividere la
scala in 20 divisioni.:
Δδ = (1/5) (1/20) = 1/100 = 1% (una divisione è 1/20 del fondo scala)
Se si vuole un’incertezza di lettura inferiore, bisogna aumentare il numero di
divisioni
La scala può essere effettiva (quando il valore letto è direttamente quello
della grandezza misurata) o fittizia. Nel secondo caso la misura si ottiene
moltiplicando la lettura δ0 per la costante strumentale k:
M = δ0 k
k = P / N (P = portata, N = numero di divisioni a fondo scala)
40
10
Errore di parallasse
Tipi di indici
Anche la forma e le dimensioni
dell’indice sono in relazione con
la massima incertezza di lettura
ammissibile e quindi con la classe
di precisione dello strumento.
Tanto più la punta dell’indice è
sottile tanto meglio definita è la
lettura. Essa però risulta più
faticosa al crescere della distanza
Si hanno indici a lancia (per
strumenti da quadro), a lama o a
filo teso (per strumenti di
precisione).
Quando il piano dell’indice non
coincide con quello della scala si
può commettere un errore di
lettura (errore di parallasse)
41
Strumenti con indice ottico
GALVANOMETRO
L’indice metallico può
VETRO SMERIGLIATO
essere sostituito da un
raggio luminoso che,
SCALA
DI
riflesso da uno
specchietto solidale con LETTURA
l’equipaggio mobile,
fornisce su una scala
LENTE
trasparente un’immagine
provvista di un segno di
riferimento.
L’indice ottico ha il
SPECCHIO
vantaggio della
leggerezza e dell’assenza
di parallasse.
Richiede però un dispositivo di
alimentazione della sorgente luminosa.
Per evitare l’errore di parallasse occorre che l’operatore si ponga sulla
verticale dell’indice; ciò può essere verificato disponendo uno specchio
nelle vicinanze della scala e controllando che l’indice si sovrapponga alla
42
sua immagine.
Sistemi di smorzamento
SPECCHIO
GENERATORE
LAMA DI LUCE
43
• Uno strumento indicatore deve assumere rapidamente la
sua posizione di regime, senza oscillazioni di ampiezza
eccessiva intorno ad essa, anche quando la coppia motrice
sia applicata bruscamente.
• A tale scopo si impiegano gli smorzatori, che possono
essere:
– Smorzatori a fluido
– Smorzatori elettromagnetici
44
11
Sistemi di smorzamento
Sistemi di smorzamento
• Smorzatori elettromagnetici
– con campo magnetico proprio
lo smorzamento è assicurato da una
bobina (che può anche essere la stessa che
fornisce la coppia motrice); nel suo moto
nel campo magnetico sulla bobina si
induce una f.e.m. proporzionale alla
velocità di rotazione; la corrente che ne
risulta si oppone al moto che l’ha
provocata.
• Smorzatori a fluido
– Negli smorzatori ad aria un pistone (o
una ventola) si muove in un condotto
chiuso, forzando l’aria ad uscire nello
spazio fra il pistone e le pareti del
contenitore, dissipando energia per
attrito
– Gli smorzatori a liquido (acqua, olio
di glicerina) possono fornire coppie di
smorzamento maggiori ma presentano
maggiore inerzia ed una marcata
variabilità del coefficiente di
smorzamento con la temperatura.
45
Sistemi di smorzamento
46
Contrassegni
Oltre alla numerazione della scala, ogni strumento porta un certo numero di
indicazioni e di simboli, che ne individuano le caratteristiche e le
prestazioni. Le indicazioni più frequenti sono le seguenti:
• Numero di matricola dello strumento (serve a riconoscere l’apparecchio,
i suoi eventuali accessori, la sua tabella di taratura ecc.)
• Nome del costruttore e marchio (che indica secondo quali norme è stato
costruito lo strumento)
• Grandezza misurata ed eventuale costante di lettura
• Indice della classe di precisione
• Tipo di strumento, indicato da un segno grafico convenzionale (vedi
appresso)
• Tipo di circuito a cui lo strumento può essere connesso (corrente
continua, alternata, monofase, trifase, ecc., con eventuale campo di
frequenze di impiego)
• Posizione prevista per il quadrante (verticale, orizzontale, inclinata)
• Tensione di prova (in kV, indicata con un numero in una stella)
con campo magnetico esterno
si utilizza un magnete permanente; la
parte mobile, ha la forma di una lamina o
disco conduttore; essa, muovendosi fra le
espansioni polari del magnete, è sede di
una circolazione di corrente che
determina la nascita di una coppia
smorzante.
47
48
12
Contrassegni
Simboli strumenti elettromeccanici
Oltre alle precedenti indicazioni, sugli strumenti portatili o a portate
multiple, i singoli morsetti e le varie posizioni dei commutatori hanno
le opportune indicazioni.
I morsetti amperometrici, destinati ad essere collegati in serie al
circuito, si distinguono in genere per la loro maggiore sezione rispetto a
quelli voltmetrici.
49
Simboli strumenti elettromeccanici
50
Simboli strumenti elettromeccanici
51
52
13
Modalità di visualizzazione in uno strumento di
misura elettromeccanico
Modalità di visualizzazione in uno strumento di
misura elettromeccanico
• Portata o range: il più grande dei valori del campo di
misura. Uno strumento ha normalmente più portate.
• Fondo scala (FS): Il numero più grande dei valori indicati
sulla scala.
• Costante strumentale (Ks): è il rapporto tra la portata ed
il fondo scala. Nella strumentazione elettromeccanica a più
portate sulla scala sono in genere indicate delle divisioni. Il
numero di divisioni lette (Ndivisioni) va moltiplicato per la
costante strumentale per ottenere la grandezza misurata. Si
ottiene quindi:
M=KsNdivisioni
Portata = 1mA
Portata = 10mA
Fondo scala= 100
Fondo scala= 100
Lettura = 65 divisioni
Lettura = 65 divisioni
Ks= 1/100 mA
Ks= 10/100 mA
Misura = 65/100 mA=0,65 mA Misura = 65/10 mA=6,5 mA
53
Risoluzione e sensibilità
nella strumentazione elettromeccanica
54
Risoluzione e sensibilità
nella strumentazione elettromeccanica
La sensibilità per uno strumento
elettromeccanico è data dal
rapporto fra una variazione Δx
della grandezza misurata e la
corrispondente variazione Δδ
della deviazione dello strumento.
Quando la sensibilità è costante
per ogni valore della grandezza
misurata si ottiene uno strumento
a scala lineare, come in figura b)
e c); nel caso di figura a) lo
strumento ha una sensibilità
aumentata nella regione centrale.
55
La sensibilità non deve essere
confusa con la risoluzione.
La risoluzione per uno strumento
elettromeccanico è la più piccola
variazione della grandezza da
misurare che lo strumento può
indicare con sicurezza (in una
determinata portata).
Le figure b) e c) mostrano come,
a parità di sensibilità, si possano
avere scale con differente
risoluzione.
(Invece, per uno strumento numerico, risoluzione e
sensibilità corrispondono al valore dell’ultima cifra
significativa indicata dallo strumento)
56
14
Comportamento dinamico dell’equipaggio mobile
di uno strumento elettromeccanico
• La posizione angolare δ di un equipaggio mobile, libero di ruotare
attorno al suo asse, è data, istante per istante, dall’equilibrio delle
coppie agenti su di esso:
– coppia motrice Cm, funzione del tempo e legata al misurando x
– coppia elastica di richiamo, che si suppone proporzionale
all’angolo di rotazione δ secondo la costante elastica KM
– coppia di attrito viscoso, che si suppone proporzionale alla
velocità di rotazione dell’equipaggio, secondo un coefficiente
KV (si trascurano le altre coppie di attrito)
– coppia di inerzia, legata alla presenza del momento di inerzia J
dell’equipaggio mobile rispetto al suo asse di rotazione
Comportamento dinamico dell’equipaggio mobile
di uno strumento elettromeccanico
• La posizione istantanea dell’equipaggio mobile si ricava dalla
soluzione della seguente equazione:
J
d 2δ
dδ
+ KV + KMδ = Cm
2
dt
dt
J = momento di inerzia
KV = coefficiente di smorzamento viscoso
KM = costante elastica della molla di richiamo
Cm = coppia motrice
57
• Si definiscono :
1
G=
Fattore di conversione in regime continuo
KM
ζ=
KV
2 KM J
ωn =
KM
J
Fattore di smorzamento
Pulsazione caratteristica
In particolare:
La pulsazione caratteristica individua la scala dei tempi in cui si
sviluppa la risposta del sistema
Il fattore di smorzamento determina la forma della risposta del
59
sistema.
Comportamento dinamico dell’equipaggio mobile di uno
strumento elettromeccanico - Risposta al gradino
Per ζ<1 si ha un andamento sottosmorzato: la risposta è caratterizzata
da una sovraelongazione, tanto maggiore quanto minore è ζ; il
periodo delle oscillazioni decresce al decrescere di ζ; il valore finale
è raggiunto (per t→∝) attraverso una serie di oscillazioni smorzate;
per ζ=0 lo smorzamento è nullo e si ha un andamento periodico della
risposta.
ζ=0.3
ζ=0.6
ζ=1
ζ=3
ζ=0.7
posizione δ
Comportamento dinamico dell’equipaggio mobile
di uno strumento elettromeccanico
58
tempo
ζt
60
15
Comportamento dinamico dell’equipaggio mobile di uno
strumento elettromeccanico - Risposta al gradino
Per ζ>1 si ha un andamento sovrasmorzato: la risposta è di tipo
aperiodico e tende asintoticamente al valore finale; all’aumentare di
ζ, le curve di abbassano e tendono al valore di regime sempre più
lentamente.
Per ζ=1 si ha lo smorzamento critico: la risposta è di tipo aperiodico
ed è quella che raggiunge più rapidamente il valore di regime .
posizione δ
ζ=0.3
ζ=0.6
ζ=1
ζ=3
ζ=0.7
Comportamento dinamico dell’equipaggio mobile
di uno strumento elettromeccanico - Risposta al gradino
sovraelongazione (differenza fra il valore massimo e il valore finale)
fascia di incertezza
specificata
ζ=0.3
ζ=0.7
tempo di salita
tempo di risposta
tempo di assestamento
ζt
tempo
61
Risposta armonica o in frequenza
Il Segnale è:
t
62
Risposta in frequenza ad una singola sinusoide
V
Amplificato e sfasato
Dato un ingresso sinusoidale, del tipo
x(t) = Cm sen(nωt + ϕn)
la risposta del sistema, nel dominio del tempo è data da::
ym = g (nω ) Cm sen(nωt + ϕ m + ϕT (nω ))
V
V
(intervallo di tempo necessario affinché il valore
cresca da 0,1 v.f. a 0,9 v.f. )
(intervallo di tempo affinché si raggiunga il valore
massimo)
(istante dopo il quale il valore si mantiene entro la
fascia di incertezza)
ϕT(nω) è lo sfasamento introdotto dalla funzione di trasferimento.
Sistema
del II ordine
t
ζ
ωn =
t
La risposta ad un segnale di ingresso sinusoidale di pulsazione ω è
determinabile attraverso la funzione di trasferimento particolarizzata nella
sua parte complessa:
Inalterato
V
V
t
Ridotto e sfasato
Annullato
t
63
g ( jω ) =
G
jω ⎛ ω
1 + 2ζ
+ ⎜⎜
ωn
⎝ ωn
⎞
⎟⎟
⎠
2
64
16
Comportamento dinamico dell’equipaggio mobile
di uno strumento elettromeccanico – Funzione di
Trasferimento (FDT) - Risposta in frequenza
g ( jω ) =
Risposta in frequenza – Andamento del modulo della FDT
g(ω )
5
G
jω ⎛ ω
1 + 2ζ
+ ⎜⎜
ωn
⎝ ωn
⎞
⎟⎟
⎠
La pulsazione caratteristica ωn individua la scala dei
tempi in cui si sviluppa la risposta del sistema
Il fattore di smorzamento ζ determina la forma della
risposta del sistema.
Dividendo la FDT per G, si ottiene la FDT ridotta, di
cui si riportano gli andamenti seguenti.
4
2
3
1
G=
KM
ζ=
2
KV
2 KM J
ωn =
KM
J
65
Risposta in frequenza – Andamento del modulo della FDT
Per ζ < 1, la FDT ha un
massimo maggiore di 1; al
limite, per ζ = 0, la curva a
campana avrebbe lati
asintoticamente tendenti a
ω/ωn = 1.
I massimi della FDT (punti di
risonanza) si verificano per
frequenze più basse al
crescere di ζ.
g(ω )
ζ = 0.1
3
2
0.5
1
0.7
1
2
0.5
0.5
1
0.7
1
2
0.5
1
1.5
2
La curva corrispondente a ζ = 0,7 è quella che più delle altre si
approssima all’unità in una data banda di frequenza.
Il fatto che le curve per ζ < 1 presentino un massimo significa che, per
opportuni valori di frequenza è possibile ottenere un’amplificazione
67
della grandezza in ingresso.
ω
ωn
1
1.5
2
ω
ωn
66
Risposta in frequenza – Andamento del modulo della FDT
Per ζ ≥ 1, le curve del
modulo della FDT partono da
1 e si abbassano al crescere
della frequenza.
In questo caso si ha
un’attenuazione del segnale
in ingresso.
Per ζ = 1, si ha la risposta
critica.
5
4
ζ = 0.1
g(ω )
5
4
ζ = 0.1
3
2
0.5
1
0.7
1
2
0.5
1
1.5
ω
ωn
2
68
17
Risposta in frequenza –Andamento della fase della FDT
L’andamento della fase
nell’intorno di ζ = 0,7, nel
campo di frequenze che
vanno dalla corrente continua
fino alla pulsazione di
risonanza ω/ωn = 1, è
pressoché lineare. In questo
campo di frequenze le fasi
sono negative; ciò vuol dire
che la grandezza in uscita allo
strumento è in ritardo rispetto
al segnale in ingresso.
(cioè, in un sistema fisico la
risposta segue l’ingresso)
ϕ
ζ = 0.1
- 30
- 60
2
0.5
0.7
1
- 90
-120
-150
-180
0.5
1
1.5
2
Risposta in frequenza –Andamento della fase della FDT
ω
ωn
ϕ
ζ = 0.1
- 30
0.5
0.7
- 60
2
1
- 90
-120
-150
-180
0.5
1
1.5
ω
ωn
2
69
70
Requisiti dinamici di uno strumento indicatore
Requisiti dinamici di uno strumento indicatore
• Uno strumento indicatore deve assumere rapidamente la sua
posizione di regime, senza oscillazioni eccessive intorno ad
essa, anche quando la coppia motrice sia applicata bruscamente
(al limite, ingresso a gradino)
• Dall’andamento della risposta al gradino, si è visto che per un
sistema del secondo ordine si hanno delle condizioni di
smorzamento che consentono di raggiungere la situazione di
regime senza oscillazioni o in un tempo minimo.
• Le norme tuttavia ammettono che l’indice compia una
sovraelongazione e che abbia un moto oscillatorio; questo
perché in questo modo si può verificare se l’indice sia libero di
muoversi o se risulta frenato da qualche causa accidentale
Le norme ammettono che l’indice compia
una sovraelongazione non superiore al 30%
del valore finale e che compia un moto
oscillatorio la cui ampiezza sia non superiore
allo 0,75% del valore finale dopo 4 secondi
71
72
18
Rilievo di grandezze periodiche – Strumenti registratori
Requisiti dinamici di uno strumento indicatore
• Negli strumenti registratori si richiede una riproduzione
fedele del segnale in ingresso.
• Dalla sovraelongazione, 30% del valore di regime, e dalla
riduzione dell’ampiezza dell’oscillazione a non più del 75%
dopo 4 s si ricavano:
• Per determinare la banda di frequenza in cui il sistema non
deforma il segnale ad esso applicato, occorre conoscere
quale sia il valore massimo della pulsazione ω per cui un
segnale sinusoidale d’entrata viene trasferito all’uscita senza
mutare ampiezza e fase.
• Questo valore limite si ricava imponendo per la g(ω) un
certo scarto massimo Δ ammissibile rispetto al valore
unitario; per Δ = 1% si ottiene ζ = 0,65, ω = 0,6 ωn
– Il fattore di smorzamento dell’equipaggio mobile (non
inferiore a 0,38)
– La pulsazione naturale dell’equipaggio mobile (non
inferiore a 3,5 rad/s)
73
74
Segnali periodici – Teorema di Fourier
• Il segnale di ingresso può essere scomposto in serie di Fourier.
Teorema di Fourier
∞
f ( t ) = A 0 + ∑ C n sin (nωt + ϕn )
n = 1,2, L , ∞
n =1
f ( t ) periodica nel tempo con frequenza f = 1 T = ω 2π
Se si pone :
A n = C n sinϕn
Risulta :
75
Bn = C n cos ϕn
C n = A 2n + B2n
ϕn = arctg(A n Bn )
76
19
Rilievo di grandezze periodiche – Strumenti registratori
La risposta in frequenza o armonica per un segnale periodico è la
seguente:
y(t)=GA0+∑n=1÷∞|g(nω)|Cnsen(nωt+ϕn + ϕT(nω) )
• La y(t) è data dalla funzione di ingresso amplificata di G e traslata
temporalmente di ϕT(nω)
• Per il trasferimento indistorto di un segnale periodico,
scomponibile in serie di Fourier, occorre che le singole armoniche
siano trasmesse inalterate in ampiezza e siano tutte ritardate dello
stesso intervallo di tempo; ciò equivale ad imporre che la fase
della funzione di trasferimento vari linearmente con la pulsazione.
• Questa condizione imporrebbe uno smorzamento pari a circa
0,75-0,80; tuttavia adottando i valori precedentemente ottenuti (ζ
= 0,65, ω = 0,6 ωn) la distorsione rimane contenuta entro qualche
centiradiante.
Sistemi selettivi
• La caratteristica del secondo ordine di un equipaggio mobile
consente la realizzazione di strumenti selettivi, senza
l’interposizione di filtri.
• Un’applicazione è quella dei rivelatori di zero in corrente
alternata, ove si vuole rilevare l’azzerarsi di un segnale elettrico
ad una data frequenza, anche quando il segnale contenga altre
componenti a frequenza diversa da quella di interesse.
• Uno strumento selettivo si realizza scegliendo opportunamente il
coefficiente di smorzamento: in questo caso occorre far lavorare
lo strumento in condizioni vicine alla risonanza, con valori di ζ
bassi, in modo tale da avere una banda passante stretta. In questo
modo lo strumento si comporta come un filtro, “accordato” alla
frequenza di interesse.
77
Sistemi selettivi
• Per esempio, per ζ = 0,1
lo strumento amplificherà
al massimo la
componente del segnale
con pulsazione pari a
quella caratteristica,
mentre tutte le altre
armoniche saranno
fortemente attenuate.
Classificazione strumenti elettromeccanici
• Esistono diversi tipi di strumenti elettromeccanici in dipendenza del
principio di funzionamento e quindi del legame esistente tra la coppia
motrice e la grandezza di ingresso.
• Fondamentalmente si possono distinguere strumenti basati su sistemi:
– elettromagnetici (interazione fra una corrente e un campo
magnetico)
g(ω )
5
4
ζ = 0.1
3
• Possono misurare grandezze cc (a bobina mobile) o cc e ac (a ferro
mobile)
2
0.5
1
– elettrostatici, (interazione fra conduttori in tensione)
0.7
1
• Possono misurare grandezze cc e ac
2
0.5
78
1
1.5
ω
ωn
2
– elettrodinamici (interazione fra correnti)
• Possono misurare grandezze cc e ac
• In conclusione, in base al segnale che si vuole analizzare, si
sceglie lo strumento che abbia adeguata banda passante, in
modo da far “passare” solo la componente del segnale alla
frequenza di interesse, attenuando tutte le altre componenti
– a induzione (interazione fra correnti indotte in un disco di
materiale conduttore)
– • Possono misurare solo grandezze ac
79
– termici (effetto Joule).
80
20
Classificazione strumenti elettromeccanici
• Si distinguono quindi in base al legame tra la coppia motrice e
la grandezza elettrica in ingresso da misurare che può essere di
tipo:
– Proporzionale;
– Quadratico e quasi quadratico;
– A prodotto o a quoziente.
81
21