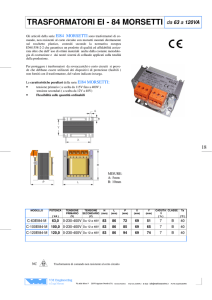
Conversione Elettromeccanica
Esercizio 4.
A.A. 2002/2003
PARALLELO DI DUE TRASFORMATORI MONOFASE DI
DIVERSA POTENZA (dalla prova di recupero dell’a.a. 2001/02)
Due trasformatori monofase, funzionanti a 50 Hz, sono collegati in parallelo per alimentare un
carico induttivo, con fattore di potenza cosϕcarico = 0,8, da una sorgente a V1n = 3000 V.
La tensione sul carico sia pari a VC = 230 V.
I dati dei due trasformatori sono riportati nella tabella seguente:
DATI
Trasformatore A
Trasformatore B
Tensione primaria nominale
V1n = 3000 V
V1n = 3000 V
Tensione secondaria nominale
V2n = 240 V
V2n = 240 V
Potenza apparente nominale
AnA = 30 kVA
AnB = 90 kVA
Tensione di corto circuito
V2ccA = 10,8 V
V2ccB = 12 V
Potenza attiva assorbita in corto circuito PccA = 750 W
PccB = 1350 W
Corrente misurata in corto circuito
I2nB
I2nA
Si determinino:
a)
le correnti nominali primarie e secondarie I1nA, I2nA, I1nB, I2nB;
b) le impedenze di corto circuito riferite ai secondari Z2ccA , Z2ccB in modulo e fase;
c) l’impedenza equivalente del parallelo dei due trasformatori Zeq in modulo e fase;
d) la corrente di carico IC in modulo e fase, fissando la fase della tensione sul carico (VC = 0° e
ipotizzando che il valore della fase della tensione secondaria V2n sia molto piccolo;
e) la potenza complessiva fornita dai due trasformatori A C ;
f)
la potenza fornita da ciascuno dei due trasformatori, verificando se in queste condizioni i due
trasformatori sono o non sono in sovraccarico.
N.B.: Per lo svolgimento dei calcoli, si consideri come riferimento una rete equivalente semplificata
riferita ai secondari, come quella illustrata in figura.
Esercizio 4 sui trasformatori
Pag. 1 di 4
Conversione Elettromeccanica
A.A. 2002/2003
Soluzione dell’Esercizio 4
a)
I1nA =
A nA 30000
=
= 10 A
V1n
3000
I1nB =
A nB 90000
=
= 30 A
V1n
3000
I 2nA =
A nA 30000
=
= 125 A
V2n
240
I 2nB =
A nB 90000
=
= 375 A
V2n
240
b) Nelle prove di corto circuito sono stati cortocircuitati i terminali del primario e le grandezze
misurate si riferiscono al secondario, perciò possiamo calcolare direttamente le impedenze di
corto circuito riferite ai secondari Z2ccA e Z2ccB .
I moduli delle impedenze di corto circuito riferite ai secondari sono:
Z2ccA =
V2ccA 10,8
=
≅ 0, 086 Ω
I 2nA
125
Z2ccB =
V2ccB 12
=
≅ 0, 032 Ω
I 2nB 375
Le resistenze di corto circuito riferite ai secondari sono:
R 2ccA =
PccA
I 22nA
=
750
125
2
≅ 0, 048 Ω
R 2ccB =
PccB
I 22nB
=
1350
3752
≅ 0, 010 Ω
Le reattanze di corto circuito riferite ai secondari sono:
X 2ccA = Z22ccA − R 22ccA = 0, 072 Ω
X 2ccB = Z22ccB − R 22ccB = 0, 031Ω
Le fasi delle impedenze di corto circuito sono:
X
ϕccA = arctan 2ccA ≅ 56,3°
R 2ccA
Esercizio 4 sui trasformatori
X
ϕccB = arctan 2ccB ≅ 72,5°
R 2ccB
Pag. 2 di 4
Conversione Elettromeccanica
A.A. 2002/2003
Quindi, le impedenze di corto circuito riferite ai secondari espresse in modulo e fase sono:
Z2ccA = 0, 086∠56,3°Ω
Z2ccB = 0, 032∠72,5°Ω
c) L’impedenza equivalente del parallelo dei due trasformatori Zeq è data da:
Zeq =
Z2ccA ⋅ Z2ccB ( ( Z2ccA ⋅ Z2ccB )
Z2ccA ⋅ Z2ccB
0, 003∠128,8° 0, 003∠128,8°
=
≅
≅
Z2ccA +Z2ccB ( R 2ccA +R 2ccB ) + j ( X 2ccA +X 2ccB ) 0,058 + j0,102 0,117∠60, 6°
⇒ Zeq ≅ 0, 024∠68, 2° Ω
⇒
Zeq ≅ 0, 009 + j0, 022 Ω
d) Per calcolare la corrente di carico IC , facciamo riferimento al seguente circuito equivalente:
In questo circuito equivalente ogni grandezza è vettoriale e perciò rappresentata tramite un
modulo e una fase. Di queste grandezze conosciamo:
•
V2n in modulo: V2n = 240 V ;
•
Zeq in modulo e fase: Zeq = 0, 024∠68, 2° Ω ;
•
la fase tra IC e VC : sappiamo infatti che il carico è induttivo con cosϕcarico = 0,8 , quindi
ϕcarico ≅ −36,9° , che rappresenta la fase di IC , una volta fissata (VC = 0° ;
•
VC in modulo e fase: VC = 230∠0° V .
Rimangono quindi due incognite: il modulo di IC e la fase di V2n , che chiamiamo ϕ .
Possiamo scrivere l’equazione alla maglia del circuito equivalente:
V2n − Zeq IC = VC
⇒
240∠ϕ − 0, 024 ⋅ IC∠ ( 68, 2° − 36,9° ) = 230∠0°
⇒ 240∠ϕ − 0, 024 ⋅ IC∠31,3° = 230∠0°
Questa è un’equazione vettoriale che può essere scomposta in due equazioni scalari e pertanto
essere risolta nelle due incognite ϕ e IC :
240 cos ϕ − 0, 024 ⋅ IC cos 31,3° = 230
240sin ϕ − 0, 024 ⋅ IC sin 31,3° = 0
Esercizio 4 sui trasformatori
Pag. 3 di 4
Conversione Elettromeccanica
A.A. 2002/2003
Ipotizzando che ϕ sia molto piccolo: ⇒
cos ϕ ≅ 1
sin ϕ ≅ ϕ
240 − 0, 024 ⋅ IC cos 31,3° = 230
⇒
240ϕ − 0, 024 ⋅ IC sin 31,3° = 0
Dalla prima equazione ricaviamo IC :
⇒ IC =
240 − 230
≅ 497 A
0, 024 ⋅ cos 31,3°
Dalla seconda equazione ricaviamo ϕ :
⇒ ϕ=
0, 024 ⋅ 497 ⋅ sin 31,3°
≅ 1,5°
240
⇒
l’ipotesi di ϕ molto piccolo è verificata.
e) La potenza complessiva fornita dai due trasformatori A C è data da:
A C = IC ⋅ VC = 497 ⋅ 230 ≅ 114343VA ≅ 114 kVA
f)
Per calcolare la potenza fornita da ciascuno dei due trasformatori, calcoliamo prima la corrente
fornita da ciascuno dei due trasformatori:
I2A =
I2B =
Zeq ⋅ IC
Z2ccA
Zeq ⋅ IC
Z2ccB
=
0, 024 ⋅ 497∠ ( 68, 2° − 36,9° )
≅ 135∠ − 25° A
0, 086∠56,3°
=
0, 024 ⋅ 497∠ ( 68, 2° − 36,9° )
≅ 366∠ − 41,3° A
0, 032∠72,5°
La potenza fornita da ciascuno dei due trasformatori è data da:
A A = VC ⋅ I 2A = 230 ⋅135 ≅ 31 kVA
A B = VC ⋅ I 2B = 230 ⋅ 366 ≅ 84 kVA
Il grado di carico di ciascuno dei due trasformatori è:
αA =
I 2A 135
=
≅ 108%
I 2An 125
αB =
I 2B 366
=
≅ 98%
I 2Bn 375
Esercizio 4 sui trasformatori
⇒
il trasformatore A è sovraccaricato
Pag. 4 di 4